Потоки в сетях. Задача о максимальном потоке

1.

ПОТОКИ В СЕТЯХ
Задача о максимальном потоке
Сеть – это ориентированный граф
G (V , E) ,
каждому ребру
c(vi , v j ) 0 ,
называемое пропускной способностью, а также выделено две вершины v0 исток и vn 1 - сток, n V .
Поток – это функция f (vi , v j ) , (vi , v j ) E обладающая тремя
(vi , v j )
которого поставлено в соответствие число
свойствами:
1. f (vi , v j ) c(vi , v j ) ;
2.
3.
f (vi , v j ) f (v j , vi ) (кососимметричность);
f (u, v) 0 , u V {v0 , vn 1}
v V

2.

Величина потока
Примем
f
vi V , f
это
f
f (v0 , v j )
v V
(vi , v j ) 0 ,
f (v j , vi ) 0
f (vi , v j ) - величина входящего потока для вершины
vi V
vj
f (vi , v j ) - величина исходящего потока для вершины
v j V
vi

3.

12
1
2
16
20
10
0
5
9
4
7
13
4
4
3
14
12
1
2
11
15
0
5
4
1
7
8
4
4
f
11
f (v0 , v j ) 11 8 19
v V
3

4.

( S , T ) сети G (V , E) называется разбиение множества V
на две части S и T такое, что
v0 S , vn 1 T , S T V ,
S T .
Пропускная способность разреза c( S , T ) – это сумма пропускных
способностей дуг соединяющих вершины в S и T .
Разрез
Минимальный разрез сети – это разрез с минимальной пропускной
способностью.

5.

12
1
2
16
20
10
0
5
9
4
7
13
4
4
14
3
({0,1,4}, {2,3,5}) ,
c({0,1,4}, {2,3,5}) c(1,2) c(4,3) 12 14 26
Разрез

6.

12
1
2
11
15
0
5
4
1
7
8
4
4
11
3
({0,1,4}, {2,3,5})
f (1,2) f (4,3) f (2,4) 12 11 ( 4) 19
Поток через разрез

7.

Теорема Форда-Фалкерсона: В любой сети максимальная величина
потока из истока s в сток t равна минимальной пропускной
способности разреза отделяющего s от t .
12
1
2
16
20
10
0
5
9
4
7
13
4
4
14
3

8.

12
1
2
16
20
10
0
5
9
4
7
13
4
4
3
14
29
12
1
2
16
20
10
0
5
9
4
7
13
4
4
35
14
{0,1}
3

9.

12
1
2
16
20
10
0
5
9
4
7
13
4
4
58
14
3
{0,2}
12
1
2
16
20
10
0
5
9
4
7
13
4
4
52
14
{0,1,2}
3

10.

12
1
2
16
20
10
0
5
9
4
7
13
4
4
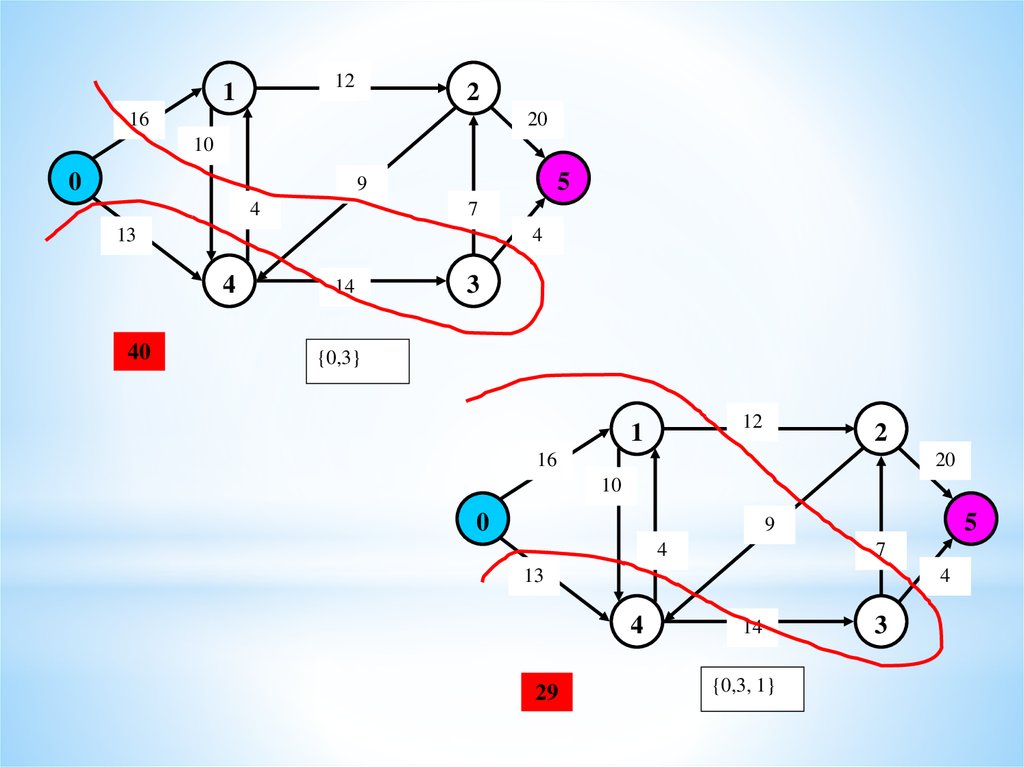
40
14
3
{0,3}
12
1
2
16
20
10
0
5
9
4
7
13
4
4
29
14
{0,3, 1}
3

11.

12
1
2
16
20
10
0
5
9
4
7
13
4
4
53
14
3
{0,3, 2}
12
1
2
16
20
10
0
5
9
4
7
13
4
4
46
14
{0,3, 2, 1}
3

12.

12
1
2
16
20
10
0
5
9
4
7
13
4
4
34
14
3
{0,4}
12
1
2
16
20
10
0
5
9
4
7
13
4
4
26
14
{0,1,4}
3

13.

12
1
2
16
20
10
2
16
0
5
9
4
0
4
4
4
4
12
3
14
{0,3,4}
27
1
7
13
{0,2,4}
4
0
5
9
4
3
14
20
10
7
13
2
16
20
10
12
1
0
5
9
4
14
3
20
10
4
4
2
16
7
13
34
12
1
0
5
9
4
7
13
{0,1, 2,4}
4
4
23
14
{0,1, 3,4}
3

14.

12
1
2
16
20
10
0
5
9
4
7
13
4
4
40
3
14
{0,2, 3,4}
12
1
2
16
20
10
0
5
9
4
7
13
4
4
24
14
{01,,2, 3,4}
3

15.

16
20
5
0
13
4
+
+
10
S
1
+
T
15
11
22
+
3
6
20
7

16.

Понятие остаточной сети
Сеть
G (V , E) , c(vi , v j ) - пропускная способность дуги
12
1
2
16
20
10
0
5
9
4
7
13
4
4
Поток
3
14
f (vi , v j )
12
1
2
11
15
0
5
4
1
7
8
4
4
11
3

17.

АЛГОРИТМ ФОРДА-ФАЛКЕРСОНА
1. Обнуляем все потоки. Остаточная сеть изначально совпадает с
исходной сетью.
2. В остаточной сети находим любой путь из источника в сток. Если
такого пути нет, останавливаемся.
3. Пускаем через найденный путь (он называется увеличивающим
путём или увеличивающей цепью) максимально возможный поток:
На найденном пути в остаточной сети ищем ребро с
минимальной пропускной способностью cmin.
Для каждого ребра на найденном пути увеличиваем поток на
cmin, а в противоположном ему - уменьшаем на cmin.
Модифицируем остаточную сеть. Для всех рёбер на найденном
пути, а также для противоположных им рёбер, вычисляем новую
пропускную способность. Если она стала ненулевой, добавляем ребро к
остаточной сети, а если обнулилась, стираем его.
4. Возвращаемся на шаг 2.

18.

12
1
2
16
20
10
0
5
9
4
7
13
4
4
0
1
2
3
4
5
0
0
-4
0
0
0
0
3
14
1
4
0
-4
0
0
0
2
0
4
0
0
-4
0
3
0
0
0
0
4
-4
4
0
0
4
-4
0
0
5
0
0
0
4
0
0

19.

4
4
8
1
12
2
20
4
10
0
5
5
4
7
13
4
4
3
10
4
0
1
2
3
4
5
0
0
-11
0
0
0
0
1
11
0
-4
0
-7
0
2
0
4
0
7
-4
--7
3
0
0
-7
0
11
-4
4
0
7
4
-11
0
0
5
0
0
7
4
0
0

20.

4
11
8
1
5
13
4
3
7
2
0
5
11
5
7
13
4
4
3
3
11
0
1
2
3
4
5
0
0
-11
0
0
-8
0
1
11
0
-12
0
1
0
2
0
12
0
7
-4
-15
3
0
0
-7
0
11
-4
4
8
-1
4
-11
0
0
5
0
0
15
4
0
0

21.

-12
11
1
15
2
5
5
4
11
0
5
5
7
3
5
4
4
8
3
3
11
0
1
2
3
4
5
0
0
-11
0
0
-12
0
1
11
0
-12
0
1
0
2
0
12
0
7
-0
-19
3
0
0
-7
0
11
-4
4
12
-1
0
-11
0
0
5
0
0
19
4
0
0

22.

-12
11
1
19
2
5
1
11
0
5
9
7
3
1
4
4
12
3
3
11
0
1
2
3
4
5
0
0
-11
0
0
-12
0
1
11
0
-12
0
1
0
2
0
12
0
7
-0
-19
3
0
0
-7
0
11
-4
4
12
-1
0
-11
0
0
5
0
0
19
4
0
0

23.

0
0
-11
0
0
-12
0
0
1
2
3
4
5
1
11
0
-12
0
1
0
1
2
0
12
0
7
-0
-19
3
0
0
-7
0
11
-4
12
4
12
-1
0
-11
0
0
2
11
0
5
0
0
19
4
0
0
19
5
1
7
12
4
4
11
3