Похожие презентации:
Множества и отношения
1. Множества и отношения
МНОЖЕСТВАИ
ОТНОШЕНИЯ
Якимчук Любовь Григорьевна
Преподаватель Технического колледжа
2.
Множество-
это
соединение,
совокупность, собрание некоторых
предметов, объединённых по какомулибо признаку.
Например:
множест во ст удент ов группы;
множест во целых чисел;
множест во т очек на прямой;
множест во книг на полке
3.
Множество,которое не содержит
ни одного элемента, называют
пустым и обозначают Ø
Обозначения: А,В,С,Д - множест ва,
αЄА
(элемент α принадлежит множест ву А);
{1,2,3} (элемент 4 не принадлежит
4
множест ву).
4. ОПЕРАЦИИ НАД МНОЖЕСТВАМИ
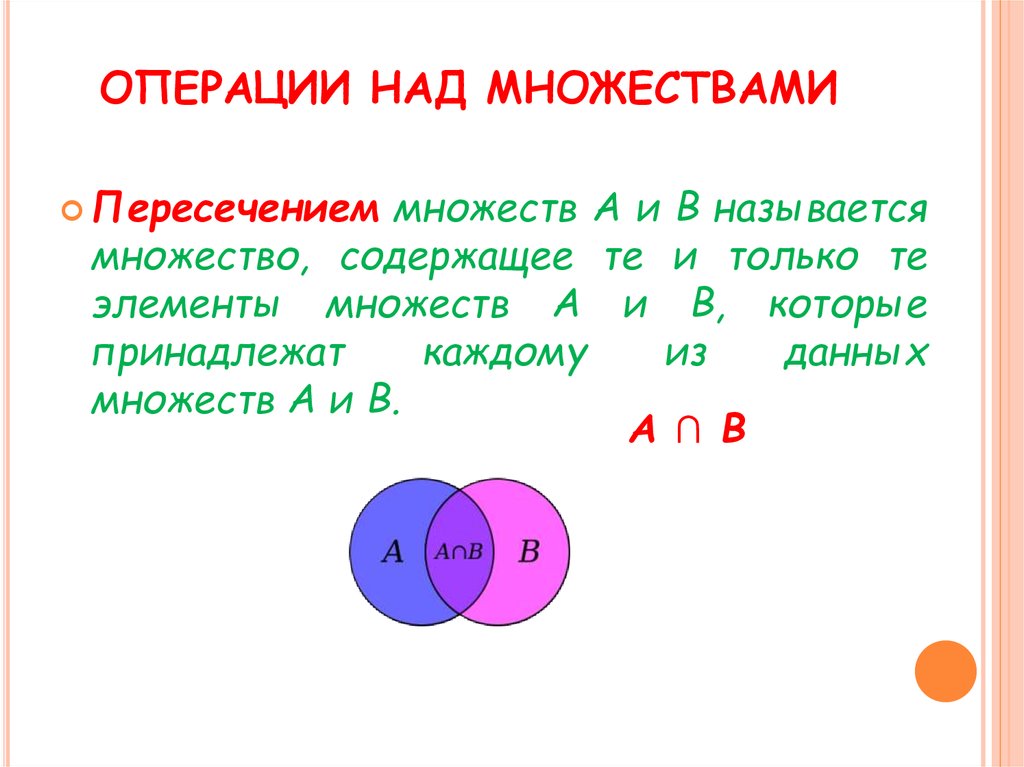
Пересечениеммножеств А и В называется
множество, содержащее те и только те
элементы множеств А и В, которые
принадлежат
каждому
из
данных
множеств А и В.
А ∩ В
5. Пересечение множеств
.ПЕРЕСЕЧЕНИЕ
МНОЖЕСТВ
Свойства:
коммуникативность А ∩В=В ∩А;
ассоциативность
(А∩В) ∩С=А∩(В ∩С);
если В ⊂А, то А ∩В=В и В ∩В=В;
А ∩ Ø =Ø
6. ОПЕРАЦИИ НАД МНОЖЕСТВАМИ
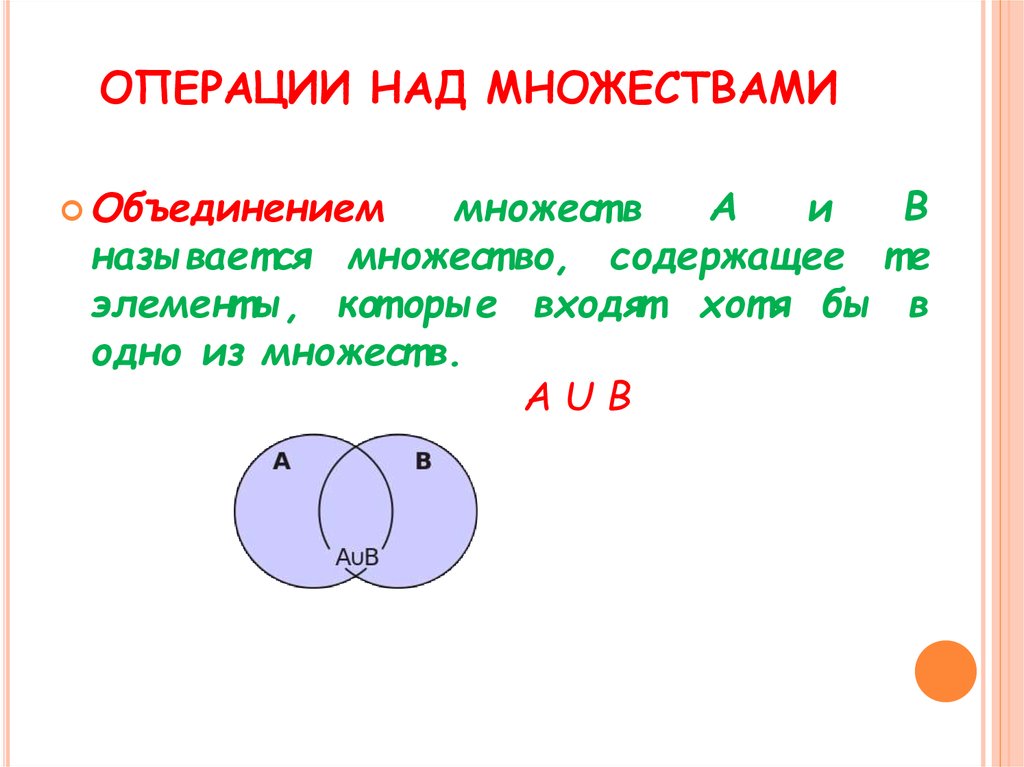
Объединениеммножест в
А
и
В
называет ся множест во, содержащее т е
элемент ы, кот орые входят хот я бы в
одно из множест в.
АUВ
7. Объединение множеств
.ОБЪЕДИНЕНИЕ
МНОЖЕСТВ
Свойст ва:
• АUВ=ВUА;
• АU(ВUС)=(АUВ)UС;
• Если В ⊂А, ВUА=А и АUА=А;
• АUØ=А
8. ОПЕРАЦИИ НАД МНОЖЕСТВАМИ
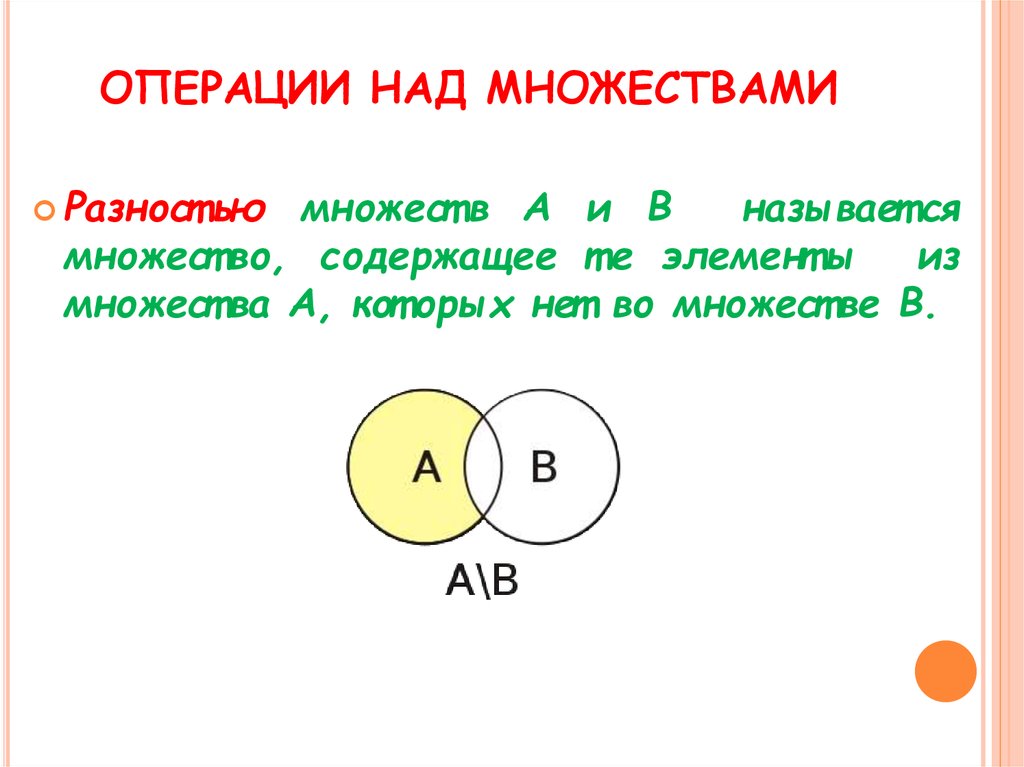
Разностью множест в А и В
называет ся
множест во, содержащее т е элемент ы из
множест ва А, кот орых нет во множест ве В.
9. ОПЕРАЦИИ НАД МНОЖЕСТВАМИ
Декартовым произведением множест в А и В
называет ся множест во пар вида (а; в), где
а Є А и в Є В.
АхВ={(а;b)| а Є А,b Є В}
10. ОТНОШЕНИЯ
Отношение – эт о некот орое подмножест во
пар декарт ова произведения множест в А и
В, т .е. С=А×В.
Обозначает ся:
a R b (элемент а находит ся в от ношении с элемент ом b).
11. СВОЙСТВА ОТНОШЕНИЙ
• рефлексивност ь:если а ϵ А , т о а R a;
• симмет ричност ь:
если а, b ϵ А и
а R b, т о
b R a;
• транзит ивност ь:
если а, b, с ϵ А, а R b и с R b, т о а R с.
Если от ношение R обладает свойст вами 1-3,
то оно называет ся от ношением эквивалент ност и.
12. ВИДЫ ОТНОШЕНИЙ
От ношения между элемент ами множест ва:
От ношения между числами (=; >; <; ≤; ≥);
От ношения между т очками на прямой
(предшест вует , следует за…);
От ношения между прямыми
(параллельност и, перпендикулярност и);
От ношения между геомет рическими фигурами
(равенст во, подобие, конгруэнт ност ь);
От ношения между множест вами
(объединение, пересечение, разност ь);
От ношения между высказываниями:
<=> эквивалент но (равносильно);
=> следует из другого.









 Математика
Математика








