Похожие презентации:
Понятие как форма мышления
1. Тема 2 Понятие
План лекции1)Понятие как форма мышления
и его логическая структура.
Понятие и слово.
2)Виды понятий.
3)Отношения между понятиями
по объему.
4)Логические
операции
над
понятиями и их значение для
деятельности сотрудников ОВД
2. 1А. Понятие как форма мышления
ПОНЯТИЕ–
ЭТО
ФОРМА
МЫШЛЕНИЯ,
ОТРАЖАЮЩАЯ
СУЩЕСТВЕННЫЕ
ПРИЗНАКИ
КЛАССА ПРЕДМЕТОВ.
Все
признаки
подразделяются на:
• - существенные
• -второстепенные
3.
Существенныепризнаки – это
признаки, присущие всем
предметам данного класса и
отличающие данные предметы от
всех остальных.
4. Рассмотрим пример со столом
РАССМОТРИМ ПРИМЕР СО СТОЛОМ• Нам нужно мысленно из всех
предметов, окружающих нас
выбрать столы и выделить
существенные и
второстепенные признаки.
5.
Существенные признаки:1)наличие столешницы
2)наличие какой –либо подставки, позволяющей
находиться этой столешнице выше уровня
земли или пола
6.
Второстепенные признаки:1)форма столешницы
2)материал из которого изготовлен
3) количество ножек и их вообще
наличие
7. 1в. Логическая структура понятия
Характеристики понятия:Объём понятия — это класс предметов,
обобщаемых в данном понятии.
Содержание понятия — это сумма
существенных признаков, по которым предметов
объединяются в данный класс.
8. Рассмотрим множество всех человеческих действий.
РАССМОТРИМ МНОЖЕСТВО ВСЕХ ЧЕЛОВЕЧЕСКИХДопустим, нам необходимо выделить в отдельное
ДЕЙСТВИЙ.
множество
те
действия,
которые
являются
преступлениями.
Какими
признаками
должно
обладать
действие,
чтобы
считаться
преступлением?
Оно должно быть:
1) общественно опасным
2) предусмотренным уголовным кодексом.
Все действия, обладающие данными
признаками, мы можем мысленно объединить
в один класс (в одно множество).
9.
Таким образом, мы получим понятие“преступление”, объёмом которого будут
являться все действия, попавшие в наше
множество, а содержанием — указанные
выше два признака, по которым мы
сформировали это множество.
Из этого следует
Закон обратного отношения ОБЪЕМА
СОДЕРЖАНИЯ
Чем больше содержание
понятия, тем меньше его
объем; чем меньше
содержание понятия, тем
больше его объём.
10. 1г. Понятие и слово
1Г. ПОНЯТИЕ И СЛОВОВ речи понятие выражается словом или
словосочетанием, не всегда существуют однозначные
отношения между понятием и словом. Иногда
встречаются такие слова, которые имеют множество
значений, что называется ОМОНИМИЕЙ!
Например : КОСА
11. или например: Наряд
ИЛИ НАПРИМЕР: НАРЯД• Одежда
• Распоряжение
12. 2. Виды понятий
2. ВИДЫ ПОНЯТИЙПо количеству элементов
объема понятий
подразделяются:
1.Общее понятие
2.Единичные
3.Пустые
13.
Общее― это такое понятие, объёмкоторого содержит два или более объектов.
Такими понятиями будут “самолёт”,
“дерево”, “курсант” и т. д.
Пустое― это такое понятие, понятие,
объём которого не содержит ни одного объекта.
Такими понятиями будут “Пегас”, “Император
США”, “круглый квадрат” и т. д.
Единичное ― это такое понятие, объём
которого содержит лишь один объект. Такими
понятиями будут “Москва”, “Солнце”, “Начальник
кафедры философии Санкт-Петербургского
университета МВД».
14. Классификация понятий по содержанию
1. По характеру элементов объема:а) Конкретное понятие — понятие,
элементами объёма которого являются
материальные объекты (вещи). Такими
являются понятия “стол”, “самолёт”,
“курсант”.
б) Абстрактное понятие — понятие,
элементами объёма которого являются
идеальные объекты (то есть не
существующие в материальном мире)
(свойства, отношения). Такими
понятиями являются понятия “белизна”,
“стоимость”, “вменяемость
15.
2. По наличию илиотсутствию признаков в
содержании:
a)положительные:
в
содержании
указываются
признаки
присущие
какому-либо объекту;
b)Отрицательные:
в
содержании
отрицаются
признаки
какого-либо
объекта или предмета.
16.
3. По характеру содержания:а) Безотносительное понятие —
понятия, в которых мыслятся
предметы, существующие до
известной степени самостоятельно,
независимо от других предметов.
b) Соотносительными называются
понятия, в которых мыслятся
предметы, существующие только
при наличии других предметов и
поэтому не мыслимые друг без
друга (родители― дети).
17.
4. По составу:а)
Простое
понятие
—
понятие,
содержание которого включает лишь
один
признак.
Таким
является,
например, понятие “красный цвет”, так
как его содержание составляет один
признак: “отражать световые волны
определённой частоты”.
b) Сложное
понятие
—
понятие,
содержание которого
включает более
одного
признака.
Таким
является,
например, понятие “красный предмет,
имеющий форму круга”.
18.
5. По способу объединенияэлементов в множество:
a) Собирательное понятие —понятие,
элементы
объема
которого
сами
представляют
собой
множества
объектов,
рассматриваемых
как
однородные(“толпа”,
“созвездие”,
“флот”, “флот” и т. д.).
b) Разделительное понятие — понятие,
элементы объёма которого
рассматриваются как множества
разнородных элементов. Большинство
понятий являются разделительными:
“человек”, ”студент”, ”справедливость” и
т. д.
19. 3. Отношения между понятиями
По содержанию понятия делятся насравнимые
Два понятия являются
сравнимыми,
если
и
только
если
в
их
содержаниях имеется, по
крайней мере, один общий
признак.
Такими
понятиями
являются,
например, “растение” и
”берёза”.
несравнимые.
Два понятия являются
несравнимыми, если и
только
если
в
их
содержаниях
нет
ни
одного общего признака.
Такими являются понятия
“законность”
и
”кинотеатр”.
20. 3. Отношения между понятиями
По объему сравнимые понятия делятся насовместимые
Два
понятия
совместимыми,
Несовместимые
являются Два
если
понятия
являются
и несовместимыми, если и
только если объёмы этих только если объёмы этих
понятий имеют, по крайней понятий
не
имеют
ни
мере, один общий элемент. одного общего элемента.
Такими являются понятия Такими являются понятия
“учебник”
и
”полезная
“треугольник” и ”квадрат”.
книга”.
21. Выделяют три вида совместимости:
ВЫДЕЛЯЮТ ТРИ ВИДА СОВМЕСТИМОСТИ:Виды совместимости
• Равнозначность
(тождественность)
• подчинение;
• пересечение.
22. Равнозначность
РАВНОЗНАЧНОСТЬА
В
23.
Подчинение — это отношение, при которомобъем одного понятия полностью включается в
объем другого.
Понятие В называется подчинённым (видовым)
по отношению к понятию А, а понятие А —
подчиняющим (родовым) по отношению к понятию
В. Отношение подчинения выражается в виде
следующей круговой схемы:
А
В
В отношении подчинения
находится понятие “студент”
по отношению к понятию
“учащийся”, “прокурор” по
отношению к “юрист” и т. д.
24.
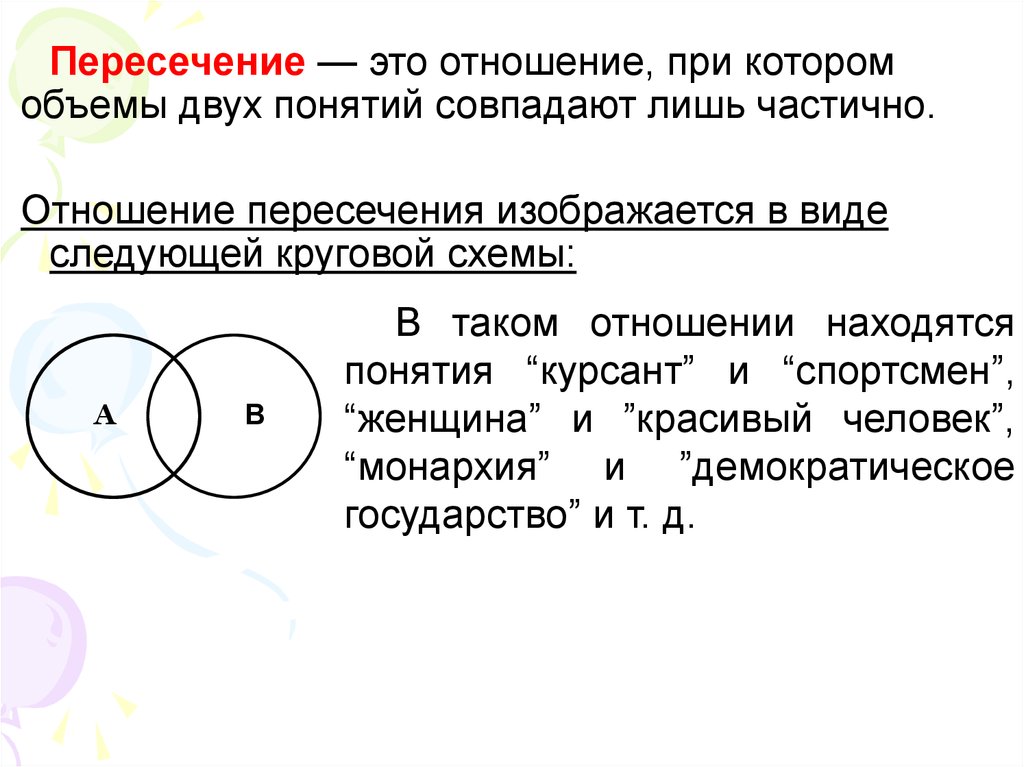
Пересечение — это отношение, при которомобъемы двух понятий совпадают лишь частично.
Отношение пересечения изображается в виде
следующей круговой схемы:
А
В
В таком отношении находятся
понятия “курсант” и “спортсмен”,
“женщина” и ”красивый человек”,
“монархия” и ”демократическое
государство” и т. д.
25.
Видовнесовместимости
существует три.
.
1.Соподчинение
2.Противоречие
3.противоположность
26. Соподчинение
СОПОДЧИНЕНИЕ— отношение, при котором 2 или более
понятий подчиняются родовому понятию и не
имеют в своих объемах общих элементов.
Например: Понятие «школьник» (А) и «студент»
(В)
соподчинены понятию
«учащийся» (С).
С
А
В
27.
Противоречие(контрадикторность) —
отношение, при котором 2 понятия
подчинены 3-му и исчерпывают весь его
объем.
Отношение противоречия выражается следующим
образом:
С
А
В (не А)
Противоречие (контрадикторность)― это отношение между двумя
понятиями, которые являются видами одного и того же рода, при этом
одно из понятий содержит определенные признаки, а другое эти же
признаки отрицает, не утверждая никаких новых признаков.
По объему два противоречащих понятия исчерпывают объем родового
понятия.
28.
В отношении противоречия находятсяпонятия “монархия” (А) и ”республика”(В, неА), так как они несовместимы и оба
подчинены понятию “форма правления
государства” (С). Кроме того, никакой другой
формы правления не существует, то есть
данные два понятия полностью исчерпывают
объём понятия “форма правления”.
29.
Противоположность(контрарность) - это
отношение, при
котором 2 понятия подчинены 3-му и
выражают крайние степени какого-либо
качества.
А С
В
Противоположность (контрарность) —
это отношение между двумя понятиями,
которые являются видами одного и того
же рода, при этом одно из понятий
содержит определенные признаки, а
другое эти же признаки отрицает,
заменяя их другими, исключающими.
По объему два противоречащих понятия
не исчерпывают объем родового
понятия.
30.
• В отношении противоположностинаходятся,
например,
понятия
“чёрный цвет” и ”белый цвет”. Они
соподчинены понятию “цвет” и
выражают две крайние степени
отражаемости
световых
волн
предметами:
предметы
чёрного
цвета поглощают все световые
волны, в то время как предметы
белого
цвета
отражают
все
световые волны. .
31. (4а) Логические операции над понятиями.
Известныследующие
операции
над
понятиями:
(1)
обобщение;
(2)
ограничение; (3) деление; (4) определение.
Обобщение
понятия
Обобщение
представляет собой переход от видового
понятия к родовому. Примером обобщения
может
служить
следующая
последовательность понятий:
школьник
→учащийся
→человек
→животное →
живой организм.
Пределом обобщения является предельно
общее понятие, называемое категорией.
32.
Ограничение понятияОграничение
представляет
собой
операцию, обратную операции обобщения
и является переходом от родового
понятия
к
видовому.
Примером
ограничения может служить следующая
последовательность понятий:
школьник ученик второго класса ученик
второго класса средней школы № 7
ученик второго класса средней школы №
7 Андрей Петров.
Пределом обобщения является единичное
понятие.
33.
Деление понятия — это логическая операция,раскрывающая объём понятия путём перечисления его
составных частей.
Структура деления представляет собой три элемента:
(1) делимое понятие;
(2) члены деления;
(3) основание деления.
Делимое понятие — это понятие объём которого
раскрывается в процессе деления.
Члены деления — это понятия, объёмы которых
являются составными частями объёма делимого
понятия.
Основание деления — признак, по которому происходит
выделение членов деления.
34.
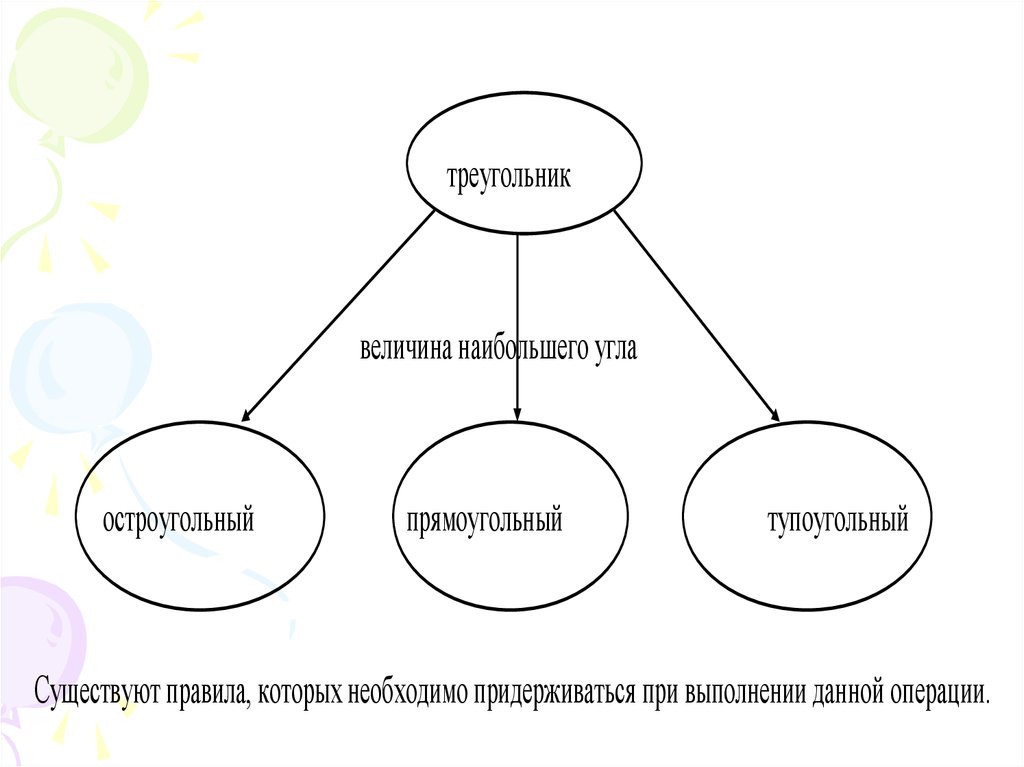
Приведём пример деления.Все
треугольники
делятся
на
остроугольные,
прямоугольные
и
тупоугольные.
В данном примере понятие “треугольник”
является делимым понятием, понятия
“остроугольный
треугольник”,
”прямоугольный
треугольник”
и
”тупоугольный
треугольник”
являются
членами деления, а признак “величина
наибольшего угла” является основанием
деления, что можно изобразить в виде
следующей схемы:
35.
треугольниквеличина наибольшего угла
остроугольный
прямоугольный
тупоугольный
Существуют правила, которых необходимо придерживаться при выполнении данной операции.
36.
1. Правило соразмерности.Сумма объёмов членов деления должна быть равна
объёму делимого понятия.
Ошибки, к которым ведёт нарушение данного правила — это
(1) неполное деление и (2) обширное деление:
Пример
неполного
деления:
Учащиеся
делятся
на
школьников и студентов.
Примером обширного деления может служить следующее:
Люди делятся на людей в возрасте от 0 до 10 лет; от 10 до
100 лет; от 100 до 500 лет; от 500 до 1000 лет.
2. Правило исключения.
Члены деления должны исключать друг друга. То есть
каждый элемент объёма делимого понятия должен входить
только в один член деления.
Пример нарушения данного правила: Письма делятся на
отправленные, неотправленные и деловые.
Видно, что член деления “деловые письма” пересекается с
двумя другими, то есть как с понятием “отправленные
письма”, так и с понятием “неотправленные письма”.
37.
3. Правило одного основания.Деление должно производиться по одному основанию.
То есть в процессе деления одного понятия в качестве
основания деления должен использоваться лишь один признак.
Пример нарушения данного правила: Треугольники делятся на
остроугольные, тупоугольные и равнобедренные.
Видно, что члены деления “остроугольные треугольники” и
”тупоугольные
треугольники”
выделяются
по
признаку
“величина
наибольшего
угла”,
а
член
деления
“равнобедренные треугольники” — по признаку “наличие двух
равных сторон”.
4. Непрерывность, последовательность.
Члены деления должны быть ближайшими видами по
отношения к делимому понятию, а признак, являющийся
основанием деления, должен изменяться постепенно,
без скачков.
Пример нарушения данного правила: Книги делятся на
учебники для школ, учебники для вузов, учебники для
техникумов, научные и художественные.
38.
Члены деления “учебники для школ”, ”учебникидля вузов” и ”учебники для техникумов” не
являются ближайшими видами, по отношению к
понятию “книги” (ближайшим видом является
понятие “учебник”).
Примером нарушения последовательности может
служить следующее деление: Дома делятся на 5этажные, 10-этажные, 1-этажные и т. д.
Видно,
что
признак
”количество
этажей”,
служащий основанием деления, изменяется не
постепенно, а скачкообразно.
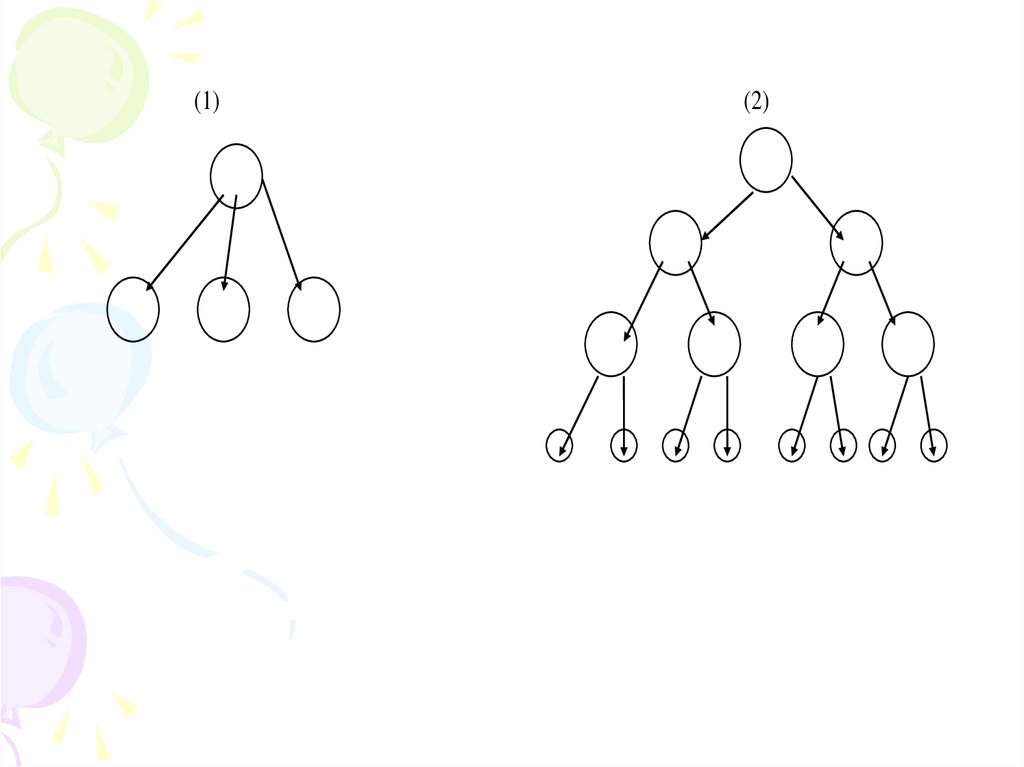
Основные виды деления. Оно может быть
(1)одноступенчатым и
(2)многоступенчатым:
39.
(1)(2)
40.
Одноступенчатое деление бывает(а) дихотомическим и
(б) делением по видоизменению признака.
Дихотомическое деление — деление, при котором
членов деления два (они находятся в отношении
противоречия).
Пример дихотомического деления: Натуральные числа
делятся на чётные и нечётные.
Деление по видоизменению признака — деление, при
котором признак, служащий основанием деления,
присущ объектам выделяемых видов в различной
степени.
Примером такого деления: Понятия делятся на пустые,
единичные и общие.
Многоступенчатое деление называется классификацией.
Классификация — систематическое распределение
элементов
какого-либо
множества
по
классам,
возникающее в результате многоступенчатого деления.
41.
Примеромклассификации
может
служить
следующее многоступенчатое деление:
Книги делятся на научные и ненаучные.
Ненаучные
делятся
на
художественные
и
учебники.
Научные
делятся
на
естественнонаучные
и
общественно-научные.
Художественные делятся на поэтические и
прозаические. Учебники делятся на учебники для
школ, учебники для техникумов и учебники для
вузов.
Существует операция, сходная с делением, но не
являющаяся
таковым.
Это
мысленное
расчленение предмета на части (так называемое
физическое или мереологическое деление).
Например:
Автомобиль
делится
на
кузов,
двигатель и шасси.
42.
Определение понятия (дефиниция) — это логическая операция,раскрывающая содержание понятия, путём перечисления
существенных признаков, входящих в него.
Пример определения:
Республика — это форма правления, при которой все граждане
имеют возможность принимать участие в формировании высших
органов государственной власти.
Определение включает себя понятие, которое определяется, и
понятие, при помощи которого определяется это первое.
Определяемое понятие и определяющее представляют собой
структуру определения.
Определяемое (дефиниендум) понятие — понятие, содержание
которого раскрывается в процессе определения.
Определяющее понятие (дефиниенс) — понятие, при помощи
которого раскрывается содержание определяемого.
При выполнении определения необходимо придерживаться
некоторых правил:
(1) соразмерности; (2) запрета круга; (3) ясности; (4)
неотрицательности.
43.
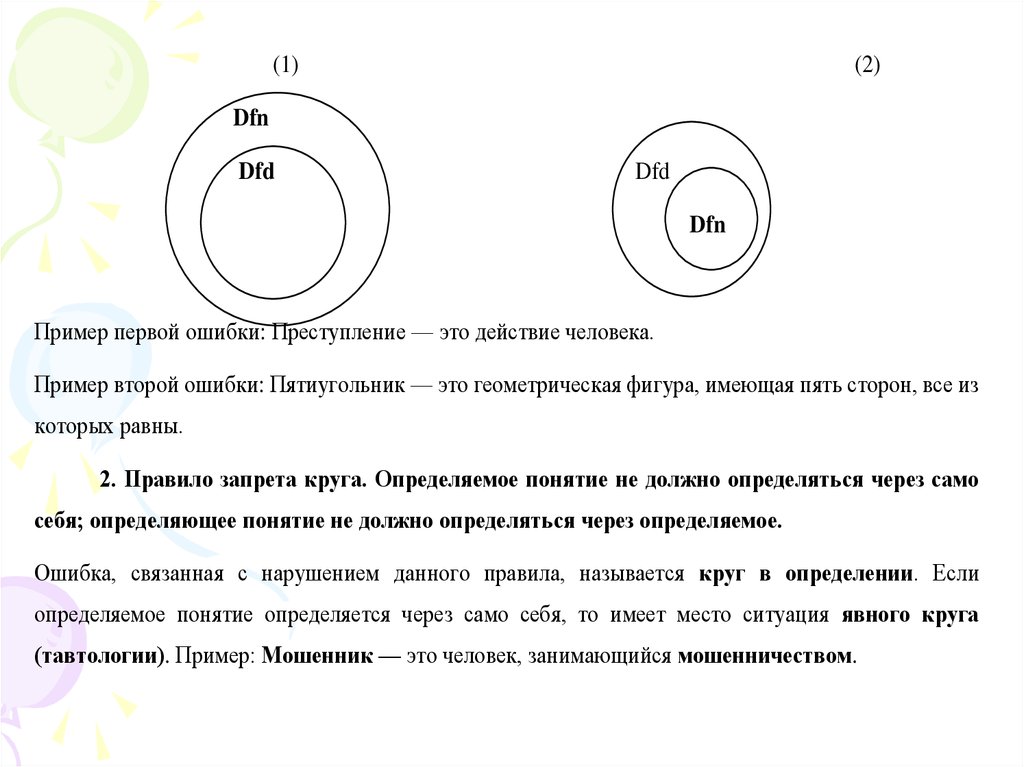
1. Правило соразмерности.Определяемое и определяющее понятия должны находиться в отношении равнозначности.
Dfd
Dfn
Наиболее распространены следующие две ошибки, связанные с нарушением данного правила:
(1) слишком широкое определение и (2) слишком узкое определение:
44.
(1)(2)
Dfn
Dfd
Dfd
Dfn
Пример первой ошибки: Преступление — это действие человека.
Пример второй ошибки: Пятиугольник — это геометрическая фигура, имеющая пять сторон, все из
которых равны.
2. Правило запрета круга. Определяемое понятие не должно определяться через само
себя; определяющее понятие не должно определяться через определяемое.
Ошибка, связанная с нарушением данного правила, называется круг в определении. Если
определяемое понятие определяется через само себя, то имеет место ситуация явного круга
(тавтологии). Пример: Мошенник — это человек, занимающийся мошенничеством.
45.
Может иметь место ситуация неявного круга, когда некотороепонятие А определяется че-рез другое понятие В, в то время
как понятие В определяется через понятие А. Например:
Законы логики — это законы, которые обеспечивают
правильные рассуждения.
Правильные рассуждения — это рассуждения, подчиняющиеся
законам логики.
3. Правило ясности. Термины, выражающие определяющее
понятие, должны быть известны и истолковываться
однозначно.
Примером нарушения этого правила может служить
следующее определение (в случае неясности термина
“перфорированный”): Решето — это сосуд с перфорированным
дном.
4. Правило неотрицательности (носит рекомендательный
характер). Определение по возможности должно быть
неотрицательным. Республика — это форма правления, не
являющаяся монархией.
46.
Основные виды определений.Существуют (1) реальные определения и
(2) номинальные.
Реальное определение — определение понятия, об
объёме и содержании которого мы уже имеем
представление (оно заранее непустое). Человек —
это животное, обладающее разумом.
Номинальное определение — определение создающее
содержание вновь вводимого понятия, об объёме
которого мы ничего не знаем (оно может быть и
пустым).
Номинальным является следующее определение:
Коллективные
образования
как
субъекты
гражданского
права
именуются
юридическими
лицами.
47.
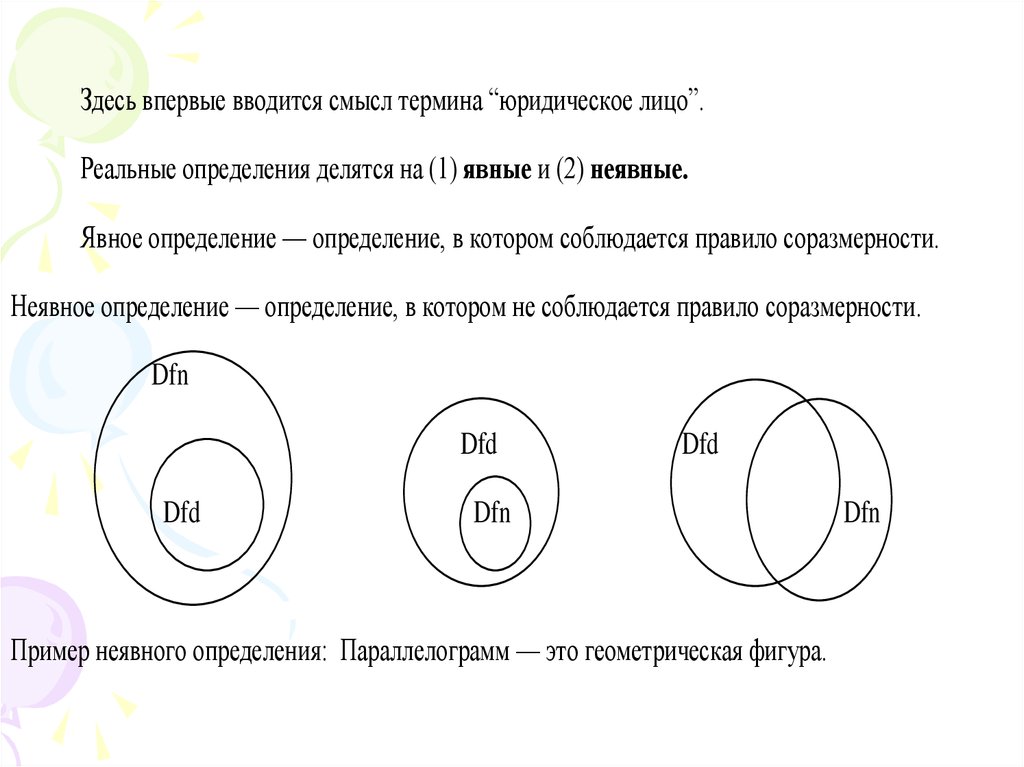
Здесь впервые вводится смысл термина “юридическое лицо”.Реальные определения делятся на (1) явные и (2) неявные.
Явное определение — определение, в котором соблюдается правило соразмерности.
Неявное определение — определение, в котором не соблюдается правило соразмерности.
Dfn
Dfd
Dfd
Dfd
Dfn
Пример неявного определения: Параллелограмм — это геометрическая фигура.
Dfn
48.
Среди явных определений наиболее распространёнными являются(1) определения через ближайший род и видовое отличие
(классическое определение) и
(2) генетическое определение.
Определение через ближайший род и видовое отличие — определение,
в котором объём определяющего понятия является пересечением
объёмов двух других понятий:
a) ближайшего родового понятия по отношения к определяемому и
b) видового отличия.
Пример:
Преступление — это общественно опасное деяние, предусмотренное
уголовным кодексом.
Понятие “преступление” определяется здесь через ближайший род
“общественно
опасное
деяние”
и
видовое
отличие
“быть
предусмотренным уголовным кодексом”.
49.
Генетическое определение — определение, в которомраскрывается способ происхождения предметов,
являющихся элементами объёма определяемого
понятия.
Пример:
Круг есть геометрическая фигура, получающаяся в
результате вращения отрезка на плоскости вокруг
одного из его концов.
(4б) Значение логических операций для деятельности
органов ОВД.
Знание правил логических операций над понятиями
позволяет выстраивать более адекватную картину
действительности,
правильно
оперировать
информацией
большого
объёма
и
избежать
непонимания при общении, что крайне необходимо в
деятельности ОВД.
50.
Литература:Основная
1. Логика: Учебник для юридических вузов / Под редакцией Сальникова В.П.,
Назаренко А.Ф., Караваева Э.Ф. Санкт-Петербургский университет МВД России. –
СПб., 2003.
2. Балахонский В.В., Назаренко А.М., Назаренко А.Ф. Логика: учебнометодическое пособие для слушателей факуль-тета заочного обучения/ Под
редакцией Сальникова В.П. Санкт-Петербургский университет МВД России. –
СПб., 2003.
3. Гетманова А.Д. Логика: Для педагогических учебных заведений. – М., 2001.
4. Ивлев Ю.В. Логика для юристов: Учебник для вузов. – М., 2000.
5. Кириллов В.И., Старченко А.А. Логика: Учебник для юридических вузов. – М.,
2002.
6. Кириллов В.И., Орлов Г.А., Фокина Н.И. Упражнения по логике/Под редакцией
В.И. Кириллова. – 4-ее изд., М., 2000.
Дополнительная
1. Брюшинкин В.Н. Практический курс логики для гуманитариев. – М., 1996.
2. Гетманова А.Д. Логика: Словарь и задачник: Учебное пособие для студентов
вузов. – М., 1997.
3. Демидов И.В. Логика: Учебное пособие для юридических вузов/Под редакцией
Б.И. Каверина. – М., 2000.
6. Ивин А.А. Логика: Учебник. – М., 2001.
7. Кириллов В.И. Логика: Учебное пособие. – М., 2003.
8. Михалкин Н.В. Логика и аргументация в судебной практике. – СПб., 2004.













































 Философия
Философия








