Похожие презентации:
Планы второго порядка. Композиционные планы Бокса-Уилсона
1. ПЛАНЫ ВТОРОГО ПОРЯДКА
Композиционные планы БоксаУилсона2.
Линейная математическая модель, описывающая зависимость отклика «у» отфакторов xj довольно часто оказывается неадекватной эксперименту.
В этом случае линейность зависимости теряется. Тогда следует переходить к
полиномиальной модели второго порядка.
2
3.
Число коэффициентов l в полиноме второго порядкаl = k+ 1 +k + C2k
(2)
k - коэффициенты при xj в первой степени,
k - коэффициенты при квадратичных членах,
C2k - количество сочетаний из k факторов по 2, равное числу эффектов
парного взаимодействия
,
(k+ 1)(k+2)
l=
2
3
4.
Если факторов всего два, т.е. две переменных на трех уровнях, то число опытов N = 32 = 9 .Число членов в модели l = (2+1)(2+2) / 2 = 6
Вид модели:
геометрическим образом является квадрат, экспериментальные точки располагаются
в его вершинах, по центрам граней и в центре.
4
5.
Форма матрицы планирования ПФЭ 325
6.
Форма матрицы планирования ПФЭ 32 приведена в таблице№опыта
х1
х2
у
№опыта
х1
х2
у
1
─
─
у1
6
─
0
у6
2
+
─
у2
7
0
+
у7
3
─
+
у3
8
0
─
у8
4
+
+
у4
9
0
0
у9
5
+
0
у5
6
7.
Матрица ПФЭ 33 состоит из 27 опытовгеометрический образ – куб;
планируемые точки расположены в его вершинах, в
центрах ребер, в центрах граней и одна – в центре куба.
Всего 27 точек.
7
8.
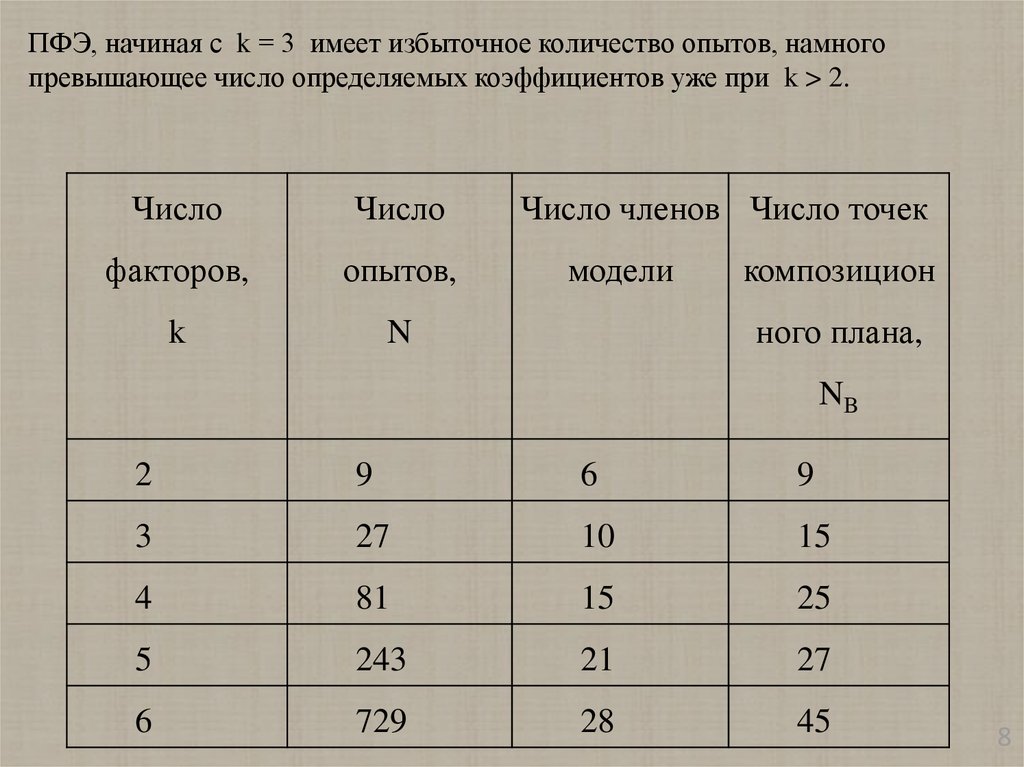
ПФЭ, начиная с k = 3 имеет избыточное количество опытов, намногопревышающее число определяемых коэффициентов уже при k > 2.
Число
Число
факторов,
опытов,
k
N
Число членов Число точек
модели
композицион
ного плана,
NB
2
9
6
9
3
27
10
15
4
81
15
25
5
243
21
27
6
729
28
45
8
9.
Сократить число опытов можно, если воспользоваться такназываемым композиционным или последовательным планом,
предложенным Боксом и Уилсоном.
Ядро такого плана составляет ПФЭ 2k при k < 5 или
полуреплика от него при k > 5
Возможность
использования
в качестве ядра плана
полуреплики при k > 5 обусловлена тем, что уже полуреплика
обеспечивает получение несмешанных оценок для линейных
эффектов и эффектов парных взаимодействий.
9
10.
ПФЭ 2k или его полуреплика дополняются определеннымчислом так называемых «звездных точек», расположенных
на координатных осях факторного пространства и точками в
центре плана.
NB = NI + Nα +N0,
NI- число точек ПФЭ 2k;
Nα- число «звездных» точек, равное 2k;
N0- число точек в центре плана.
10
11.
Число опытов в матрице композиционного плана второгопорядка при k факторах составляет
NB = 2k + 2k + N0 при k < 5
NB = 2k-1 + 2k + N0 при k > 5
11
12.
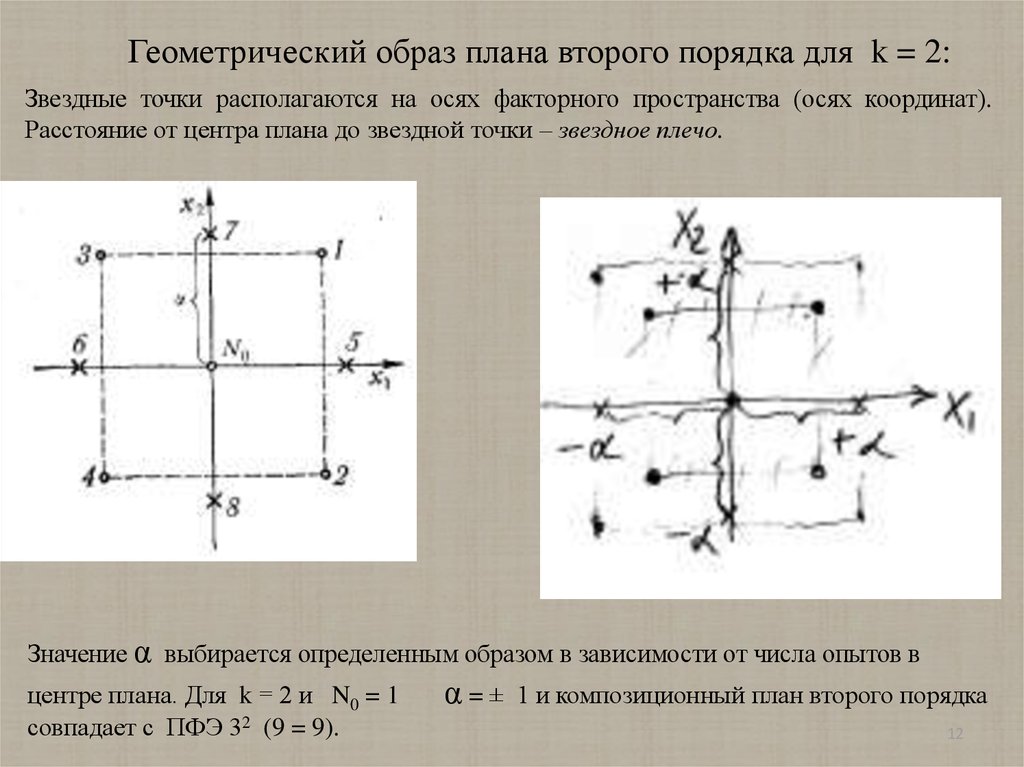
Геометрический образ плана второго порядка для k = 2:Звездные точки располагаются на осях факторного пространства (осях координат).
Расстояние от центра плана до звездной точки – звездное плечо.
Значение α выбирается определенным образом в зависимости от числа опытов в
центре плана. Для k = 2 и N0 = 1
совпадает с ПФЭ 32 (9 = 9).
α=±
1 и композиционный план второго порядка
12
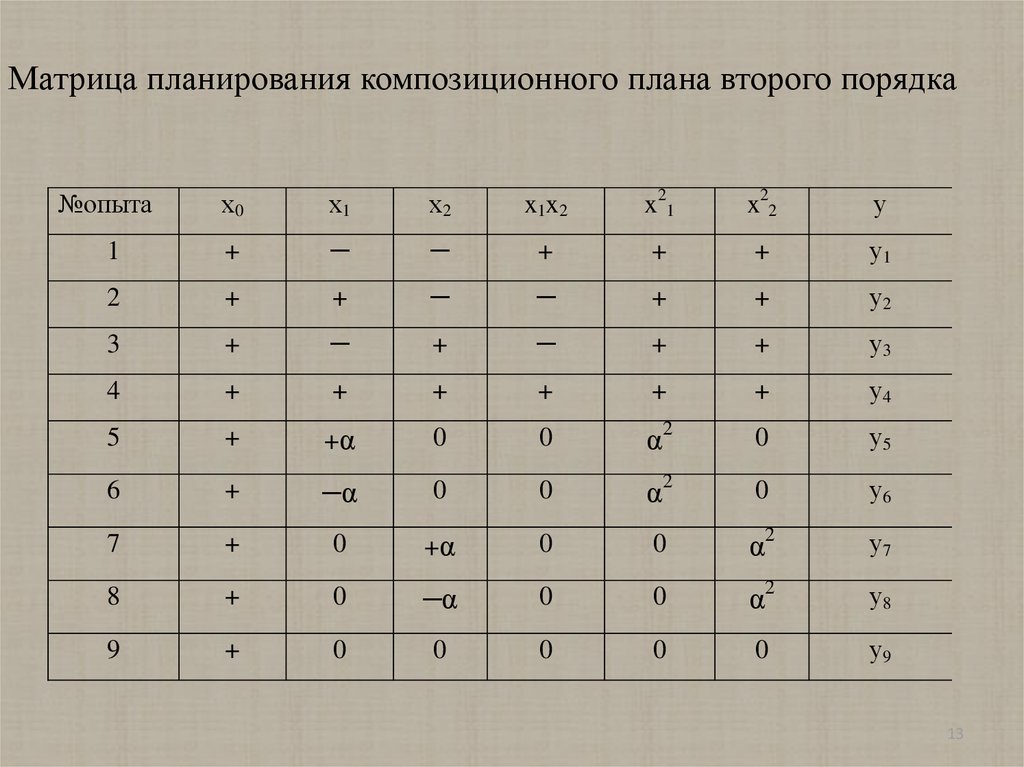
13.
Матрица планирования композиционного плана второго порядках0
х1
х2
x1x2
x21
x22
у
1
+
─
─
+
+
+
у1
2
+
+
─
─
+
+
у2
3
+
─
+
─
+
+
у3
4
+
+
+
+
+
+
у4
5
+
+α
0
0
α2
0
у5
6
+
─α
0
0
α2
0
у6
7
+
0
+α
0
0
α2
у7
8
+
0
─α
0
0
α2
у8
9
+
0
0
0
0
0
у9
№опыта
13
14.
Если k = 3, Nb = 23 +2·3 + 1 = 15k = 4, Nb = 24 +2·4 + 1 = 25
k
=5
Nb = 25 +2·5 + 1 = 43
начиная с
k > 5 в основу плана кладется дробный
факторный эксперимент – полуреплика от ПФЭ 2k.
k = 5 Nb = 25-1 +2·5 + 1 = 27
Для k = 3 Nb = 15 вместо 27 ( см слайд 8)
нет точек на серединах ребер, только вершины куба, центры граней и центр самого куба.
14
15.
композиционные планы второго порядка неортогональны:15
16.
Композиционные планы приводятся к ортогональному видувыбором соответствующего звездного плеча α.
в зависимости от числа опытов в центре плана N0 и числа
факторов k можно выбрать величину звездного плеча α таким
образом, чтобы матрица планирования стала ортогональной.
В зависимости от N0 и k α. должны иметь следующие
значения:
k
Ядро плана
N0=1
Значения α
2
3
4
5
22
23
24
25-1
1,215
1,414
1,547
1,000
для различного числа факторов и одного опыта в центре плана
16
17.
Значения α2 для различного числа факторов и количестваопытов в центре плана
N0
k
2
3
4
5*
1
1,000
1,476
2,000
2,390
2
1,160
1,650
2,164
2,580
3
1,317
1,831
2,390
2,77
4
1,475
2,000
2,580
2,950
5
1,606
2,164
2,770
3,140
* - для k = 5 в ДФЭ25-1 используется полуреплика
х5 = х1х2х3х4
17
18.
Выбрав α из таблицы и проведя следующее линейноепреобразование квадратичных столбцов xj2
получим ортогональную матрицу
18
19.
Построим ортогональный план второго порядка для k= 2 и n0 = 1.В отличие от ранее приведенной матрицы планирования ПФЭ 32,
вектор-столбцы, соответствующие x12 и x22 , заменяются новыми
переменными x1' x2' , которые определяются по формуле
Для ортогонального плана второго порядка, если
Те же значения будет принимать и x2'
N0 = 1
19
20.
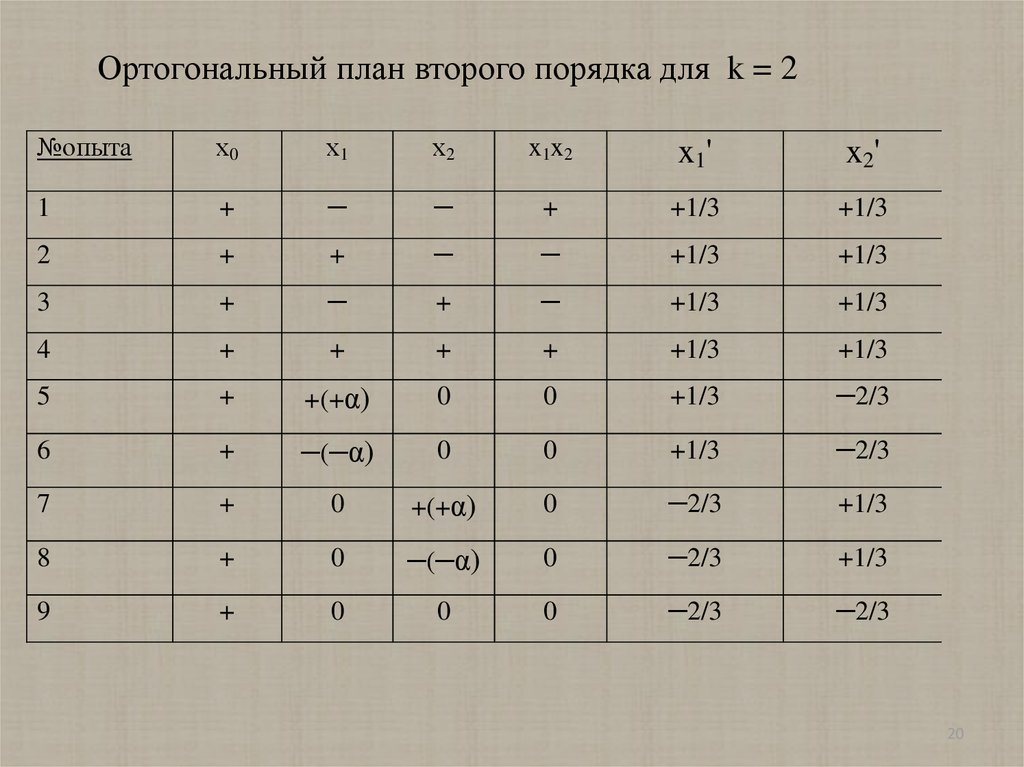
Ортогональный план второго порядка для k = 2№опыта
х0
х1
х2
x1x2
x1'
x2'
1
+
─
─
+
+1/3
+1/3
2
+
+
─
─
+1/3
+1/3
3
+
─
+
─
+1/3
+1/3
4
+
+
+
+
+1/3
+1/3
5
+
+(+α)
0
0
+1/3
─2/3
6
+
─(─α)
0
0
+1/3
─2/3
7
+
0
+(+α)
0
─2/3
+1/3
8
+
0
─(─α)
0
─2/3
+1/3
9
+
0
0
0
─2/3
─2/3
20
21.
Другой вариант построения21
22.
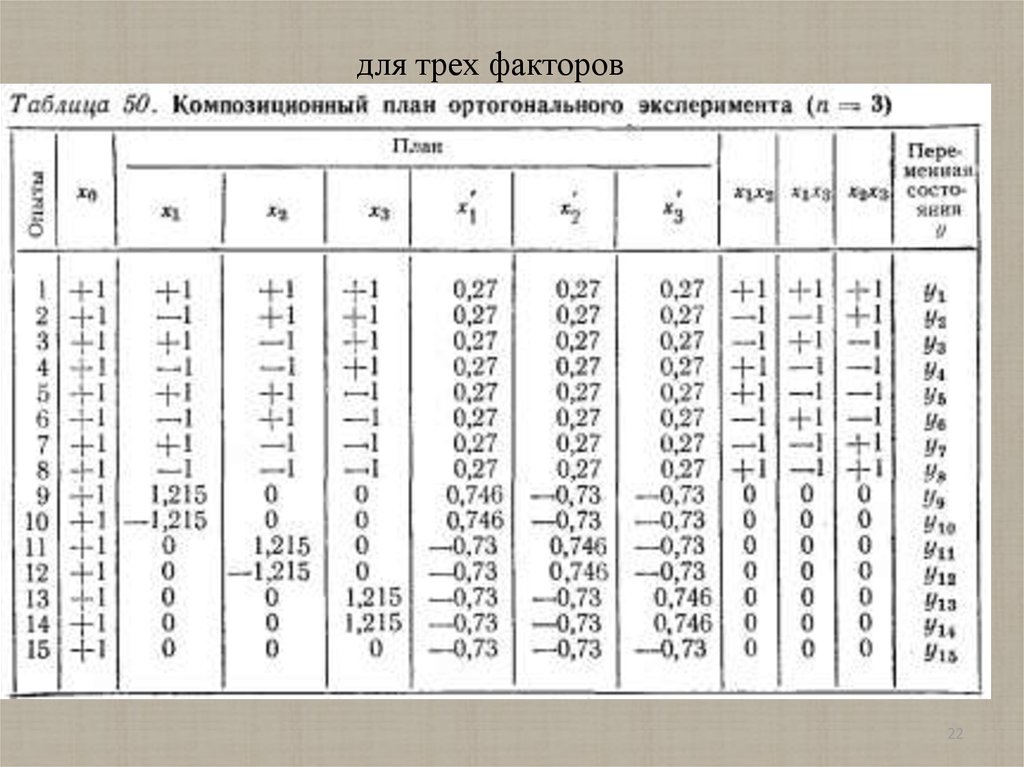
для трех факторов22
23.
Благодаря ортогональности матрицы планирования, всекоэффициенты модели определяются независимо друг от друга
по формуле
Дисперсии коэффициентов равны s2bj
23
24.
В результате расчетов по матрице с преобразованнымистолбцами для квадратичных эффектов получим уравнение
24
25.
Чтобы перейти к обычной записи, определяют b0 по формулеПосле замены b0' на b0 (без штриха) уравнение имеет обычный
вид
25
26.
Хотя формулы для определения дисперсий коэффициентов вобщем виде выглядят одинаково
однако для разных столбцов матрицы планирования
будет иметь разные численные значения.
Следовательно, коэффициенты регрессии для ортогональных
планов второго порядка будут определяться с разной точностью.
26
27.
Ортогональные планы второго порядка не обладают свойствомрототабельности, т.к. на равных расстояниях от центра плана
дисперсия для «у» будет различной.
27
28.
2829.
2930.
3031.
3132.
Принятие решений по планам второго порядкаНелинейная модель адекватна. Если целью было получение
интерполяционной модели (описывающей область оптимума), то
исследование заканчивается.
Нелинейная модель неадекватна.
Переход к моделям
третьего порядка считается неэффективным из-за сложностей в
планировании и вычислительных операциях.
Необходимо: ввести новые факторы; увеличить число опытов;
учесть возможность временного дрейфа.
32




























 Математика
Математика








