Похожие презентации:
Электромагнетизм
1. ФИЗИКА
Лекция № 12.
Литература1.Хавруняк В. Г. Курс физики. - М.: НИЦ ИНФРА-М, 2014.
- 400 с. - ЭБС "Знаниум".
2. Рогачев Н. М. Курс физики. - М.: Лань, 2010. - 448 с. –
ЭБС "Лань".
3. Трофимова Т.И. Курс физики.- М. : Академия, 2010. 560 с.
4. «Физика. Лабораторный практикум» . - ЭБС «ВГЛТУ»
1. «Магнетизм»
2. «Колебания и волны»
3. «Волновая оптика»
2
3. ЭЛЕКТРОМАГНЕТИЗМ
34.
Под электромагнитным полем (ЭМП)понимают вид материи, характеризующийся
совокупностью взаимосвязанных и
взаимообусловливающих друг друга
электрического и магнитного полей.
Электромагнитные поля оказывают на
заряженные частицы силовое воздействие и
определяются во всех точках двумя парами
векторных величин, которые характеризуют две
его стороны - электрическое и магнитное поля.
Взаимодействие заряженных частиц друг с
другом осуществляется посредством
электромагнитного поля.
4
5.
Электрическое поле –это составляющая ЭМП, которая
характеризуется воздействием на электрически
заряженную частицу с силой,
пропорциональной заряду частицы и не
зависящей от ее скорости.
Источником электрического поля
являются электрические заряды или
переменное магнитное поле.
Неподвижные электрические заряды
являются источником электростатического поля
(электростатика).
5
6.
Магнитное поле –это составляющая ЭМП, которая характеризуется
воздействием на движущуюся частицу с силой,
пропорциональной заряду частицы и ее скорости.
Магнитное поле действует на тела, обладающие
магнитным моментом.
Источником магнитного поля являются
движущиеся электрические заряды (токи),
намагниченные тела или переменное
электрическое поле.
При равномерном и прямолинейном
движении заряда (или постоянном токе)
возникает постоянное магнитное поле
(магнитостатика).
6
7.
Ханс Кристиан Э́рстед1777 - 1851
Датский ученый, физик,
исследователь
явлений электромагнетизма.
7
8.
,где
Магнитная индукция –
это силовая характеристика магнитного поля.
За направление вектора магнитной индукции B
принимается направление северного конца
свободной магнитной стрелки, установившейся в
данной точке поля.
8
9.
Магнитное поле оказывает ориентирующеедействие и на контур с током. Поэтому контур (рамка,
виток) с током является удобным инструментом для
исследования и измерения магнитного поля.
Размеры контура должны быть настолько малы,
чтобы в его пределах исследуемое магнитное поле можно
считать однородным.
За направление вектора B принимается
направление положительной нормали n
к плоскости свободного контура с током,
установившегося в магнитном поле.
Нормаль считается положительной, если
ее направление совпадает с
направлением поступательного движения
правого винта при его вращении по
направлению тока в контуре.
9
10.
[B]. =
.
Модуль вектора магнитной индукции
равен отношению максимального момента сил,
действующего на пробный контур, к магнитному
моменту этого контура:
M max M max
B
pM
IS
где
I - сила тока в контуре;
S – площадь, ограниченная контуром;
p ISn - магнитный момент контура.
M
Единицей измерения магнитной индукции в СИ является
тесла (Тл):
Н м
2
А м
Дж
А м
2
В А с
2
А м
В с
2
м
Тл
10
11. Закон Био-Савара-Лапласа
,,
Элемент dl проводника с постоянным
током I создает в точке M,
расположенной на расстоянии r от него
магнитное поле, индукция которого
определяется выражением:
0 I
dB
[dl r ]
3
4 r
0 I
dB
dl sin
2
4 r
r - радиус-вектор, проведенный от начала элемента dl в
рассматриваемую точку M;
µ - магнитная проницаемость среды (для вакуума µ = 1);
o 4 10 7
Гн/м – магнитная постоянная.
12.
,Индукция магнитного поля, созданного всем
проводником с током, согласно принципу
суперпозиции определяется интегрированием по всей
длине L проводника:
B dB
L
Индукция магнитного поля прямолинейного бесконечного
проводника с током на расстоянии rо от него
2 o
B
I
4 ro
Индукция магнитного поля в центре кругового проводника
радиуса R с током
B
Индукции магнитного поля заряда q, движущегося со
скоростью v
q
B
o
4 r
3
o I
2R
[v r ]
12
13.
Сила Лоренца это сила, действующая на движущийся в электромагнитномполе заряд:
F qE q[v B ]
Первый компонент не зависит от скорости движения заряда и называется
электрической составляющей силы Лоренца:
Fэ qE
Второй компонент называется магнитной составляющей силы Лоренца,
который возникает только при движении заряда:
Fм q[v B ]
Направление вектора Fм для положительных
зарядов определяется правилом левой руки.
13
14.
Вектор Fм перпендикулярен плоскости, вкоторой расположены векторы B и v , т.е.
Fм B
и
Fм v
Поэтому магнитная составляющая силы
Лоренца не совершает работу, то есть с
помощью магнитного поля нельзя изменить
энергию заряженной частицы.
Составляющая Fм сообщает заряду
нормальное ускорение, то есть изменяет лишь
направление скорости, а не ее модуль.
15.
Модуль магнитной составляющей силы Лоренцазависит от направления движения заряда в магнитном
поле:
Fм qvB sin
Радиуса R кривизны траектории при движении
заряда по окружности:
mv
R
qB
15
16.
Сила АмпераЕсли проводник с током находится в магнитном поле, то на движущиеся
в проводнике носители тока со стороны магнитного поля действует магнитная
составляющая силы Лоренца. Векторная сумма этих сил это и есть сила,
действующая на проводник с током в магнитном поле – сила Ампера.
Сила, действующая на элемент проводника с
током в магнитном поле:
dF I [dl B ]
Интегрируя это выражение по длине проводника, можно получить
силу Ампера, действующую на весь проводник. В частности, если
проводник целиком находится в однородном магнитном поле, то на него
действует сила
F IlBsin
где α - угол между направлением тока и вектором
B
.
16
17.
Направление силы Ампера F определяетсяА
так же по правилу левой руки, как и
направление
магнитной составляющей силы
Лоренца FМ , действующий на движущиеся в
электромагнитном поле положительные
заряженные частицы.
Сила Ампера – основа работы электродвигателей
и приборов магнитоэлектрической системы.
17
18.
Циркуляция вектора магнитнойиндукции в вакууме
,
Для электростатического поля циркуляция вектора
напряженности E вдоль замкнутого контура равна работе по
перемещению положительного единичного заряда по замкнутой
траектории L. Так как электростатическое поле потенциально, то
работа, а, следовательно, и циркуляция вектора равна нулю:
(E , dl ) 0
L
Циркуляция вектора магнитной индукции
вдоль замкнутого контура L определяется по
аналогичной формуле:
B
(B , dl ) B dl cos
L
L
18
19.
.Вычислим этот интеграл для магнитного поля
прямолинейного бесконечного проводника с током I. В качестве
замкнутого контура L выберем произвольную линию магнитной
индукции, которая имеет форму окружности с центром на
проводнике. В таком случае угол = 0, а модуль вектора в любой
точке этой окружности одинаков и равен:
I
B
o
2 R
где R – радиус окружности. Тогда
I
(B , dl )
dl I
2 R
o
L
L
o
Этот результат носит универсальный
характер и справедлив для магнитного поля,
созданного проводником любой формы и любого
замкнутого контура. Проводники с током,
находящиеся вне контура, не вносят вклад в
циркуляцию вектора магнитной индукции.
19
20.
Если магнитное поле создано несколькими (n )проводниками с токами, то в соответствии с принципом
суперпозиции:
n
(B , dl ) I
L
o
i 1
охв
i
Закон полного тока для магнитного поля в вакууме:
циркуляция вектора магнитной индукции вдоль любого
замкнутого контура в вакууме равна произведению
магнитной постоянной на алгебраическую сумму токов,
которые охватывает этот контур.
Существенно, что циркуляция не равна нулю, то есть магнитное
поле не потенциально. Такое поле называется вихревым.
Закон полного тока удобен при расчете магнитных полей. При этом
он применяется совместно с законом Био-Савара-Лапласа.
20
21.
,где
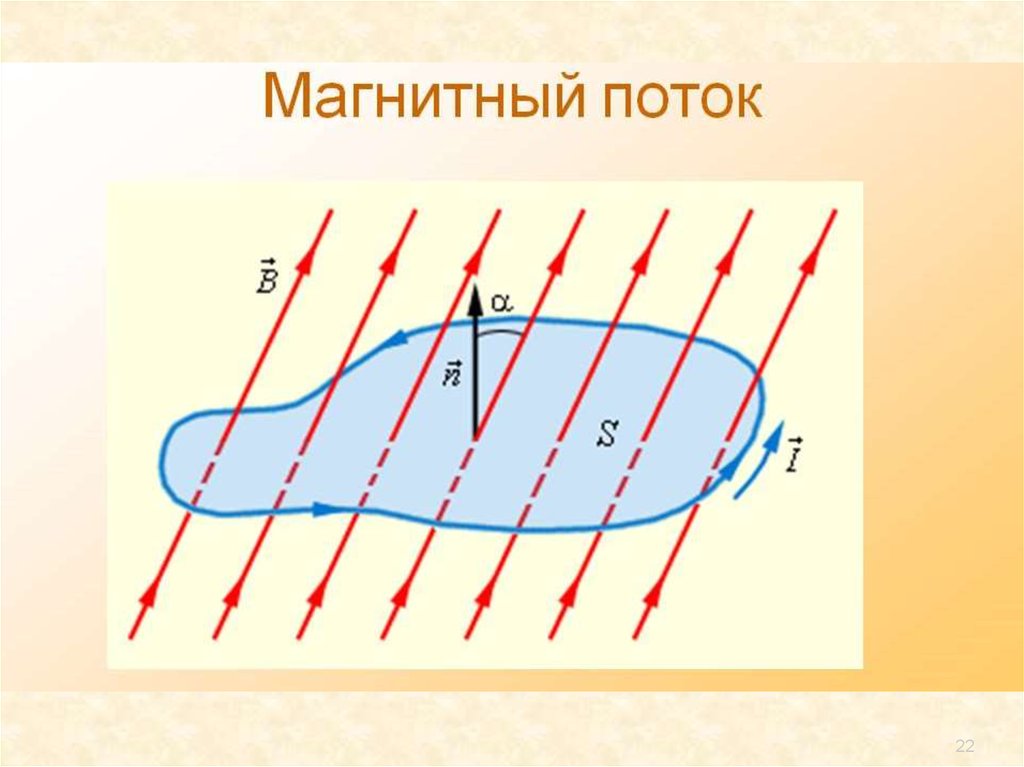
Магнитный поток (поток вектора магнитной
индукции) через элементарную площадку dS
d (B , dS ) B dS cos
м
- угол между вектором
B и перпендикуляром к плоскости dS..
Для поверхности конечной площади S
(B , dS ) B dS
м
S
S
n
Единицей измерения магнитного потока в
СИ является вебер (Вб): [Ф] = Тл·м2 = Вб.
Магнитный поток через
поверхность любую поверхность S
пропорционален числу линий магнитной
индукции, пронизывающих данную
поверхность.
21
22.
2223.
..
Теорема Гаусса для магнитного поля в вакууме:
магнитный поток через любую замкнутую
поверхность равен нулю
Bn dS 0
S
Это следует из того, что линии индукции магнитного
поля замкнуты (в природе нет магнитных зарядов),
поэтому число таких линий, входящих в любую
замкнутую поверхность равно числу линий, выходящих
из этой поверхности.
24.
Работа по перемещению проводникаи контура с током в магнитном поле
Пусть прямолинейный проводник длиной l с постоянным
током I находится в однородном магнитном поле, при этом вектор B
перпендикулярен проводнику. На проводник действует сила Ампера
F IBl
При малом перемещении dr проводника эта сила совершает
элементарную работу
A F dr IBl dr IB dS I d м
При конечном перемещении проводника из
положения 1 в положение 2 работа равна
2
2
1
1
A A I d I
м
12
м
Эта формула справедлива для проводника любой
формы и при любой ориентации вектора B .
25.
Работа силы Ампера при перемещении проводника спостоянным током в магнитном поле, равна произведению силы
тока в проводнике на магнитный поток через поверхность,
прочерченную проводником при его движении:
A I
12
М
Работа перемещения замкнутого контура с постоянным
током в магнитном поле равна произведению силы тока в
контуре на изменение магнитного потока через поверхность,
ограниченную этим контуром:
A I
12
М
Данная работа совершается не за счет энергии
магнитного поля, а за счет энергии источника тока,
создающего ток в контуре.
25
26. Электромагнитная индукция
2627.
Явление электромагнитной индукции:возникновение индукционного тока в замкнутом
проводящем контуре при изменении магнитного
потока через поверхность, ограниченную этим
контуром.
Появление индукционного тока
говорит о возникновении в контуре
электродвижущей силы.
Фарадей
установил,
что
величина ЭДС не зависит от способа
изменения магнитного потока и
определяется лишь скоростью его
изменения.
Майкл Фарадей
1791-1867
27
28.
Способы изменения магнитного потока,
B S cos
м
1. Контур деформируется в магнитном поле (изменяется
величина S);
2. Контур поворачивается в магнитном поле (изменяется угол );
3. Контур движется в неоднородном стационарном магнитном
поле (изменяется величина В);
4. Неподвижный контур находится в нестационарном магнитном
поле (магнитное поле переменно).
28
29.
.В способах 1, 2 и 3 проводник движется в
стационарном магнитном поле. Вместе с проводником в
магнитном поле движутся и его свободные заряды, на
каждый из которых действует магнитная составляющая
силы Лоренца, которая приводит к разделению зарядов. То
есть магнитная составляющая силы Лоренца играет
роль сторонней силы, которая и приводит к появлению ЭДС
индукции.
В способе 4 проводник неподвижен, поэтому
магнитная составляющая силы Лоренца на его свободные
заряды не действует. Согласно Максвеллу, изменяющееся
во времени магнитное поле приводит к появлению в
пространстве вихревого электрического поля. В этом
случае на свободные заряды проводника действует
электрическая составляющая силы Лоренца, которая и
приводит к разделению зарядов, то есть к появлению ЭДС
индукции.
29
30.
Закон электромагнитной индукцииЭДС электромагнитной индукции, возникающая в
проводящем контуре, равна и противоположна по
знаку скорости изменения магнитного потока
через поверхность, ограниченную этим контуром:
d
E
dt
м
i
В способе 4 неподвижный контур находится в переменном
магнитном поле B(t). В этом случае сторонней силой является
электрическая составляющая силы Лоренца
Fстор Fэ qE
где E - напряженность непотенциального (вихревого)
электрического поля, которое возникает при изменении
магнитного поля.
30
31.
, Используягде
определение ЭДС и закон электромагнитной
индукции, можно получить:
Bn
E dl t dS
L
S
циркуляция вектора напряженности электрического поля вдоль
произвольного замкнутого контура L равна и противоположна
по знаку скорости изменения магнитного потока через
поверхность S, ограниченную этим контуром.
То есть, изменяющееся во времени
магнитное поле порождает вихревое
электрическое поле.
Это одно из уравнений Максвелла.
31
32. Правило Ленца:
Индукционный ток при электромагнитной индукциивсегда направлен так, что созданное им магнитное
поле противодействует изменению магнитного потока,
который вызвал этот ток.
Так система проявляет
свойство инерции.
Правило Ленца является
следствием закона
сохранения энергии.
32
33.
..
Явление самоиндукции
Пусть замкнутый проводящий контур подключен к источнику
тока Е. Тогда в контуре течет электрический ток I, который создает
вокруг проводника магнитное поле. Можно определить магнитный
поток Фм этого поля через поверхность S, ограниченную данным
контуром:
м L I
где величина L называется
индуктивностью контура.
Если источник тока вызывает в
контуре постоянный ток, то вокруг
проводника возникает постоянное
магнитное поле, и следовательно,
магнитный поток Фм будет
постоянным во времени. Ничего
интересного не происходит.
34.
Если источник тока вызывает в контуре переменный ток,то вокруг проводника возникает переменное магнитное поле, и
магнитный поток Фм через поверхность, ограниченную контуром,
будет переменным во времени. Следовательно , в контуре возникнет
кроме Е еще одна ЭДС, которую называют ЭДС самоиндукции:
d(L I )
Е
dt
s
dL
dI
L
I
dt
dt
Если индуктивность L контура постоянна, то ЭДС самоиндукции
dI
Е L
dt
s
ЭДС самоиндукции пропорциональна скорости изменения силы
тока в контуре. Знак минус показывает, что ЭДС самоиндукции всегда
препятствует изменению силы тока в контуре.
Индуктивность является мерой инертности контура и в этом
смысле она аналогична массе в механике. Система стремится
сохранить магнитный поток через контур постоянным.
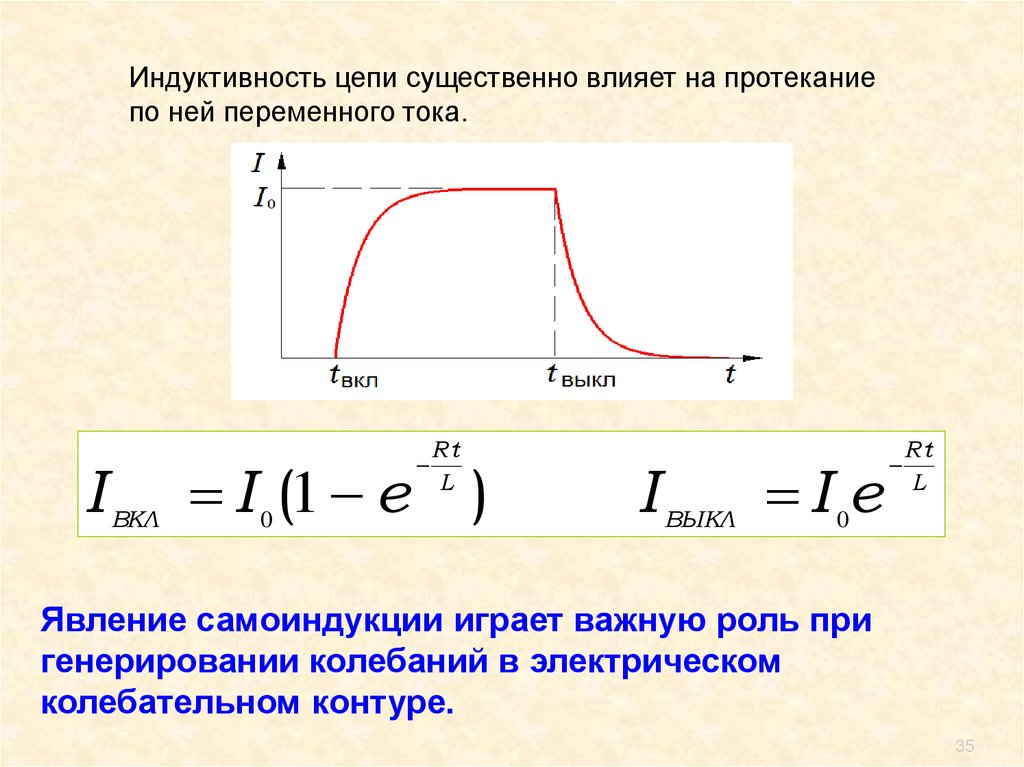
35.
Индуктивность цепи существенно влияет на протеканиепо ней переменного тока.
I
ВКЛ
I (1 e
0
Rt
L
)
I
ВЫКЛ
I e
Rt
L
0
Явление самоиндукции играет важную роль при
генерировании колебаний в электрическом
колебательном контуре.
35
36. Энергия магнитного поля
Если ключ К находится в положении 1, тов катушке течет постоянный ток I, который
создает стационарное магнитное поле.
Если ключ К переключить в положение 2,
то сила тока в катушке будет уменьшаться, и в
ней возникнет ЭДС самоиндукции. Работа,
совершаемая этим током за время dt, равна
dI
A Е is I dt L I dt L I dI
dt
Интегрируя это выражение от первоначального значения силы тока I
до нуля, получим работу в цепи за все время изменения тока
LI2
A L I dI
2
I
0
37.
Отсюда следует, что магнитное поле является носителемэнергии, за счет которой и совершается эта работа. Таким
образом, энергия магнитного поля в катушке
LI
Wм
2
2
Энергию магнитного поля можно выразить через величины,
характеризующее само поле, если использовать
L n V
2
0
B 2V
2 o
B In
Wм
0
N
n
l
V Sl
В рассматриваемом случае магнитное поле и его энергия локализованы
внутри катушки. Отсюда плотность энергии магнитного поля
2
wм
Wм
B
V
2 o
37
38. Электромагнитное поле в веществе
При внесении вещества в электромагнитноеполе наблюдается воздействие на заряды и
магнитные моменты молекул вещества.
Электромагнитное поле оказывает
ориентирующее действие на дипольные и
магнитные моменты молекул вещества.
38
39.
.Электрическое поле в
веществе
Все вещества по их электрическим свойствам
можно разделить на проводники, полупроводники и
диэлектрики.
Диэлектрики бывают:
неполярные,
полярные,
сегнетоэлектрики.
Система двух разноименных
одинаковых по модулю
электрических зарядов называется
электрическим диполем.
Дипольным моментом называется
вектор
pe ql
39
40.
,При внесении диэлектриков в электрическое
поле происходит явление поляризации. Механизм
этого явления зависит от строения молекул
диэлектрика.
Молекулы неполярного диэлектрика
симметричны, «центры тяжести» положительных и
отрицательных зарядов совпадают (l = 0).
Собственный дипольный момент молекул
неполярных диэлектриков равен нулю.
Во внешнем электрическом поле происходит
смещение зарядов (деформация молекулы). В
результате молекула приобретает дипольный момент,
направленный по полю.
40
41.
.Молекулы полярного диэлектрика имеют
отличные от нуля собственные дипольные моменты,
но до внесения в поле эти моменты ориентированы
хаотично, что поддерживается тепловым движением.
При внесении полярного диэлектрика в
электрическое поле возникает преимущественная
ориентация диполей по направлению поля, но
тепловое движение мешает этому процессу.
Количественной мерой поляризации любого
диэлектрика является вектор поляризованности
P lim
V 0
pei
V
V
– это электрический (дипольный) момент единицы объема.
41
42.
Значение напряженности электрического поля Еиспытывает скачок на границе раздела сред.
Для расчета влияния диэлектрика вводят такую
характеристику, которая зависит только от
источников внешнего поля и оказывается одинаковой
для любой среды.
Такой характеристикой является вектор
электрического смещения (электрическая
индукция):
D oE P
42
43.
.Электрическое смещение (электрическая индукция):
D oE P
При переходе из одной среды в другую величина D не
изменяется, в то время как значение напряженности
электрического поля Е испытывает скачок на границе раздела
сред с различными свойствами.
44.
Поляризованность пропорциональнанапряженности
внешнего поля:
,
P o E
где
Величина называется электрической
восприимчивостью, она показывает, насколько
вещество воспринимает поле.
D o ( 1 )E o E
Величина
1
называется диэлектрической проницаемостью.
Электрическое смещение (электрическая
индукция) D - это характеристика источника
электрического поля, которым являются
свободные заряды.
44
45.
..
Вспомним, что для вакуума
E ( E dS )
S
1
n
внутри
qi
o i 1
где суммируются все свободные заряды в объеме,
ограниченном замкнутой поверхностью S. Других зарядов в
вакууме просто нет.
Вектор D от свойств среды не зависит, он описывает
электростатическое поле, созданное свободными
зарядами, но при таком их расположении, которое
устанавливается при наличии диэлектрика.
46. Теорема Гаусса для электростатического поля в диэлектрике:
( D dS )S
n
своб .
qi
i 1
Поток вектора смещения электростатического
поля в диэлектрике через произвольную замкнутую
поверхность равен алгебраической сумме
свободных зарядов внутри этой поверхности.
46
47. Магнитное поле в веществе
4748.
Магнитным моментом контура с током I называется векторpм I Sn
где S – площадь, ограниченная контуром;
n – положительная нормаль к плоскости контура.
При рассмотрении молекул под I понимают орбитальный ток,
а под S – площадь «орбиты» электрона.
49.
.Все вещества реагируют на действие магнитного
поля, т.е. являются магнетиками.
По магнитным свойствам вещества можно
разделить на диамагнетики, парамагнетики и
ферромагнетики.
Количественной мерой степени
намагничивания вещества является
вектор намагниченности
J lim
V 0
p мi
V
V
– это магнитный момент единицы объема вещества.
49
50.
В диамагнетиках собственныемагнитные моменты молекул равны нулю.
При внесении диамагнетика в магнитное
поле происходит поворот орбит электронов так,
что возникшие магнитные моменты
ориентируются против поля (в соответствии с
правилом Ленца). Результирующее магнитное
поле в диамагнетиках ослабляется.
Диамагнетиками являются Cu, Ag, Au, Pb,
инертные газы, многие органические вещества.
50
51.
Молекулы парамагнетиков имеют отличныеот нуля собственные магнитные моменты, которые
без внешнего магнитного поля ориентированы
хаотично.
Во внешнем магнитном поле эти магнитные
моменты стремятся повернуться по полю в той
степени, насколько им это позволяет тепловое
движение. Результирующее магнитное поле в
парамагнетиках незначительно усиливается.
В парамагнетиках наблюдается и
диамагнитный эффект, но он мал по сравнению с
парамагнитным.
К парамагнетикам относятся Na, Mg, R, Ca, Al,
Pt, O2.
51
52.
.Величина магнитной индукции B
испытывает скачок на границе раздела сред.
Характеристикой, которая зависит только
от источников внешнего поля и одинакова для
любой среды, является вектор
напряженности магнитного поля
H
B
o
J
52
53.
.Величина намагниченности пропорциональна Н
J H
где - магнитная восприимчивость, которая наряду с
намагниченностью учитывает влияние среды.
B o ( 1 )H
Величина
1
называется магнитной проницаемостью.
B o H
Напряженность магнитного поля H - это
характеристика источника магнитного поля,
которым являются макротоки.
53
54.
Вспомним, что для вакуума закон полного токаn
охв .
(
B
d
l
)
I
o i
L
i 1
где суммируются все токи, охватываемые замкнутым контуром L.
Причем эти макротоки являются источником магнитного поля.
В магнетике магнитное поле создается как макротоками
(токами проводимости), так и микротоками (орбитальными
токами). Поэтому можно записать
( B dl ) o ( I пров I микро )
охв .
L
I пров - сумма токов проводимости, охватываемых контуром L;
I микро - суммарный микроток через поверхность, ограниченную
контуром L.
54
55.
Циркуляция вектора напряженности магнитногополя вдоль произвольного замкнутого контура
равна алгебраической сумме токов проводимости,
охватываемых данным контуром:
n
( H dl )
L
i 1
охв.
I пров.
Это выражение получено с учетом, что
I микро ( J dl )
L
55
56. Ток смещения
Источником магнитного поля вможет быть не только ток проводимости,
но и изменяющееся с течением времени
электрическое поле.
Максвелл предположил, что в
этом случае возникает так называемый
ток смещения, который пропорционален
скорости изменения индукции
электрического поля:
I см
D
dS
S t
Току смещения соответствует «свое» переменное магнитное поле.
56
57. Закон полного тока для магнитного поля в веществе:
Циркуляция вектора напряженности магнитногополя вдоль произвольного замкнутого контура
равна полному току через поверхность,
ограниченную этим контуром:
(H dl ) I
L
Полный ток
пров
I
I
полн .
смещ
I
пров
I
I
пров
D
dS
t
S
смещ
57
58. Сегнетоэлектричество и ферромагнетизм
Особенности поведения в полеБольшие значения диэлектрической
или магнитной проницаемости.
Например, для титаната бария ~ 104,
для железа = 5000.
Нелинейный характер зависимости
диэлектрической или магнитной
проницаемости от напряженности поля.
Наличие гистерезиса, т.е. зависимости
поляризованности или намагниченности
от предыстории образца.
58
59.
Доменная структура этих веществ: существуютмакроскопические области, в пределах которых
наблюдается одинаковая спонтанная ориентация
дипольных или магнитных моментов молекул
вещества.
Поляризация или намагничивание во внешнем поле
заключается:
- в смещении границ доменов и росте размеров
тех доменов, моменты которых близки по
направлению к направлению внешнего поля;
- в повороте моментов доменов по полю.
Наличие так называемой точки Кюри – критической
температуры, выше которой сегнетоэлектрические
или ферромагнитные свойства исчезают, и вещество
переходит в полярный диэлектрик или парамагнетик.
Например, для железа ферромагнитные свойства
исчезают при температуре Т = 768 С.
59
60. Уравнения Максвелла
Д. Максвелл обобщилосновные законы
электричества и магнетизма и
создал цельную теорию
единого электромагнитного
поля. В этой теории решается
основная задача
электродинамики – расчет
электромагнитного поля
заданной системы
электрических зарядов и
токов. В основе теории
лежат четыре уравнения.
Джеймс Клерк Максвелл
1831–1879
60
61.
Первое уравнение МаксвеллаB
E dl t dS
L
S
Это обобщение закона Фарадея для
электромагнитной индукции. При этом под вектором Е
понимается векторная сумма напряженностей
вихревого и электростатического полей.
Если в некоторой области пространства
происходит изменение магнитного поля, то это
приводит к появлению в этой же области
изменяющегося вихревого электрического поля.
61
62.
Второе уравнение МаксвеллаD
H dl I пров t dS
L
S
Это уравнение есть обобщенный закон
полного тока.
Магнитное поле создают как проводники с
током, так и изменяющееся электрическое поле. Т.е.
переменные электрические и магнитные поля
порождают друг друга.
62
63.
Третье и четвертое уравненияМаксвелла
Первые два уравнения Максвелл дополнил
теоремой Гаусса для векторов D и B
электромагнитного поля:
D dS
S
n
своб
qi
i 1
B dS 0
S
63
64.
Если электромагнитные явления происходятне в вакууме, а в среде, то свойства среды
учитываются ее макроскопическими
характеристиками : диэлектрической
проницаемостью , магнитной проницаемостью
и удельной электропроводностью и система
четырех уравнений дополняется материальными
уравнениями:
D 0 E , B 0 H ,
j
j E
- плотность макротока проводимости..
Теория
Максвелла
позволяет
по
известному
распределению зарядов и токов в среде определить
характеристики
создаваемых
ими
электрического
и
магнитного полей.
64































































 Физика
Физика








