Похожие презентации:
Специальные вопросы гидравлики, водопроводных и водоотводящих сооружений. Гидравлический прыжок. Сопряжение бьефов. (Лекция 3)
1.
Министерство образования и науки УкраиныХарьковский национальный университет городского хозяйства
имени А.Н. Бекетова
Преподаватель: доц. Шевченко Тамара Александровна
Харьков - 2014
2.
Гидравлическим прыжком называется резкое возрастание глубины потока спереходом от бурного до спокойного состояния на относительно небольшой длине
русла.
Гидравлический
Спокойный поток
До прыжка глубина h1 < hк Бурный
поток
прыжок
3
(hк – критическая глубина), а в
2 C
конце прыжка глубина потока h2
> hк (рис. 3.1).
D
Экспериментальными
а
исследованиями выявлено, что в
K
K
гидравлическом прыжке можно
h2
hн
выделить 2 зоны (рис. 3.1):
А
1. Основная струя;
B
hK
2. Поверхностный
вихрь
1
h1
(водоворот).
Линия разграничения этих
2
3
двух частей АВС – это
lc
lп.cт.
1
усредненная во времени линия,
LДСБ
которая
условно
отсекает
основный поток с расходом Q от
поверхностного водоворота.
3.
Глубины h1 и h2 до и после гидравлического прыжка называютсявзаимными или сопряжёнными глубинами, а их разность (h2-h1) определяет
высоту гидравлического прыжка.
Длина L участка, на котором происходит резкое изменение глубин
потока, называется длиной гидравлического прыжка.
Обычно гидравлический прыжок возникает при протекании воды через
возвышение на дне русла, при вытекании из-под щита или перетекании через
водослив.
Основная задача при расчёте гидравлического прыжка:
- определение взаимных глубин,
- длины гидравлического прыжка,
- сопровождающих гидравлический прыжок потерь энергии.
Взаимные глубины определяются соотношением:
где
Fr - число Фруда,
g - ускорение силы тяжести.
Длина гидравлического прыжка определяется по эмпирическим формулам,
например, для прямоугольных русел по формуле H. H. Павловского:
L=2,5 (1,9 h2 - h1).
4.
Потери энергии в гидравлическом прыжке в этом случае.
При больших числах Фруда (Fr>2,5) эти потери составляют свыше 50%, т. е.
гидравлический прыжок - хороший гаситель энергии. Поэтому гидравлический прыжок
используется в гидротехнике, например для защиты от размывов нижнего бьефа
плотин. Так, если истечение воды через гидротехническое сооружение происходит с
образованием отогнанного гидравлического прыжка, т. е. отодвинутого на некоторое
расстояние от сооружения, то во избежание размывов дна ниже сооружения устраивают
водобойные колодцы, стенки, чтобы приблизить гидравлический прыжок к
сооружению (т. е. превратить его в затопленный).
Вдоль гидравлического прыжка изменяется эпюра скоростей. На рис. 3.1
изображены схемы эпюр усредненных скоростей в сечениях:
в начале прыжка (где глубина h1),
в середине длины прыжка
и в конце прыжка (де глубина потока h2).
Как видно из рис. 3.1 в конце прыжка усредненные скорости (точка С) равны
нулю, а возле дна они максимальны. Трансформация эпюр скоростей продолжается
на некоторой длине lп.cт. (до сечения 3-3), которая называется длиной
послепрыжкового участка. За сечением 3-3 вниз по течению эпюры скоростей
отвечают распределению скоростей при равномерном или неравномерном
движении.
Если глубина вдоль потока в нижнем бьефе за сечением
3-3 hн = const, то эпюра скоростей является постоянной.
5.
Длина трансформации эпюр скоростей между сечениями 1-1 и 3-3 называетсяучастком сопряжения бьефов, который в общем случае равен:
LДСБ lС lПСТ lС (10...30)hН
где: lС – длина гидравлического прыжка;
lПСТ – длина послепрыжкового участка;
hн – глубина потока в нижнем бьефе.
Сопряженные глубины совершенного гидравлического прыжка в призматических
руслах с любой формой поперечного сечения можно определить с помощью графика
прыжковой функции (рис. 3.2).
Q
y П ( h)
g
h
2
c
где: ω – площадь живого сечения
потока с глубиной h,
уС
–
глубина
погружения
геометрического центра площади ω.
Функция
П(h)
называется
прыжковой функцией.
h2
hк
h1
0
П (h1) = П (h2)
П (h)
6.
Длину совершенного гидравлического прыжка в прямоугольном русле при b = const иуклоне дна і = 0 можно определить по формулам:
М.Д. Чертоусова
С.К. Кузнецова
А.Н. Айвазяна
lC 10,3h1
Fr1 1
0 , 81
lC 16,7 hK h1
8 (10 Fr1 ) (h2 h1 ) 3
lC
Fr1
4h1 h2
где: h1, h2 – первая и вторая сопряженные глубины прыжка;
Fr1 – число Фруда, которое посчитано по формуле
Fr1
V
1
gh1
1
2
3
7.
Длину гидравлического прыжка в прямоугольном расширяющемся русле можноопределить по формуле А.Ф. Васильева
где lС – длина прыжка в
;
прямоугольном русле при
lC
lC P
lC
2
1
0
,
052
Q
Fr1 3
r
gh1 r
где:
r b1 2 sin
2
b1 – ширина дна при глубине h1;
57,3
0
- угол расширения, рад.
При углах расширения β < 150 имеем βr ≈ b1. Тогда
hK 1
Q
Fr1 2 3
gb1 h1 h1
2
3
8.
Длину прыжка в трапециевидном русле с постоянной шириной дна можноопределить по формуле С. Мейерова
m(h2 h1 )
lПТ lс 1 1,76
1
где: lС – длина прыжка в прямоугольном русле;
χ1 – смоченный периметр в сечении с глубиной h1;
m – коэффициент заложения откосов канала.
Длину прыжка в руслах с уклоном дна і > ік приближенно можно определить по
формуле
lCT lC (1 k i)
где: lС – длина прыжка при і = 0;
k – коэффициент увеличения длины прыжка при і > 0.
По данным Г.М. Косяковой k = 3, а по данным Г.К. Илчева k = 3,75.
Глубину под гребнем первой волны в прямоугольном русле при b = const
приблизительно можно определить по формуле С.К. Кузнецова
lCX 13,4(hK h1 )
9.
Если число Fr1 = (1,5…3), то наибольшую глубину волнового прыжка hволн можноопределить по формуле М.С. Краснитского
h
BОЛН
h 1 0,72 Fr 1
1
1
Соотношение между сопряженными глубинами волнового прыжка
По исследованиям А.А. Рябенко можно определить по формуле
1
2 2 1 Fr1
3
2
2 h2 h1
Fr1 3 2 1 Fr1 1
2
1
По исследованиям А.А. Рябенко при числах Fr1 > 2 можно принимать, что β1 = 1, а
при Fr1 = (1,1…1,5) - β1max = 1,045.
В случае, когда β1 = 1, то
1
h2 h1 (1 Fr1 )
3
hXB h1 Fr1
10.
α0V01
2/2g
hw(1-C)
Н0
Н
Т0
αCVC2/2g
Т
PH
Для определения глубины hС в
нижнем
бьефе
сооружений
используем уравнение Бернулли,
которое запишем для сечений 1-1 и
С-С
относительно
плоскости
сравнения 0-0
Допустим, что в живых сечениях
1-1 и С-С
движение
плавно
изменяющееся и пьезометрические
напоры равны:
hC
1
0
0
С
Тогда уравнение Бернулли относительно плоскости 0-0
приобретает вид:
T
0V02
2g
hC
CVC2
2g
hW (1 C )
P1
T;
g
P
z 2 2 hC .
g
Н П 1 z1
С
НП2
VC2
T0 hC
( c )
2g
11.
где: Т0 – полная удельная энергия потока в сечении 1-1Т0 T
0V02
2g
V0 – средняя скорость потока в сечении 1-1;
VС = Q / ωС - средняя скорость потока в сечении С-С;
ωС – площадь живого сечения потока при глубине hC;
ξ – коэффициент гидравлических сопротивлений между сечениями 1-1 та С-С.
Из уравнения:
2
V
T h
( ) VC
2g
C
0
C
c
где φС – коэффициент скорости
С
C 2 g (T0 hC )
1
С
Величина коэффициента φС зависит от типа и геометрических размеров сооружения и
гидравлических параметров потока.
Учитывая, что V Q
C
C
Q C C 2 g T0 hC
Это общее уравнение для определения глубины hС в
стесненном сечении в нижнем бьефе
гидротехнического сооружения.
12.
аб
в
г
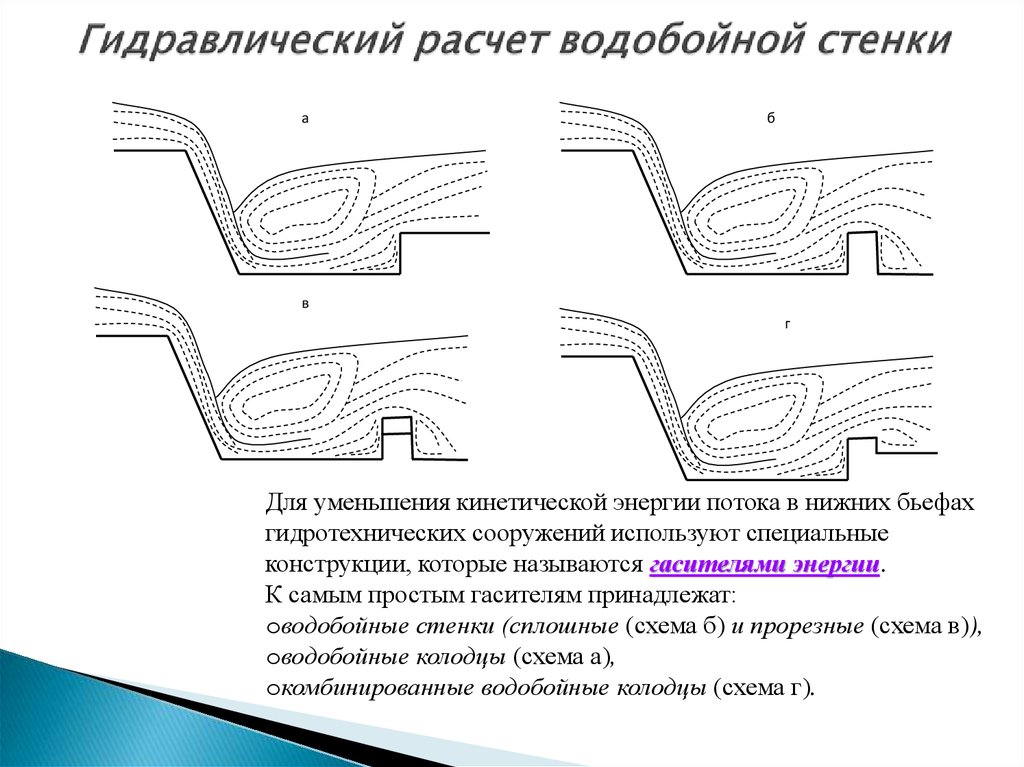
Для уменьшения кинетической энергии потока в нижних бьефах
гидротехнических сооружений используют специальные
конструкции, которые называются гасителями энергии.
К самым простым гасителям принадлежат:
oводобойные стенки (сплошные (схема б) и прорезные (схема в)),
oводобойные колодцы (схема а),
oкомбинированные водобойные колодцы (схема г).
13.
Для определения высоты водобойной стенки допускают, что она работает какнекоторый водослив. Соответственно высота стенки:
C 3 h2 H C
где: σ3 = 1,05…1,1 – коэффициент затопления гидравлического прыжка;
h2 – вторая сопряженная глубина прыжка при расходе Qр;
Нс – напор над водобойной стенкой, который определяют по формуле:
Qp
HC
m B 2g
п c CT
2
3
где:
ВСТ – длина стенки;
σп = f (hп / Нс) – коэффициент подтопления водобойной стенки со стороны нижнего бьефа;
hп – глубина подтопления стенки
hп hн С
mс – коэффициент расхода водобойной стенки как водослива. Он зависит от типа
водобойной стенки (сплошная, прорезная) и ее размеров и напора Нс.
14.
Так как перед началом расчетов неизвестно:водобойная стенка подтопленная или неподтопленная,
соответственно неизвестно значение и коэффициента подтопления стенки σп;
неизвестно также значение коэффициента расхода mс, потому что mс = f (С, Нс).
В этом случае высоту водобойной стенки можно определить графоаналитическим
способом. Ход расчетов может быть таким:
задаются несколькими значениями высоты стенки С;
рассчитывают величины Нс, hп, mс, σп и определяют расходы.
3
Q п mc BCT 2 g H c 2
Результаты расчетов целесообразно сводить в следующую таблицу:
С H h C h h С
σп
mс
Q
С1
Q1 < Qр
С2
Q2
С3
Q3 > Qр
По данным этой таблицы строят график С = f (Q), с помощью которого
С
определяют высоту стенки С.
C
3
2
п
н
Ср
Qр
Q
15.
Расстояние до водобойной стенки от сечения с глубиной h1 определяют по формулеl K lC
где: lС – длина гидравлического прыжка;
β = 0,7…0,9 – коэффициент уменьшения гидравлического прыжка.
Если водобойная стенка высокая, то за ней может образоваться отогнанный гидравлический
прыжок. Возможность образования этого явления проверяют таким образом: используя
следующую формулу определяют сжатую глубину за стенкой:
где:
φС – коэффициент скорости,
Q
который учитывает потери энергии при
hC1
переливе потоку через водобойную стенку;
C BCT 2 g T0C hC1
Т0С – полная удельная энергия потоку
относительно дна нижнего бьефа за стенкой
T0C 3 h2
Q
2
p
2 g BCT 3 h2
2
где:
α = 1,1…1,2 – коэффициент
кинетической энергии потока в сечении с
глубиной h = σ3h2;
ВСТ – длина водобойной стенки.
Принимая, что первая сопряженная глубина прыжка h1 = hС2, по
уравнением гидравлического прыжка определяют вторую сопряженную глубину
прыжка h2. Если h2 > hн, то за стенкой прыжок отогнанный и необходимо
запроектировать другую водобойную стенку или вместо водобойных стенок
взять другой гаситель энергии, например, водобойный колодец или
комбинированный водобойный колодец..
16.
17.
αV02/2ga
H
T0C 3 h2
T0
T
Q p2
2 g BCT 3 h2
2
z
σ3 h2
hH
d
lk
h1 = hc
αV02/2g
б
H
T0
d
R hЦУ У h2 0 d 0
2
T
h1 = hc
R
P1
lk
P2
d0
В результате гидравлических расчетов необходимо
определить глубину колодца d и его длину lк
18.
Глубину водобойного колодца можно определить несколькими способами:1) Принимают, что выход из водобойного колодца работает как затопленный водослив с
широким порогом (рис. а).
Исходя из того, что колодец должен образовать глубину воды для затопления прыжка, в
соответствии со схемой рис. а, глубину колодца можно определить по формуле
d 3 h2 hH z
где: σ3 =1,05…1,1 – коэффициент затопления прыжка;
h2 – вторая сопряженная глубина прыжка при расчетном расходе Qр;
hн – глубина воды в нижнем бьефе при расходе Qр;
Z – гидравлический перепад, для определения которого используют формулу пропускной
способности водослива с широким порогом, т.е.
где: φп
=
0,98…0,99
–
2
2
Q p
коэффициент скорости;
1 Qp
z z0
z0
2 Вк – ширина водобойного колодца в
2 g п Вк hн
2 g 3 h2 BK плоскости
вертикального уступа.
Т.к., при устройстве водобойного колодца потенциальная энергия потока верхнего бьефа
увеличивается на величину d, то глубина потока в сечении С-С несколько уменьшится, а вторая
сопряженная глубина прыжка немного увеличится. Поэтому необходимо выполнить уточнение
глубины колодца. Для этого по следующей формуле уточняют глубину в сжатом сечении С-С:
Принимая, что h1 = hС1, по формуле
q
сопряженных глубин определяют новое
hc1
значение h2 и рассчитывают глубину
c 2 g T01 hc1
водобойного
колодца
во
втором
приближении. Как правило третьего
приближения не выполняют.
19.
2) Для определения глубины колодца, которая образует придвинутый к сечению С-Сгидравлический прыжок, составим уравнение изменения количества движения в потоке между
сечениями с глубинами hС и hН в проекциях на горизонтальную ось:
0 Q(V2 V1 ) P1 P2 R
где: R – реакция водобойного уступа, высота которого равна d0 (рис. б);
Р1, Р2 – силы гидродинамического давления в сечениях 1-1, 2-2. Приняв, что Р1 и Р2 можно
определить по законам гидростатики, т.е.:
hH
hH2
P2 gyC 2 2 g
hH B g
B
2
2
hC
hC2
P1 gyC1 1 g
hC B g
B
2
2
Подставив значения и разделив все члены уравнения на ρgB. Тогда получим
0Q 2 1
1
gB 2 hH hC
hC2 hH2 R
2
2
Допустим, что корректирующий коэффициент количества движения α0 равен корректирующему
коэффициенту кинетической энергии α. Тогда выражение
2
2
3
Q
gB
h
0
K
где hК – критическая глубина в прямоугольном
русле.
Уравнение пишем в таком виде:
2
hK3 hC hK3 hH2 R
hC
2 hH
2
20.
Если длина колодца lК ≥ lС (где lС – длина свободного совершенного прыжка), то реакцию Rможно определить по гидростатическому закону. Тогда, принимая, что перед уступом d0 глубина воды
h = h2, получим
.
R hЦУ
d0
У h2 d 0
2
где: hцу – глубина погружения геометрического центра площади сечения с глубиной h2.
Подставляя значение R в уравнение, получим
Параметр А равен:
d 0 h2 h A
2
2
2hK3
A hH hC
hH hC
hC hH
Для образования затопленного прыжка глубину d0 необходимо увеличить. С учетом
затопления прыжка глубину колодца рассчитывают по такой формуле:
где: σ3 = 1,05…1,1 – коэффициент затопления прыжка;
hН – глубина воды в нижнем бьефе при расчетном
3 0
3
H
расходе Qр.
d d 1 h
Длину колодца можно назначать в пределах:
l K lC (0,8...1,0)lC



















 Промышленность
Промышленность








