Похожие презентации:
Алгебра логики
1. Алгебра логики
АЛГЕБРА ЛОГИКИ2. Конъюнкция (или логическое умножение)
КОНЪЮНКЦИЯ (ИЛИ ЛОГИЧЕСКОЕУМНОЖЕНИЕ)
Конъюнкция - это сложное логическое выражение,
которое считается истинным в том и только том
случае, когда оба простых выражения являются
истинными, во всех остальных случаях данное
сложенное выражение ложно.
Обозначение: F=A˄B
Таблица истинности для конъюнкция
А
В
F
1
1
1
1
0
0
0
1
0
0
0
0
3. Дизъюнкция (или логическое сложение)
ДИЗЪЮНКЦИЯ (ИЛИ ЛОГИЧЕСКОЕСЛОЖЕНИЕ)
Дизъюнкция - это сложное логическое выражение,
которое истинно, если хотя бы одно из простых
логических выражений истинно и ложно тогда и
только тогда, когда оба простых логических
выражений ложны.
Обозначение: F = A ˅ B
Таблица истинности для дизъюнкции
А
В
F
1
1
1
1
0
1
0
1
1
0
0
0
4. Инверсия ( или логическое отрицаяние)
ИНВЕРСИЯ ( ИЛИ ЛОГИЧЕСКОЕОТРИЦАЯНИЕ)
Инверсия - это сложное логическое выражение,
если исходное логическое выражение истинно, то
результат отрицания будет ложным, и наоборот,
если исходное логическое выражение ложно, то
результат отрицания будет истинным. Другими
простыми слова, данная операция означает, что к
исходному логическому выражению добавляется
частица НЕ или слова НЕВЕРНО, ЧТО.
Таблица истинности для инверсии
А
ഥ
А
1
0
0
1
5. Импликация (или логическое следование)
ИМПЛИКАЦИЯ (ИЛИ ЛОГИЧЕСКОЕСЛЕДОВАНИЕ)
Импликация - это сложное логическое выражение,
которое истинно во всех случаях, кроме как из
истины следует ложь. То есть данная логическая
операция связывает два простых логических
выражения, из которых первое является условием
(А), а второе (В) является следствием.
Таблица истинности для импликации
А
В
F
1
1
1
1
0
0
0
1
1
0
0
1
6. Порядок выполнения логических операций в сложном логическом выражении
ПОРЯДОК ВЫПОЛНЕНИЯЛОГИЧЕСКИХ ОПЕРАЦИЙ В СЛОЖНОМ
ЛОГИЧЕСКОМ ВЫРАЖЕНИИ
1. Инверсия;
2. Конъюнкция;
3. Дизъюнкция;
4. Импликация.
!!!Для изменения указанного порядка выполнения
логических операций используются скобки.
7.
Выразите следующие высказывания на языкеалгебры логики. Пусть:
a = “это утро ясное”,
b = “это утро теплое”.
а) “это утро ясное и тёплое”;
б) “это утро ясное и оно не тёплое”;
в) “это утро не ясное и оно не тёплое”;
8. Примеры!
ПРИМЕРЫ!Заполните таблицу истинности для функции:
F=A˅B
A
0
0
1
1
B
0
1
0
1
F
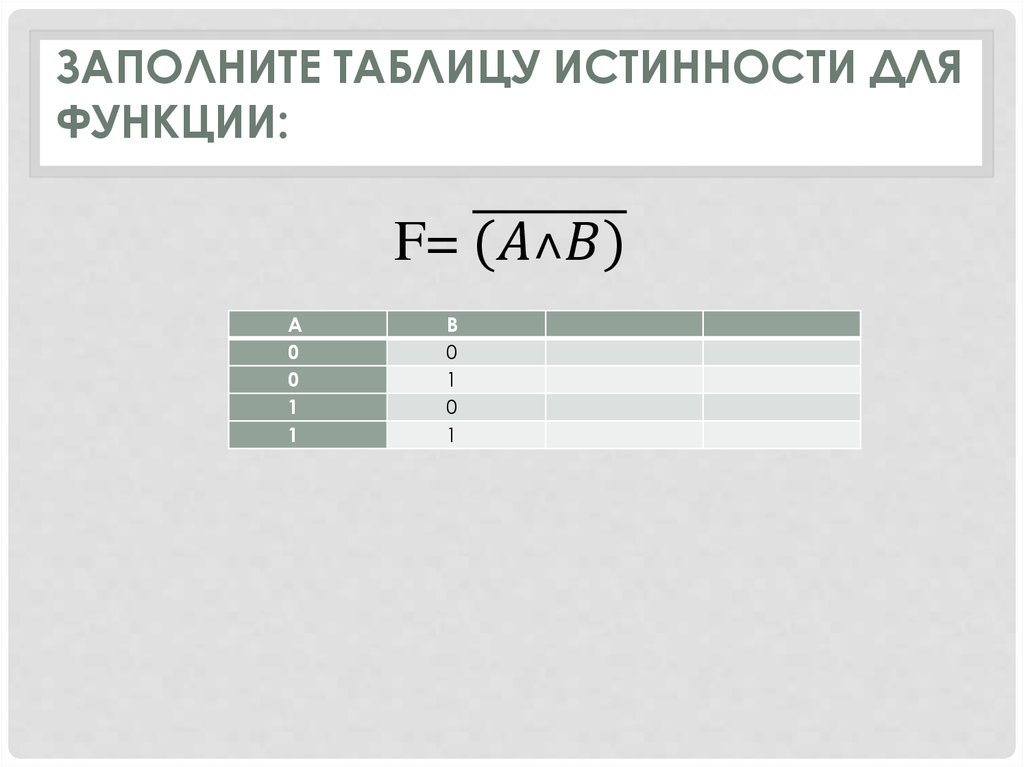
9. Заполните таблицу истинности для функции:
ЗАПОЛНИТЕ ТАБЛИЦУ ИСТИННОСТИ ДЛЯФУНКЦИИ:
F= (








 Информатика
Информатика








