Похожие презентации:
Тепломассообмен в адсорбционных процессах. Основные понятия и определения
1. Лекция 21. Тепломассообмен в адсорбционных процессах
ЛЕКЦИЯ 21. ТЕПЛОМАССООБМЕН В АДСОРБЦИОННЫХ ПРОЦЕССАХОсновные понятия и определения
Адсорбция – явление концентрирования вещества из объема фаз на
поверхности раздела фаз или в объеме пор твердого тела; процесс
массопередачи путем адсорбции.
Адсорбтив – поглощаемое вещество в неадсорбированном состоянии.
Адсорбат – поглощаемое вещество, перешедшее в адсорбированное
состояние.
Адсорбент – тело на поверхности или в объеме пор которого
происходит концентрирование поглощаемого вещества.
Истинная плотность
адсорбента без пор.
Кажущаяся плотность
пористого адсорбента
адсорбента
адсорбента
–
–
масса
масса
единицы
объема
единицы
объема
Насыпная плотность адсорбента – масса единицы объема
адсорбента, включая объем пор и промежутков между гранулами
адсорбента.
2.
Основные понятия и определенияПоры адсорбента – полости между элементами структуры адсорбента.
Открытые поры – являются проницаемыми и сообщаются с
поверхностями пористого тела.
Закрытые поры – не сообщаются с другими поверхностями
пористого тела и являются непроницаемыми.
Тупиковые поры (полуоткрытые или полузакрытые) – образуют
тупиковую пористость могут заполняться жидкостью или газом, но не
являются проницаемыми.
Пористость (П) – отношение объема пустот (Vп) в материале к его
полному объему (V).
П=Vп/V;
П=(mн – m)/(ρжV);
П=1 – ρ/ρк
где mн, m – масса насыщенного жидкостью материала и материала, кг; ρж, ρ
и ρк – плотности жидкости, пористого и компактного материала, кг/м3.
Просвет (Ф) – доля площади
приходящаяся на пустоты.
сечения
пористого
материала,
Замечание: Величины просвета и пористости не равны между собой, а
расхождение в их значениях зависит от вида пористого материала
(исключение составляют материалы с изотропной структурой, в которых
этих величины совпадают)
Справочно: П=k1Ф1,4 (справедлива для пористого тела из сфер)
3.
Основные понятия и определенияХемосрбция – адсорбция, сопровождающаяся химическим
взаимодействием между молекулами адсорбата и адсорбента.
Адсорбция физическая – адсорбция, вызванная силами
молекулярного взаимодействия адсорбента с адсорбтивом.
Монослойная
(мономолекулярная)
–
сопровождающаяся
образованием
на
поверхности
адсорбента единственного слоя молекул адсорбата.
Полислойная (полимолекулярная) – в ходе которой на
поверхности адсорбента образуется два или большее число
слоев молекул адсорбата.
Селективная (избирательная) – при которой из смеси
веществ адсорбируется один или несколько ее компонентов.
Необратимая – хемосорбция, осуществляющаяся за счет
необратимых химических реакций.
Фронт адсорбции – распределение концентраций в любой из
фаз, достигнутое к некоторому моменту времени.
4.
Основные понятия и определенияОсновные виды сил:
Движущая сила – разность значений интенсивной
определяющей направление процесса переноса.
характеристики,
Движущая сила массопередачи – движущая сила массообмена, вызванная
разностью равновесных и рабочих концентраций в одной из участвующих в
процессе фаз.
Средняя движущая сила массопередачи – движущая сила масоопередачи
усредненная по всей поверхности контакта фаз.
Движущая сила теплопередачи – разность средних температур
теплоносителей в определенном сечении аппарата
Средняя движущая сила теплопередачи – выраженная разностью
температур теплоносителей по всей поверхности теплопередачи.
Адсорбционные силы:
Дисперсионные – универсальные неспецифические силы молекулярного
взаимодейстия, не зависящие от взаимодействия адсорбтива и адсорбента
Электростатические силы – специфические силы, зависящие от
химической природы адсорбтива и адсорбента.
Ориентационные – возникающие при взаимодействии полярных
молекул с поверхностью, содержащей электростатические заряды (ионы,
диполи).
Индукционные – вызываются изменением электронной структуры
молекул адорбтива и адсорбента под действием друг друга
5.
Основные виды пор адсорбентовМикропоры – наиболее мелкие поры, имеющие размеры
соизмеримые
с
адсорбируемыми
молекулами,
с
эффективном размером пор 0,5-1,0 нм. с верхней границей
1,5 нм и суммарным объемом не более 0,5 см3/г.
Замечание: Иногда наиболее крупные микропоры
размером от 0,7 до 1,5 нм. выделяют в отдельную категорию
супермикропоры. В них адсорбция может протекать по
механизму покрытия поверхности одним или даже
несколькими слоями молекул адсорбата.
Мезопоры – поры с эффективным размером пор от 1,5 до
100-200
нм,
существенно
превышающем
размеры
адсорбируемых молекул.
Замечание: Здесь происходит мономолекулярная и
полимолекулярная адсорбция, а мезопоры выполняют роль
транспортных каналов, по которым осуществляется подвод
вещества к микропорам.
Макропоры – поры с эффективным размером больше 100200 нм. Их удельная поверхность очень мала – от 0,5 до
2 м2/г, вследствие чего адсорбцией на поверхности пор этого
типа можно практически пренебречь.
6.
ОСНОВНЫЕТИПЫ ИЗОТЕРМ АДСОРБЦИИ
Внимание! Соотношение между микро-, мезо- и макропорами
адсорбента во многом определяет вид изотермы адсорбции
[a=f(p) при
T=const] удаляемых веществ на выбранном
адсорбенте, которая выступает в качестве
основной
характеристики адсорбционной способности адсорбента
и определяет выбор оптимальных рабочих условий
процесса.
Классификация Брунауэра, Эмита и Тейлора (БЭТ)
Классификация Международного союза по чистой и прикладной химии (ИЮПАК)
7.
ОСНОВНЫЕ ТИПЫ ИЗОТЕРМ АДСОРБЦИИ СОГЛАСНО КЛАССИФИКАЦИИБРУНАУЭРА, ЭМИТА И ТЕЙЛОРА (БЭТ)
I тип – характерен для микропористых адсорбентов,
практически не содержащих мезопор. Отличительной
особенностью этого типа изотерм является наличие
горизонтального участка, обусловленного следующим:
размеры пор настолько малы, что на их стенках не
может образовываться более одного слоя молекул.
Таким образом горизонтальный участок соответствует
завершению образования монослоя.
II и IV тип – характерен для пористой структуры
мезопористых твердых тел. Особенностью этих типов
изотерм адсорбции является наличие точки перегиба
«А», свидетельствующей о завершении образования
монослоя (начальный выпуклый участок) и переходе к
полимолекулярной адсорбции.
Наличие верхнего почти горизонтального участка на
изотерме
адсорбции
IV
типа
соответствует
капиллярной конденсации.
III и V тип – встречается довольно редко и имеют
вблизи от начала координат вогнутый участок. Они
характерны для слабого взаимодействия системы
адсорбент-адсорбат, когда взаимодействие молекул
адсорбата с адсорбентом меньше межмолекулярного
взаимодействия для молекул адсорбата.
Вывод: Указанные особенности изотерм адсорбции
необходимо учитывать для обоснованного выбора
соответствующего адсорбента.
8.
ОСНОВНЫЕВИДЫ ПРОМЫШЛЕННЫХ АДСОРБЕНТОВ
Силикагель – минеральный адсорбент
Размер зерна, мм
Объем пор, см3/г
Удельная поверхность, м2/г
Средний радиус пор, нм
Истинная плотность, г/см3
Кажущаяся плотность, г/см3
Насыпная плотность, г/см3
Теплоемкость, кДж/кг.К
Теплопроводность, кДж/м.ч.К
Количественные
значения
0,1-7,0
0,3-1,2
300-750
1,0-7,0
2,1-2,3
0,4-1,7
(0,1)0,4-0,9
~ 0,92
~ 0,71
Теплота адсорбции паров воды, кДж/кг
~ 2600
Характеристика
Мелкопористый
Крупнопористый
Основное преимущество силикагелей – низкая температура термической
регенерации (110-180 оС) и более низкие энергозатраты. Кроме того, данный
тип промышленных адсорбентов допускает применение безнагревных методов
его регенерации.
Цеолиты (молекулярные сита) – синтетический адсорбент
Характеристика
Размер зерна, мм
Объем пор, см3/г
Удельная поверхность, м2/г
Средний радиус пор, нм
Кажущаяся плотность, г/см3
Насыпная плотность, г/см3
Теплоемкость, кДж/кг.К
Теплопроводность, кДж/м.ч.К
Количественные
значения
1-5
0,4-0,67(1,0)
90-400
5,0-11,0
1,0-2,0
0,62-0,78
~ 0,83-1,0
~ 0,5-0,67(2,1)
Тип А
Тип Х
9.
ОСНОВНЫЕАлюмогель
адсорбент.
ВИДЫ ПРОМЫШЛЕННЫХ АДСОРБЕНТОВ
(активный
Характеристика
Размер зерна, мм
Объем пор, см3/г
Удельная поверхность, м2/г
Средний радиус пор, нм
Истинная плотность, г/см3
Кажущаяся плотность, г/см3
Насыпная плотность, г/см3
оксид
алюминия)
Количественные
значения
3-4
(0,15)0,4-0,7
170-220
3-4
3,25-3,5
1,6
(0,35)0,6-0,9
–
неорганический
Допускает
применение
термических
методов
регенерации, так же как и
цеолиты, при температуре
от 270-600 оС.
Активные (активированные) угли – состоят в основном из углерода.
Структура угля представлена
Количественные
Характеристика
значения
гаммой пор всех размеров,
причем
адсорбционная
Размер зерна, мм
0,15-5
емкость и скорость адсорбции
Объем пор, см3/г
0,67-1,0
3
компонентов промышленных
Истинная плотность, г/см
1,8-2,2
газов
определяются
Кажущаяся плотность, г/см3
0,4-1,0
содержанием микропор в
Насыпная плотность, г/см3
0,2-0,6
.
единице массы или объема
Теплоемкость, кДж/кг К
~ 0,84
гранул.
Теплопроводность (при 30 оС), Вт/м.К
~ 0,17-0,28
Внимание! При выборе типа адсорбента следует учитывать два
отличительных свойства активных углей – гидрофобность и горючесть.
Активный уголь – единственный гидрофобный тип промышленных
адсорбентов, что предопределило его широкое использование для
рекуперации паров, очистки влажных газов и сточных вод.
10.
Изотермы адсорбции паров воды на различныхпромышленных адсорбентах
а, % (по массе)
60
Активные угли
50
Активный глинозем
40
Алюмогель
30
Цеолиты
Крупнопористый
силикагель
Среднепористый
силикагель
Мелкопористый
силикагель
20
10
0
0
0,1
0,2
0,3
0,4
0,5
0,6
0,7
0,8
0,9
Р/Р1s
Выбор конкретного вида промышленного адсорбента определяет:
Уровень осушки/очистки/разделения исходной смеси (газ,
содержащий ценный компонент; непосредственно ценный газ;
воздух).
Динамическую активность адсорбента.
Условия регенерации адсорбента.
Механическую прочность адсорбента, деградацию и т.п.
11. Характеристика методов адсорбционной осушки воздуха по данным фирмы “DSD Dillinger Stahlban GmbH”
Тип блока осушкиНеобходимая
мощность,
кВт*ч
Стоимость
энергии,
у.е.
Потери
воздуха,
м3/ч
Стоимость
потерь
воздуха, у.е.
Затраты на
средства
осушки, у.е.
Сумма затрат на
осуществление
процесса, у.е.
Блок короткоцикловой
осушки
0,1
0,01
240
2,64
0,23
2,88
Блок осушки с
термической
регенерацией
сорбента
18
1,98
40
0,44
0,38
2,8
Блок короткоцикловой
осушки с
энергосберегающим
устройством
0,1
0,01
112
1,23
0,23
1,47
1.
2.
3.
Пределы производительности короткоцикловых установок очень широки: от 2 до
3800 м3/ч.
Традиционно
считалось,
что
применение
короткоцикловых
блоков
осушки
3
производительностью более 1000 м /ч (при нормальных условиях) нецелесообразно
из-за больших потерь воздуха.
Однако встречаются описания установок подобного типа производительностью
5400 м3/ч (при нормальных условиях).
12.
ЛЕКЦИЯ 22. ДИНАМИКА АДСОРБЦИИ.УРАВНЕНИЕ МАТЕРИАЛЬНОГО
БАЛАНСА
Рассмотрим баланс вещества в выделенном
элементарном объеме. Пусть х координата
соответствующая направлению перемещения
потока со скоростью w через элемент
пористого тела с площадью поперечного
сечения dS и толщиной dx.
Количество вещества, входящего в элементарный
объем через площадь dS за время dτ: wc·dS ·dτ
Количество вышедшего вещества:
wc·dS ·dτ + d(wc·dS ·dτ)
Изменение количества вещества в адсорбенте:
a
dS dx d
Изменение количества вещества в подвижной фазе:
c
dS dx d
Общий материальный баланс в элементарном слое:
( wc)
a
c
a c ( wc)
dS dx d
dS dx d
dS dx d или
0
x
x
13.
УРАВНЕНИЕ МАТЕРИАЛЬНОГОБАЛАНСА
Учет изменения концентрации вещества в элементарном
вследствие диффузии приводит к следующему выражению:
объеме
2
a c ( wc )
* c
D
x
x 2
Длительное время считалось, что коэффициент продольной диффузии
может быть рассчитан на основе вычисления коэффициента молекулярной
диффузии (газа или пара).
В настоящее время проявления продольной диффузии при адсорбции
обычно отождествляются с нарушениями поршневой структуры потока в
зернистом слое. При этом считается, что составляющими элементами
продольного переноса являются: флуктуация скорости, неравномерное
распределение потока по сечению аппарата («пристеночный эффект»),
конвекционные перемешивания и молекулярная диффузия.
Замечание: Все эти элементы в основном связаны с гидродинамикой
потока, движущегося непосредственно в зернистом слое и практически не
учитывают неравномерность процессов, происходящих внутри зерна
сорбента, обусловленных его структурой и неравновесностью протекающих
процессов.
14.
УРАВНЕНИЕ КИНЕТИКИ АДСОРБЦИИСкорость адсорбции или количество адсорбируемого из потока вещества в
единицу единицей объема слоя адсорбента, определяется обычно из
уравнения кинетики адсорбции:
da
(с с * )
d
β кинетический коэффициент, 1/с; с – текущая концентрация адсорбтива в
потоке, кг/м3; с* – концентрация адсорбтива на поверхности раздела фаз,
равновесная текущей величине адсорбции.
Таким образом, кинетический коэффициент β показывает, какое количество
вещества (в кг) передается из газового потока 1 м3 слоя адсорбента за 1 с при
разности концентраций 1 кг/м3. β учитывает перенос вещества из потока к
поверхности поглотителя путем молекулярной и конвективной диффузий.
Зависит от геометрических, физических и гидродинамических параметров
процесса.
В твердой фазе конвекция отсутствует, и перемещение вещества вглубь по
порам поглотителя к активной сорбирующей поверхности осуществляется за
счет массопроводности (k):
da
dс
k
d
dx
Замечание: Уравнение кинетики адсорбции – это не что иное, как уравнение
массопередачи, а кинетический коэффициент – коэффициент массоопередачи.
15.
УРАВНЕНИЕ КИНЕТИКИ АДСОРБЦИИУравнение кинетики адсорбции может быть переписано как:
da
K с
d
где ∆с – движущая сила процесса, равная разности между рабочими (с) и
равновесными (ср) концентрациями поглощаемого вещества; K –
коэффициент массопередачи, определяющий количество вещества,
переходящего при заданных условиях из газообразной фазы в твердую.
Таким образом, массопередача в адсорбционных
складывается из следующих процессов:
процессах
1) Внешняя диффузия или диффузия молекул сорбируемого вещества из
потока к внешней поверхности частиц поглотителя через окружающую их
пленку (внешний массообмен);
2) Внутренняя диффузия или диффузия молекул сорбируемого вещества
вглубь по порам поглотителя к его сорбирующей поверхности;
3) Собственно
поглотителя.
сорбция
на
внутренней
сорбирующей
поверхности
Замечание: Полагая, что собственно сорбция происходит весьма быстро,
практически мгновенно, можно считать, что кинетика адсорбции
определяется скоростью диффузии внешней и внутренней.
При
внешнем
массообмене
гидродинамический режим.
существенно
влияет
на
процесс
16.
УРАВНЕНИЕ ТЕПЛОВОГОБАЛАНСА
Уравнение теплового баланса для элементарного объема зернистого слоя
по форме записывается аналогично уравнению материального баланса:
2
a c
c
* c
w D
x
x 2
Для адиабатического процесса тепловой баланс может быть записан
следующим образом:
ha
Ta
T
T (Qa )
hг г whг г
x
где ha, hг – теплоемкость адсорбента и газа; Ta, Tг – температура
адсорбента и газа; Q – тепловой эффект сорбции.
Сопоставление этих уравнений указывает, что в уравнение теплового
баланса не включено слагаемое, соответствующее продольным эффектам.
Замечание: Теплообмен между твердым телом и потоком лимитируется
или внешней теплоотдачей, или теплопроводностью гранул, или
определяется совместно этими двумя механизмами.
17.
УРАВНЕНИЕ ТЕПЛОВОГОБАЛАНСА
В реальных условиях работы зернистых слоев адсорбентов и катализаторов
теплообмен, в отличие от массообмена, практически полностью
определяется теплоотдачей от ядра потока к внешней поверхности частиц
твердого тела.
Распространение тепла по частице проходит достаточно быстро. В этом
случае для «чисто» теплотехнической задачи уравнение передачи тепла
можно записать следующим образом:
ha
T
K г (Т г Т а )
где Кг – объемный коэффициент теплоотдачи; Tг – текущая температура
ядра потока; Tа – текущая температура частиц твердого тела.
Для теплоотдачи, включающей тепловые эффекты адсорбции, изменение
температуры адсорбента описывается уравнением:
ha
T
a
K г (Т г Т а ) Q
18. Модели динамики адсорбции
ЛЕКЦИЯ 23. ДИНАМИКА АДСОРБЦИИ.МОДЕЛИ ДИНАМИКИ АДСОРБЦИИ
Начальные и граничные условия
Принимаются следующие распределения концентрации и температур в
начальный момент времени:
τ = 0;
0 ≤ х ≤ L;
с = 0;
а = 0;
Та = Тг = Тн,
Принятое начальное условие означает, что до начала процесса ни в
газовой, ни в твердой фазах на всем протяжении адсорбера адсорбат не
содержался.
Граничные условия при х=0 формулируются следующим образом:
τ>0;
c=c0=const;
a=a(τ);
Tг = Tг0 = const;
Ta = Ta(τ),
Т.е. в течение всего процесса в слой поступает газовый поток при
постоянной концентрации адсорбтива и температуре.
где Тг – текущая температура ядра потока (газа); Та – текущая
температура частиц твердого тела (адсорбента); Тн – начальная
температура потока, Тг0 – температура ядра потока на входе в слой
сорбента.
19. Модели динамики адсорбции
МОДЕЛИ ДИНАМИКИ АДСОРБЦИИМодели однокомпонентной равновесной изотермической
адсорбции T=const
Процесс при отсутствии продольной диффузии
a c
c
w 0
x
a f (c)
Система имеет два решения:
при наличии конечного градиента концентраций в адсорбере ( с / х а / х
w
Wi
закон Викке
1 f (ci )
при «прямоугольном» («обрывном») фронте сорбции ( с / х а / х )
W
wc0
c0 a0
закон Вильсона
где Wi – скорость движения концентрационной точки i по слою адсорбента;
f’(ci) – производная изотермы адсорбции в точке i; W – скорость движения всех
точек «прямоугольного» фронта; со – концентрация адсорбтива в потоке;
ао – равновесная ей величина адсорбции.
20. Механизм продвижения фронта адсорбции
МЕХАНИЗМ ПРОДВИЖЕНИЯ ФРОНТА АДСОРБЦИИВыпуклый участок изотермы адсорбции.
Согласно закону Викке W1<W2.
Это означает, что первоначально заданное расстояние между точками 1 и 2
уменьшается – точки сближаются.
При «обрывном фронте действие закона Викке прекращается и все точки
распространяются с постоянной скоростью W по закону Вильсона
Вогнутый участок изотермы адсорбции.
Согласно закону Викке W1>W2.
Это означает, что имеет место неограниченное «размывание» фронта.
21. Модели динамики адсорбции
МОДЕЛИ ДИНАМИКИ АДСОРБЦИИДля линейной изотермы (изотермы Генри) при отсутствии
диффузионных эффектов закон Викке совпадает с законом Вильсона, а
скорость перемещения будет равна:
w
Wi
1 f (ci )
1
a c
Независимо от направления движения потока и вида начального
распределения концентрационные точки перемещаются по слою с
постоянной и равной скоростью (W1=W=W2) и любое начальное
распределение сохраняет свою конфигурацию.
Линейный участок изотермы адсорбции
22. Модели динамики адсорбции
МОДЕЛИ ДИНАМИКИ АДСОРБЦИИПроцесс с учетом продольной диффузии
a c
c
2c
w D* 2
x
x
a f (c)
Режим адсорбции при D*≠0 характеризуется тем, что одновременно действуют
два фактора:
Первый фактор – продольная диффузия, которая вызывает размывание
адсорбционного фронта.
Второй фактор связан с законом Викке и, следовательно, с видом изотермы
адсорбции
При вогнутой изотерме адсорбции:
При линейной изотерме адсорбции:
Эффект,
компенсирующий
размывающее
воздействие
продольной диффузии, отсутствует.
Поэтому
режим
параллельного
переноса не устанавливается.
Режим параллельного переноса не
устанавливается.
Система уравнений может быть
решена численными методами.
Из-за отсутствия эффектов сжатия
фронта
его
протяженность
непрерывно увеличивается.
23. Модели динамики адсорбции
МОДЕЛИ ДИНАМИКИ АДСОРБЦИИПри выпуклой изотерме адсорбции:
-
действие закона Викке приведет к сжатию сорбционного фронта;
-
в связи с эффектом продольной диффузии первоначальное «обрывное
распределение начнет размываться.
При наличии двух противоположно действующих эффектов через некоторое
время их действие компенсируется и фронт сорбции начнет перемещаться по
слою с постоянной скоростью в режиме параллельного переноса.
Подобный механизм образования стадии параллельного переноса фронта
сорбции приводит к известному уравнению Шилова, которое записывается
следующим образом:
пр kx 0
где τпр – время защитного действия слоя, k – коэффициент защитного
действия, τ0 – потеря времени защитного действия.
Основной особенностью подхода
Шилова
можно
считать
выделение на фронте адсорбции
некоторой точки, движущейся с
постоянной скоростью, которая
получила
название
«центр
тяжести» сорбционной волны.
24.
МОДЕЛИ ДИНАМИКИ АДСОРБЦИИМодели однокомпонентной неравновесной изотермической
адсорбции T=const
a c
a
2c
w
D 2
x
x
a
( а, с )
a f (c)
Предпоследняя строчка представляет собой уравнение кинетики в общей
форме.
В случае выпуклой изотермы адсорбции
существуют предпосылки, необходимые
для возникновения режима параллельного
переноса
фронта
сорбции
на
асимптотической стадии процесса.
Конечная скорость массообмена вызывает
растяжение фронта сорбции, выпуклая
изотерма способствует его сжатию.
25.
МОДЕЛИ ДИНАМИКИ АДСОРБЦИИМодели однокомпонентной неизотермической адсорбции
T≠const
a c
c
2c
w D* 2
x
x
H
T
T
a
whг
Q
0
x
а* f ( c ,Т )
где Н – суммарная теплоемкость, а' – равновесная величина адсорбции,
а* – предельная величина адсорбции, D* – коэффициент продольной
диффузии; Q – тепловой эффект сорбции; hг – теплоемкость газа.
Замечание: При протекании неизотермического процесса адсорбционная
и тепловая волны будут двигаться взаимосогласованно.
Случай 1. Когда скорость тепловой волны (U) больше скорости движения
изотермического фронта (Wизо), все выделяющееся при адсорбции тепло
отводится проходящим потоком, и адсорбция протекает при холодном
сорбенте.
В этом случае теплота адсорбции не оказывает влияния на процесс.
26.
МОДЕЛИ ДИНАМИКИ АДСОРБЦИИПо адсорбенту распространяются две волны (Рис. а):
1.
Тепловая со скоростью U при с=0
2.
Сорбционная со скоростью W при c=c0 и а=а0
Соотношение между адсорбционным и тепловым фронтами
Случай 2. Если скорость изотермической адсорбционной волны (Wизо)
больше, чем скорость тепловой, то выделяющееся при поглощении тепло
не успевает отводиться потоком.
Это приводит к снижению статической активности адсорбента в зоне
поглощения.
На нагретом участке поглощается не весь адсорбат, а лишь часть его.
Поэтому по адсорбенту распространяются две сорбционные волны (Рис. б)
27. Модели динамики адсорбции
МОДЕЛИ ДИНАМИКИ АДСОРБЦИИМодели многокомпонентной изотермической адсорбции T=const
Слой адсорбента ОА – полностью
насыщен смесью обоих веществ.
Он
содержит
а12
(индексы
рассматриваемых
компонентов)
первого компонента, находящегося в
равновесии
с
начальной
концентрацией его в газовой фазе
с01 и со вторым компонентом,
величина адсорбции которого а21
при равновесной концентрации с02.
Распределение 2-х адсорбатов по длине
слоя
адсорбента
для
некоторого
достаточно большого момента времени
Слой адсорбента АВ насыщен первым компонентом смеси, но
представляет собой работающий слой для второго компонента. В слое ВС
находится адсорбент, насыщенный только первым компонентом, а слой
CD является зоной поглощения первого компонента.
Так как величина адсорбции первого компонента понижается в
присутствии второго, то величина адсорбции его в области ВС выше, чем в
области ОА. Поэтому при перемещении работающего слоя АВ вдоль
длины слоя происходит частичное вытеснение первого компонента,
пропорциональное площади с двойной штриховкой.
28.
МОДЕЛИ ДИНАМИКИ АДСОРБЦИИПо этой причине концентрация первого компонента на участке ВС (с'1)
выше начальной концнтрации (с01):
с1 с1 с2
где α– коэффициент вытеснения.
Поступательное перемещение работающих слоев АВ и CD происходит со
скоростями:
W1 wc1 / a1
W2 wc02 / a 21
Анализ материальных балансов дает следующее
коэффициента вытеснения:
а1 а12 / а21
выражение
для
который теоретически зависит только от равновесных факторов –
величин адсорбции.
Поскольку W1>W2 расстояние между фронтами АВ и CD постепенно
увеличивается.
Представленная модель легко обобщается на случай сорбции смеси с
любым числом компонентов.
29. Модели динамики адсорбции
МОДЕЛИ ДИНАМИКИ АДСОРБЦИИМодели однокомпонентной неизотермической
адсорбции T≠const
T
T
a
a c
c
2c
H
whГ
Q
0
w
D 2
x
x
x ;
a f ( c, T )
Модели однокомпонентной неравновесной
изотермической адсорбции T=const
a c
a
2c
w
D 2
x
x
;
a
( а, с ) ;
a f (c)
Модели однокомпонентной равновесной
изотермической адсорбции T=const
a c
c
2c
w
D 2
x
x
;
a f (c)
Основные группы параметров моделей
Влагоемкость сорбента в статических
условиях
а’ – предельная величина адсорбции,
c’ - равновесная концентрация адсорбтива
Влагоемкость сорбента в динамических
условиях
a – адсорбционная способность,
c – концентрация адсорбтива,
τ –время,
w – скорость потока газа,
1/γ – коэффициент Генри,
φ – влажность газа,
D’ - коэффициент продольной диффузии
Термодинамические и кинетические
параметры сорбента
Н – суммарная теплоемкость адсорбента и
Упрощение моделей однокомпонентной равновесной адсорбата,
изотермической адсорбции
hГ – теплоемкость газа,
Q – теплота адсорбции,
a c
c
1
a
a c ;
w 0; a f (c)
c a
β –кинетический коэффициент.
x
t
В существующих методиках расчета в полном объеме не учитывается влияние случайных
составляющих сорбционных процессов.
29
30. Лекция 24. Вероятностно-статистическая модель процесса осушки воздуха силикагелем
ЛЕКЦИЯ 24. ВЕРОЯТНОСТНО-СТАТИСТИЧЕСКАЯ МОДЕЛЬПРОЦЕССА ОСУШКИ ВОЗДУХА СИЛИКАГЕЛЕМ
Динамика сорбционных фронтов
с
cw=c
c′s w≠cs
c0
0
t; T=const;
Адсорбционный фронт
D′
D′D
AD
Десорбционный фронт
L
A
S
Пусть
процесс
изотермической
адсорбционной
осушки
воздуха
силикагелем
происходит
в
цилиндрическом адсорбере с неподвижным
однородным
слоем
адсорбента
с
неизменными свойствами, длиной – L0 и
осредненной
площадью
свободного
поперечного сечения – F0. Введем в
рассмотрение систему отсчета, связанную с
координатой оси симметрии адсорбера – S
и временем – t, которое отсчитывается с
начала процесса подачи влажного воздуха
в адсорбер – t=t0=0.
Допуская, что на силикагеле сорбируется лишь один компонент – влага,
будем считать, что несущая среда – воздух, является несжимаемой, а
концентрация влаги в ней настолько мала, что изменением плотности
потока из-за убыли адсорбтива можно пренебречь. Предположим, что в
полностью отрегенерированный адсорбент подается влажный воздух с
постоянной концентрацией – cw, равной концентрации насыщенных
паров воды – cs, и объемным расходом – Q0=Q0(t), а движение потока
воздуха в слое адсорбента происходит со средней скоростью –
W0=Q0/F0=W0(t) в направлении уменьшения концентрации адсорбата.
31.
ВЕРОЯТНОСТНО-СТАТИСТИЧЕСКАЯ МОДЕЛЬ ПРОЦЕССА ОСУШКИВОЗДУХА СИЛИКАГЕЛЕМ
В рамках сделанных допущений, используя уравнение материального
баланса, можно получить феноменологическую систему уравнений
динамики равновесной изотермической адсорбции с учетом процесса
продольной диффузии адсорбтива в слое адсорбента в виде:
a c
c
2c
W0
D 2
S
S
t t
a ( c )
(1)
где с – текущая концентрация адсорбтива в потоке, а и а’ соответственно,
равновесные ей величины адсорбции и концентрации адсорбата.
Поскольку равновесные величины а и а’ однозначно связаны между собой
соотношением a a N (ρN – насыпная плотность адсорбента) используя
метод подстановки, первое уравнение системы (1) можно представить как:
c( S , t )
c( S , t )
2 c( S , t )
W
D*
t
S
S 2
где W W0 /(1 N
da
)
dc
и D* D /(1 N
da
)
dc
(2)
– скорость движения адсорбтива по
слою адсорбента и эквивалентный коэффициент продольной диффузии
соответственно.
32.
ВЕРОЯТНОСТНО-СТАТИСТИЧЕСКАЯ МОДЕЛЬ ПРОЦЕССА ОСУШКИВОЗДУХА СИЛИКАГЕЛЕМ
Рассмотрим движение произвольной i-ой точки фронта адсорбции при
W0=const, D*=0 и наличии конечного градиента концентраций в
адсорбере. Согласно уравнению (2), средняя скорость произвольной i-ой
точки фронта адсорбции зависит от постоянной величины ρN и конечной
величины (da/dc)i ≥ 0, определяемой изотермой адсорбции для каждой
конкретной точки, и удовлетворяет закону Викке в виде:
da
(3)
Wi W0 /(1 N ( ) i )
dc
Выражение (3) позволяет констатировать, что в общем случае, любая i-ая
точка фронта адсорбции будет двигаться по слою адсорбента со своей
характерной скоростью – Wi
В случае выпуклой изотермы адсорбции, при условии, что ca < cb и
(da/dc)a > (da/dc)b, две произвольные точки (а) и (b) фронта адсорбции
будут непрерывно сближаться, стремясь образовать так называемый
«обрывный» фронт, т.к. согласно закону (3) Wa Wb . При этом «обрывный»
фронт должен распространяться со скоростью – WW , также определяемой
изотермой адсорбции, но удовлетворяющей закону Вильсона в виде:
WW W0 /(1 N aW / cW )
(4)
где концентрации адсорбтива в потоке cw, соответствует равновесная ей
величина адсорбции aw
Если, имеет место ca cW cb , то выполняется двойное неравенство Wa WW Wb
33.
ВЕРОЯТНОСТНО-СТАТИСТИЧЕСКАЯ МОДЕЛЬ ПРОЦЕССА ОСУШКИВОЗДУХА СИЛИКАГЕЛЕМ
В случае вогнутой изотермы адсорбции, согласно закону (3), для ca < cb
имеем: (da/dc)a < (da/dc)b и Wa Wb . Соответственно, точки (а) и (b)
постоянно удаляясь, друг от друга, обуславливают тенденцию к
неограниченному «размыванию» фронта адсорбции.
Можно выделить частный случай движения различных точек фронта
адсорбции Wa WW Wb
соответствующий согласно (3) и (4), либо линейной
изотерме адсорбции, либо условию распространения «обрывного» фронта.
Причем стационарный фронт адсорбции, при D*=0, сохраняя свою
первоначальную конфигурацию, будет перемещаться в режиме
параллельного переноса.
Независимо от вида изотермы и величины градиента концентраций,
присутствие диффузионных составляющих процесса (D*≠0) будет
способствовать
«размыванию»
фронта адсорбции
и
нарушению
«поршневой» структуры потока в зернистом слое.
Внимание! В общем случае (1) образует систему c нелинейным
дифференциальным уравнением в частных производных, аналитического
решения которой в настоящее время не получено.
34.
ВЕРОЯТНОСТНО-СТАТИСТИЧЕСКАЯ МОДЕЛЬ ПРОЦЕССА ОСУШКИВОЗДУХА СИЛИКАГЕЛЕМ
Замечание: Поскольку при рассмотрении большинства практических
вопросов динамики адсорбции, обычно не ставится задача точного
молекулярно-кинетического или микроскопического описания явлений,
при отыскании функций распределения адсорбтива и/или адсорбата в слое
адсорбента, наряду с феноменологическим подходом, может быть
также
использован
вероятностно-статистический
подход,
базирующийся на методах статистической физики.
При этом феноменологический подход может быть использован для
установления
функциональных
зависимостей
между
детерминированными
макроскопическими
величинами,
характеризующими протекание адсорбционных процессов.
Определяя стохастические составляющие адсорбционного процесса, будем
полагать, что в рабочей части адсорбера имеет место квазиустановившееся
стохастическое движение молекул воды, которое соответствует теории
случайных марковских процессов. Не снижая общности рассуждений, будем
считать
кинетическую
стадию
эволюции
рассматриваемой
системы
закончившейся на входе рабочего слоя адсорбента.
В результате чего, будем полагать, что в рабочей части адсорбера установилось
стационарное (равновесное) распределение потоков и происходит относительно
медленное изменение во времени концентрационных (гидродинамических)
параметров рассматриваемой макросистемы.
35.
ВЕРОЯТНОСТНО-СТАТИСТИЧЕСКАЯ МОДЕЛЬ ПРОЦЕССА ОСУШКИВОЗДУХА СИЛИКАГЕЛЕМ
Учитывая, быстрое завершение кинетической стадии эволюции системы
будем считать, что средние скорости несущей среды и адсорбтива
существенно отличаются друг от друга за счет протекания адсорбционных
процессов. Указанное обстоятельство позволяет ввести в рассмотрение
величину скорости движения фронта адсорбции по слою адсорбента – W.
Тогда, с учетом сделанных допущений, наряду со средней скоростью
движения фронта адсорбции
по
слою адсорбента
W’(S,t) в
рассматриваемом процессе будут постоянно присутствовать и случайные
~ , влиянием которых пренебречь нельзя,
составляющие этой скорости – W
что позволяет записать:
~
W W ( S , t ) W
(5)
~
Поскольку величина W
в выражении (5) обусловлена наличием случайных
составляющих, действующих на молекулы адсорбтива и/или адсорбата,
как со стороны потока несущей среды, так и адсорбента, то и скорость W, и
координата S, также будут случайными величинами.
В результате, становится очевидным, что распределение молекул
адсорбтива и/или адсорбата на фронте адсорбции в осевом направлении в
любой момент времени можно охарактеризовать статистически с помощью
функции плотности распределения f=f(S, t), нормированной на единицу.
36.
ВЕРОЯТНОСТНО-СТАТИСТИЧЕСКАЯ МОДЕЛЬ ПРОЦЕССА ОСУШКИВОЗДУХА СИЛИКАГЕЛЕМ
По определению величина f(S,t)dS представляет собой вероятность того,
что произвольно выбранная молекула адсорбтива и/или адсорбата будет
иметь, в момент времени t, координату в интервале (S, S+dS).
Будем считать, что случайные составляющие скорости δ-коррелированы во
времени и их свойства удовлетворяют допущениям теории случайных
марковских процессов. Тогда, для описания гидродинамической стадии
эволюции системы в пространстве S мы можем воспользоваться известным
кинетическим уравнением ФПК в виде:
f ( S , t )
1 2
(W ( S , t ) f ( S , t ))
( B0 ( S , t ) f (S , t ))
2
t
S
2 S
(6)
где W’(S,t) и B0(S,t) – величины, характеризующие в пространстве S
соответственно среднюю детерминированную скорость эволюции системы и
интенсивность случайных составляющих протекающих процессов.
Имея наглядную интерпретацию, аналогичную по виду обычному
уравнению неразрывности, уравнение (6) позволяет обобщить многие
феноменологические зависимости, в том числе, полученные из уравнений
материального баланса.
37.
ВЕРОЯТНОСТНО-СТАТИСТИЧЕСКАЯ МОДЕЛЬ ПРОЦЕССА ОСУШКИВОЗДУХА СИЛИКАГЕЛЕМ
Используя обобщенный принцип суперпозиций можно показать, что если
некоторая функция f(S,t,α) по переменным (S,t) удовлетворяет линейному
дифференциальному уравнению L(f)=0 при любом фиксированном
значении параметра α, то интеграл c( S , t ) f ( S , t , ) ( )d также является
решением того же уравнения L(f)=0, если производные, входящие в
линейный дифференциальный оператор L(f), можно вычислить при
помощи дифференцирования под знаком интеграла.
Таким образом, в рассматриваемых условиях, величины W’(S,t) и B0(S,t),
входящие в уравнение (6) могут быть определены через соответствующие
величины W’ и D* уравнения (2), в виде:
W ( S , t ) W (t ) W0 (t ) /(1 N
da
)
dc
B0 ( S , t ) 2 D* 2 D /(1 N
da
)
dc
Анализ величин W’(S,t) и B0(S,t), входящих в уравнение (6), показывает,
что в рамках сделанных допущений будем исходно предполагать
независимость средней скорости движения фронта адсорбции от
координаты W’(S,t)= W’(t) и стационарность интенсивности случайных
возмущений процесса B0= B0(S)=const.
38.
ВЕРОЯТНОСТНО-СТАТИСТИЧЕСКАЯ МОДЕЛЬ ПРОЦЕССА ОСУШКИВОЗДУХА СИЛИКАГЕЛЕМ
Тогда, для описания гидродинамической стадии эволюции системы в
пространстве S уравнение (6) можно представить в виде:
B0 2
f ( S , t )
W (t )
f (S , t )
f (S , t )
2
t
S
2 S
(7)
Решения уравнения (7) уже могут быть представлены в виде
элементарных функций, что в свою очередь значительно расширяет
возможности практического применения уравнения ФПК.
Замечание: Применительно ко многим адсорбционным процессам,
уравнение ФПК выполняет важную роль связующего звена между теорией
дифференциальных уравнений и теорией случайных процессов.
В результате, применительно к нахождению функции распределения
адсорбтива и/или адсорбата в слое адсорбента для рассматриваемых
условий появляется возможность установить взаимосвязь между
результатами
исследований
вероятностно-статистического
и
феноменологического подходов.
39. Лекция 25. Вероятностно-статистическая модель процесса осушки воздуха силикагелем
ЛЕКЦИЯ 25. ВЕРОЯТНОСТНО-СТАТИСТИЧЕСКАЯ МОДЕЛЬПРОЦЕССА ОСУШКИ ВОЗДУХА СИЛИКАГЕЛЕМ
Изотермы адсорбции паров воды на силикагеле состоят из 3-х различных
определяющих участков.
Вид изотермы адсорбции паров воды на силикагеле
По мере возрастания относительного влагосодержания среды φ=c/cs,
первый участок с выпуклой изотермой адсорбции, выходящий
практически из нуля, пройдя первую точку перегиба (B) изотермы при
φ=0,2-0,3, плавно переходит во второй участок с вогнутой изотермой
адсорбции. Этот участок заканчивается во второй точке перегиба
изотермы при φ=0,5-0,6 и переходит в третий участок с выпуклой
изотермой адсорбции, на котором при φ>0,9 величина da/dc→0.
40.
ВЕРОЯТНОСТНО-СТАТИСТИЧЕСКАЯ МОДЕЛЬ ПРОЦЕССА ОСУШКИВОЗДУХА СИЛИКАГЕЛЕМ
Таким образом, при адсорбции паров воды на силикагеле,
параллельный перенос стационарного участка фронта адсорбции в
слое адсорбента может происходить лишь на первом и третьем участке
изотермы адсорбции.
Только здесь могут одновременно возникнуть условия, как для
формирования «обрывного» фронта (выпуклая изотерма адсорбции), так и
проявления эффекта «размывания» фронта адсорбции под действием
случайных составляющих процесса.
Внимание! При наличии двух противоположно действующих эффектов
по истечению некоторого времени их действие взаимно компенсируется и
стационарный участок фронта адсорбции начнет перемещаться по слою
адсорбента в режиме параллельного переноса.
В результате при W0(S)=const на первом участке изотермы при φ≤0,2-0,3
среднюю скорость движения стационарного фронта можно вычислить по
формуле:
c
WI W0 I
(8)
N aI
где cI и aI – величины концентрации адсорбтива и адсорбции в первой
точке перегиба (B).
41.
ВЕРОЯТНОСТНО-СТАТИСТИЧЕСКАЯ МОДЕЛЬ ПРОЦЕССА ОСУШКИВОЗДУХА СИЛИКАГЕЛЕМ
Зависимость (8) получена из уравнения линейной изотермы адсорбции
(изотерма Генри) при условии, что cI << ρNaI , т.к. в этом случае
WI W0 /(1 N
da I
c
) W0 c I /(c I N a I ) W0 I
dc I
N aI
Величина ρNaI/cI=ρNdaI/dcI=kA будет
характеризовать
тангенс
угла
наклона
касательной
некоторой
точки (А) первого участка изотермы
c
адсорбции, а величина WI W0 I WA
N aI
– среднюю скорость движения
некоторой точки фронта адсорбции с
концентрацией cA.
Соответственно, при W0(S)=const и B0 = 0, исходя из закона (3), все точки
(а) фронта адсорбции с концентрацией ca, меньшей чем в точке (А), будут
двигаться медленнее, чем точка с концентрацией cA, а все точки (b)
фронта с большей концентрацией cb – быстрее, стремясь образовать
«обрывный» фронт адсорбции, движущийся со скоростью:
W A W0 c I /(c I N a I ) W0
cI
N aI
42.
ВЕРОЯТНОСТНО-СТАТИСТИЧЕСКАЯ МОДЕЛЬ ПРОЦЕССА ОСУШКИВОЗДУХА СИЛИКАГЕЛЕМ
Осуществляя параллельный перенос
касательной точки (А), можно
получить
точки
(C)
и
(D),
принадлежащие
соответственно
второму
и
третьему
участкам
изотермы адсорбции. При B0 = 0,
точки
фронта
адсорбции
с
концентрациями cA, cС и cD,
согласно
закону
(3),
должны
двигаться в режиме параллельного
переноса с одинаковыми средними
скоростями движения WI WA WC WD
В результате, любая i-ая точка фронта адсорбции, удовлетворяющая
условию ci (c A ; cC )будет стремиться к точке фронта с концентрацией cA, а
любая i-ая точка фронта адсорбции удовлетворяющая условию ci (cC ; c D ) – к
точке с концентрацией cD, способствуя неограниченному «размыванию»
фронта адсорбции между точками с концентрациями cA и cD.
Другая точка перегиба изотермы адсорбции с величинами концентрации
адсорбтива и адсорбции – cIII и aIII, на фронте адсорбции будет иметь
минимальную среднюю скорость движения WIII W0 /(1 N
da III
)
dc III
43.
ВЕРОЯТНОСТНО-СТАТИСТИЧЕСКАЯ МОДЕЛЬ ПРОЦЕССА ОСУШКИВОЗДУХА СИЛИКАГЕЛЕМ
Подобное поведение точек фронта адсорбции, при W0= W0(t) и tI>tII, в
первом приближении можно смоделировать путем рассмотрения в
пространстве и времени двух независимых множеств адсорбтива,
имеющих функции плотности распределения fI(S,tI) и fII(S,tII),
нормированные на единицу и соответствующие выпуклым участкам
изотермы адсорбции, которые перемещаются по слою адсорбента с
различными средними скоростями:
c
WI (t I ) W A (t I ) W0 (t I ) c I /(c I N a I ) W0 (t I ) I
(9)
N aI
WII (t II ) W0 (t II ) /(1 N
aD aC
cD cC
) W0 (t II )
cD cC
N (aD aC )
(10)
Зависимость (10) получена из
уравнения
линейной
изотермы
адсорбции, проходящей через точки
(C) и (D), которые соответственно
принадлежат второму и третьему
участкам изотермы адсорбции, при
условии, что (c D cC ) N (a D aC )
44.
ВЕРОЯТНОСТНО-СТАТИСТИЧЕСКАЯ МОДЕЛЬ ПРОЦЕССА ОСУШКИВОЗДУХА СИЛИКАГЕЛЕМ
Осуществляя параллельный перенос
линейной
изотермы
адсорбции,
проходящей через точки (C) и (D),
можно получить точки (C′) и (D′),
принадлежащие
соответственно
второму
и
третьему
участкам
изотермы адсорбции. При B0 = 0,
точки
фронта
адсорбции
с
концентрациями cС′ и cD′, согласно
закону (3), также должны двигаться
в режиме параллельного переноса с
одинаковыми средними скоростями
движения WII (t II ) WC (t II ) WD (t II )
В результате, любая i-ая точка фронта адсорбции, удовлетворяющая
условию ci (cC ; c D ) , будет стремиться к точке фронта адсорбции с
концентрацией cD′, способствуя как «размыванию» участка этого фронта
между точками с концентрациями cС′ и cIII, так одновременному
формированию «обрывного» участка фронта для второго множества
адсорбтива с функцией плотности распределения fII(S,tII).
45.
ВЕРОЯТНОСТНО-СТАТИСТИЧЕСКАЯ МОДЕЛЬ ПРОЦЕССА ОСУШКИВОЗДУХА СИЛИКАГЕЛЕМ
Поскольку для любых t>0 справедливо
W
, II (tII ) WI (tI ) определяющая точка с
концентрацией cD′ фронта адсорбции
второго множества адсорбтива будет
непрерывно
отставать
от
определяющей точки с концентрацией
cA
фронта
адсорбции
первого
множества адсорбтива, тем самым,
моделируя
«размывание»
фронта
адсорбции, обусловленное вогнутым
участком изотермы адсорбции.
Точки фронтов адсорбции с концентрациями cA и cD′ можно рассматривать
в качестве определяющих в виде неких «центров» этих фронтов,
движущихся со средними скоростями WII (t II ) и WI, (t I )удовлетворяющими
выражениям (9) и (10).
46.
ВЕРОЯТНОСТНО-СТАТИСТИЧЕСКАЯ МОДЕЛЬ ПРОЦЕССА ОСУШКИВОЗДУХА СИЛИКАГЕЛЕМ
Для различных коэффициентов продольной диффузии DI и DII,
рассматриваемых множеств адсорбтива, из уравнения (7), с учетом (9) и
(10) получаем:
где
f I ( S , tI )
BI 2
WI ( tI )
f I ( S , tI )
f I ( S , tI )
tI
S
2 S 2
(11)
f II ( S , t II )
BII 2
WII (t II )
f II ( S , t II )
f II ( S , t II )
t II
S
2 S 2
(12)
BI 2 DI cI /( cI N aI ) 2 DI
cI
N aI
и
BII 2 DII /(1 N
aD aC
cD cC
) 2 DII
cD cC
N (aD aC )
С помощью уравнений (11) и (12) можно описать поведение всего фронта
адсорбции в целом. Однако они, используя линейные изотермы адсорбции,
не учитывают условий формирования «обрывного» фронта, характерных
для выпуклых участков изотермы адсорбции.
47.
ЛЕКЦИЯ 26. ВЕРОЯТНОСТНО-СТАТИСТИЧЕСКАЯ МОДЕЛЬПРОЦЕССА ОСУШКИ ВОЗДУХА СИЛИКАГЕЛЕМ
Переходя в подвижные системы координат, связанные с определяющими
tI
t II
0
0
точками фронтов адсорбции, путем замены x I S WI (t I )dt I и x II S WII (t II )dt II
bI=BI/2, bII=BII/2 из (11) и (12) соответственно находим:
f II
2 f II
bII
2
t II
x II
f I
2 fI
bI
2
t I
x I
После ввода в два последних уравнения дополнительных членов,
существование которых не следует из уравнения материального баланса,
которые учитывают влияние нелинейности выпуклых участков изотермы
адсорбции, имеем:
f I
( x I f I )
2 fI
kI
bI
(13)
2
t I
x I
x I
f II
( x II f II )
2 f II
k II
bII
2
t II
x II
x II
где kI и kII – некоторые постоянные коэффициенты.
(14)
48.
ВЕРОЯТНОСТНО-СТАТИСТИЧЕСКАЯ МОДЕЛЬ ПРОЦЕССА ОСУШКИВОЗДУХА СИЛИКАГЕЛЕМ
Исходные замены f I ( x I , t I ) exp( k I t I )u I ( x I , t I )
и
f II ( xII , t II ) exp( k II t II )u II ( xII , t II )
в уравнениях (13) и (14) приводят к уравнениям вида:
u I
u I
2u I
k I xI
bI
2
t I
x I
x I
u II
u II
2 u II
k II x II
bII
2
t II
x II
x II
(15)
(16)
а последующий переход от tI, xI и tII, xII, к I exp( 2k I t I ) /( 2k I ) , z I xI exp( k I t I )
и II exp( 2k II t II ) /( 2k II ), z II xII exp( k II t II ) соответственно приводит к уравнениям:
u I
2u I
bI
2
I
z I
u II
2 u II
bII
2
II
z II
Внимание! Данные уравнения аналогичным уравнениям тепло- и
массопереноса, точные решения которых хорошо известны.
49.
ВЕРОЯТНОСТНО-СТАТИСТИЧЕСКАЯ МОДЕЛЬ ПРОЦЕССА ОСУШКИВОЗДУХА СИЛИКАГЕЛЕМ
Для задачи Коши, при –∞ < zI < ∞ и –∞ < zII < ∞ , находим:
u I ( z I , I )
u II ( z II , II )
(zI I )2
exp(
) 0, I ( I )d I
4
b
bI I
I I
CI
C II
bII II
( z II II ) 2
exp(
) 0, II ( II )d II
4bII II
где CI и CII – некоторые постоянные. Переход к переменным tI, xI и tII, xII
дает:
2 bI
u I (xI , t I ) CI
(exp( 2k I t I 1)
kI
2 bII
u II ( x II , t II ) C II
(exp( 2k II t II 1)
k II
1 / 2
k I ( x I exp( k I t I ) I ) 2
exp 2bI (exp( 2k I t I ) 1) 0, I ( I )d I
1 / 2
k II ( x II exp( k II t II ) II ) 2
exp 2bII (exp( 2k II t II ) 1) 0,II ( II )d II
50.
ВЕРОЯТНОСТНО-СТАТИСТИЧЕСКАЯ МОДЕЛЬ ПРОЦЕССА ОСУШКИВОЗДУХА СИЛИКАГЕЛЕМ
Возвращаясь к функциям fI(xI,tI) и fII(xII,tII), для начальных условий
f0,I=f0(xI,0) при tI=0 и f0,II=f0(xII,0) при tII=0 имеем:
f I (xI , t I ) CI e
f II ( x II , t II ) C II e
2 bI 2 k I t I
(
e
1
)
kI
1 / 2
2 bII 2 k II t II
(
e
1
)
k
II
1 / 2
kI tI
k II t II
k I ( x I e kI tI I ) 2
exp 2bI (e 2kI tI 1) f 0,I ( I )d I
k II ( x II e k II t II II ) 2
exp 2bII (e 2kII tII 1) f 0, II ( II )d II
Тогда, для функций распределения fI(S,tI) и fII(S,tII), можно записать:
B
f I ( S , t I ) C I e k I tI I (e 2 k I tI
kI
B
f II ( S , t II ) C II e k II t II II ( e 2 k II t II
k II
tI
k I tI
2
1 / 2
k I (( S WI (t I )dt I )e I )
0
f ( )d
1)
exp
I
2 k I tI
0, I I
BI (e
1)
t II
k II t II
2
k
((
S
W
(
t
)
dt
)
e
)
1 / 2
II
II
0 II II II
f ( )d
1)
exp
II
2 k II t II
0, II II
B II ( e
1)
(17)
(18)
51.
ВЕРОЯТНОСТНО-СТАТИСТИЧЕСКАЯ МОДЕЛЬ ПРОЦЕССА ОСУШКИВОЗДУХА СИЛИКАГЕЛЕМ
Окончательно, для функции плотности распределения f = f(S, t) получаем:
f f (S , t ) f I (S , t I ) f II (S , t II )
B
C I e k I t I I (e 2 k I t I
kI
tI
kI tI
2
k
((
S
W
(
t
)
dt
)
e
)
1 / 2
I
I I
I
I
0
f ( )d
1)
exp
I
2
k
t
I
I
0, I I
BI (e
1)
B
C II e k II tII II ( e 2 k II tII
k II
t II
k II t II
2
k
((
S
W
(
t
)
dt
)
e
)
1 / 2
II
II
0 II II II
f ( )d
1) exp
II
2 k II t II
0, II II
BII ( e
1)
(19)
Формула (19), определяет явный вид искомой функции f = f(S, t) и
позволяет решить целый ряд важных практических задач. Используя ее,
можно найти распределение концентрации адсорбтива и/или адсорбата по
длине слоя адсорбента в любой момент времени, в зависимости от
конструктивных и технологических параметров процесса, таких как L0, Q0,
F0, D, a (c) , ρN и т.д.
Кроме того, появляется возможность рассчитать динамическую активность
слоя адсорбента, время защитного действия адсорбера, длину фронта
адсорбции и целый ряд других величин.
52.
ВЕРОЯТНОСТНО-СТАТИСТИЧЕСКАЯ МОДЕЛЬ ПРОЦЕССА ОСУШКИВОЗДУХА СИЛИКАГЕЛЕМ
Применительно к процессам с безнагревной регенерацией адсорбента –
путем снижения давления и продувки адсорбента противотоком частью
осушенного потока, выражение (19), при tI=tKI и tII=tKII, где tKI и tKII –
длительности процессов адсорбции соответствующих множеств, может
рассматриваться в качестве начального распределения процесса
десорбции:
fНD = fНD(SНD, tК) = fНDI(SНDI, tКI) +fНDII(SНDII, tКII)
Пусть, при регенерации, в слой адсорбента, начиная с моментов времени
tDI = t – tKI и tDI = t – tKII , подается осушенный воздух с концентрацией –
cW c D и объемным расходом – QD QD (t D ) , а движение потока воздуха в
слое адсорбента происходит со средней скоростью – WD QD / F0 WD (t D )
в направлении увеличения концентрации адсорбата.
Тогда,
WDI (t DI ) WD (t DI ) c I /(c I N a I ) WD (t DI )
(tDII ) WD (tDII ) /(1 N
WDII
a DD aC D
c DD cC D
) WD (tDII )
c I
N a I
c DD cC D
N (a D aC )
D
D
53.
ВЕРОЯТНОСТНО-СТАТИСТИЧЕСКАЯ МОДЕЛЬ ПРОЦЕССА ОСУШКИВОЗДУХА СИЛИКАГЕЛЕМ
С учетом сказанного, уравнения (11) и (12) принимают вид:
f DI ( S , t DI )
BDI 2
WDI (t DI )
f DI ( S , t DI )
f DI ( S , t DI )
t DI
S
2 S 2
(20)
f DII ( S , t DII )
BDII 2
(t DII )
WDII
f DII ( S , t DII )
f II ( S , t DII )
2
t DII
S
2 S
(21)
(t DII ) 0, а
Здесь: WDI (t DI ) 0 и WDII
B DI 2 DDI c I /(c I N a I ) 2 DDI
BDII 2 DDII /(1 N
c I
N a I
a DD aC D
c DD cC D
) 2 DDII
c DD cC D
N (a DD aC D )
Переход в подвижные системы координат, связанные с определяющими
tDI
t DII
0
0
точками фронтов десорбции, путем замены xDI S WDI (t DI )dt DI и xDII S WDII
(t DII )dt DII
bDI=BDI/2, bDII=BDII/2 из (20) и (21) позволяет получить:
f DI
2 f DI
bDI
2
t DI
x DI
(22)
f DII
2 f DII
bDII
2
t DII
x DII
(23)
54.
ВЕРОЯТНОСТНО-СТАТИСТИЧЕСКАЯ МОДЕЛЬ ПРОЦЕССА ОСУШКИВОЗДУХА СИЛИКАГЕЛЕМ
В отличие от адсорбционных процессов, введение в рассмотрение
дополнительных членов в уравнениях (22) и (23) здесь не требуется, т.к.
влияние нелинейности выпуклых участков изотермы адсорбции в
десорбционных процессах способствует «размыванию» фронта адсорбции и
может быть учтено с помощью величин bDI и bDII.
Для задачи Коши, при –∞ < xDI < ∞ и –∞ < xDII < ∞ , с начальными
условиями f0,DI=f0(xDI,0) при tDI=0 и f0,DII=f0(xDII,0) при tDII=0 находим:
f DI ( x DI , t DI )
2
f DII ( x DII , t DII )
2
C DI
bDI t DI
C DII
bDII t DII
( x DI DI ) 2
exp(
) 0, DI ( DI )d DI
4bDI t DI
(24)
( x DII DII ) 2
exp(
) 0, DII ( DII )d DII
4bDII t DII
(25)
где CDI и CDII – постоянные, определяемые из условий нормировки.
55.
ВЕРОЯТНОСТНО-СТАТИСТИЧЕСКАЯ МОДЕЛЬ ПРОЦЕССА ОСУШКИВОЗДУХА СИЛИКАГЕЛЕМ
Возвращаясь к исходным переменным получаем:
f D (S , t ) f DI (SDI , tDI ) f DII (SDII , tDII )
C DI
2 BDI t DI
C DII
2 BDII t DII
t DI
2
(t DI )dt DI ) DI )
(( S WDI
0
f ( )d
DI
exp
0, DI DI
2 BDI t DI
t DII
2
(t DII )dt DII ) DII )
(( S WDII
0
f
0, DII ( DII ) d IDI
exp
2 BDII t DII
Основываясь на явном выражении для функции fD = fD(S, t) можно:
Рассчитать время протекающего процесса;
Оценить степень регенерации сорбента;
Найти положение сорбционных фронтов и т.д.
(26)
56.
ВЕРОЯТНОСТНО-СТАТИСТИЧЕСКАЯ МОДЕЛЬ ПРОЦЕССА ОСУШКИВОЗДУХА СИЛИКАГЕЛЕМ
Рассмотренная модель может быть также использована и для расчета
процесса осушки газов с небольшим содержанием влаги, которые имеют
температуру точку росы ниже минус 40оС. Для этого необходимо ввести в
рассмотрение дополнительный («нулевой»), практически линейный,
участок изотерм адсорбции соответствующий небольшому содержанию
влаги.
Тогда, в рамках сделанных допущений и обозначений, с учетом (8) и (11),
среднюю скорость движения стационарного фронта W0 и интенсивность
случайных составляющих протекающих процессов B0 на «нулевом» участке
можно рассчитать по формулам:
W0 W0
c0
k0
N a0
B0 2D0 c0 /(c0 N a0 ) 2D0
c0
N a0
при этом W0 WI и W0 WII .
По аналогии с выражением (11)
f 0 ( S , t 0 )
B0 2
W0 (t 0 )
f 0 (S , t 0 )
f 0 (S , t 0 )
2
t 0
S
2 S
57.
ВЕРОЯТНОСТНО-СТАТИСТИЧЕСКАЯ МОДЕЛЬ ПРОЦЕССА ОСУШКИВОЗДУХА СИЛИКАГЕЛЕМ
t0
После перехода в подвижную систему координат, путем замены x0 S W0 (t0 )dt0
2
0
при b0 B0 / 2 , имеем: f 0 b f 0
t 0
0
x 0
2
( x0 0 ) 2
Для задачи Коши, при –∞ < x0 < ∞ находим: f 0 ( x0 , t 0 )
exp(
) 0,0 ( 0 )d 0
4
b
t
0 0
2 b0 t 0
C0
Возвращаясь к исходным переменным, для адсорбционного процесса
окончательно получаем:
t0
2
((
S
W
(
t
)
dt
)
)
0 0
0
0
C0
0
f ( )d
f f ( S , t ) f 0 ( S , t0 ) f I ( S , t I ) f II ( S , t II )
exp
0
0, 0 0
2 B0 t0
2 B0 t0
tI
kI tI
2
k
((
S
W
(
t
)
dt
)
e
)
1 / 2
I
I
I
I
I
k I t I B I
2kI tI
0
f ( )d
CI e
(e
1)
exp
I
2kI tI
0, I I
B I (e
1)
kI
B
C II e k II tII II ( e 2 k II tII
k II
t II
k II t II
2
k
((
S
W
(
t
)
dt
)
e
)
1 / 2
II
II
0 II II II
f ( )d
1)
exp
II
2 k II t II
0, II II
BII ( e
1)
(27)
58.
ВЕРОЯТНОСТНО-СТАТИСТИЧЕСКАЯ МОДЕЛЬ ПРОЦЕССА ОСУШКИВОЗДУХА СИЛИКАГЕЛЕМ
В этом случае, для десорбционного процесса, аналогично выводу формул
(20)-(27) имеем:
f D (S , t ) f D0 (S D0 , t D0 ) f DI (S DI , t DI ) f DII (S DII , t DII )
CD 0
2 BD 0t D 0
tD 0
2
(( S WD 0 (t D 0 )dt D 0 ) D 0 )
0
f ( )d
D0
exp
0, D 0 D 0
2 BD 0t D 0
C DI
2 BDI t DI
C DII
2 BDII t DII
t DI
2
(( S WDI (t DI )dt DI ) DI )
0
f ( )d
DI
exp
0, DI DI
2 BDI t DI
t DII
2
((
S
W
(
t
)
dt
)
)
DII DII
DII
DII
0
f
( )d IDI
exp
0, DII DII
2 BDII t DII
(28)
59.
Учет фактических характеристик изотермы адсорбции паров воды на силикагелеВведение дополнительных членов в
адсорбционный процесс, учитывающих
влияние нелинейности выпуклых участков
изотермы адсорбции с помощью
коэффициентов – kI, kII
Переход в подвижную систему
координат, связанную с
определяющими точками независимых
фронтов адсорбции
Адсорбция
Адсорбция
f I
( xI fI )
2 fI
kI
bI
2
t I
x I
x I
x I S WI ( t I )dt I
f II
( x II f II )
2 f II
k II
bII
2
t II
x II
x II
bI BI / 2
bII BII / 2
Десорбция
Десорбция
f DI
2 f DI
bDI
2
t DI
x DI
f DII
2 f DII
bDII
2
t DII
x DII
x II S WII ( t II )dt II
( t DII )dt DII
x DI S WDI ( t DI )dt DI x DII S WDII
bDI BDI / 2
bDII BDII / 2
Адсорбция
f f I ( S , t I , W I , f 0 , I , C I , BI , k I ) f II ( S , t II , W II , f 0 , II , C II , BII , k II )
Десорбция
, f 0 , DI , C DI , BDI ) f DII ( S , t DII , W DII
, f 0 , DII , C DII , BDII )
f D f DI ( S , t DI , W DI
60.
ЛЕКЦИЯ 27. ИССЛЕДОВАНИЕ АСИМПТОТИЧЕСКИХ СВОЙСТВМОДЕЛИ ПРОЦЕССА ОСУШКИ ВОЗДУХА СИЛИКАГЕЛЕМ
С целью выявления особенностей протекающих процессов и упрощения вида
полученных функций плотности распределения f(S, t) и fD(S,t) будем считать,
что каждое из рассматриваемых двух независимых множеств адсорбтива,
соответствующих выпуклым участкам изотермы адсорбции паров воды на
мелкопористом силикагеле, исходно подается на вход адсорбера в виде
ступенчатого возмущения.
Это позволяет представить функции начальных распределений f0,I=f0,I(S,0) и
f0,II=f0,II(S,0) в виде δ-функций Дирака f0,I=f0,I(S)=δ(ξI) и f0,II=f0,II(S)=δ(ξII).
Тогда, согласно определению δ-функций, имеем:
f ( ) ( )d f (0)
где f(ξ) – произвольная функция, непрерывная в точке ξ=0, что позволяет
записать выражение (19) в виде:
tI
kI tI 2
k
((
S
W
(
t
)
dt
)
e
)
1 / 2
I
I I
I
k I t I BI
2kI tI
0
f f ( S , t I , t II ) f I ( S , ti ) f II ( S , t II ) C I e
(e
1) exp
2
k
t
I
I
BI (e
1)
kI
B
C II e k II tII II ( e 2 k II tII
k II
t II
k II t II 2
k
((
S
W
(
t
)
dt
)
e
)
1 / 2
II
0 II II II
1) exp
2 k II t II
BII ( e
1)
(29)
61.
ИССЛЕДОВАНИЕ АСИМПТОТИЧЕСКИХ СВОЙСТВ МОДЕЛИ ПРОЦЕССАОСУШКИ ВОЗДУХА СИЛИКАГЕЛЕМ
Очевидно, что при exp( 2k I t I ) 1 и exp( 2k II t II ) 1,
с точностью необходимой для инженерных расчетов, можно считать
(exp( 2k I t I ) 1) exp( 2k I t I )
и
(exp( 2k II t II ) 1) exp( 2k II t II )
В результате выражение (29) принимает вид:
f f (S , t I , t II ) f I (S , t i ) f II (S , t II )
tI
t II
2
2
1 / 2
k I (( S WI (t I )dt I ))
1 / 2
k II (( S WII (t II )dt II ))
B I
B
0
0
II
C
CI
exp
II
exp
BI
k II
B II
kI
(30)
Замечание: Это соответствует режиму параллельного переноса
различных участков стационарных фронтов адсорбции двух независимых
множеств адсорбтива в слое адсорбента.
62.
ИССЛЕДОВАНИЕ АСИМПТОТИЧЕСКИХ СВОЙСТВ МОДЕЛИ ПРОЦЕССАОСУШКИ ВОЗДУХА СИЛИКАГЕЛЕМ
Действительно, переход к функциям fI(xI,tI) и fII(xII,tII) путем замены
tI
x I S WI (t I )dt I
t II
и x II S WII (t II )dt II в выражении (29), с учетом того, что
0
0
bI BI / 2 и bII BII / 2 , при 2k I t I 3 и 2k II t II 3 , дает:
f ( x1 , x II ) f , I x I f , II x II f x I , x II
2 bI
CI
kI
1 / 2
k I xI 2
2 bII
exp
C II
k II
2bI
Согласно выражению (31), при t I
3
2k I
и
1 / 2
t II
k II x II 2
exp
2
b
II
3
2k II
(31)
вид функций
распределения fI(xI,tI) и fII(xII,tII) не зависит от времени и практически не
отличается от предельных стационарных распределений f∞,I(xI) и f∞,II(xII),
f I ( x I , t I ) f , I ( x I ) и f II ( x II , t II ) lim f II ( x II , t II ) f , II ( x II )
т.е. имеет место: f I ( x I , t I ) tlim
t
I
II
Замечание: выражения (31) можно признать обоснованным только для
частного случая начальных условий, которые соответствуют допущениям о
ступенчатом вводе адсорбтива и полной исходной регенерации адсорбента.
63.
ИССЛЕДОВАНИЕ АСИМПТОТИЧЕСКИХ СВОЙСТВ МОДЕЛИ ПРОЦЕССАОСУШКИ ВОЗДУХА СИЛИКАГЕЛЕМ
Возвращаясь к рассмотрению уравнений (13) и (14), которые допускают
весьма наглядную интерпретацию в виде, аналогичном виду обычного
уравнения неразрывности, получаем:
f I ( x I , t I )
J I ( xI , t I ) 0
t I
x I
где – J I ( x I , t I ) k I x I f I bI
соответствующих потоков.
f I
x I
f II ( x II , t II )
J II ( x II , t II ) 0
t II
x II
и J II ( x II , t II ) k II x II f II bII
f II
плотности
x II
Для стационарного состояния:
J , I
df I ( x I )
k
I xI f I ( xI )
dx I
bI
bI
J , II
df II ( x II )
k
II x II f II ( x II )
dx II
bII
bII
Справочно: Данные выражения являются обычными линейными
уравнениями первого порядка, вида: U x f1 ( x)U f 0, которые имеют решения
U C 0 e F f 0 e F e F dx ,
где
F ( x) f 1 ( x)dx
64.
ИССЛЕДОВАНИЕ АСИМПТОТИЧЕСКИХ СВОЙСТВ МОДЕЛИ ПРОЦЕССАОСУШКИ ВОЗДУХА СИЛИКАГЕЛЕМ
Таким образом, получаем:
f ( x1 , x II ) f , I x I f , II x II f x I , x II
k I xI 2
J ,I
C I exp
C 0 , I
bI
2bI
k II x II 2
J , II
C II exp
C
0, II
bII
2bII
k I xI 2
exp
dx
2bI I
k II x II 2
exp
dx
2bII II
(32)
Окончательный вид полученной плотности распределения f(xI,xII)
определяется представленными в выражении (32) интегралами и
постоянными.
Принимая во внимание условие нормировки функций плотности
2
kx
2 b
распределений f∞,I(xI) и f∞,II(xII), с учетом того, что exp
dx
2b k
1 / 2
1 / 2
2 bII
2 bI
находим: C 0 , I
и C 0 , II
k
k II
I
1/ 2
65.
ИССЛЕДОВАНИЕ АСИМПТОТИЧЕСКИХ СВОЙСТВ МОДЕЛИ ПРОЦЕССАОСУШКИ ВОЗДУХА СИЛИКАГЕЛЕМ
Внимание! В результате становится очевидным, что плотности
распределения (31) и (32) совпадают между собой лишь в статистических
условиях динамического равновесия, при J , I J , II 0
С физической точки зрения для стационарных плотностей распределения
f∞,I(xI) и f∞,II(xII), условие J , I J , II 0 эквивалентно допущению не только о
постоянстве полного числа молекул адсорбтива в каждом из
рассматриваемых множеств, но и о постоянстве их относительного
количества в каждом рассматриваемом интервале ( xI , xI dxI ) и ( xII , xII dxII )
В противном случае, при J , I J , II 0 в стационарных условиях адсорбент
должен был бы иметь, либо неограниченную адсорбционную емкость, либо
нулевую эффективность.
Вывод: Для реализации режима параллельного переноса различных
участков стационарных фронтов адсорбции двух независимых множеств
адсорбтива в слое адсорбента плотность соответствующих потоков молекул
адсорбтива в пространстве х каждого из рассматриваемых множеств
должна быть равна нулю J , I J , II 0
66.
ИССЛЕДОВАНИЕ АСИМПТОТИЧЕСКИХ СВОЙСТВ МОДЕЛИ ПРОЦЕССАОСУШКИ ВОЗДУХА СИЛИКАГЕЛЕМ
При этом из (30)-(32) следует, что в анализируемом процессе через
некоторое время, после ввода рассматриваемой системы в слой адсорбента,
устанавливаются предельные стационарные плотности распределения
f∞,I(xI) и f∞,II(xII), вид которых не зависит от начальных плотностей
распределений f0,I=f0,I(S,0) и f0,II=f0,II(S,0).
Замечание: Образно говоря, рассматриваемая система в процессе своей
эволюции через некоторое время, полностью «забывает» свое прошлое, что
является характерной чертой случайных марковских процессов, т.е. систем
не обладающих «памятью».
Вывод: При решении практических задач на асимптотической стадии
эволюции
рассматриваемого
процесса
появляется
возможность
использования решений без начальных условий, задающих исходное
распределение адсорбтива в слое адсорбента, что позволяет существенно
упростить методику инженерных расчетов этих процессов.
67.
ИССЛЕДОВАНИЕ АСИМПТОТИЧЕСКИХ СВОЙСТВ МОДЕЛИ ПРОЦЕССАОСУШКИ ВОЗДУХА СИЛИКАГЕЛЕМ
Применительно к процессам КБА, указанное обстоятельство позволяет
записать для процессов адсорбции каждого i- ого цикла выражение (30) в
виде:
f i f i S Ii , S IIi , t Ii , t IIi f
i
I
S
i
I
, t Ii f
i
II
S
i
II
, t IIi
tI
t II
i
i
i
i
i 2
i
i
i
i
i 2
k I ( S I W I (t I )dt I )
k II ( S II W II (t II )dt II )
1 / 2
1 / 2
i
B Ii
B
0
0
II
CI i
exp
C
exp
II
B Ii
k IIi
B IIi
kI
i
i
здесь WI i и WII i – скорости движения «центров» соответствующих
адсорбционных фронтов в i-ом цикле;
и BIIi BII BIIi 1 - осредненные коэффициенты интенсивности
случайных составляющих в адсорбционных процессах i-ого цикла; при
этом S Ii S S Ii 1 S IIi S S IIi 1
BIi BI BIi 1
S Ii 1 , S IIi 1 и B Ii 1 , B IIi 1
– дополнительное смещение соответствующих
адсорбционных фронтов и изменение интенсивности случайных
составляющих в адсорбционных процессах, обусловленное влияниями во
всех предыдущих циклах, соответственно.
(33)
68.
ИССЛЕДОВАНИЕ АСИМПТОТИЧЕСКИХ СВОЙСТВ МОДЕЛИ ПРОЦЕССАОСУШКИ ВОЗДУХА СИЛИКАГЕЛЕМ
Анализ выражений (33) показывает, что в случае использования процессов
КБА, после завершения всех переходных процессов (t→∞), допустимо
считать: S Ii 1 const и S IIi 1 const
t Ii
t IIi
0
0
В результате, путем замены x Ii S WI i (t Ii )dt Ii и x IIi S WII i (t IIi )dt IIi
при
b
i
I
B I /2
i
и
b
i
II
B
i
II
/2
, выражение (31) для i-ого цикла принимает вид:
f i x Ii , x IIi f i , I x Ii f i , II x IIi f i x Ii , x IIi
2 b i I
CI i
k I
1 / 2
k i I xi I 2
2 b i II
exp
C II i
i
2
b
I
k II
1 / 2
k i II x i II 2
exp
i
2
b
II
(34)
Справочно: Обращаясь к рассмотрению процессов десорбции в
процессах КБА отметим, что время протекания этих процессов
является конечной и относительно малой величиной.
69.
ИССЛЕДОВАНИЕ АСИМПТОТИЧЕСКИХ СВОЙСТВ МОДЕЛИ ПРОЦЕССАОСУШКИ ВОЗДУХА СИЛИКАГЕЛЕМ
При этом использование предельного допущения cW c D 0 , с учетом
i
i
начальных условий, вытекающих из (30) и (31), при t DI t DI
и t DII t DII
позволяет для каждого i-ого цикла представить выражение (26) в виде:
i
i
i
i
i
i
f Di S i , t Di f DI
S DI
, t DI
f DII
S DII
, t DII
t DI
t DII
i
i
i
i
2
i
i
i
i (t DII
)dt DII
)2
( S DI W DI (t DI )dt DI )
( S DII W DII
C DII
0
0
exp
exp
i
i
i
i
i
i
2 B DI t DI
2 B DII t DII
2 B DII
t DII
i
C DI
i
i
2 B DI
t DI
i
(35)
i – скорости движения «центров» соответствующих
здесь WDI i и WDII
десорбционных фронтов в i-ом цикле;
i
i 1
и
BDI
BDI BDI
- осредненные коэффициенты интенсивности
случайных составляющих в десорбционных процессах i-ого цикла; при
i
i 1
i
i 1
S S DII
S S DI
этом S DI
и S DII
i 1
S DI
,
i 1
S DII
и
i
i 1
BDII
BDII BDII
i 1
B DI
,
i 1
B DII
– дополнительное смещение соответствующих
сорбционных
фронтов
и
изменение
интенсивности
случайных
составляющих в десорбционных процессах, обусловленное влияниями во
всех предыдущих циклах, соответственно.
70.
ИССЛЕДОВАНИЕ АСИМПТОТИЧЕСКИХ СВОЙСТВ МОДЕЛИ ПРОЦЕССАОСУШКИ ВОЗДУХА СИЛИКАГЕЛЕМ
В случае использования процессов КБА, после завершения
переходных процессов (t→∞), можно предположить, что: S Ii 1 const
всех
и S IIi 1 const
i
t DI
i
t DII
0
0
i
i
i
i
i
i
i
i (tDII
)dtDII
В результате, выражение (35) путем замены xDI S WDI (tDI )dtDI и xDII S WDII
для i-ого цикла принимает вид:
i
i
i
i
i
i
f Di xDI
, xDII
f i ,DI xDI
f i ,DII xDII
f i ,D xDI
, xDII
C DI
2 B t
i
i
DI DI
i
i
( x DI
( x DII
)2
C DII
)2
exp i i
exp i i
i
i
2
B
t
2 BDII t DII
DI DII
2 BDII t DII
(36)
При температурах точек росы воздуха ниже минус 40оС, при t→∞, учет
влияния участков с небольшим содержанием влаги с→0 в силу (27) и (28)
носит тривиальных характер: c c0 const , где с0 – концентрация паров
воды в газе, подаваемом на регенерацию.
Здесь, как в процессе адсорбции, так и в процессе десорбции имеются
тенденции к неограниченному размыванию сорбционных фронтов, что
способствует равномерному распределению адсорбата по всей длине
адсорбера.
71.
Исследование асимптотических свойств разработанной модели (при t→∞)3
3
Для любого i-ого цикла при t I 2k и t II
, получены решения в виде:
2k II
I
Адсорбционный процесс:
B i
CI iI
kI
1 / 2
i
i
2 BDI
t DI
f
i
S
i
I
, S IIi , t Ii , t IIi f I S Ii , t Ii f II
i
i
S
i
II
, t IIi
i
1 / 2
t II
i
B
BIi C II i II
exp k IIi ( S IIi W II i ( t IIi )dt IIi ) 2
k II
0
BIIi
i
i
i
i
i
i
i
f Di S Di , t D
f DI
S DI
, t DI
f DII
S DII
, t DII
t DI
i
i
i
i ( t DI
exp ( S DI W DI
)dt DI
)2
0
i
i
t Ii
exp k Ii ( S Ii W I i ( t Ii )dt Ii ) 2
0
Десорбционный процесс:
C DI
f
2B
i
i
DI DI
t
t DII
C DII
i
i
i
i ( t DII
exp ( S DII W DII
)dt DII
)2
i
i
2 BDII
t DII
0
i
2B
i
i
DII DII
t
72.
ЛЕКЦИЯ 28. ОСНОВНЫЕ ОПРЕДЕЛЯЮЩИЕ ПАРАМЕТРЫПРОЦЕССОВ КБА
Поскольку распределение (34) остается
неизменным при преобразовании
i
i
i
i i
переменных x I k I x I или x i I x I , а также x i II k IIi x i II или x i II x II
bIi
bIIi
можно говорить, что в рассматриваемом процессе реализуются свойства
статистического самоподобия.
Величины k i I и k i II , с одной стороны выступают в качестве некоторых
масштабных коэффициентов подобия, а с другой стороны в качестве
некоторых
поправочных
множителей,
учитывающих
возможные
отклонения между реальными и модельными процессами.
Таким образом, в представленной модели, на асимптотической стадии
эволюции рассматриваемой iсистемы, с помощью
введения комплексных
i
параметров процесса mi I
bI
kiI
i
и m II
b II
k i II
появляется возможность
учета на эмпирическом уровне не только эффектов, обусловленных
неравновестностью протекающих процессов, но и проявлений, связанных с
их отклонениями от изотермических условий, а также корректировки
других допущений модели.
73.
ОСНОВНЫЕ ОПРЕДЕЛЯЮЩИЕ ПАРАМЕТРЫ ПРОЦЕССОВКБА
Другими словами, рассматривая комплексные параметры m i I и mi II в
качестве некоторой приведенной интенсивности случайных процессов,
характеризующих наличие продольной диффузии, неоднородности
укладки, размера зерна и других свойств адсорбента, флуктуаций и
неравномерностей скорости потока и т.п. можно считать, что она
проявляется как фактор, изменяющий движущую силу адсорбционного
процесса, и тем самым учитывает изменения в интенсивности
массопереноса за счет наличия нестационарных, неравновесных и
неизотермических условий.
С учетом замены
tI
x I S WI (t I )dt I
0
и
t II
x II S WII (t II )dt II
, анализ распределения
0
(29) показывает, что в рассматриваемой системе свойство статистического
самоподобия может проявляться значительно раньше, чем она достигнет
асимптотической стадии своей эволюции. В частности, переход к
подвижным координатам xI и xII дает:
f f xI , xII , t I , t II f I xI , t I f II xII , t II
B
CI e kI tI I (e 2kI tI 1)
kI
1 / 2
k I e 2 k I tI xI 2
k II t II BII
2 k II t II
exp
C
e
(
e
1
)
II
2 kI tI
1)
k II
BI (e
1 / 2
k II e 2 kII tII xII 2
exp
2 k II t II
B
(
e
1
)
II
74.
КБАОСНОВНЫЕ ОПРЕДЕЛЯЮЩИЕ ПАРАМЕТРЫ ПРОЦЕССОВ
e 2 kI tI 1
e 2 kII tII 1
Замена I 2 kI tI , II 2 kII tII и BI 2 I 2 , BII 2 II 2 приводит к выражению:
e
e
kI
k II
f f xI , xII , I , II f I xI , I f II xII , II
1
CI
2
2 I I
1/ 2
2
xI
exp
2
2 I I
1
C
II
2
2 II II
1/ 2
2
x II
exp
2
2 II II
Очевидно, что исходя из (35) и (36), после введения в рассмотрение
i
i
комплексных параметров процесса десорбции в виде mi DI BDI
и mi DII BDII
полученные результаты по аналогии практически без изменений могут
быть распространены и на процессы десорбции.
Вывод: При неизменных свойствах адсорбента, в каждом процессе КБА
появляется возможность описания адсорбционных и десорбционных
фронтов адсорбтива в слое адсорбента в аналогичном виде:
i
i
I
f x ,x
i
D
i
DI
i
II
f x ,x
f x f x f x , x C 2 m
i
DII
i
,I
i
, II
i
II
f x f
i
, DII
i
, DI
i
I
i
DI
i
i
I
i
II
x f x
i
DII
i
,D
i 1 / 2
I
I
i
DI
,x
i
DII
xi I 2
exp
C II 2 mIIi
i
2m I
C DI
i
2 mDI
1 / 2
x i II 2
exp
i
2
m
II
i
i
( xDI
( xDII
)2
C DII
)2
exp
exp
i
i
i
2
m
2 mDII
DI
2mDII
75.
ЗАВИСИМОСТИ ДЛЯ ОПИСАНИЯ ДИНАМИКИ СОРБЦИОННЫХ ФРОНТОВВ результате появляется возможность описания адсорбционных
десорбционных фронтов в пространстве и времени следующим образом:
и
Адсорбция
c c ( S , tC ) cW ( f ( x I )dx I
XI
f (x
II
)dx II )
X II
Десорбция
c D c D ( S , tC ) cW (
f (x
DI
)dx DI
X DI
f (x
DII
)dx DII )
X DII
Комплексные определяющие параметры детерминированных и случайных
составляющих
Адсорбция
m
i
I
Bi I
B i II
i
i ; m II i ; BIi ; BIIi ; k Ii ; k IIi ; C I ; C II
kI
k II
Десорбция
i
i
BDI
; BDII
; C DI ; C DII
76.
Расчетные схемы определения величины динамической активностимелкопористого силикагеля
В процессах с термической
регенерацией
C
B
φ
В процессах КБА
φ
B’
В
С
Фронт адсорбции
Фронт десорбции
Е
A
L0
D
х, м
L
Коэффициент симметричности фронта:
L L0 L
Степень использования адсорбционной
емкости слоя: SBCЕ S ABCD
А’
А
Lа
Е
D
х, м
Lр
Коэффициент симметричности фронтов адсорбции и десорбции:
k р S B'CD S A'B'CD
kа S BCE S ABCD
Степень использования адсорбционной
емкости слоя:
1
Динамическая активность слоя
а Д аР
Даже при бесконечно длинных слоях
силикагеля степень использования его
влагоемкости не превышает 75%
k a La
k p Lp
Динамическая активность слоя адсорбента в
процессах КБА
а Д а р [k p L p ka La ] k p L p a p
В процессах КБА количество влаги, поступившее в адсорбер за полуцикл,
значительно меньше того количества влаги, которое постоянно находится
в слое адсорбента.
77. Функциональная схема экспериментального стенда для исследования процессов подготовки воздуха
I – компрессорная группа;II – блок осушки и автоматики;
IIа
–
секция
ручного
и
полуавтоматического управления
процессами;
IIб – секция полуавтоматического и
автоматического
управления
процессами;
III – блок измерений
1 – фильтр; 2 – компрессор; 3, 15, 27 –
аппарат теплообменный; 4 – клапан
разгрузочный; 5, 46, 47, 48, 49 – клапан
обратный; 6 – ресивер; 7 – глушитель; 8 –
сборник
конденсированной
фазы
загрязнений; 9 – прессостат; 10, 21, 30, 53,
63 – датчик температуры; 11, 20, 57 –
манометр; 12 – клапан предохранительный;
13 – клапан слива конденсата; 14, 23, 25, 33,
38, 62, 65, 67 – вентиль; 16 – фильтрадсорбер;
17,
42,
43
–
фильтр
влагоотделитель; 18, 37, 51, 55, 56 – клапан
редукционный; 19 – усреднитель; 22 –
патрубок для установки контрольных
образцов; 24 – распределительная панель;
26,
31
–
микроманометр;
28
–
быстроразъемные соединения; 29 –
рабочий участок; 32, 36, 50, 54, 58, 60 –
вентиль дроссельный; 34 – термостат; 35 –
пробоотборники; 39 – основной датчик
давления; 40, 41 – клапаны управляющие;
44, 45 – исследуемые образцы; 52, 59, 64 –
датчик давления; 61 – расходомеры
постоянного
перепада
давления
(ротаметры); 66 – расходомеры объемные;
68 – расходомер комбинированный.
77
78. Общий вид универсального экспериментального стенда
Усреднительсекции ручного
управления
Термостат
секции ручного
управления
Блок
осушки и
автоматики
Компрессорна
я группа
78
79. Различные модификации компрессорной группы стенда
Диапазон изменения:объемов ресивера КГ - от 10 до 100 дм3 (по воде)
производительности компрессора от 100 до 500 ндм3/мин
давлений – от 0,1 до 1,0 МПа
расходов воздуха в пределах от 1 до 120 ндм3/мин
Блок осушки и автоматики стенда
Программируемый
блок автоматики и
управления
Секция полуавтоматического и
автоматического управления
79
80. Блок осушки и автоматики стенда
Программируемый блок автоматикиРабочие участки стенда
80
81. Рабочие участки стенда
Общий вид рабочих участковГерметизация контрольных навесок в бюксах
81
82.
Система измерения расхода воздухаСистема измерения влажности воздуха
82
83.
Результаты экспериментальной оценки влагоемкости промышленного мелкопористогосиликагеля марки КСМГ различных поставщиков в статических условиях
0,7
Поставщик №1 (высший сорт)
0,6
Поставщик №2 (высший сорт)
а, (по массе)
0,5
Поставщик №3 (первый сорт)
0,4
Поставщик №4 (импорт)
0,3
0,2
ГОСТ 3956-76. Нижняя
граница силикагеля марки
КСМГ высшего сорта
0,1
ГОСТ 3956-76. Нижняя
граница силикагеля марки
КСМГ первого сорта
0,0
0
0,1
0,2
0,3
0,4
0,5
0,6
0,7
0,8
0,9
Р/Р
1s
1. Влагоемкость промышленного мелкопористого силикагеля марки КСМГ
различных поставщиков в статических условиях при относительной влажности
воздуха менее 50% может отличаться более чем на 100%.
2. Использование нормативных осредненных характеристик влагоемкости
промышленного мелкопористого силикагеля следует признать не эффективным.
84.
Результаты определения средней влагоемкости силикагеля марки КСМГв статических условиях
При различных давлениях
0,50
0,50
0,45
0,45
0,40
0,40
0,35
0,35
а, (по массе)
а, (по массе)
При различных температурах
0,30
0,25
0,20
0,30
0,25
0,20
0,15
0,15
0,10
0,10
0,05
0,05
0,00
0
0,2
16,3 оС
0,4
22,5 оС
0,6
30,6 оС
0,8
Р/Р1s
40,2 оС
0,00
0
0,2
0,1 МПА
0,4
0,6
0,2 МПа
0,8
Р/Р1s
0,6 МПа
1. При постоянной относительной влажности воздуха влагоемкость
мелкопористого силикагеля можно считать приблизительно постоянной вне
зависимости от температуры, при которой происходит процесс поглощения.
2. В исследуемом диапазоне рабочих давлений установок влагоемкость
мелкопористого силикагеля практически не зависит от давления среды.
85. Результаты определения динамической активности слоя силикагеля с термической регенерацией и в процессах КБА при различных
температурах окружающей среды25
С термической регенерацией
силикагеля [по данным Кельцева]
20
Расчет с помощью предложенной
модели для термической регенерации
силикагеля
аД, (% по массе)
Расчет с помощью предложенной
модели в процессах КБА
15
Эксперимент, термическая
регенерация силикагеля (весовой
метод)
10
По выходным кривым для
термической регенерации силикагеля
Эксперимент, процессы КБА (весовой
метод)
5
С термической регенерацией
силикагеля [по данным Глизманенко]
0
10
15
20
25
30
35
40
t, оС
1. В процессах КБА динамическая активность слоя силикагеля более чем в 3 раза
отличается от его динамической активности в процессах с термической
регенерацией.
2. Применение данных по динамической активности силикагеля, используемых в
расчетах процессов с термической регенерацией, к процессам КБА приводит к
некорректному определению ресурсных характеристики установок.
86.
Нахождение определяющих комплексов моделиkI
3
1
1
2t cI 2t cI / 3 t cI
m
k II
3
1
1
2t cII 2t cII / 3 t cII
m i II
i
I
Bi I
i
kI
B i II
i
k II
BIi ( S , t ) 2 DI /(1 N
da
) const
dc
i
BDI
( S , t ) 2 DDI /(1 N
0,12
da
) const
dc
BIIi ( S , t ) 2 DII /(1 N
da
) const
dc
i
BDII
( S , t ) 2 DDII /(1 N
da
) const
dc
0,08
0,1
0,06
S, м
S, м
0,08
0,06
0,04
1
4
7
10
0,02
0
а)
0
30
60
90
120
2
5
8
3
6
9
0,04
1
4
7
10
0,02
0
150
180
210
t‘I, с
240
б)
0
30
60
90
120
150
2
5
8
180
3
6
9
210
t‘
240
II, с
Результаты экспериментального исследования кинетической стадии эволюции каждого множества адсорбтива: а)
ϕ=25%, б) ϕ=75%, расчет 1-5 , эксперимент 6-10 при расходах воздуха: 10, 30, 50, 75 и 100 ндм3/мин
0,005
0,01
0,004
0,0035
1
2
3
1
4
2
3
kI≈ kII≈ const ≈ 0,0155 1/с
4
0,003
0,005
а)
Для процессов с термической
регенерацией силикагеля
0,0045
0,015
k, 1/с
k, 1/с
0,02
0
20
40
Q,
60
ндм3/мин
80
100
б)
0
20
40
60
80
100
Q, ндм3/мин
Оценка величины k, для процессов: а) с термической регенерацией, б) КБА,
при величинах контрольной влажности: 1 – 25 %, 2 – 50%, 3 – 75%, 4 – среднее значение
Для процессов КБА
kI≈ kII≈ const ≈ 0,0045 1/с
87.
1,40E-031,40E-03
1,20E-03
1,20E-03
1,00E-03
1,00E-03
D0, м2/c
D0, м2/c
Определение величин, характеризующих интенсивность случайных
составляющих
8,00E-04
6,00E-04
4,00E-04
а)
100
200
300
400
3
1
2
2,00E-04
0,00E+00
0
6,00E-04
4,00E-04
1
2
2,00E-04
8,00E-04
500
Red
0,00E+00
б)
0
0,1
0,2
0,3
0,4
W0, м/с
0,5
Результаты определения величин интенсивности случайных составляющих DI , DII , DDI, DDII в зависимости от
а) числа Рейнольдса, б) скорости, 1, 2 – в процессах адсорбции и десорбции соответственно, 3 – теоретическая
зависимость
Адсорбция
DI DII 2 10 6 Re d 3 10 6
Десорбция
DDI DDII 8 10 6 Re d 1 10 5
Di dчW0 2 Dэ
где dч – средний диаметр частиц силикагеля,
W0 – средняя скорость потока воздуха в слое адсорбента,
Dэ – эффективный коэффициент диффузии
Интенсивность случайных составляющих адсорбционных и десорбционных
процессов в конденсационно-адсорбционных установках на основе процессов
КБА в основном определяется гидродинамикой соответствующих потоков.
88. Адекватность модели и границы ее применения
10,9
0,8
с(S,tc)/cw
0,7
1
2
3
4
5
6
7
8
0,6
9
10
0,5
11
12
0,4
13
14
15
16
0,3
0,2
0,1
0
0,03
0,13
0,23
0,33
0,43
0,53
S, м
0,63
ндм3/мин
Динамика адсорбционных фронтов при расходах воздуха 30, 50, 75, 100
и времени адсорбции
300с – модель 1-4; эксперимент 9-12; при времени адсорбции 21600с – модель 5-8; эксперимент 13-16
1. Возможность использования в модели осредненных характеристик протекающих
процессов.
2. При малых расходах воздуха и продолжительности адсорбционного процесса
расхождение между экспериментальными и расчетными значениями не
превышают 10%.
3. В диапазоне изменения относительной влажности от 30% до 70%, по мере
увеличения продолжительности адсорбционного процесса от 300 с до 6 ч и расхода
воздуха, максимальное расхождение увеличивается до 25%, что не оказывает
существенного влияния на нахождение определяющих параметров.
89. Результаты исследования условий обеспечения устойчивости сорбционных фронтов в процессах КБА
Избыточный объем воздуха,подаваемого на регенерацию
Недостаточный объем воздуха,
подаваемого на регенерацию
1
IIд
0,2
0 Iд
а) 0
0,05
0,1
0,6
IIд
0,2
0
с(S,tc)/cw
0,8
с(S,tc)/cw
0,8
0,4
Iд
б) 0
IVд
0
0,1
0,2
0,1
0,15
S,0,2м
0,6
IIa
Iд
IIд
0,4
Iа
0,2
0,2
а) 0
0,03
0,06
0,09
S,
м
0,12
1
IIIа
0,6
0,4
S, м
0,8
IVа
IVд
IIа
IIIд
б) 0
а) Q=30 л/мин; б) Q=100 л/мин;
Индексы «а» и «д» соответствуют процессам
адсорбции и десорбции;
I - при длительности 1 цикл;
II - при длительности 5 циклов;
III - при длительности 100 циклов;
IV - при длительности 200 циклов.
0,6
Iд
IIa
IIд
0,4
Iа
0,2
IIд
0
0,05
0,8
0
0
а)
S, м
IIa
IVа
IIд
0,2
1
Iа
IIIд
IIа
0,4
1
0,6
IIIа
с(S,tc)/cw
IIa
0,4
0,8
0
0,2
0,4
0,6
S,0,8
м
б) 0
0,05
0,1
0,15
S,
м
0,25
0,2
Изменение влажности воздуха в процессе регенерации
100%
95%
90%
φ
0,6
Iа
1
с(S,tc)/cw
0,8
с(S,tc)/cw
с(S,tc)/cw
1
Расчетный объем воздуха,
подаваемого на регенерацию
85%
80%
75%
70%
40
60
80
100
120
140
160
t, с
180
При длительностях менее 80-100 с эффективность процесса регенерации снижается на
столько сильно, что не может быть компенсирована используемыми коэффициентами
запаса, что неминуемо приведет к потере устойчивости сорбционных фронтов
89
90. Эксплуатационные изменения свойств силикагеля в процессах КБА
11
0,8
1
2
3
4
0,6
0,6
0,4
0,4
0,6
0,2
0,2
0
0
0
S, м
0,2
Изменение конфигурации сорбционных фронтов в
зависимости от качества применяемого силикагеля
модель 1-2, эксперимент 3-4,
при а=11 г/100г и а=7 г/100г
1
0,1
1
2
3
4
0,8
с(S,tc)/cw
0,3
0,4
S, м
Изменение конфигурации сорбционных фронтов в
Изменение конфигурации сорбционных фронтов в
зависимости от качества силикагеля и температуры
зависимости от температуры
t=25оС: модель 1-2, эксперимент 5-6, при а=11 и 7 г/100г
модель 1-2, эксперимент 3-4,
t=40оС: модель 3-4, эксперимент 7-8, при а=11 и 7 г/100г
при t=25оС и t=40оС
0
0,3
0,6
0,4
0,2
0,2 S, м 0,3
0,4
0,1
0,2
1
2
3
4
0,8
0,6
0,4
0,2
0
0
а)
0
1
с(S,tc)/cw
0,1
2
4
6
8
0,4
0,2
0
1
3
5
7
0,8
с(S,tc)/cw
с(S,tc)/cw
0,8
2
4
с(S,tc)/cw
1
3
1
0
0,1
S, м
0,2
0,3
б)
0
0,2
S, м
0,4
0,6
Изменение сорбционных фронтов паров воды на мелкопористом силикагеле после его загрязнения маслом при температуре t=40 оС
а) Q=30 л/мин, б) Q=100 л/мин, расчет с помощью разработанной модели 1-2, эксперимент 3-4 при а=11 г/100г и а=7 г/100г
Сочетание повышенной температуры протекающих процессов и низкого качества силикагеля
проявляется в процессах КБА не столько в виде снижения его динамической активности,
сколько в аномальном поведении начального участка фронта адсорбции первого множества
адсорбтива, что может приводить к нерасчетному увеличению длины работающего слоя
более чем в 1,5 раза
90
91. Изменение адсорбционной способности силикагеля в процессах КБА
1t=1 мес. теор.
t=3 мес. теор.
t=5 мес. теор.
t=9 мес. теор.
t=13 мес. теор.
t=17 мес. теор.
t=1 мес. эксп.
t=3 мес. эксп.
t=5 мес. эксп.
t=9 мес. эксп.
t=13 мес. эксп.
t=17 мес. эксп.
0,9
Cм, % (по массе)
0,8
0,7
0,6
0,5
0,4
0,3
0,2
0,1
0
t=2 мес. теор.
t=4 мес. теор.
t=7 мес. теор.
t=11 мес. теор.
t=15 мес. теор.
t=18 мес. теор.
t=2 мес. эксп.
t=4 мес. эксп.
t=7 мес. эксп.
t=11 мес. эксп.
t=15 мес. эксп.
t=18 мес. эксп.
0
0,1
0,2
0,3
0,4
0,5
S00,6
”, м
Распределение паров масла по мелкопористому силикагелю марки КСМГ при различной длительности насыщения им, расчет с помощью
разработанной модели 1-18; эксперимент 19-36 при длительности насыщения маслом: 1, 2, 3, 4, 5, 7, 9, 11, 13, 15, 17, 18 месяцев соответственно
S0
МCМ
F (1 ПУКЛ ) П З М
а I a I (1
Vобр
kМ C М
Vобр )
VA М
где S0”– текущее положение «центра тяжести»;
αМ ~0,3 – коэффициент необратимого сорбирования следов
компрессорного масла;
СМ ~ 0,03 г/м3 – средняя концентрация следов масла на выходе
из компрессора;
Vобр – объем обработанного воздуха;
F – площадь поперечного сечения адсорбера;
ПУКЛ – средняя пористость слоя засыпки зерен силикагеля;
ПЗ – средняя пористость зерен силикагеля;
ρМ – средняя плотность следов компрессорного масла.
аI′ – текущая величина адсорбции в первой точке перегиба;
аI – исходная величина адсорбции в первой точке перегиба;
kМ – постоянный коэффициент;
VА – объем адсорбера.
Загрязнение силикагеля следами компрессорного масла и продуктов его разложения
приводит к резкому увеличению средней скорости распространения первого множества
адсорбтива по слою адсорбента, что приводит не только к смещению, но и деформации
сорбционных фронтов
91
92. Влияние термодинамических параметров на эффективность контроля и дозировки объемов воздуха в процессах КБА
1,141,12
Сухой ресивер
Мокрый ресивер
1,12
1,10
1,08
m“’
m
1,08
1,06
1,06
1,04
1,04
1,02
1,02
1,00
а)
Сухой ресивер
Мокрый ресивер
1,10
0
50
3/мин
100 Qп+Qр, ндм150
1,00
б)
0
50
100
Qп, ндм3150
/мин
Изменение показателя политропы а) в процессах расширения, б) в процессах сжатия
Для процессов расширения
0.0451
Сухой ресивер m m 0,9005 (Qп Q p )
Для процессов сжатия
0, 026
Сухой ресивер m 1,1679 Qп
Мокрый ресивер m m 1,0009 0,0003 (Qп Q р )
25%
20%
40%
Сухой ресивер
Мокрый ресивер
Мокрый ресивер m 1,0318 0,0002 Q р
29%
Сухой ресивер
Мокрый ресивер
30%
19%
15%
20%
10%
14%
10%
9%
5%
0%
а) 0
Сухой ресивер
Мокрый ресивер
24%
0%
50
Qп, ндм3/мин
100
150
б)
0
50
Qп, ндм3/мин
100
150
4%
в) 0
20
40
60
ндм3/мин
80 Qп,100
120
Ошибка в определении а) расхода воздуха в объекты, б) расхода воздуха на регенерацию, в) производительности компрессора
Установлено, что использование коэффициента запаса в зависимостях по определению объема
воздуха, подаваемого на регенерацию, на уровне 1,05-1,08 обеспечивает устойчивую и
эффективную работу установок на основе процессов КБА на всех расчетных режимах
92
93. Влияние негативных факторов на высоту работающего слоя силикагеля
а)б)
а) в зависимости от влагоемкости силикагеля в первой точке перегиба изотермы адсорбции паров воды на силикагеле;
б) в зависимости от рабочих температур
В качестве одних из основных определяющих физико-химических параметров, влияющих на надежность и
безопасность технологических процессов, можно выделить температуру протекающих процессов и
статическую влагоемкость силикагеля в первой точке перегиба изотермы адсорбции.
Вероятность возникновения внезапных, непрогнозируемых отказов в конденсационно-адсорбционных установках с
использованием процессов КБА, связанных с повышением влажности воздуха на их выходе, существенно
возрастает в результате нерасчетного снижения адсорбционной способности силикагеля в сочетании с повышенной
температурой осушаемого воздуха, особенно в случае применения адсорберов малой длины.
93
94. Усовершенствованная функциональная схема конденсационно-адсорбционной установки в составе КСУ на основе процессов КБА
I – компрессорная группа, II – блокосушки и автоматики, III – блок
измерений, IV - блок выносной
сигнализации;
1 – фильтр; 2 – компрессор; 3, 14 –
аппарат теплообменный; 4 – клапан
разгрузочный; 5, 24, 25, 26, 27 – клапан
обратный; 6 – основной ресивер; 7 –
глушитель;
8
–
сборник
конденсированной фазы загрязнений; 9 –
прессостат; 10, 32, 43, 47 – манометр; 11 –
клапан предохранительный; 51, 52 –
датчик температуры; 12 – клапан слива
конденсата; 13, 33, 40 – вентиль; 15, 19, 20
– фильтр влагоотделитель; 16, 30, 41–
датчик давления; 17, 18, 35 – клапан
управляющий; 21 – быстроразъемные
соединения; 22, 23 – адсорберы; 28, 36,
44, 48 – вентиль дроссельный; 29, 31, 34,
42, 46 – клапан редукционный; 37, 45 –
индикатор расхода воздуха; 38, 53 –
датчик влажности; 39 – компенсационный
ресивер; 49 – индикатор аварийного
расхода воздуха; 50 – блок автоматики;
54 – персональный ЭВМ.
94
95.
Расчет характеристик основных комплектующих изделий КГ установок95
96.
Расчет характеристик основных комплектующих изделий БОА установок96
97. Инженерная методика расчета адсорбционных установок подготовки воздуха для надежного и безопасного содержания объектов под
избыточным давлениемРасчет адсорбционных установок производится в три этапа:
I. Расчет основных технологических характеристик оборудования установок
II. Расчет и определение характеристик управления, регулирования и контроля режимами и
циклами установок
III. Оценка параметров устойчивости сорбционных фронтов процессов КБА и времени
экспозиции отказов установки
Исходные данные для расчета:
Термодинамические параметры:
Технологических процессов:
• параметры расчетных нормальных условий работы установки Tн.у, K; Pн.у, Па; ρн.у, кг/м3;
• абсолютная влажность воздуха на входе свх и выходе свых адсорберов установки;
• максимальная рабочая температура Tmax и диапазон ее изменения ΔT= Tmax- Tmin K;
• максимальное рабочее давление в цикле работы компрессора Pmax и диапазон его изменения
ΔР= Рmax- Рmin Па;
• максимальное рабочее давление в цикле работы адсорберов Pадmax и диапазон его
изменения ΔРад= Радmax- Радmin Па;
Рабочих помещений установки:
• диапазон изменения относительной влажности воздуха Δϕр ;
• максимальная температура окружающей среды Tо/сmах и диапазон ее изменения ΔTо/с= Tо/сmaxTо/сmin K;
97
98. Инженерная методика расчета адсорбционных установок подготовки воздуха для надежного и безопасного содержания объектов под
избыточным давлениемРасходные характеристики:
• максимальная производительность компрессора Qк и диапазон ее изменения ΔQк=
Qкmax- Qкmin нм3/c ;
• максимальный расход осушенного воздуха QП и диапазон его изменения ΔQП=
QПmax- QПmin нм3/c ;
• максимальный расход осушенного воздуха, подаваемого на регенерацию Qр и
диапазон его изменения ΔQр= Qрmax- Qрmin, нм3/c;
Технологические параметры:
• относительная продолжительность включения компрессора ПВ;
• предельно допустимое число включений компрессора NК;
• расход компрессорного масла в установившемся тепловом режиме см и диапазон
его изменения Δсм= смmax- смmin г/м3;
• насыпная плотность применяемого силикагеля ρN, кг/м3;
• пористость засыпки адсорбента П;
• средний диаметр зерен применяемого силикагеля dч, м;
• фактическая изотерма адсорбции паров воды на применяемом силикагеле а=f(ϕ),
% (масс);
98
99. Расчет характеристик основных комплектующих изделий КГ установок (часть 1)
1. Исходя из заданного предельно допустимого количества включений компрессор (вчас) и известного соотношения ПВ = τРК/(τРК+τПК), где τРК и τПК - время работы и простоя
компрессора соответственно, находим минимально допустимую величину
длительности цикла работы компрессора:
τцк = (τРК+τПК) =3600/ NК
2. Определяем время работы компрессора: τРК =ПВ · τцк
3. Вычисляем время простоя компрессора:
τПК=(1- ПВ) · τцк
4. Находим максимальный объем воздуха (при нормальных условиях), подаваемый в
кабели связи за цикл работы компрессора: VПmax = QП · τцк
5. Вычисляем максимальный объем воздуха, необходимый для регенерации
адсорбента каждом цикле, по формуле:
VPmax = Pн.у · VПmax /(Pср - Pн.у), где Pср= (Pmax+ Pmin)/2 – среднее давление в цикле.
6. Оцениваем время регенерации адсорбента и проверяем выполнение условий для ее
эффективной реализации: τРА = τПК – τКП ≥120,
где τКП ~ (60 с) – время необходимое для контроля расхода воздуха, подаваемого в
кабели связи.
100. Расчет характеристик основных комплектующих изделий КГ установок (часть 2)
7. Определяем максимальный расход воздуха (при нормальных условиях), подаваемыйна регенерацию адсорбента:
QР= VPmax / τРА
8. Оцениваем максимальный расход воздуха (при нормальных условиях) в цикле:
Qmax = QП + QР
9. Вычисляем минимальный объем ресивера КГ (по воде):
VКГ = Pн.у · (Qmax · τРА + QП· τКП )/(Pmax -Pmin)
10. Определяем минимальную производительность компрессора (при нормальных
условиях):
QК = VКГ · (Pmax - Pmin)/ (Pн.у· τРК )
11. С помощью полученных данных по известным методикам производим расчет
теплообменного аппарата КГ.
12. На основании полученных результатов осуществляем подбор серийных
комплектующих изделий КГ установок.
101. Расчет характеристик применяемого оборудования БОА (часть 1)
1. Рассчитываем минимально допустимую площадь поперечного сечения Smin идиаметр адсорбера DА:
4S min
Smin= Qmax· Pн.у/( Pср ·П· Wmax);
DA
где Wmax – средняя максимально допустимая скорость потока в процессе адсорбции
(~0,3 м/с).
2. Оцениваем максимальный объем воздуха, обрабатываемого за один цикл:
V Цmax = V Пmax+ VPmax
3. Оцениваем максимальную массу влаги, содержащуюся в объеме воздуха,
обрабатываемого за один цикл:
M Цmax= V Цmax· аВ,
где аВ – абсолютная влажность воздуха при максимальной температуре, кг/м3
4. Находим минимально допустимую массу применяемого силикагеля:
M С = M Цmax/ а,
где а ~ (0,04 кг/кг) – минимально допустимая исходная динамическая активность
силикагеля
5. Определяем минимальный объем слоя силикагеля в адсорбере:
VАmin = M С/ ρN
102. Расчет характеристик применяемого оборудования БОА (часть 2)
6. Вычисляем минимально допустимую высоту слоя силикагеля и проверяемвыполнение условий для его эффективного использования:
HCmin = VАmin/ Smin
7. Определяем минимальную расчетную высоту слоя силикагеля:
HРmin = HCmin+ S0 ≥ Lmin,
где S0 – конечное значение глубины проникновения адсорбтива в кинетическом
процессе, включая высоту неработающего слоя,
S 0 Re d 10 4 0,0637 0,0404 , Lmin ~ (0,6 м) – предельная высота работающего
слоя силикагеля в рассматриваемых условиях.
8. По найденному значению DА с учетом серийных комплектующих находим
фактическое значение DАР ≥ DА и производим корректирующий расчет адсорберов.
9. Определяем фактический объем адсорбера:
2
DAP
Vф
H P min
4
103. Расчет характеристик применяемого оборудования БОА (часть 3)
10. Находим фактическую массу засыпки силикагеля:МСф=Vф·ρN,
11. Вычисляем фактический максимальный объем воздуха, обрабатываемого за один
цикл:
V ЦФmax = V Цmax+Vф·(Pmax / Pн.у.)
12. С полученными значениями повторяем расчет по пунктам 1-7.
13. Находим предельный уровень насыщения силикагеля маслом в адсорберах для
аМ ~ 0,18 (по массе):
ММ = 2МСф· аМ
14. Вычисляем предельный объем воздуха подаваемого в кабели связи:
VПmax = ММ/( αМ СМ)
где СМ ~ 0,03 г/м3 – расчетная концентрация следов масла на выходе из компрессора,
а αМ ~0,3 - коэффициент необратимого сорбирования следов компрессорного масла.
15. Оцениваем минимальное время работы адсорберов БОА.
τзд = VПmax / Qmax > 1года
16. На основании полученных результатов осуществляем подбор серийных
комплектующих изделий БОА установок.
104. Блок-схема методики определения исходных данных для разработки процессов управления, регулирования и контроля
104105. Я не сумел списать на экзамене «ТЕПЛОМАССООБМЕН В БИОСФЕРЕ»
Я НЕ СУМЕЛ СПИСАТЬ НА ЭКЗАМЕНЕ«ТЕПЛОМАССООБМЕН В
БИОСФЕРЕ»





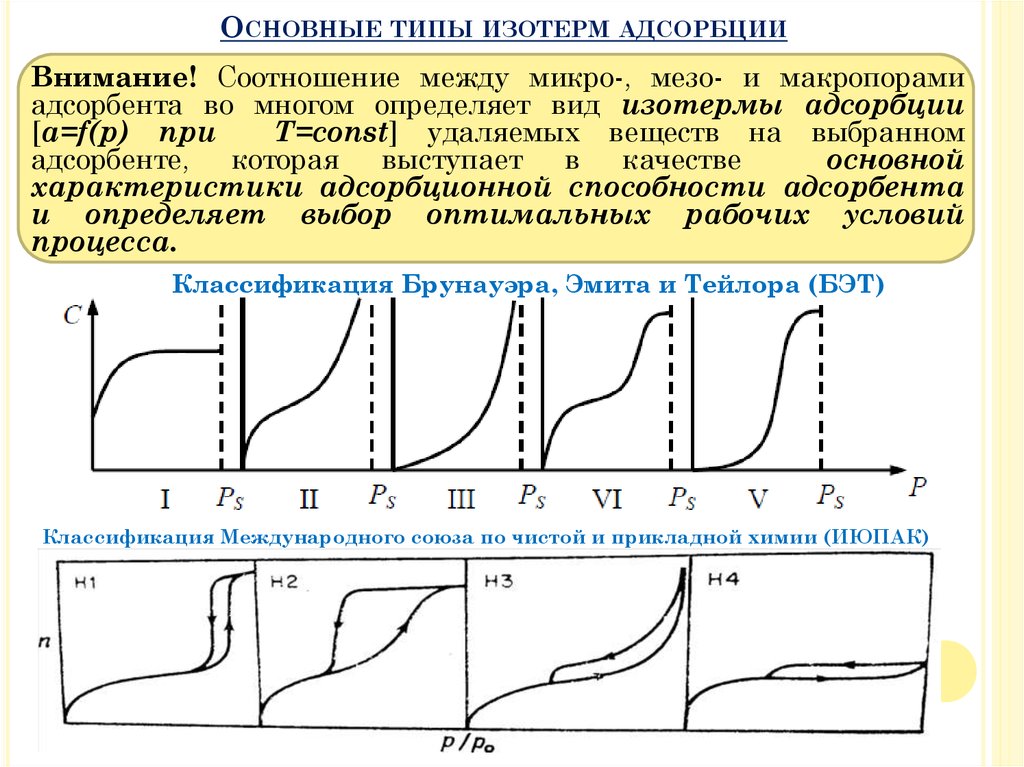
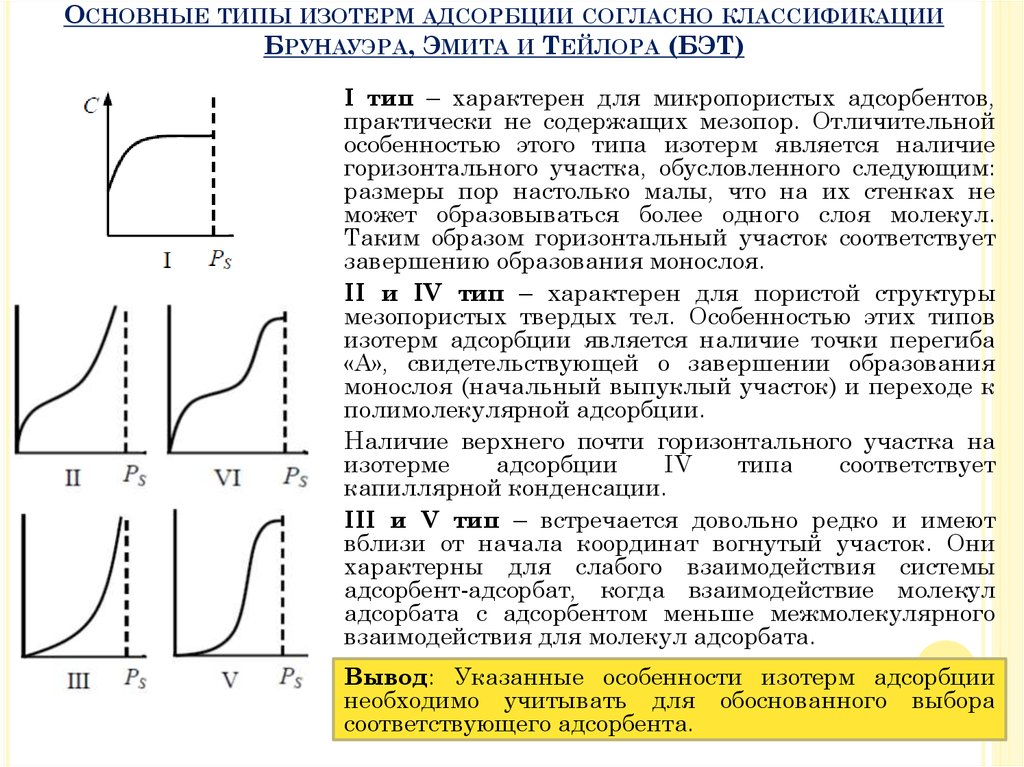
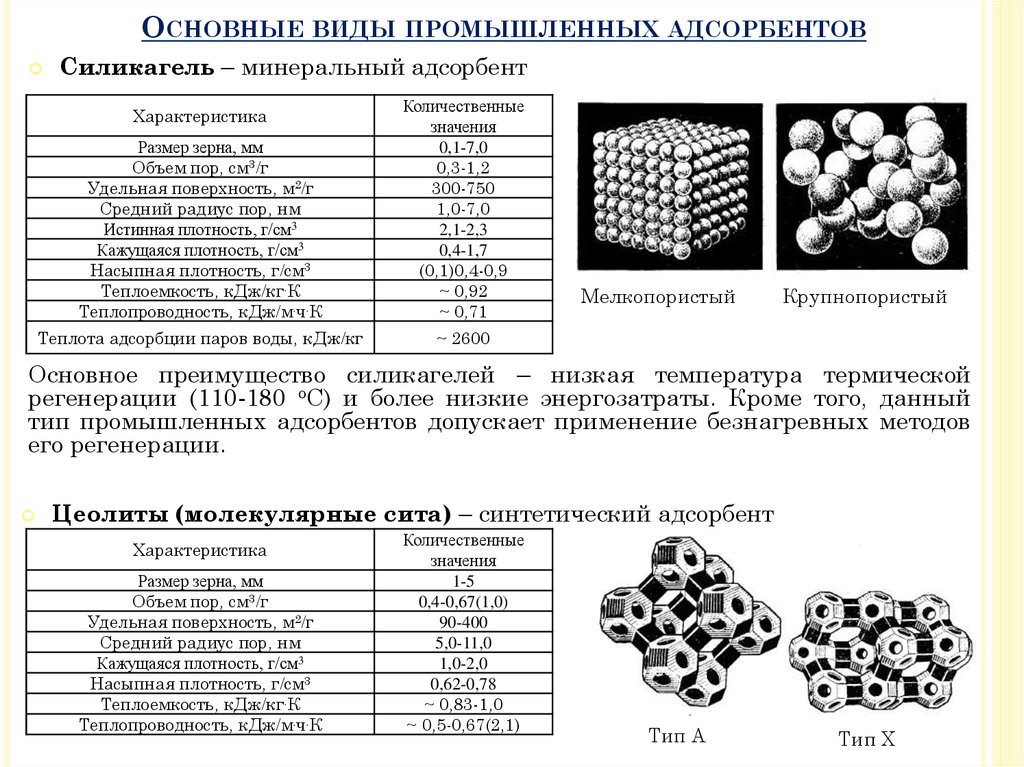
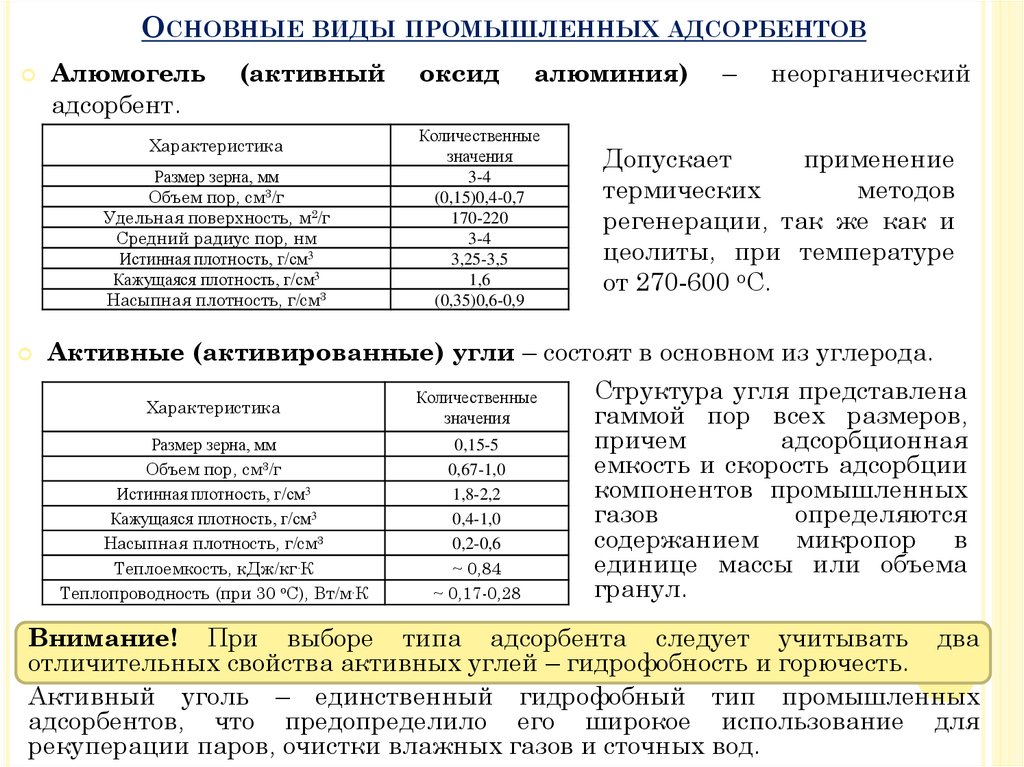
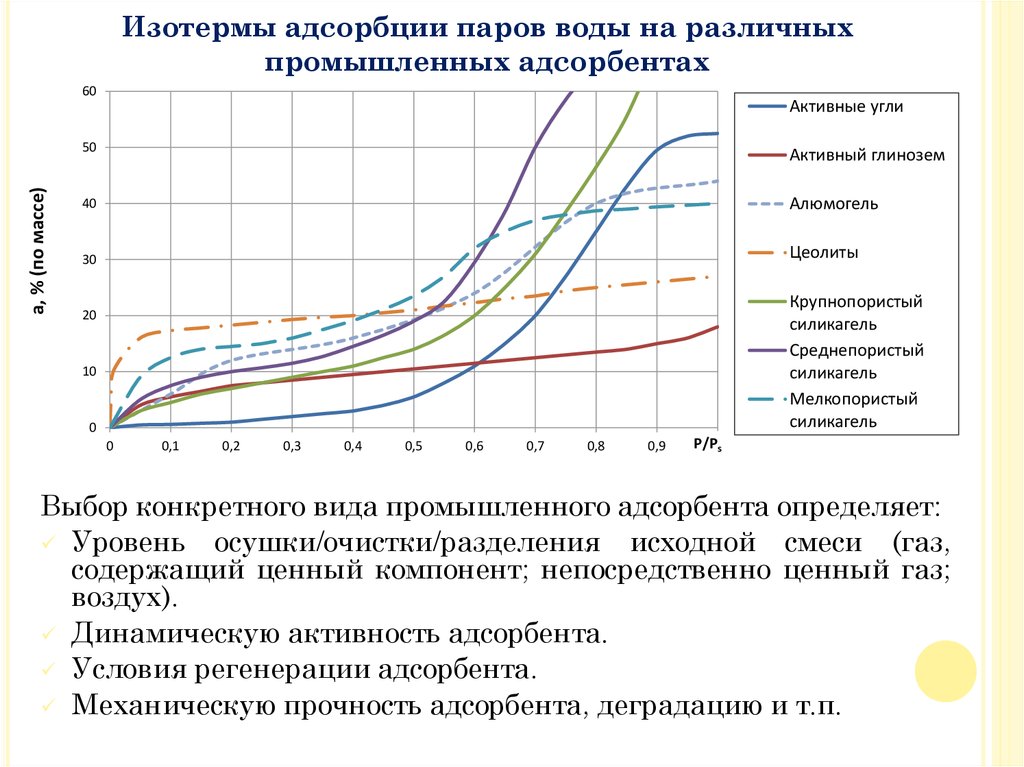
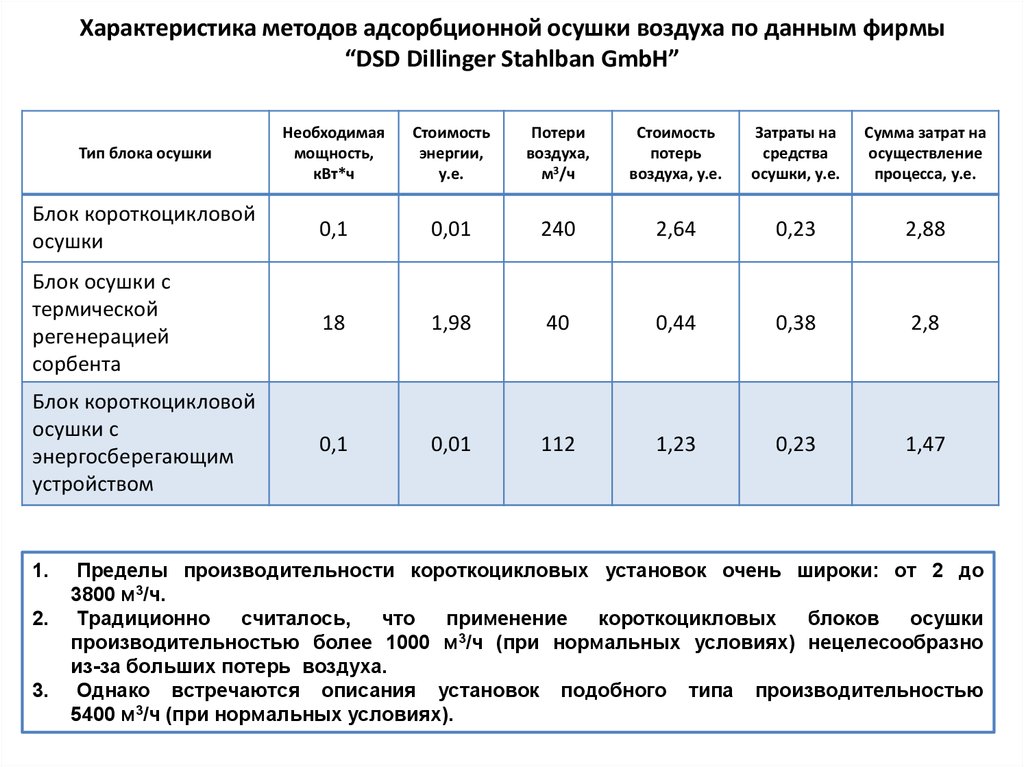








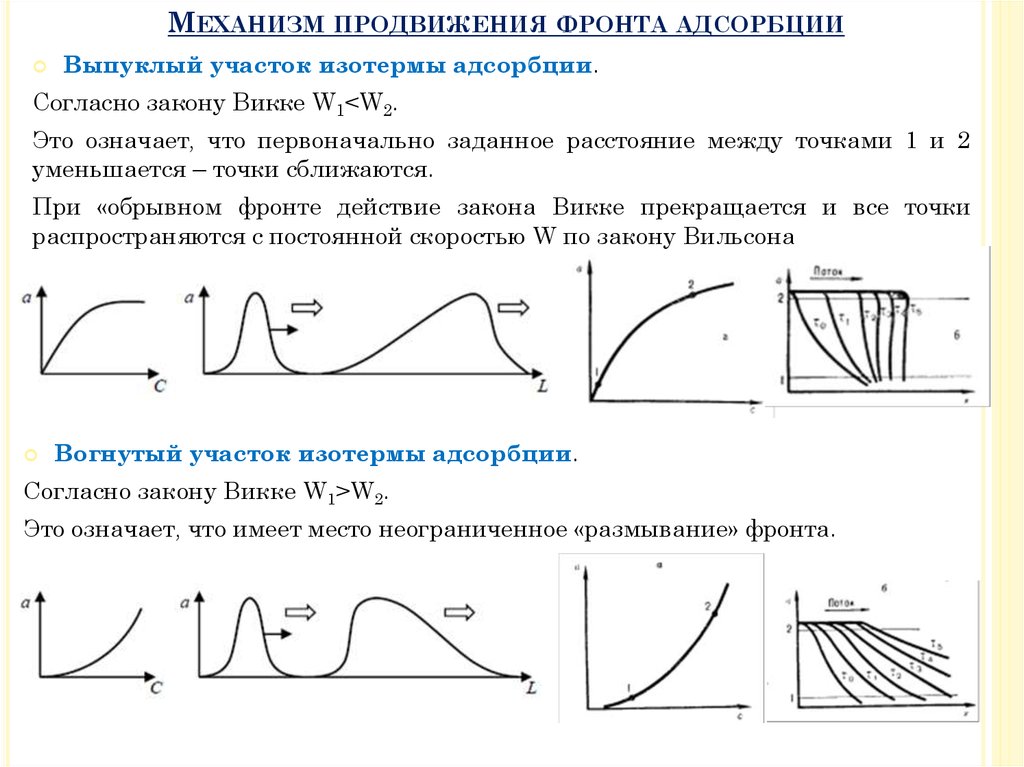






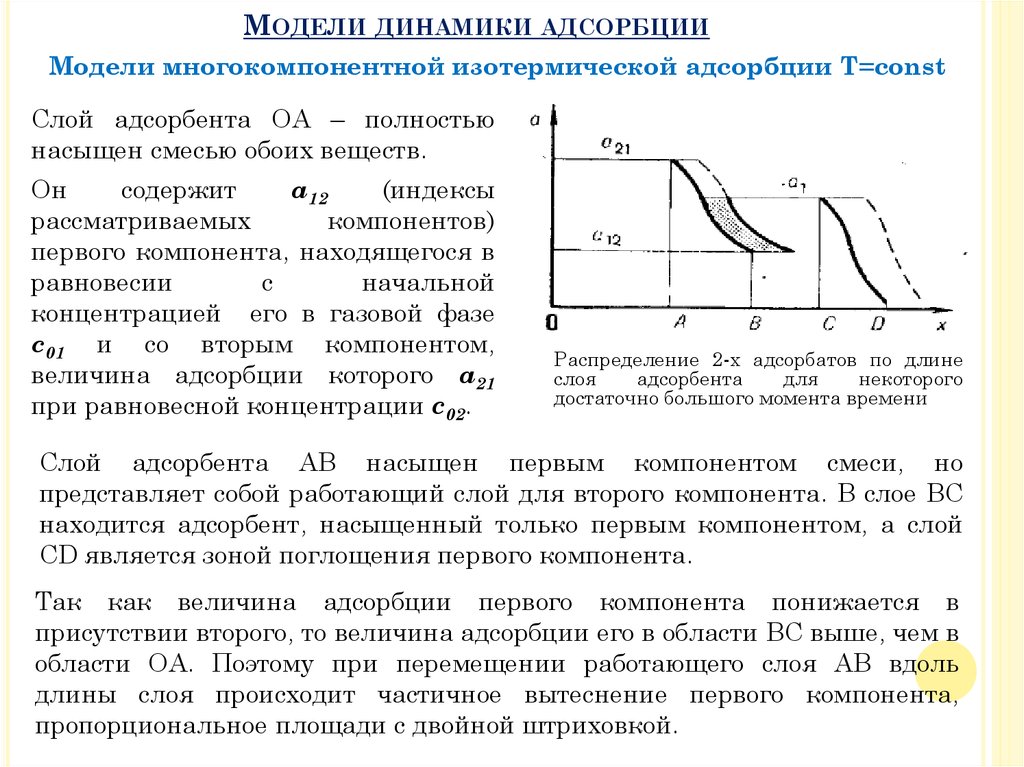











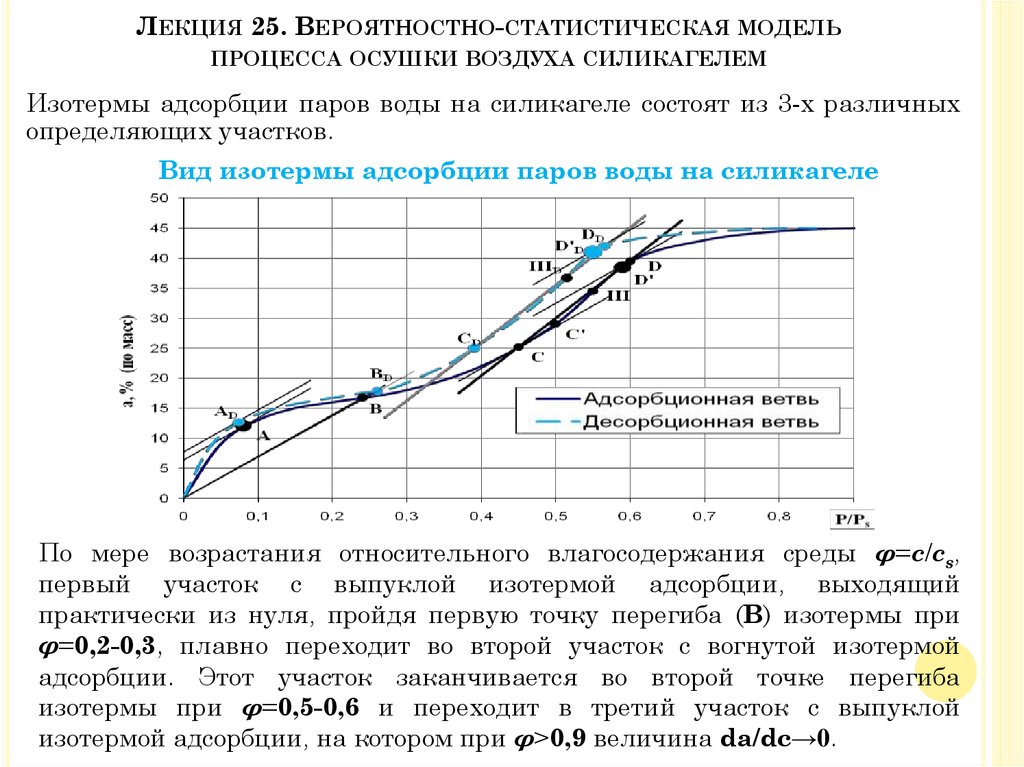

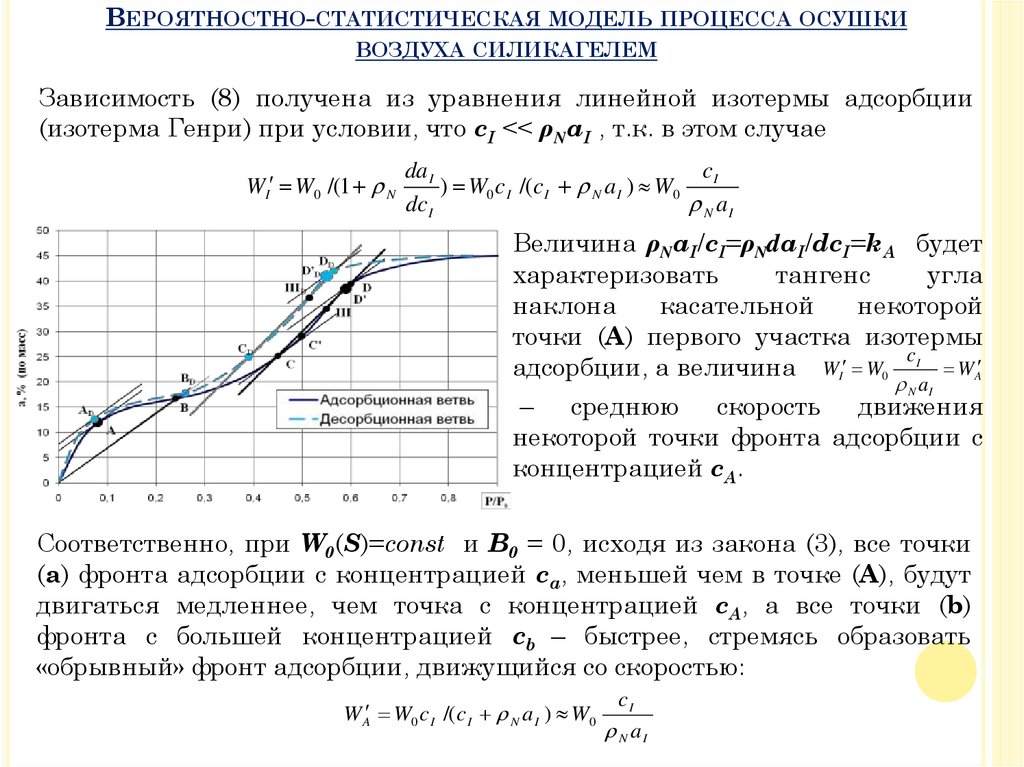
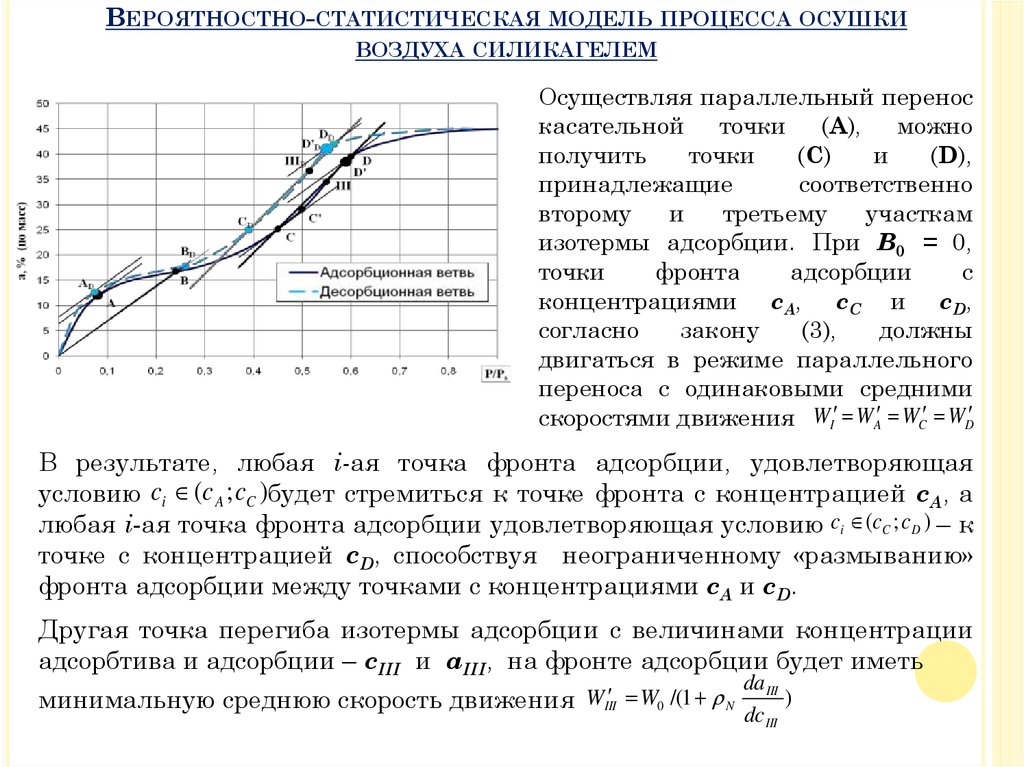
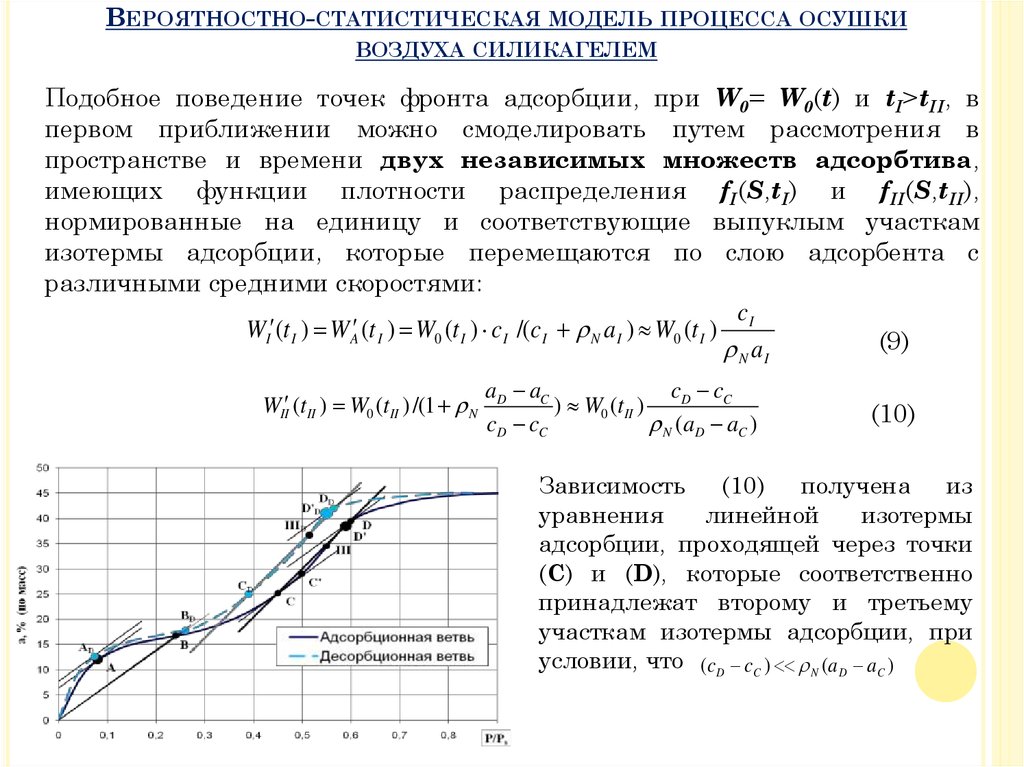
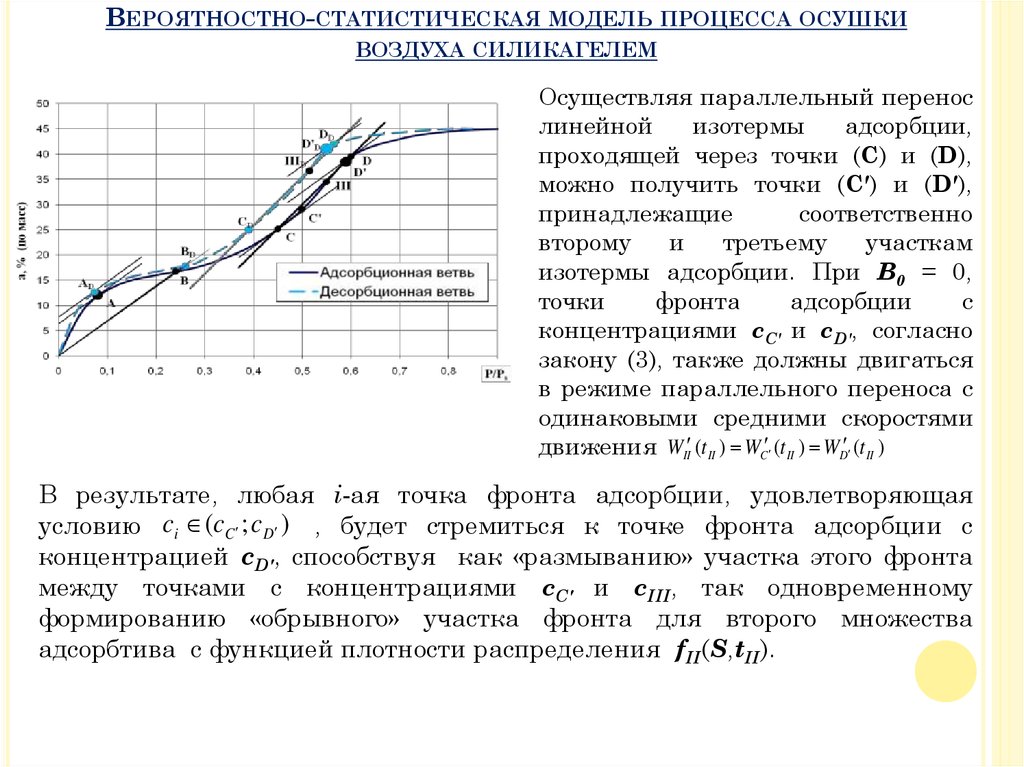
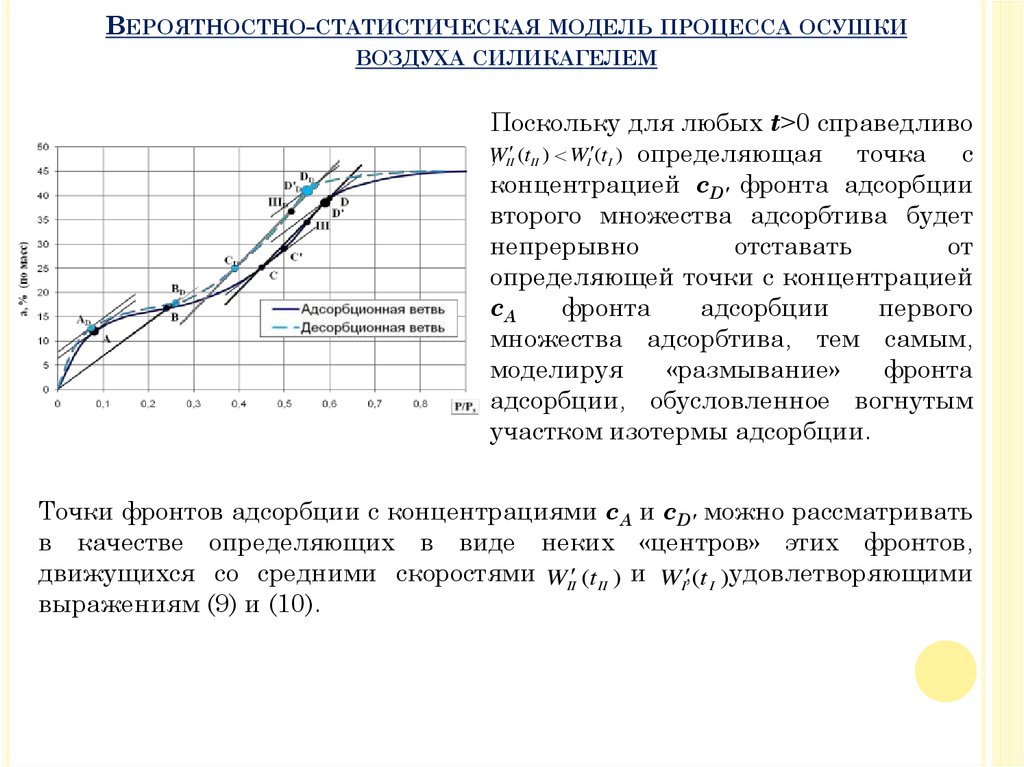












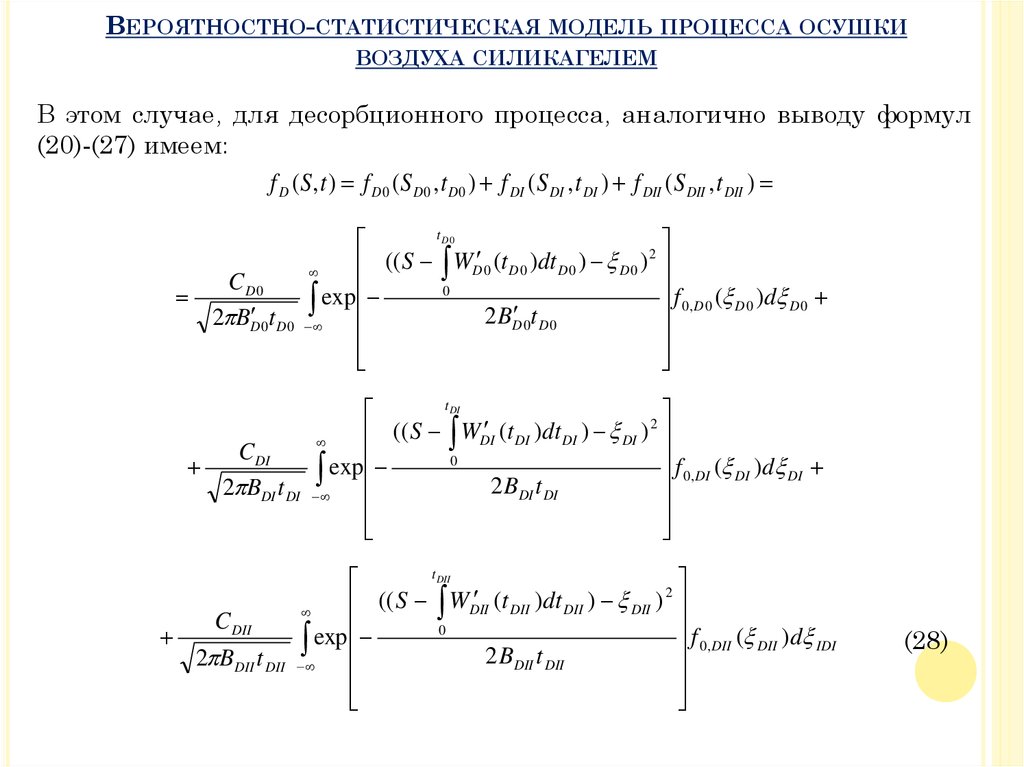
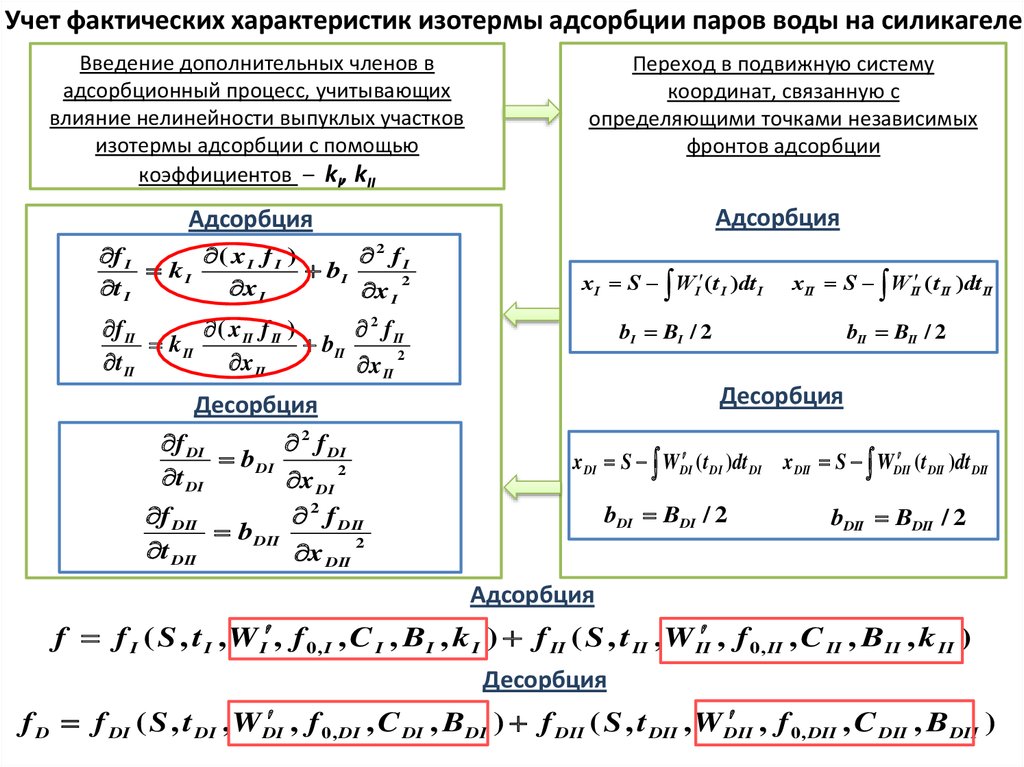

















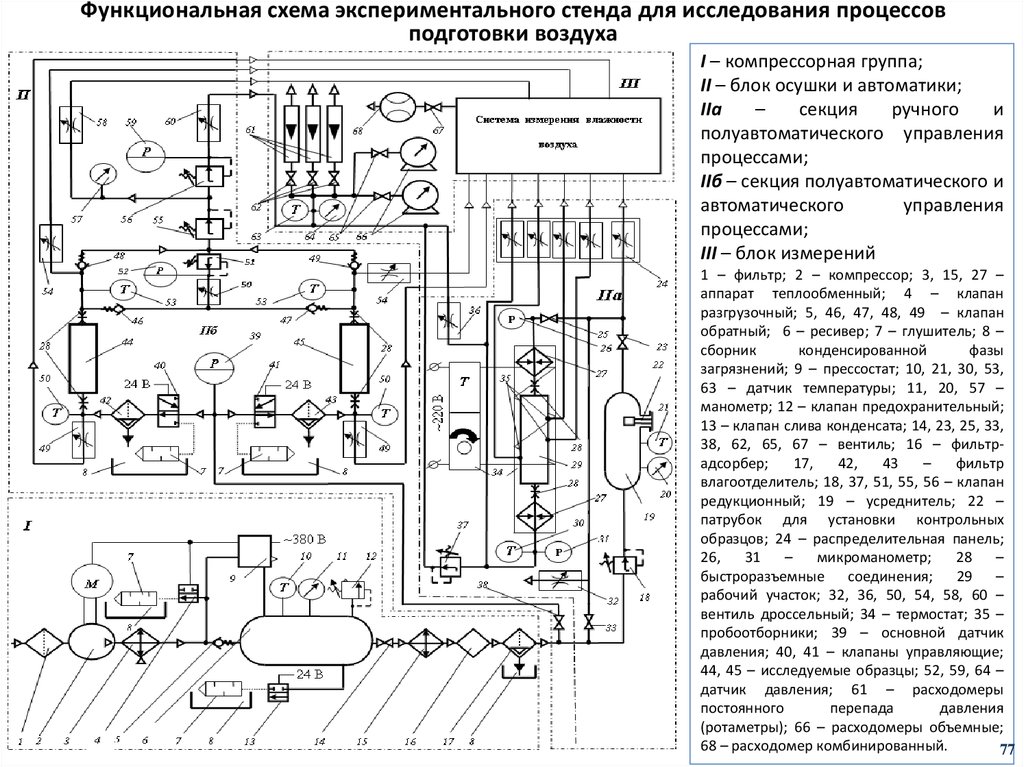





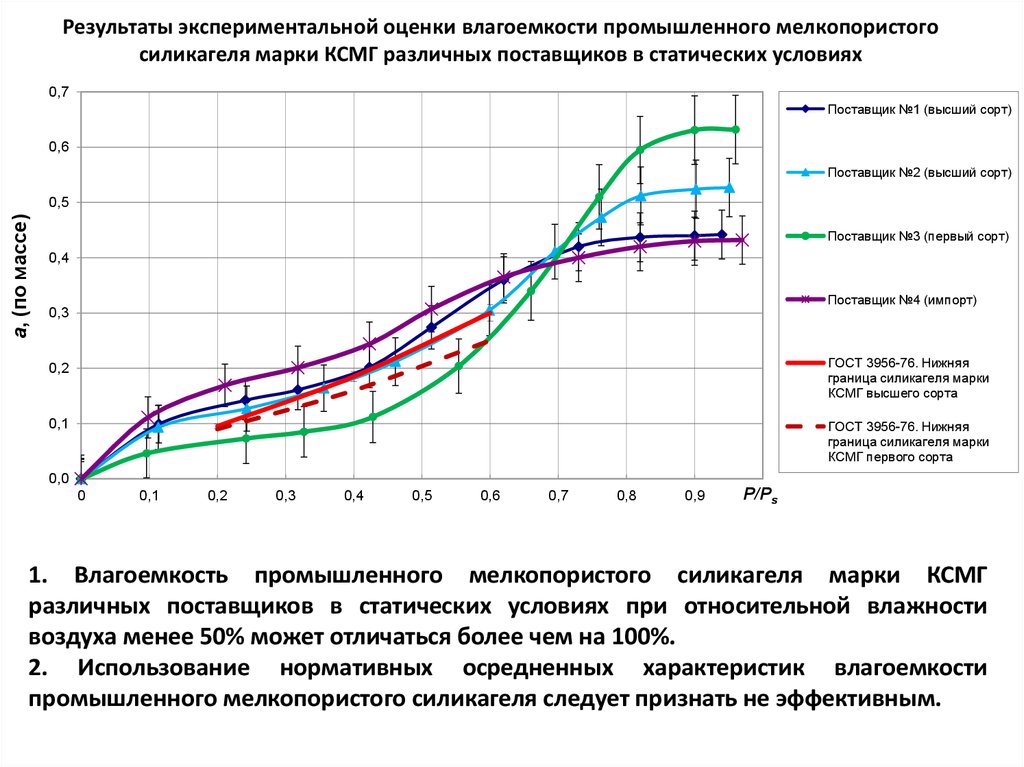
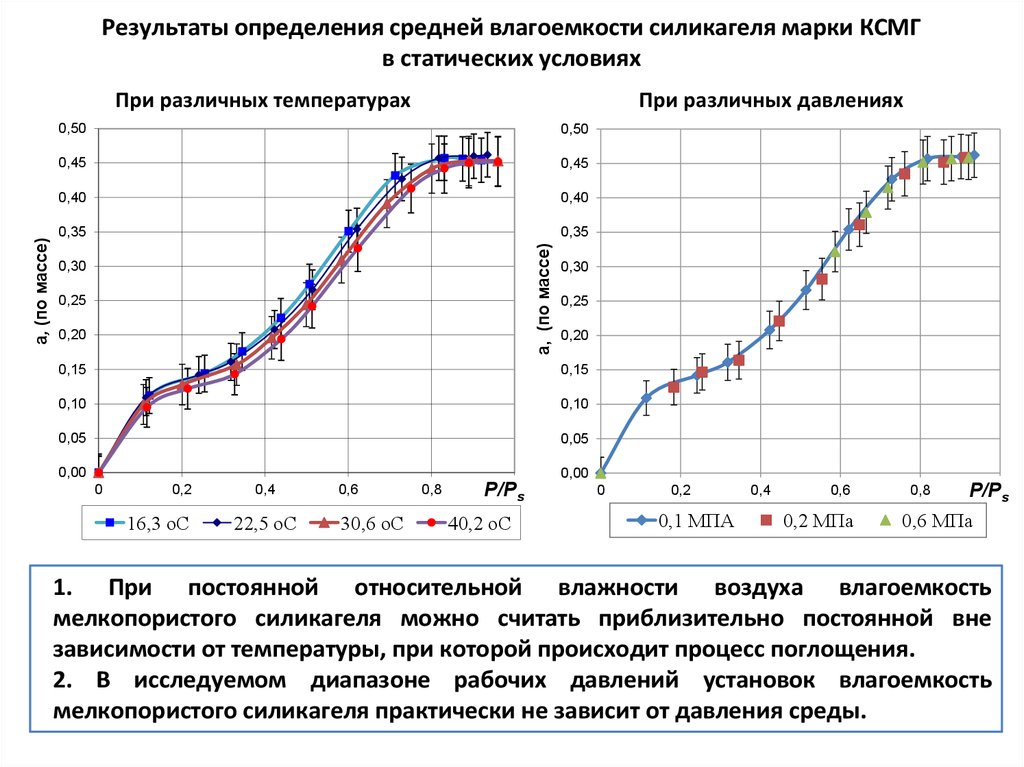
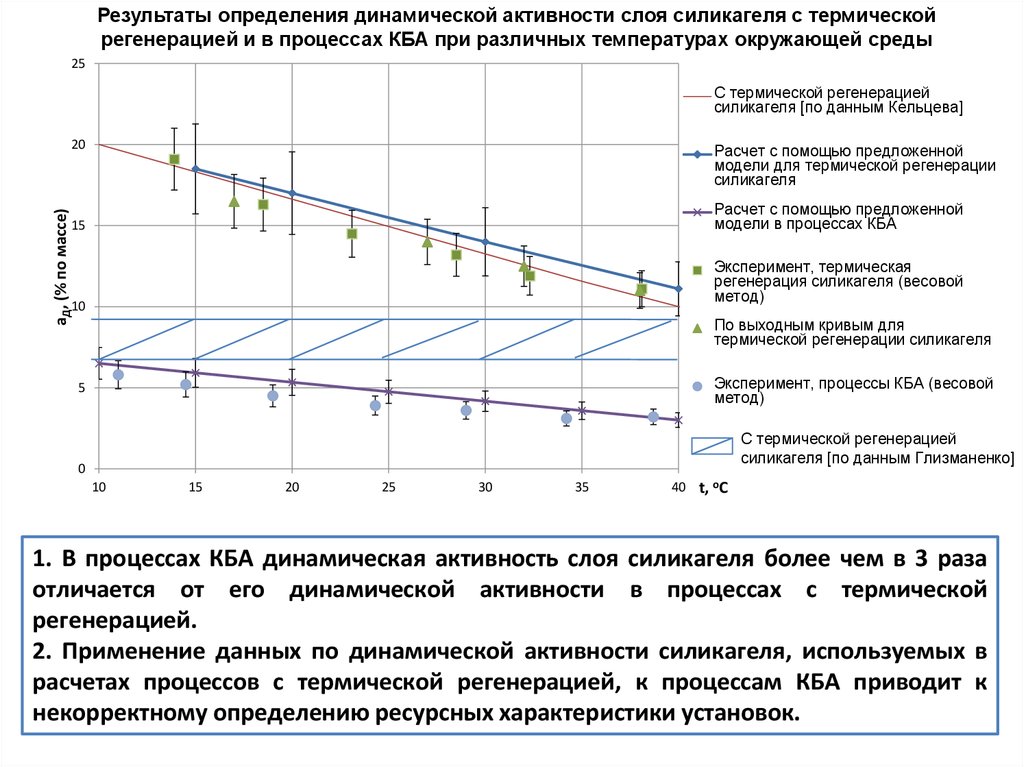
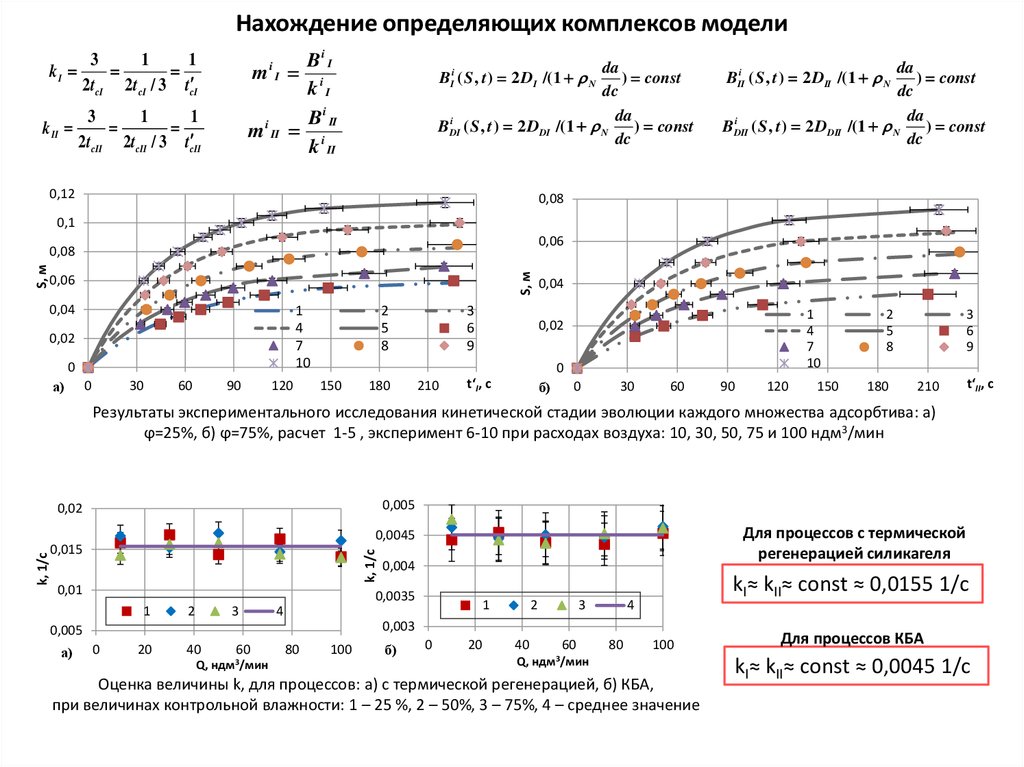
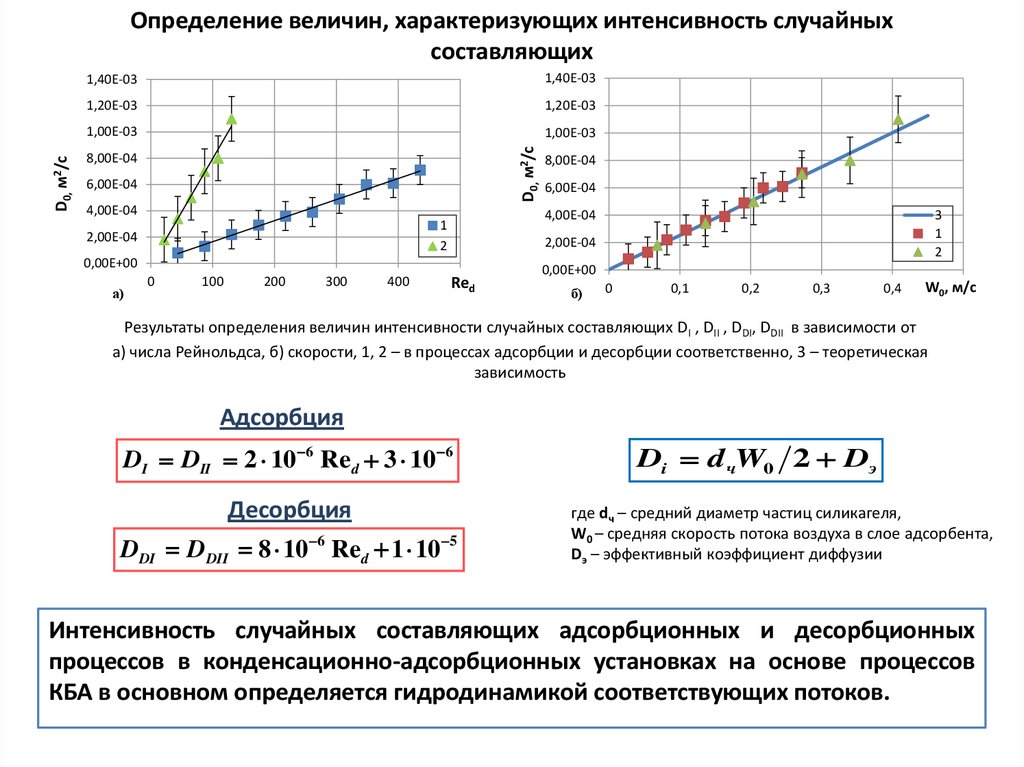
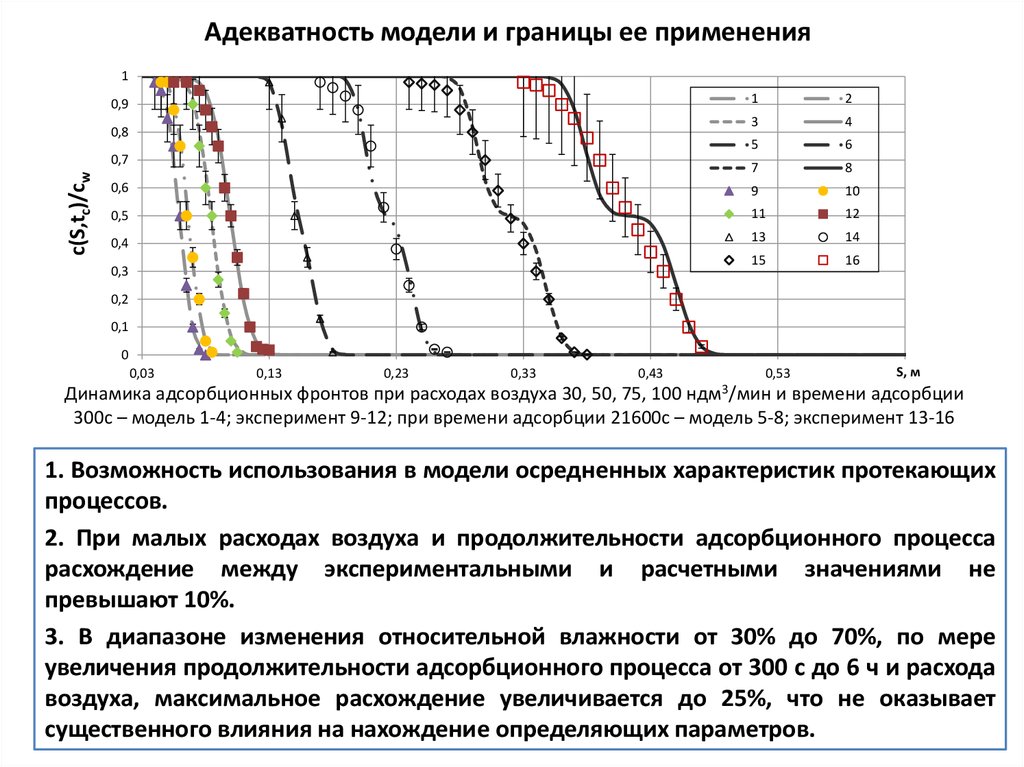
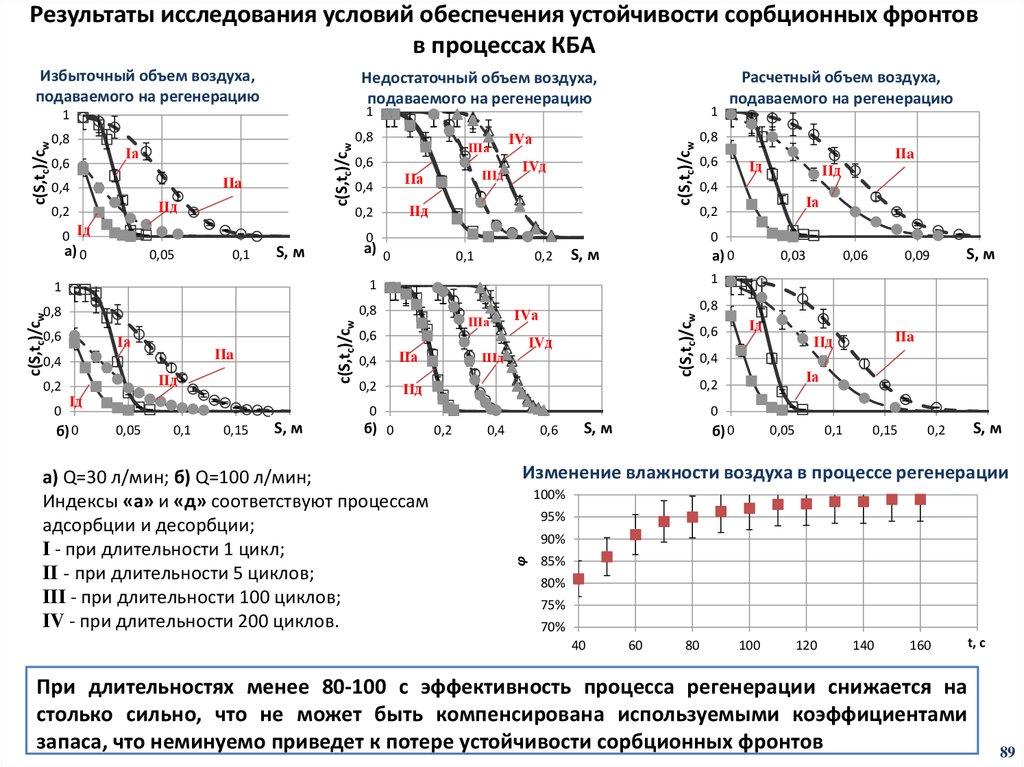
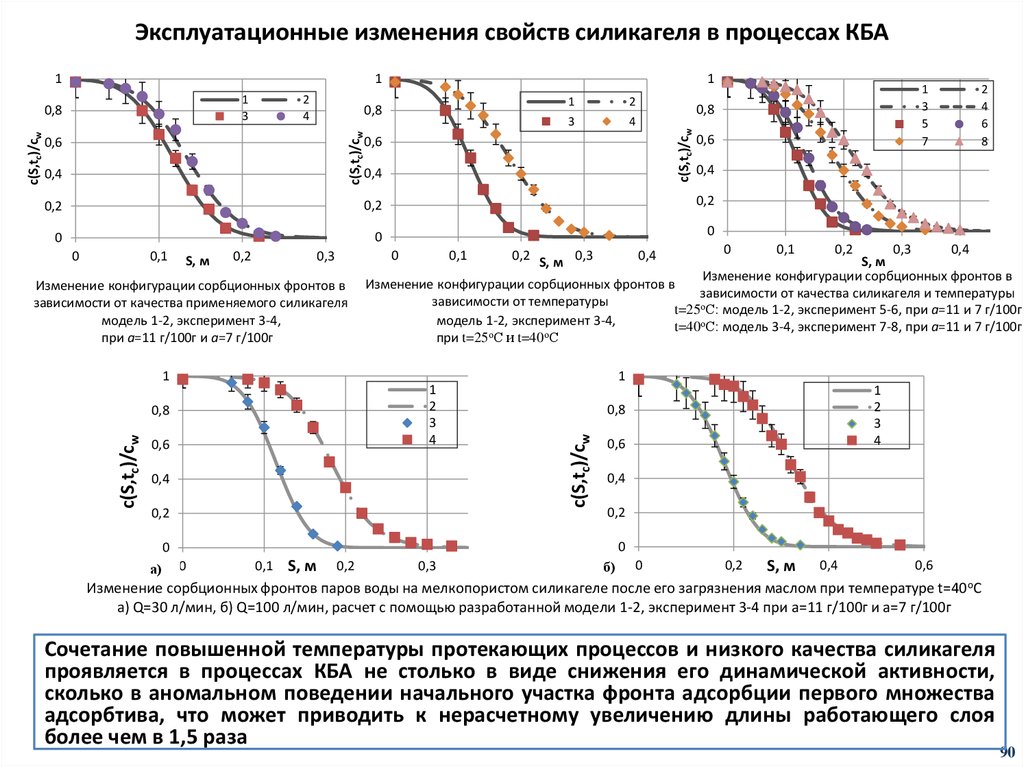

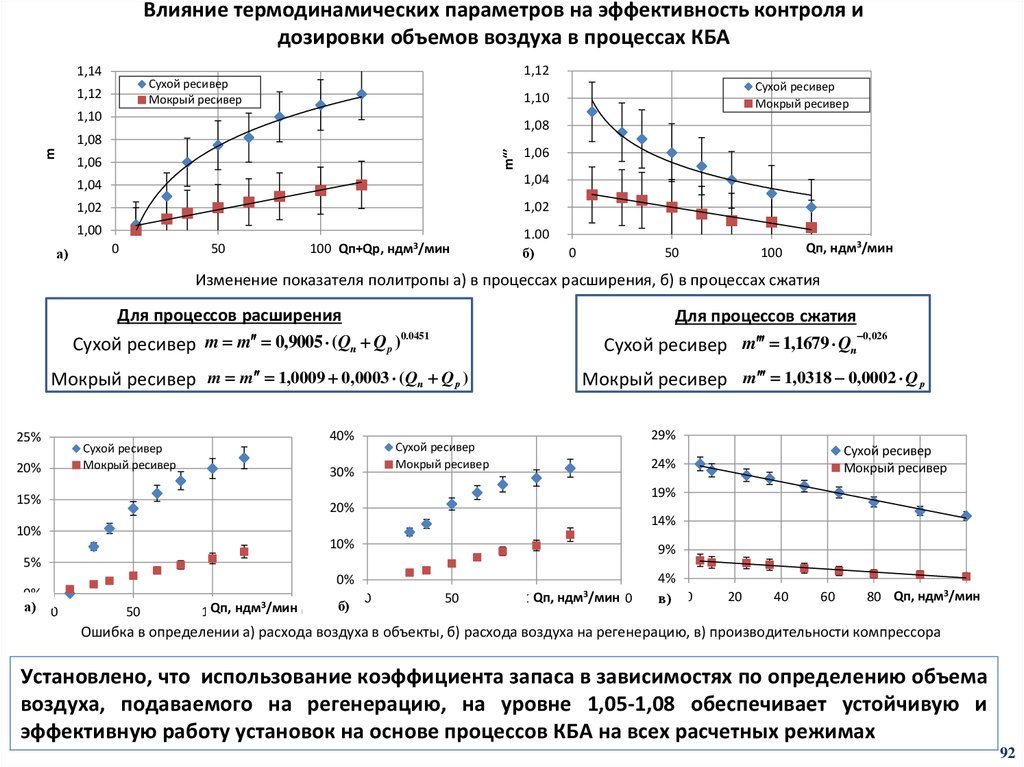
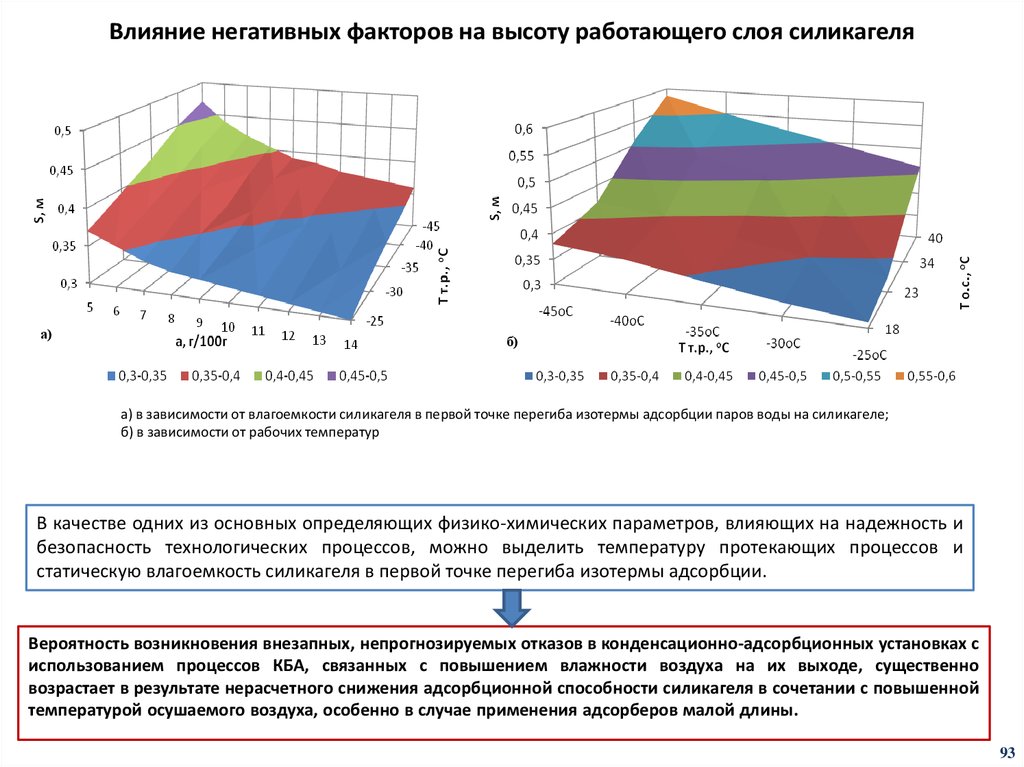
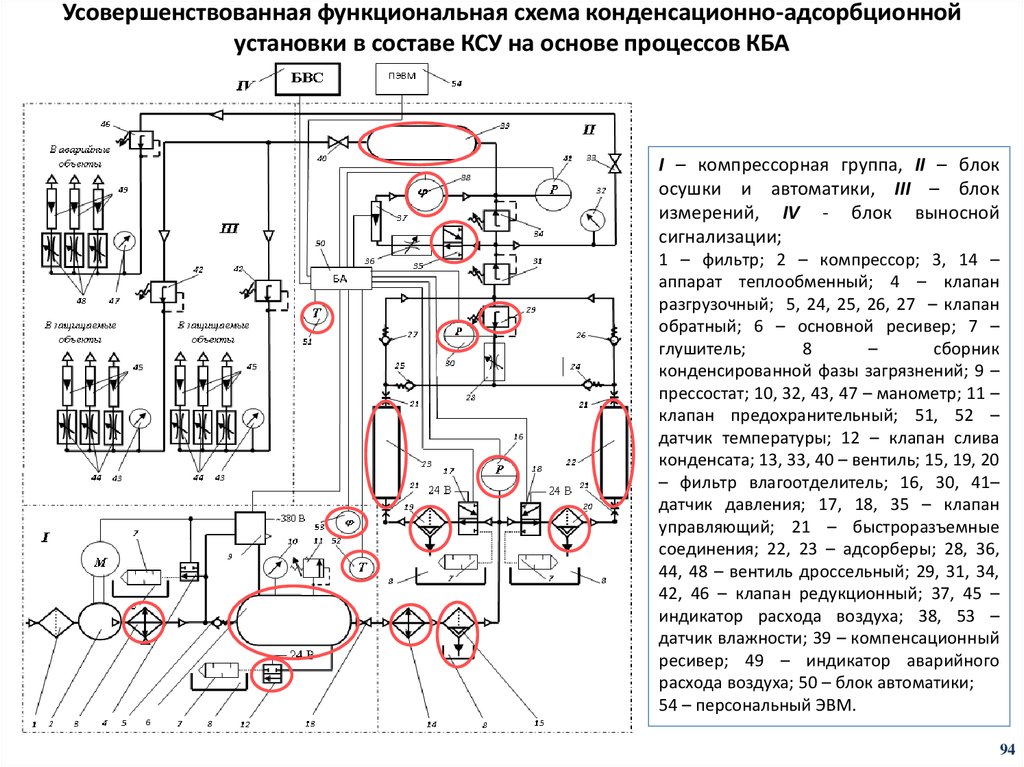
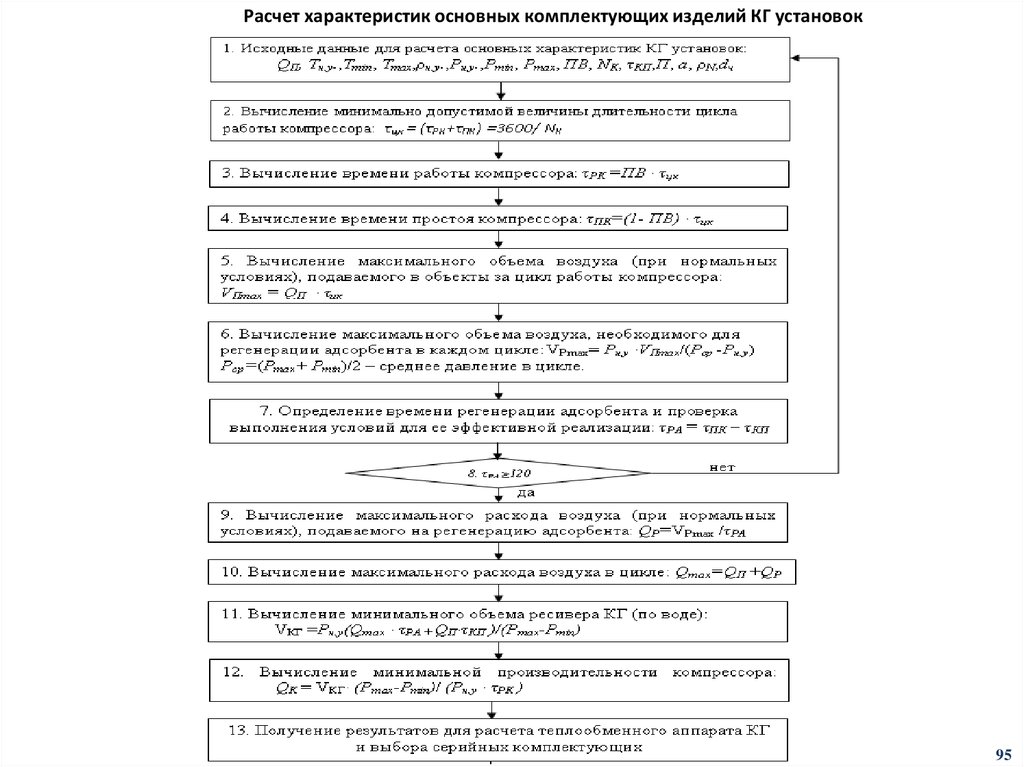
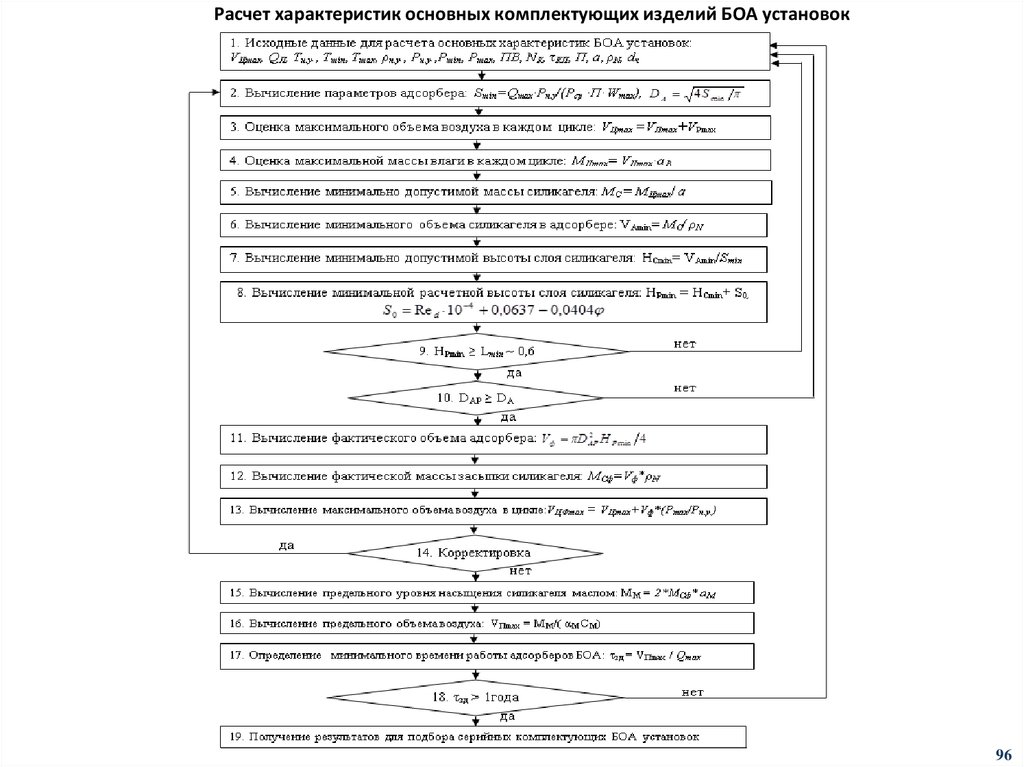









 Физика
Физика








