Похожие презентации:
Способы представления числовых данных в компьютере
1. Задача 1. Задание
Существуют различные способы представления числовых данных вкомпьютере:
несколько форматов целых (со знаком и без),
несколько форматов дробных (с плавающей запятой),
двоично-десятичное представление, и др.
Требуется выбрать формат представления данных для программирования
(при условии экономии памяти для хранения данных):
А) вычислений без погрешностей,
Б) операций считывания и обработки информации с датчиков управляемого
объекта,
В) решения системы уравнений с малой погрешностью (не меньше 10-7),
Г) сбор статистических данных о численности людей разных возрастных
категорий в городе.
Какие типы данных вы выберете для вычислений в случаях А, Б, В, Г?
Поясните свой выбор.
2. Задача 1. Решение
А) вычислений без погрешностейРассмотрим достоинства и недостатки
каждого из способов представления данных
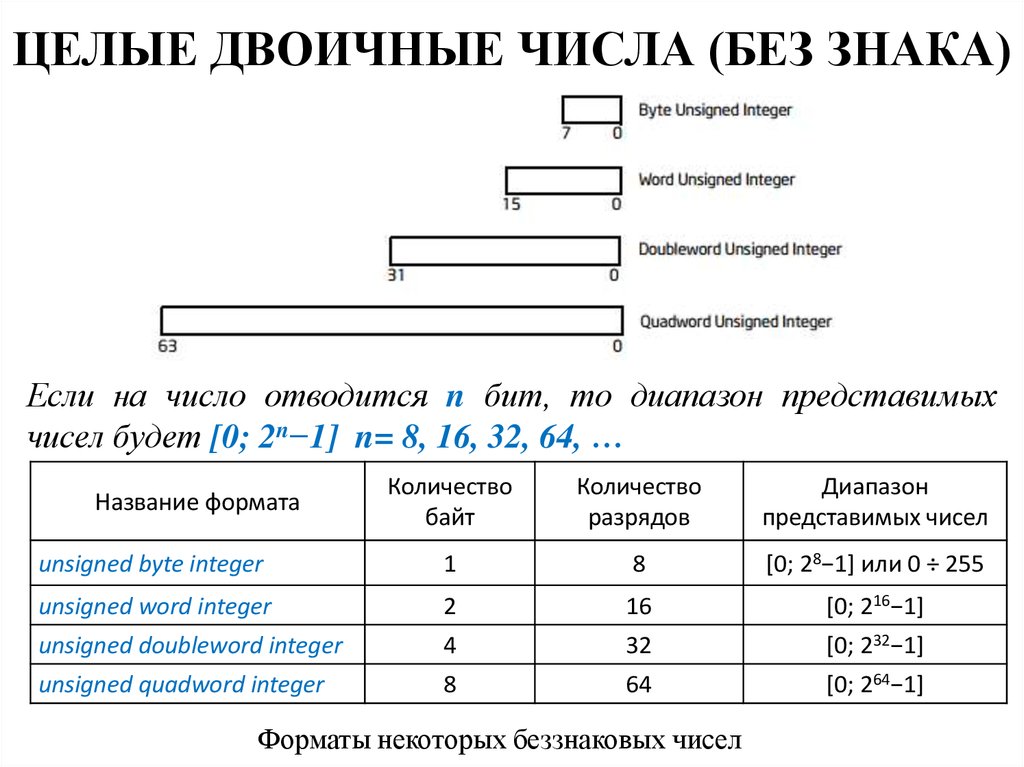
3. ЦЕЛЫЕ ДВОИЧНЫЕ ЧИСЛА (БЕЗ ЗНАКА)
Если на число отводится n бит, то диапазон представимыхчисел будет [0; 2n−1] n= 8, 16, 32, 64, …
Количество
байт
Количество
разрядов
Диапазон
представимых чисел
unsigned byte integer
1
8
[0; 28−1] или 0 ÷ 255
unsigned word integer
2
16
[0; 216−1]
unsigned doubleword integer
4
32
[0; 232−1]
unsigned quadword integer
8
64
[0; 264−1]
Название формата
Форматы некоторых беззнаковых чисел
4. ЦЕЛЫЕ ДВОИЧНЫЕ ЧИСЛА
Основная сложность работы с целыми числами – возможноепереполнение разрядной сетки.
Например (беззнаковые числа):
А = 25510 = 1111 11112= FF16.
В = 25510 = 1111 11112= FF16.
Но после операции сложения
MOV AL,255
ADD AL,255
имеем неверный результат:
Должны получить:
А+В=1FE (510)
5. Задача 1. Решение
А) вычислений без погрешностейА.1. Целое без знака не подходит, т.к.
• при вычислениях могут возникнуть и отрицательные
числа,
• нельзя произвести вычисления с дробными числами,
• ограничен диапазон представимых значений при
максимальной разрядности в 8 байт (в 64-разрядных ВС)
составляет 0÷264
• основная ошибка (погрешность) переполнение разрядной
сетки при получении результата, превышающего диапазон
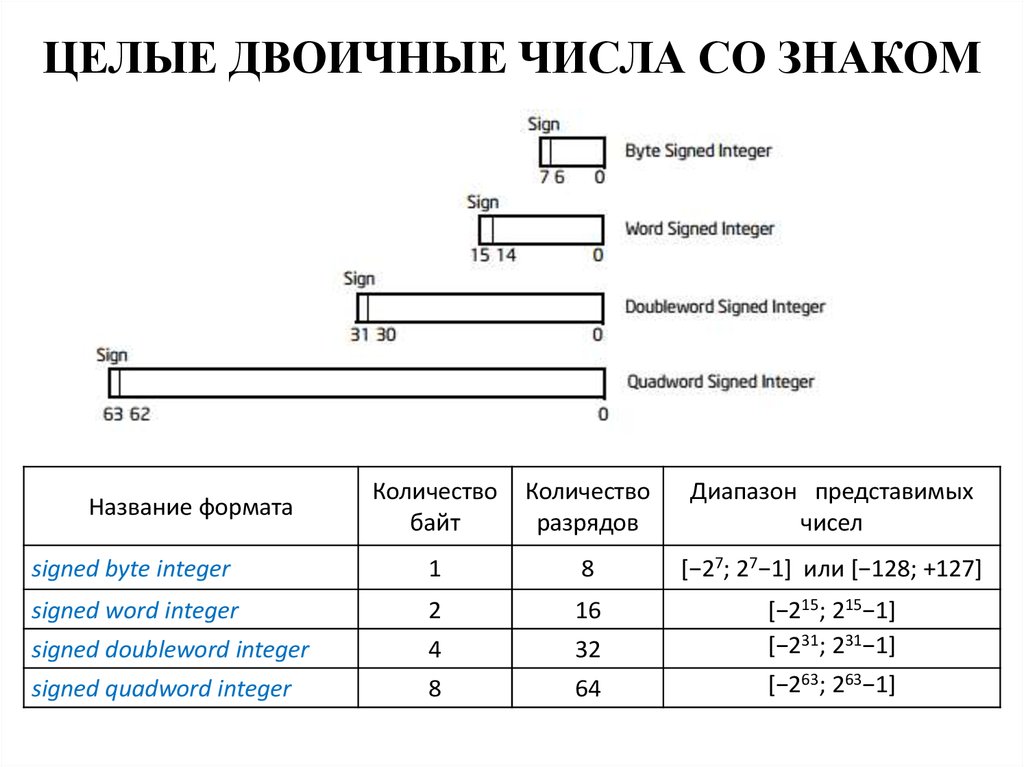
6. ЦЕЛЫЕ ДВОИЧНЫЕ ЧИСЛА СО ЗНАКОМ
Количествобайт
Количество
разрядов
Диапазон представимых
чисел
signed byte integer
1
8
[−27; 27−1] или [−128; +127]
signed word integer
2
16
signed doubleword integer
4
32
[−215; 215−1]
[−231; 231−1]
signed quadword integer
8
64
[−263; 263−1]
Название формата
7. ЦЕЛЫЕ ДВОИЧНЫЕ ЧИСЛА
Основная сложность работы с целыми числами – возможноепереполнение разрядной сетки.
Например (знаковые числа):
А = – 12810 = 1000 00002= 8016.
В = –810 = 1111 10002= F816.
Но после операции сложения
MOV AL, –128
ADD AL, –8
имеем неверный результат:
Должны получить:
А+В=17816 (–13610)
8. Задача 1. Решение
А) вычислений без погрешностейА.2. Целое со знаком не подходит, т.к.
• нельзя произвести вычисления с дробными числами,
• ограничен диапазон представимых значений при
максимальной разрядности в 8 байт (в 64-разрядных ВС)
составляет –263÷+263
• основная ошибка (погрешность) переполнение разрядной
сетки при получении результата, превышающего диапазон
9. ДРОБНЫЕ ЧИСЛА В ФОРМАТЕ С ПЛАВАЮЩЕЙ ЗАПЯТОЙ (ЧПЗ) или FLOAT
Число = ± Мантисса × 2 ±порядокКаждая ячейка памяти с числом соответствующего типа в бинарном виде
содержит (последовательно):
• 1 бит знака (s),
• p бит, выделяемых на хранение порядка числа,
• m бит для хранения мантиссы.
знак
1 бит
порядок
мантисса
p бит
m бит
10. СТАНДАРТЫ ПРЕДСТАВЛЕНИЯ ЧПЗ В КОМПЬЮТЕРЕ
IEEE 754-2008 http://ali.ayad.free.fr/IEEE_2008.pdfТип данных
Размер
(байт)
Точность
s
знак
Разрядность (бит)
р
m
порядок
мантисса
всего
binary16
2
половинная
1
5
10
16
binary32 (float)
4
одинарная
1
8
23
32
binary64 (double)
8
двойная
1
11
52
64
Не стандартизованный
формат Intel
10
расширенная
1
15
64
80
binary128 (long double)
16
учетверённая
1
15
112
128
11. Диапазоны представления чисел с плавающей запятой
ДИАПАЗОНЫ ПРЕДСТАВЛЕНИЯЧИСЕЛ С ПЛАВАЮЩЕЙ ЗАПЯТОЙ
Числа с плавающей запятой одинарной точности могут хранить значение в диапазоне
[–3,37∙1038; –1,17∙10–38] U [1,17∙10–38; 3,37∙1038],
где
минимальное
максимальное
минимальное
максимальное
вещественное
вещественное
вещественное
вещественное
отрицательное число
отрицательное число
положительное число
положительное число
Для чисел с половинной точностью: [–65504; –5.96∙10−8] U [5.96∙10−8; 65504].
Для чисел с двойной точностью: [–1,8∙10308; –2,2∙10–308] U [2,2∙10–308; 1,8∙10308].
Для чисел с расшир. точностью: [–1,18∙104932; – 3,37∙10-4932] U [3.37·10–4932; 1,18 ∙104932].
…
12. ТОЧНОСТЬ ПРЕДСТАВЛЕНИЯ ЧИСЕЛ В КОМПЬЮТЕРЕ
Все целые числа представлены без погрешности.Для действительных чисел:
• вычислительная погрешность
• необходимость перевода дробей из десятичной системы
счисления в двоичную.
⅕=0,2.
Двоичное представление:
4 разрядами после запятой - 0.00112, что соответствует десятичному числу
0.187510
8 разрядами - 0.001100112, что соответствует десятичному числу 0.1992187510
12 разрядами - 0.0011001100112, что соответствует десятичному числу
0.19995117187510
28 разрядами - 0.00110011001100110011001100112, что соответствует
0.1999999992549410
Отсюда видим, что точность представления повышается с увеличением
разрядной сетки. Кроме того, в формате ЧПЗ не могут быть представлены
как очень большие числа, так и очень маленькие.
13. Задача 1. Решение
А) вычислений без погрешностейА.3. Формат с плавающей запятой (точкой) не подходит, т.к.
• хотя диапазон представимых значений достаточно
большой, но все дробные числа за редким исключением
представляются с погрешностью и для точных расчетов
не подходят
14. ДВОИЧНО-ДЕСЯТИЧНЫЕ ДАННЫЕ
Позволяют оперировать любыми типами и размерами чисел безпогрешности (т.к. это формат представления не целого числа, а
лишь одного десятичного разряда).
Необходимое количество десятичных разрядов определяет
пользователь при написании кода программы, т.е. он сам
выбирает точность представления.
;-----------------------------------------------.data
A DB 07H, 09h, 04H
;неупакованное BCD-число 497
B DB 16H, 05H
;упакованное BCD-число 516
;------------------------------------------------
15. ДВОИЧНО-ДЕСЯТИЧНЫЕ ДАННЫЕ
Неупакованное BCD-число.16. ДВОИЧНО-ДЕСЯТИЧНЫЕ ДАННЫЕ
Упакованное BCD-число.старшая тетрада младшая тетрада
№ разряда
7
6
5
4
3
2
1
0
Значение разряда
0
1
0
1
1
0
0
1 Цифры 9 и 5
Вес разрядов
8
4
2
1
8
4
2
1
17. Задача 1. Решение
А) вычислений без погрешностейА.4. Формат
подходит
BCD
двоично-десятичное
представление
• вычисление без погрешностей – ДА
• возможность задания любого размера числа – ДА
• возможность самостоятельно программно определить
знак числа и положение запятой – ДА
• из двух форматов больше подходит упакованный, т.к. он
позволяет в два раза сократить занимаемую числом
область памяти
18. Задача 1. Решение
А) вычислений без погрешностейРешение: Формат BCD двоично-десятичного представления
19. Задача 1. Решение
Б) операций считывания и обработки информации с датчиковуправляемого объекта
Решение
Сложный формат ЧПЗ, вектора, BCD не нужен
Приемлем формат целого двоичного числа без знака, т.к. информация с
датчиков представляет собой набор кодов сигналов – двоичных цифр,
знак не требуется, дробная часть не нужна, самый экономный размер
двоичного числа – byte unsigned integer (1 байт без знака).
20. Задача 1. Решение
В) решения системы уравнений с малой погрешностью (не больше 10-7)Решение
Из-за возможных дробных решений можно сравнить три формата
• ЧПЗ (float),
• BCD,
• Вектора (sse/avx),
Сложно программируемый формат BCD не нужен, т.к. оговорена возможность наличия
погрешности.
Приемлем формат данных ЧПЗ (float) и векторных ЧПЗ. Среди размерности чисел следует
выбрать (при условии экономии памяти) наименьший формат, дающий допустимую
погрешность.
точность представления числа (количество верных десятичных знаков после
запятой) :
Binary32: log10 (мантиссы) = log10 (223)=6,92 ≈ 7
Binary64: log10 (252)=15,65 ≈ 16
Binary128: log10 (2112)=33,7 ≈ 34
…
более высокой точности не требуется.
21. Задача 1. Решение
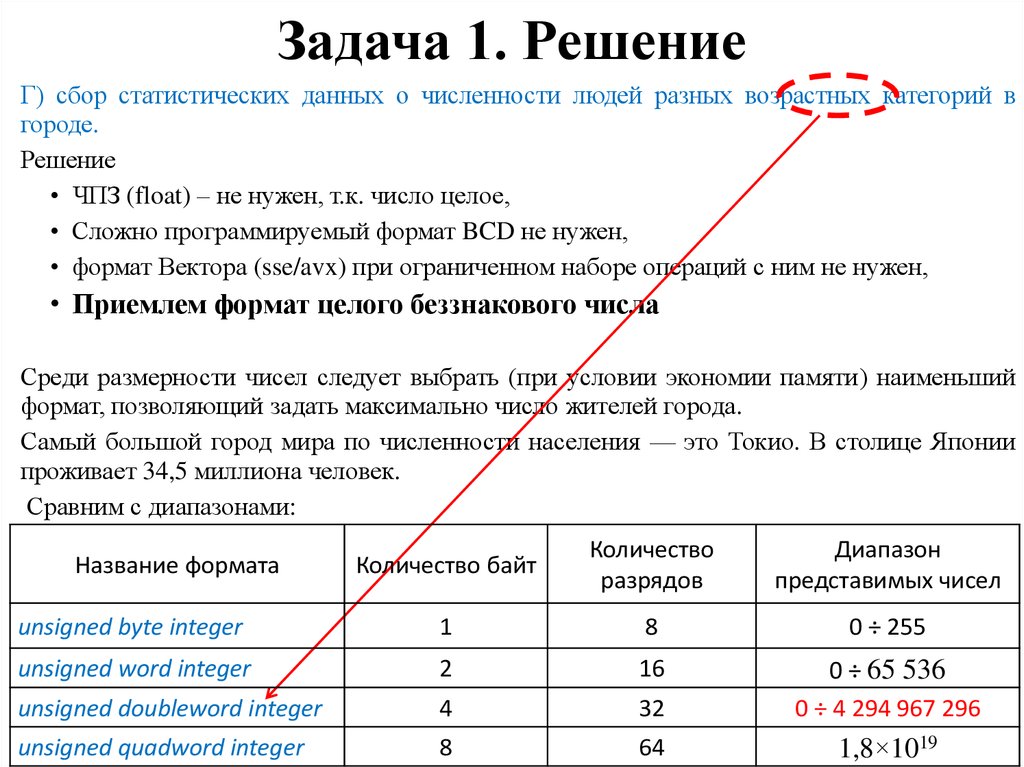
Г) сбор статистических данных о численности людей разных возрастных категорий вгороде.
Решение
• ЧПЗ (float) – не нужен, т.к. число целое,
• Сложно программируемый формат BCD не нужен,
• формат Вектора (sse/avx) при ограниченном наборе операций с ним не нужен,
• Приемлем формат целого беззнакового числа
Среди размерности чисел следует выбрать (при условии экономии памяти) наименьший
формат, позволяющий задать максимально число жителей города.
Самый большой город мира по численности населения — это Токио. В столице Японии
проживает 34,5 миллиона человек.
Сравним с диапазонами:
Количество байт
Количество
разрядов
Диапазон
представимых чисел
unsigned byte integer
1
8
0 ÷ 255
unsigned word integer
2
16
unsigned doubleword integer
4
32
0 ÷ 65 536
0 ÷ 4 294 967 296
unsigned quadword integer
8
64
1,8×1019
Название формата
22. Задача 2. Задание
Установитепоследовательность
в
порядке
возрастания следующих дробных чисел в формате ЧПЗ
одинарной точности, расположенные по адресам (см.
рис. ниже):
А1 по адресу 00402000,
А2 по адресу 00402004,
А3 по адресу 00402014.
23. Задача 2. Задание
Установитепоследовательность
в
порядке
возрастания следующих дробных чисел в формате ЧПЗ
одинарной точности, расположенные по адресам (см.
рис. ниже):
А1 по адресу 00402000,
А2 по адресу 00402004,
А3 по адресу 00402014.
по адресу 00402000 расположены 4 байта кода числа А1 – 00 00 00 00,
по адресу 00402004 расположены 4 байта кода числа А2 – 5F 70 09 B0,
по адресу 00402014 расположены 4 байта кода числа А3– 05 FC FD 02
24. Побайтное хранение кодов
Размер стандартных машинных элементов данных кратен степенямдвойки:
• 1 байт
20 байт = 8 бит
• 2 байта – слово
21 байт = 16 бит
• 4 байта – двойное слово
22 байт = 32 бит
• 8 байт – учетверённое слово
23 байт = 64 бит
•…
00
F0
0F
FF
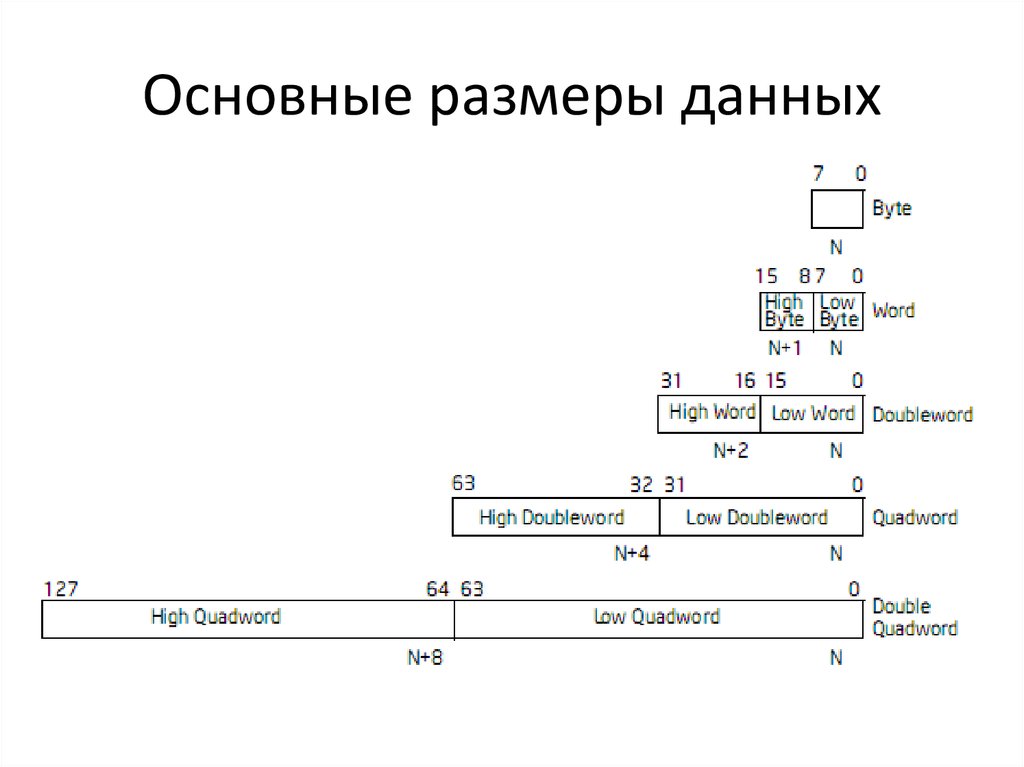
25. Основные размеры данных
26.
СПОСОБЫ ХРАНЕНИЯ МНОГОБАЙТОВЫХЭЛЕМЕНТОВ ДАННЫХ В ПАМЯТИ КОМПЬЮТЕРА
адрес
байта
в ОП
k
k+1
k+2
k+3
ОП
ОП
байт № 3 – 0000 0000
байт № 0 – 1111 1111
байт № 2 – 1111 0000
байт № 1 – 0000 1111
4-байтовое
число
15 732 73510
байт № 1 – 0000 1111
байт № 2 – 1111 0000
адрес
байта в
ОП
k
k+1
k+2
k+3
байт № 0 – 1111 1111
байт № 3 – 0000 0000
big-endian
little-endian
Прямой: от старшего к младшему
IBM, Motorola, SPARC
Обратный: от младшего к старшему
Intel
Порядок следования байтов числа в памяти
27.
Задача 2. Решениеархитектура «Little Endian»
правильная привычная нам запись заданных
чисел будет следующая:
А1 = 00 00 00 00,
А2 = B0 09 70 5F,
А3 = 02 FD FC 05.
28. Задача 2. Решение
архитектура «Little Endian»А1 = 00 00 00 00,
А2 = B0 09 70 5F,
А3 = 02 FD FC 05.
Знак числа
для А1 цифра 016 = 00002, число А1 – положительный ноль
для А2 цифра В16= 10112, число А2 – отрицательное
для А3 цифра 016 = 00002, число А3 – положительное и не равно нулю.
Следовательно, верен следующий порядок чисел по возрастанию:
A2, A1, A3
29. Задача 2. Решение
архитектура «Big Endian»А1 = 00 00 00 00,
А2 = 5F 70 09 B0,
А3 = 05 FC FD 02.
Знак числа
для А1 цифра 016 = 00002, число А1 – положительный ноль
для А2 цифра 516= 01012, число А2 – положительное и не равно нулю
для А3 цифра 016 = 00002, число А3 – положительное и не равно нулю.
Следовательно, для сравнения А2 и А3 надо установить содержимое других полей числа
(порядок, мантисса). Больше то, где больше порядок, и если порядки равны, сравнить мантиссы.
А2: 01011111 0111000 0001001 1011000
А3: 00000101 11111100 11111101 00000010
Порядок А2 > порядка А3.
Следовательно верен следующий порядок чисел по возрастанию:
A1, A3, A2

























 Информатика
Информатика