Похожие презентации:
Множества. Операции над множествами
1.
Множества.Операции над
множествами
1
23
0011 0010 1010 1101 0001 0100 1011
45
1
2
4
2.
0011 0010 1010 1101 0001 0100 1011МНОЖЕСТВО
ЭЛЕМЕНТ МНОЖЕСТВА
ВИДЫ МНОЖЕСТВ
ОТНОШЕНИЯ МЕЖДУ
МНОЖЕСТВАМИ
ОБЪЕДИНЕНИЕ МНОЖЕСТВ
ПЕРЕСЕЧЕНИЕ МНОЖЕСТВ
НАХОДИТЬ
ОБЪЕДИНЕНИЕ
МНОЖЕСТВ
1
НАХОДИТЬ
ПЕРЕСЕЧЕНИЕ
МНОЖЕСТВ
2
4
ИЗОБРАЖАТЬ С
ПОМОЩЬЮ КРУГОВ
ЭЙЛЕРА
РЕШАТЬ ЗАДАЧИ С
ИСПОЛЬЗОВАНИЕМ
ИМЕЮЩИХСЯ ЗНАНИЙ
3.
«Множество есть многое,мыслимое нами как
единое»
0011 0010 1010 1101 0001 0100 1011
основатель теории множеств
Георг Кантор
1
2
4
4. Понятия теории множеств
0011 0010 1010 1101 0001 0100 1011Понятие множества является одним из
наиболее общих и наиболее важных
математических понятий. Оно было введено
в математику немецким ученым Георгом
Кантором (1845-1918).Следуя Кантору,
понятие "множество" можно определить так:
1
2
4
Множество- совокупность объектов,
обладающих определенным свойством,
объединенных в единое целое.
5. Придумай название для предметов и животных, собранных вместе:
0011 0010 1010 1101 0001 0100 1011НАБОР
КОЛЛЕКЦИЯ МАРОК КАРАНДАШЕЙ
ЧАЙНЫЙ СЕРВИЗ
БУКЕТ ЦВЕТОВ
1
СТАЯ ПТИЦ
2
4
СТАДО КОРОВ
6.
Множество – совокупность объектов,объединенных по какому–нибудь признаку.
0011 0010 1010 1101 0001 0100 1011
Множества обозначают большими буквами
латинского алфавита: А, В, С, D и т. д.
Объекты, составляющие множество,
называются элементами множества.
1
2
4
7.
множествоМножество
0011 0010
1010 1101 0001 0100 1011
четырехугольников
Пространственные тела
Натуральные числа
элемент
Трапеция, параллелограмм, ромб,
квадрат, прямоугольник
Шар, прямоугольный
параллелепипед, призма,
пирамида, октаэдр
1
2
1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11…
4
Квадраты чисел
1, 4, 9, 16, 25, 36, 49, 64, 81, 100 ..
Цифры десятичной системы
счисления
0, 1, 2, 3, 4, 5, 6, 7, 8, 9
Двузначные четные числа
10, 12, 14, 16 … 96, 98
8.
множество людей на Солнце0011 0010 1010 1101 0001 0100 1011
множество прямых углов равностороннего
треугольника
множество точек пересечения двух
параллельных прямых
1
2
4
Пустое множество- множество, не
содержащее ни одного элемента.
9.
0011 0010 1010 1101 0001 0100 1011Z
Q
R
N
1
2
4
10.
Обозначения некоторыхчисловых множеств:
0011 0010 1010 1101 0001 0100 1011
N – множество натуральных чисел;
Z – множество целых чисел;
Q – множество рациональных чисел;
I - множество иррациональных чисел;
R – множество действительных чисел.
1
2
4
11. Стандартные обозначения
0011 0010 1010 1101 0001 0100 10111
2
4
12. ВИДЫ МНОЖЕСТВ
Запишите множества букв словКОНИ И КИНО
0011 0010 1010 1101 0001 0100 1011
{К, О, Н, И}
{К, И, Н, О}
Равные множества
1
2
4
13. ВИДЫ МНОЖЕСТВ
0011 0010 1010 1101 0001 0100 1011А = {2; 3; 5; 7; 11; 13};
{х | 5< х <12}
Конечные множества
1
2
4
14. ВИДЫ МНОЖЕСТВ
0011 0010 1010 1101 0001 0100 1011{1; 4; 9; 16; 25; …};
{10; 20; 30; 40; 50; …};
Бесконечные множества
1
2
4
15.
Среди перечисленных ниже множеств укажите0011 0010конечные
1010 1101 0001
1011
и 0100
бесконечные
множества:
а) множество чисел, кратных 13;
б) множество делителей числа 15;
в) множество деревьев в лесу;
г) множество натуральных чисел;
д) множество рек Ростовской области;
е) множество корней уравнения х + 3 = 11;
ж) множество решений неравенства х + 1 < 3.
1
2
4
16.
Задайте множество цифр, с помощью которыхзаписывается число:
0011 0010
1010 1101
0001в)
0100
1011 г) 555555.
а) 3254;
б) 8797;
11000;
Охарактеризуйте множество А:
а) А = {1, 3, 5, 7, 9};
б) А = {- 2, - 1, 0, 1, 2};
в) А = {11, 22, 33, 44, 55, 66, 77, 88, 99};
1
2
4
17.
Даны множества:М = {5, 4, 6},
0011 0010 1010 1101 0001 0100 1011
Р = {4, 5, 6},
Т = {5, 6, 7},
S = {4, 6}.
Р
М
S
Какое из утверждений неверно?
а) М = Р
б) Р ≠ S
в) М ≠ Т
г) Р = Т
1
2
4
T
18. Отношения между множествами
0011 0010 1010 1101 0001 0100 10111
2
4
19.
0011 0010 1010 1101 0001 0100 10111
2
4
20.
0011 0010 1010 1101 0001 0100 10111
2
4
21.
0011 0010 1010 1101 0001 0100 1011Пусть А — множество простых чисел вида
7n + 2, где n ∈ N.
Верна ли запись -5 ∈ А.
1
2
4
22.
0011 0010 1010 1101 0001 0100 1011Задайте перечислением элементов множество,
заданное характеристическим свойством
A x | x N , x2 2x 0
1
2
4
23.
1. В множестве {лев; лисица; гиена; слон; рысь} всеэлементы, кроме одного, обладают некоторым
0011свойством.
0010 1010 1101 0001 0100 1011
а) опишите это свойство;
б) найдите элемент, не обладающий этим свойством;
в) назовите еще два элемента, обладающие этим
свойством.
1
2
2. Назовите 5 подмножеств в множестве всех цветов
радуги.
4
3. Каким свойством в множестве ромбов выделяется
подмножество квадратов?
24.
множеств А и В называется0011множество,
0010 1010 1101 0001
0100 1011
содержащее
все элементы,
которые принадлежат множеству А или В.
П р и м е р : {1,2,3}
1
Объединение множеств обозначается
2
{2,3,4} = {1,2,3,4}.
4
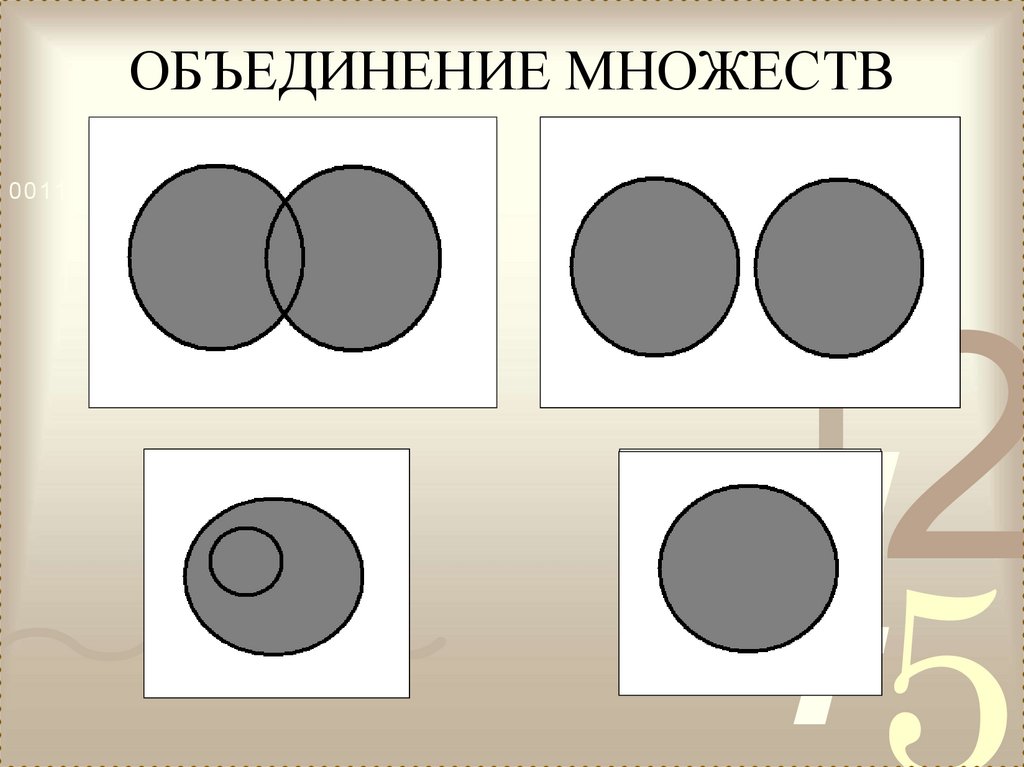
25. ОБЪЕДИНЕНИЕ МНОЖЕСТВ
0011 0010 1010 1101 0001 0100 10111
2
4
26. А – четные натуральные числа В – двузначные числа
0011 0010 1010 1101 0001 0100 1011Найти объединение этих множеств.
А
В – быть четным натуральным или
двузначным числом
Пример: 8 и 32
1
2
4
27.
множеств А и В называется0011множество,
0010 1010 1101 0001
0100 1011
содержащее
все элементы,
которые принадлежат множествам А и В
одновременно.
Пересечение множеств обозначается
Пример:
{1,2,3}
1
2
4
{2,3,4} = {2,3}
28. БЛИЦ-ОПРОС
0011 0010 1010 1101 0001 0100 1011БЛИЦ-ОПРОС
1
2
4
29. БЛИЦ-ОПРОС
Какие0011 0010 1010 1101 0001 0100 1011
названия
• земноводные,
применяются
млекопитающие,
для
хладнокровные и
обозначения
т.п.
множеств
животных?
1
2
4
30. БЛИЦ-ОПРОС
Какие0011 0010
1010 1101 0001 0100 1011
названия
применяются • рота, взвод, полк,
для
дивизия и т.п.
обозначения
множеств
военнослужащих?
1
2
4
31. БЛИЦ-ОПРОС
Как0011 0010 1010 1101 0001 0100 1011
называется
множество
цветов,
• букет
стоящих в
вазе?
1
2
4
32. БЛИЦ-ОПРОС
Как называется0011 0010 1010 1101 0001 0100 1011
множество
точек земной
поверхности,
• экватор
равноудаленных
от обоих
полюсов?
1
2
4
33. БЛИЦ-ОПРОС
0011 0010 1010 1101 0001 0100 1011Как называется
множество
населённых
людьми мест?
• деревня, село,
город, посёлок
1
2
4
34. БЛИЦ-ОПРОС
0011 0010 1010 1101 0001 0100 1011Как называется
множество
картин?
• выставка,
галерея
1
2
4
35. БЛИЦ-ОПРОС
0011 0010 1010 1101 0001 0100 1011Как называется
множество
документов?
• архив
1
2
4
36. БЛИЦ-ОПРОС
Какие0011 0010 1010 1101 0001 0100 1011
названия
применяют
для
• флотилия,
обозначения
эскадра
множеств
кораблей?
1
2
4
37.
множеств А и В называется0011множество,
0010 1010 1101 0001
0100 1011
содержащее
все элементы,
которые принадлежат множеству А или В.
П р и м е р : {1,2,3}
1
Объединение множеств обозначается
2
{2,3,4} = {1,2,3,4}.
4
38. ОБЪЕДИНЕНИЕ МНОЖЕСТВ
0011 0010 1010 1101 0001 0100 10111
2
4
39. А – четные натуральные числа В – двузначные числа
А – четные натуральные числа0011В
0010
1101 0001 0100 числа
1011
– 1010
двузначные
Найти объединение этих множеств.
1
А
В – быть четным натуральным или
двузначным числом
Пример: 8 и 32
2
4
40.
множеств А и В называется0011множество,
0010 1010 1101 0001
0100 1011
содержащее
все элементы,
которые принадлежат множествам А и В
одновременно.
Пересечение множеств обозначается
Пример:
{1,2,3}
1
2
4
{2,3,4} = {2,3}
41. ПЕРЕСЕЧЕНИЕ МНОЖЕСТВ
0011 0010 1010 1101 0001 0100 10111
2
4
42. А – четные натуральные числа В – двузначные числа
0011 0010 1010 1101 0001 0100 1011Найти пересечение этих множеств.
А
В – быть четным натуральным и
двузначным числом
Пример: 32
1
2
4
43.
Даны множества:0011 0010 1010 1101 0001 0100 1011
А = {2; 3; 8},
В = {2; 3; 8; 11},
С = {5; 11}.
Найдите: 1) АUВ; 2) АUС; 3) СUВ.
1
2
4
44.
Даны множества:0011 0010 1010 1101 0001 0100 1011
А = {a, b, c, d},
B = {c, d, e, f},
C = {c, e, g, k}.
Найдите: (АUВ)UС.
1
2
4
45.
Даны множества:0011
1010 1101 0001всех
0100 1011
А0010
– множество
натуральных чисел,
кратных 10,
В = {1; 2; 3;…, 41}.
Найдите А∩В.
1
2
4
46.
Решение задачис помощью кругов Эйлера
K
0011 0010 1010 1101 0001 0100 1011
k
Леона́рд Э́йлер — швейцарский,
немецкий и российский математик,
внёсший значительный вклад в
развитие математики, а также
механики, физики, астрономии и
ряда прикладных наук.
1
2
4
47.
В классе 30 человек, каждый из которых поётили танцует. Известно, что поют 17 человек, а
танцевать умеют 19 человек. Сколько человек
0011
0010 1010
1101 0001 одновременно?
0100 1011
поёт
и танцует
Всего 30
11
6
поют 17
17+19=36, всего 30
13
1
2
4
танцуют 19
36-30=6
48. Решение
Пусть А - это множество учеников, умеющих петь.Количество
элементов
в нём по условию равно n = 17.
0011
0010 1010 1101
0001 0100 1011
Пусть В - множество учеников, умеющих танцевать.
Количество элементов в нём - m = 18. Множество
совпадает со всем классом, т.к. каждый ученик в
классе поёт или танцует. А В - это множество тех
учеников класса, которые поют и танцуют
одновременно. Пусть их количество равно k.
Согласно формуле доказанной выше
n + m- k = 17+ 19- k = 30 k = 6.
Ответ: 6 учеников в классе поют и танцуют
одновременно.
1
2
4
49.
На фирме работают 67 человек. Из них 47 знаютанглийский язык, 35 - немецкий язык, а 23 - оба
языка. Сколько человек в фирме не знают ни
0011 0010 1010 1101 0001 0100 1011
английского, ни немецкого языков?
Английский 47
Всего 67
Немецкий 35
35-23=12
47-23=24
12
24
23
1
2
4
24+12+23=59
67- 59=8
50. Каждый учащийся в классе изучает английский или французский язык. Английский язык изучают 25 учащихся, французский — 27
0011 0010 1010 1101 0001 0100 1011учащихся, а два языка — 18 учащихся. Сколько
учащихся в классе?
18
Только английский
25 – 18 = 7
1
2
Немецкий 27
Английский 25
7
9
Только немецкий
27 – 18 = 9
4
7 + 9 + 18 = 34
Ответ: в классе 34 ученика
51.
Расположите 4 элемента в двух множествахтак,
чтобы
в каждом
0011 0010
1010
1101 0001
0100 1011 из них было по 3
элемента.
1
2
4
52.
Множества А и В содержат соответственно 5 и 6элементов,
множество
0011 0010
1010 1101а0001
0100 1011А ∩ В – 2 элемента. Сколько
элементов в множестве А U В?
1
2
4
Объединение содержит 9 элементов
53.
Каждая семья, живущая в нашем доме, выписывает илигазету, или журнал, или и то и другое вместе. 75 семей
0011 0010 1010 1101 0001 0100 1011
выписывают газету, а 27 семей выписывают журнал и
лишь 13 семей выписывают и журнал, и газету.
Сколько семей живет в нашем доме?
1
Всего: 14 + 13 + 62 =89
2
4
53
54.
На школьной спартакиаде каждый из 25 учеников 9 –го0011 0010
1010 выполнил
1101 0001 0100
1011
класса
норматив
или по бегу, или по
прыжкам в высоту. Оба норматива выполнили 7
человек, а 11 учеников выполнили норматив по бегу, но
не выполнили норматив по прыжкам в высоту.
Сколько учеников выполнили норматив: а) по бегу; б)
по прыжкам в высоту; в) по прыжкам при условии, что
не выполнен норматив по бегу?
1
2
4
55.
Из 52 школьников 23 собирают значки, 35 собираютмарки,
а 16 0001
– и значки,
и марки. Остальные не
0011 0010
1010 1101
0100 1011
увлекаются коллекционированием. Сколько
школьников не увлекаются коллекционированием?
1
2
4
55
56.
Каждый из учеников 9-го класса в зимние каникулыровно
раза
театре, посмотрев спектакли А, В
0011 0010
1010два
1101
0001был
0100в1011
или С. При этом спектакли А, В, С видели
соответственно 25, 12 и 23 ученика. Сколько учеников
в классе?
1
2
4
57.
В воскресенье 19 учеников нашего класса побывали в0011 0010 1010 1101 0001 0100 1011
планетарии, 10 – в цирке и 6 – на стадионе. Планетарий
и цирк посетили 5 учеников; планетарий и стадион 3; цирк и стадион - 1. Сколько учеников в нашем
классе, если никто не успел посетить все три места, а
три ученика не посетили ни одного места?
1
2
4
58.
0011 0010 1010 1101 0001 0100 1011МНОЖЕСТВО
ЭЛЕМЕНТ МНОЖЕСТВА
ВИДЫ МНОЖЕСТВ
ОТНОШЕНИЯ МЕЖДУ
МНОЖЕСТВАМИ
ОБЪЕДИНЕНИЕ МНОЖЕСТВ
ПЕРЕСЕЧЕНИЕ МНОЖЕСТВ
НАХОДИТЬ
ОБЪЕДИНЕНИЕ
МНОЖЕСТВ
1
НАХОДИТЬ
ПЕРЕСЕЧЕНИЕ
МНОЖЕСТВ
2
4
ИЗОБРАЖАТЬ С
ПОМОЩЬЮ КРУГОВ
ЭЙЛЕРА-ВЕННА
РЕШАТЬ ЗАДАЧИ С
ИСПОЛЬЗОВАНИЕМ
ИМЕЮЩИХСЯ ЗНАНИЙ

























































 Математика
Математика








