Похожие презентации:
Кладистика. Метод максимальной парсимонии. Метод присоединения соседей
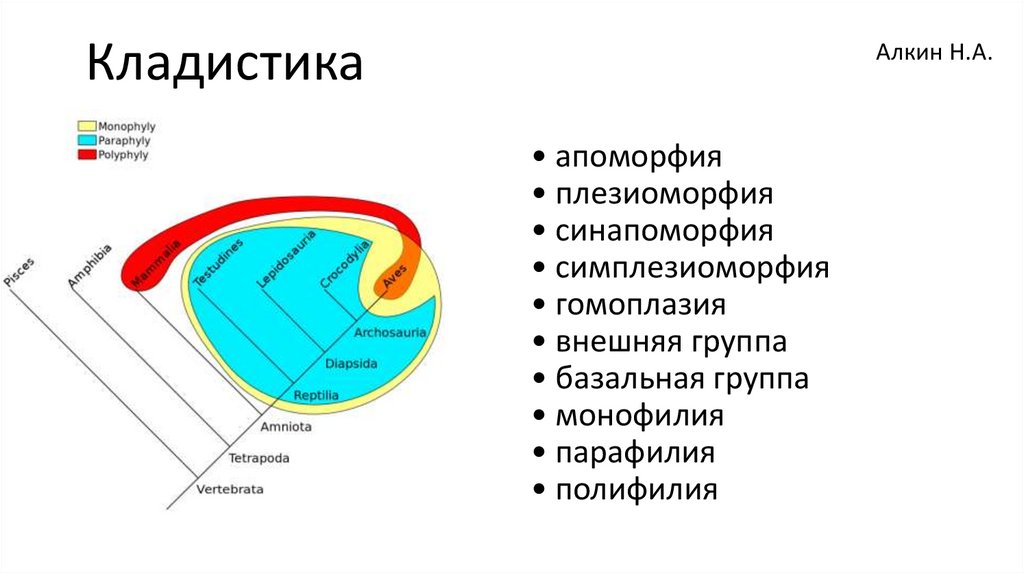
1. Кладистика
Алкин Н.А.• апоморфия
• плезиоморфия
• синапоморфия
• симплезиоморфия
• гомоплазия
• внешняя группа
• базальная группа
• монофилия
• парафилия
• полифилия
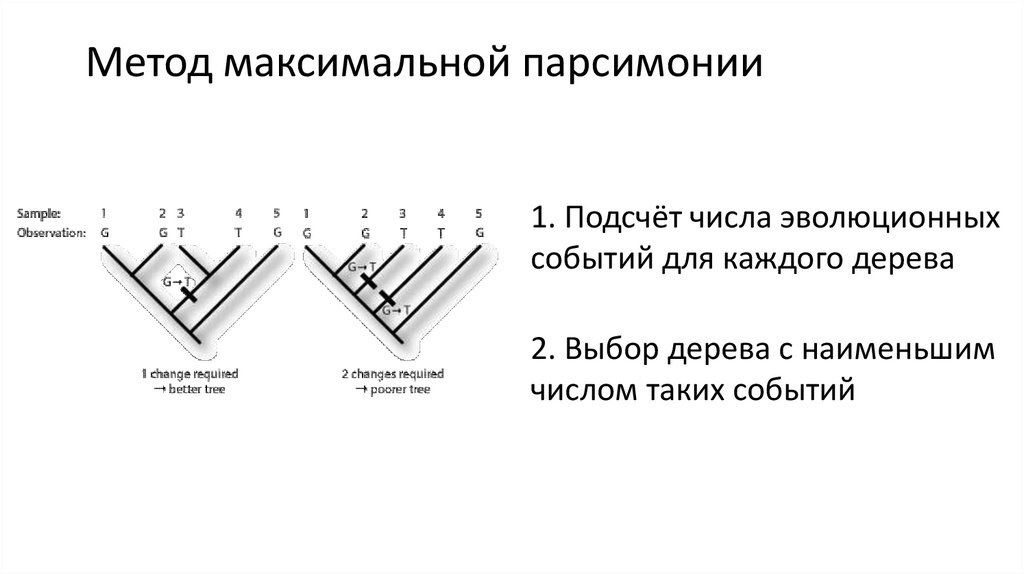
2. Метод максимальной парсимонии
1. Подсчёт числа эволюционныхсобытий для каждого дерева
2. Выбор дерева с наименьшим
числом таких событий
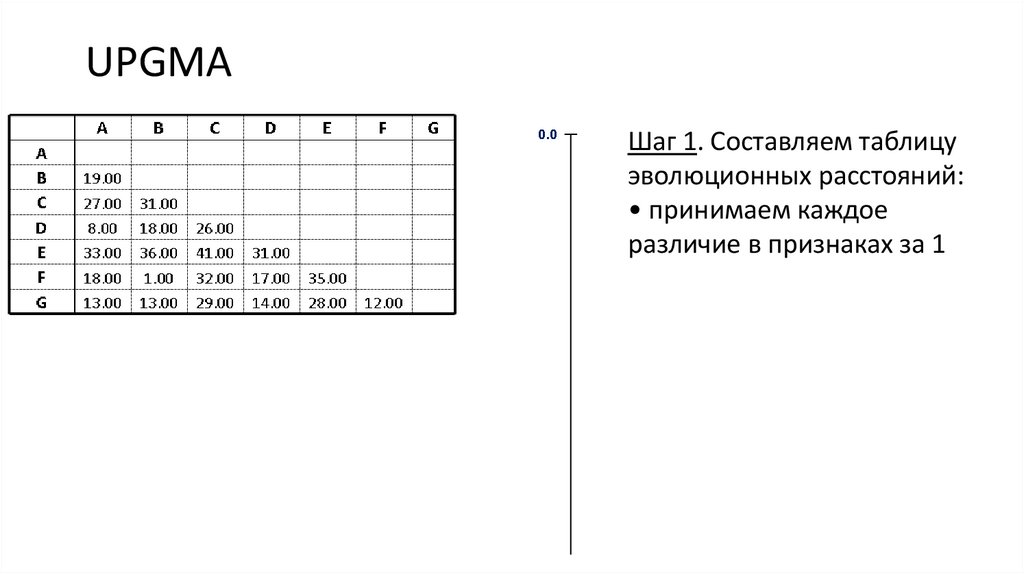
3. UPGMA
Шаг 1. Составляем таблицуэволюционных расстояний:
• принимаем каждое
различие в признаках за 1
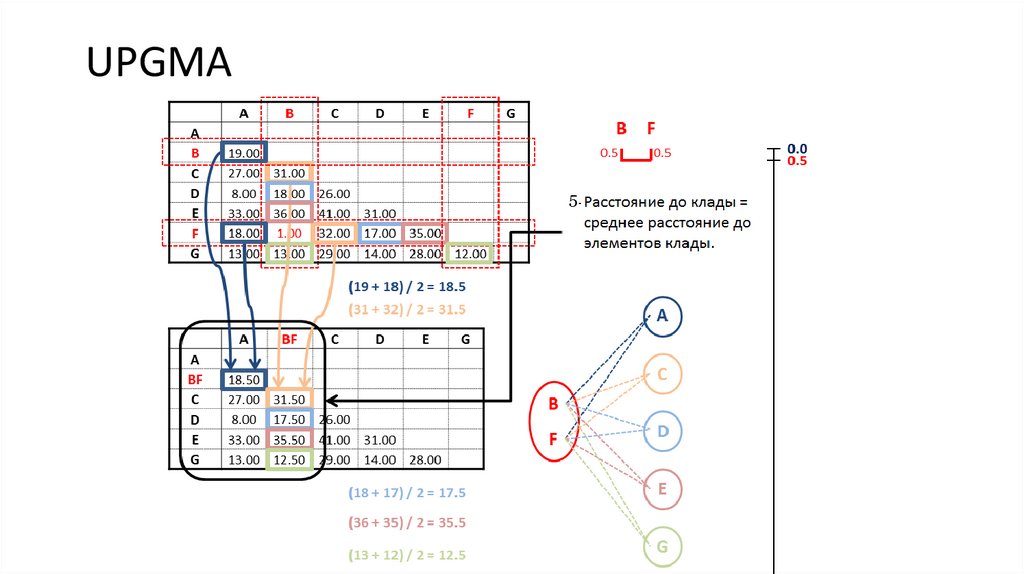
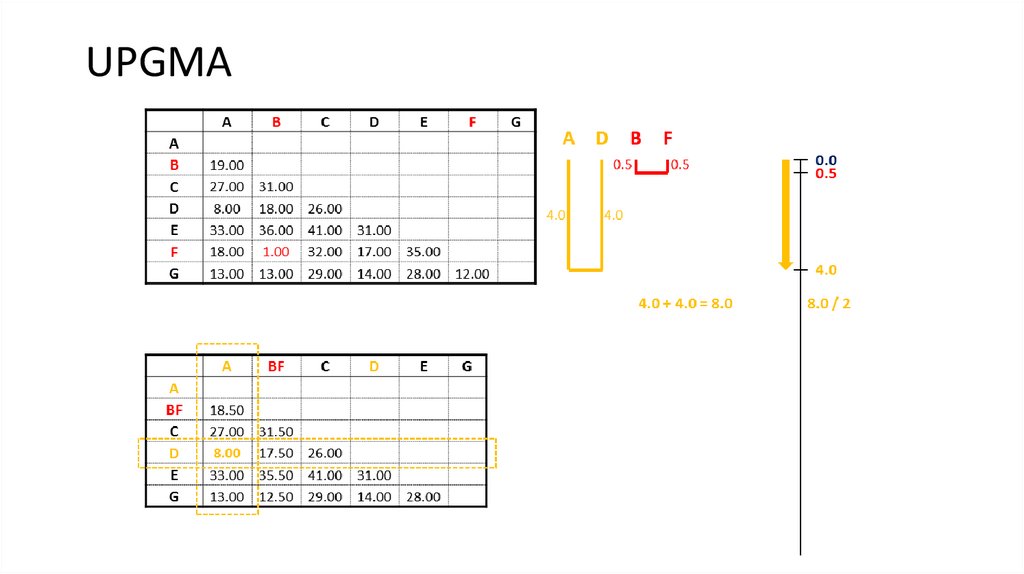
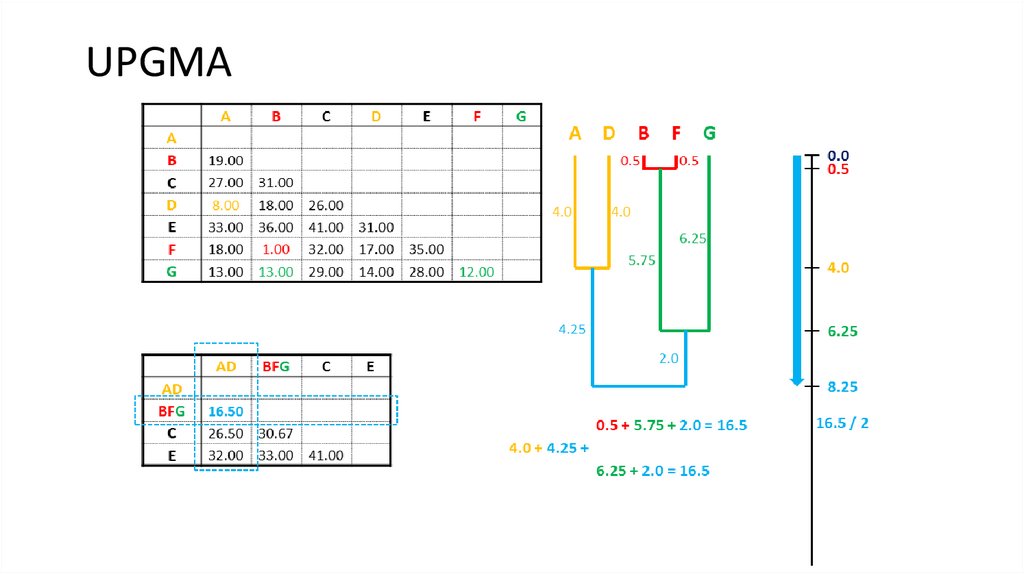
4. UPGMA
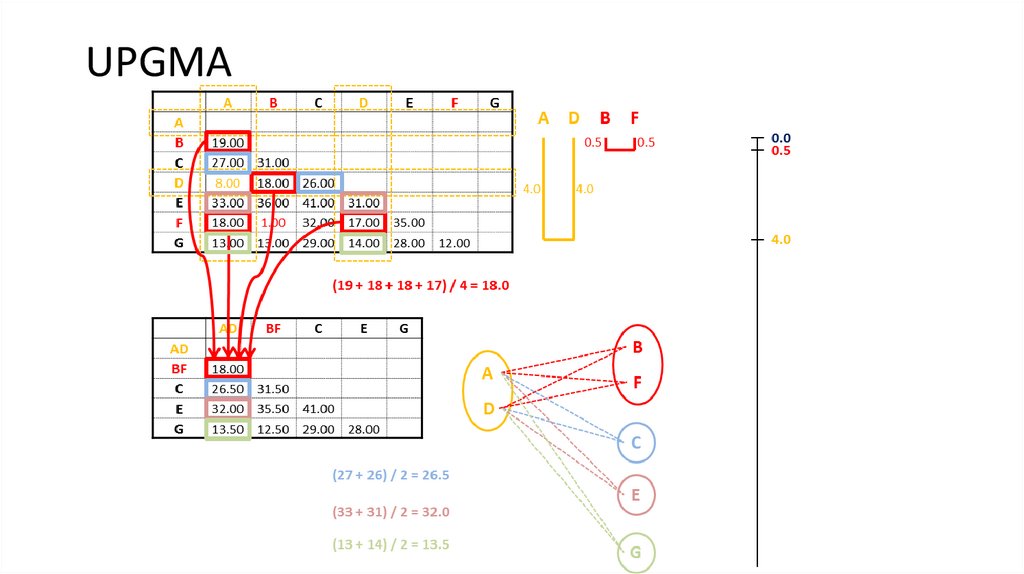
5. UPGMA
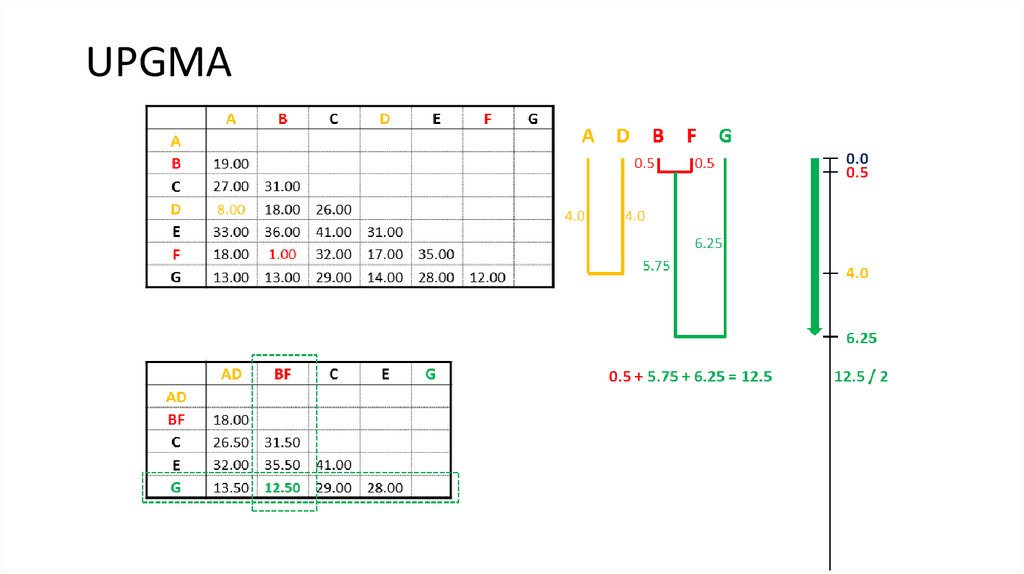
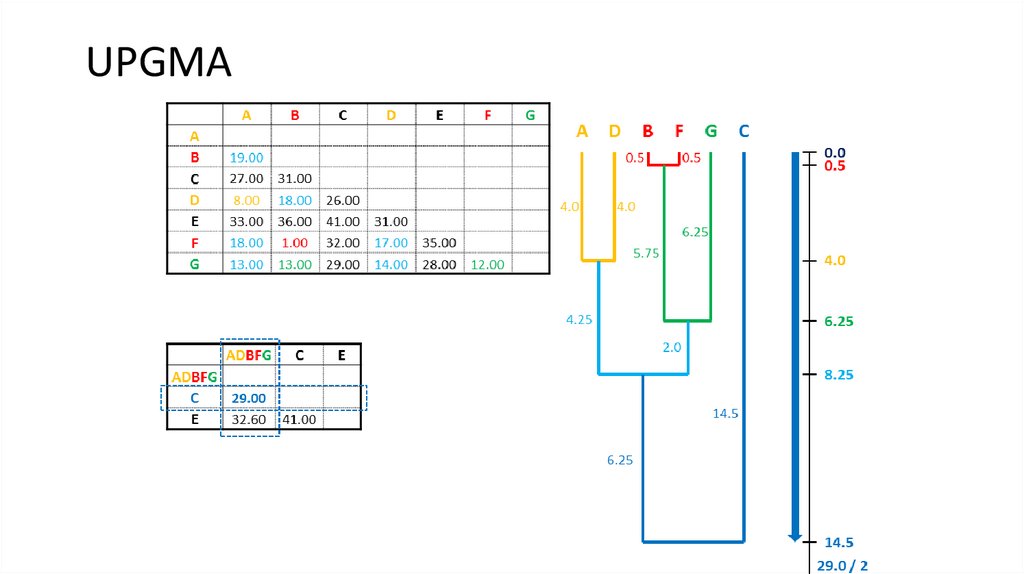
6. UPGMA
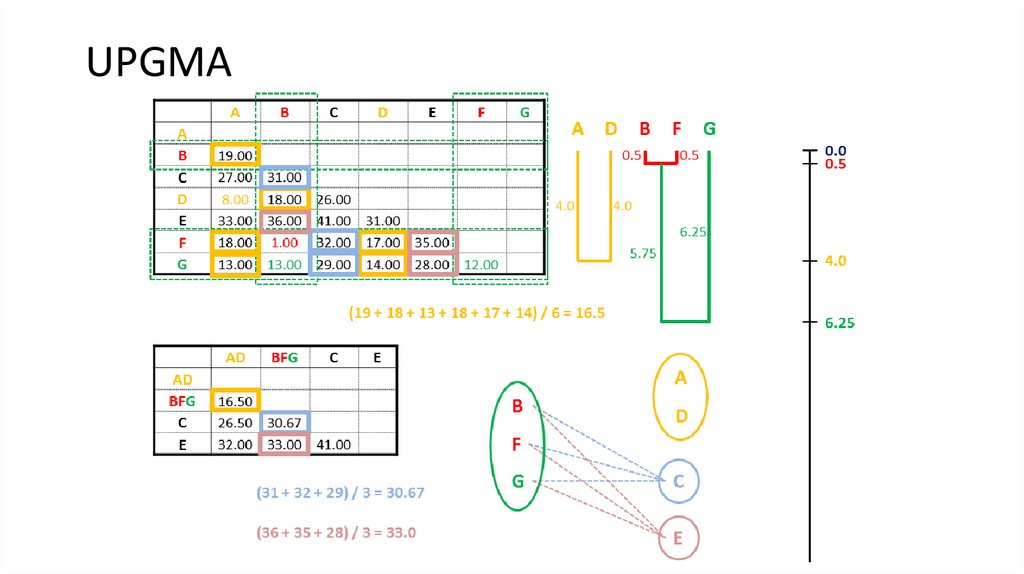
7. UPGMA
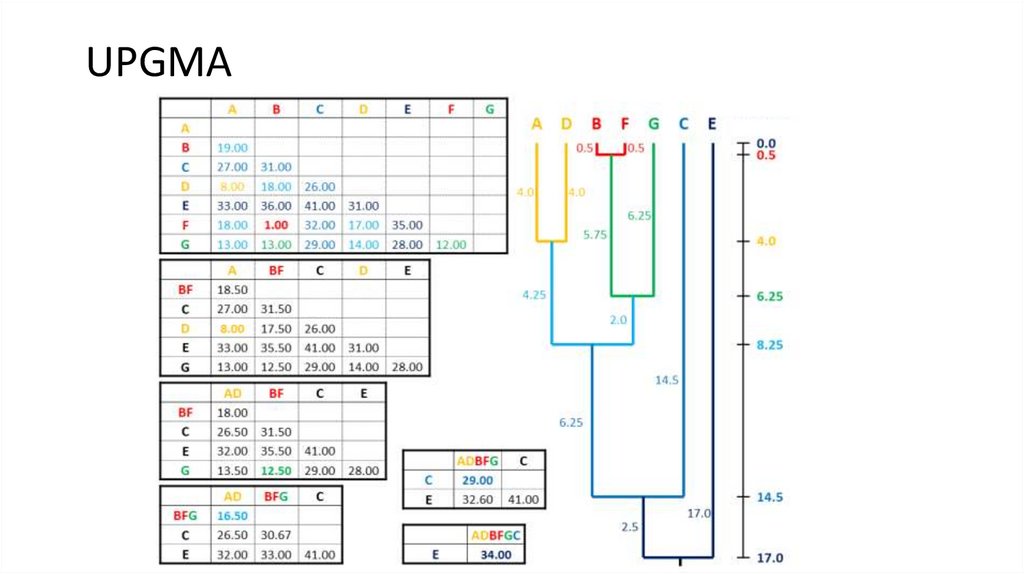
8. UPGMA
9. UPGMA
10. UPGMA
11. UPGMA
12. UPGMA
13. Метод присоединения соседей
1. Построить матрицу расстояний n*n2. Построить Q-матрицу
3. Выбрать наименьшее значение Q
4. Присоединить 2 ветви с Qmin к узлу
5. Найти расстояние от данных ветвей до узла
6. Найти расстояние от остальных ветвей до узла
7. Построить новую матрицу расстояний (n-1)*(n-1)
…
A
A
B
C
D
E
B
C
D
E
5
9
9
8
10
10
9
8
7
3
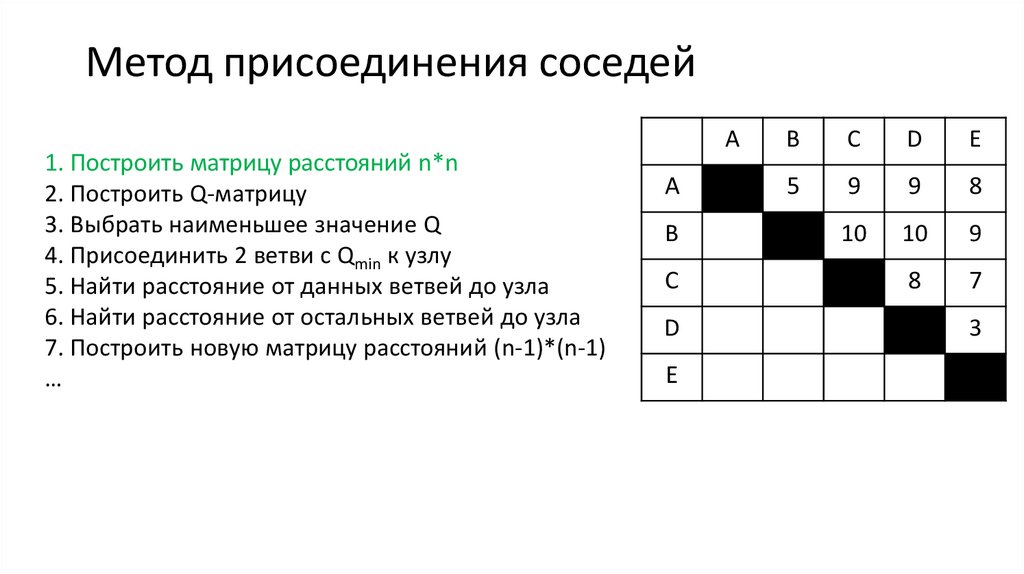
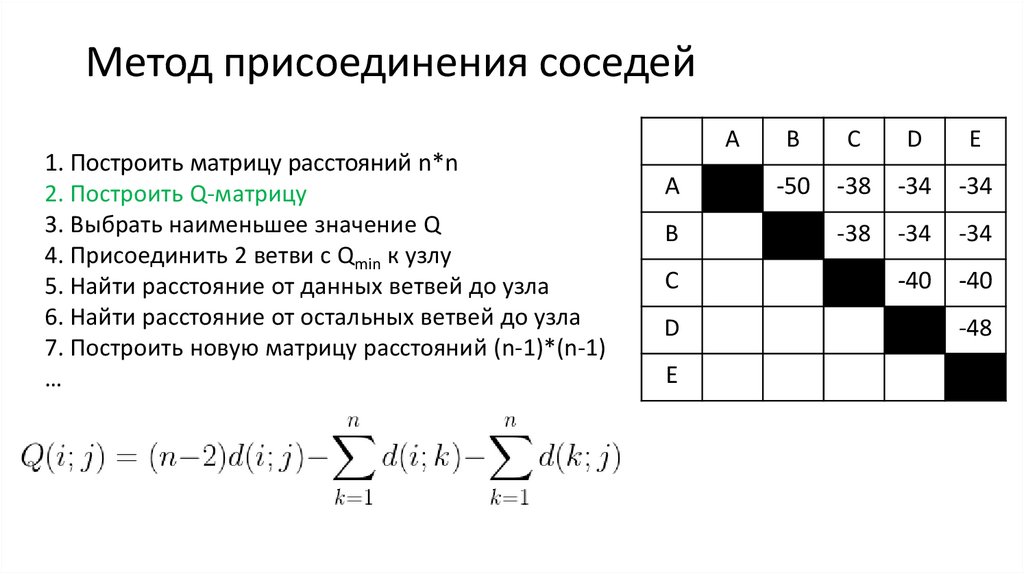
14. Метод присоединения соседей
1. Построить матрицу расстояний n*n2. Построить Q-матрицу
3. Выбрать наименьшее значение Q
4. Присоединить 2 ветви с Qmin к узлу
5. Найти расстояние от данных ветвей до узла
6. Найти расстояние от остальных ветвей до узла
7. Построить новую матрицу расстояний (n-1)*(n-1)
…
A
A
B
C
D
E
B
C
D
E
-50
-38
-34
-34
-38
-34
-34
-40
-40
-48
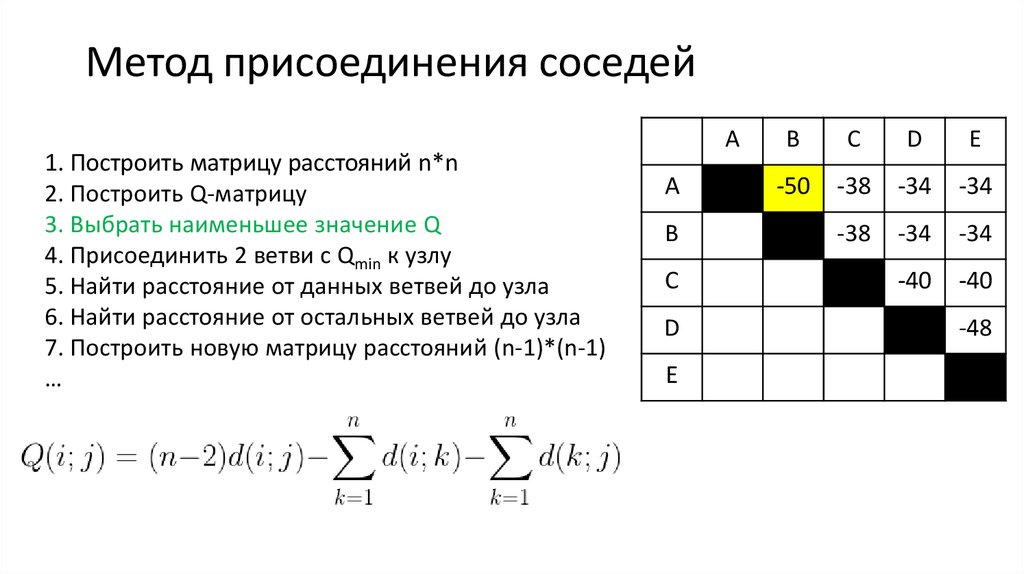
15. Метод присоединения соседей
1. Построить матрицу расстояний n*n2. Построить Q-матрицу
3. Выбрать наименьшее значение Q
4. Присоединить 2 ветви с Qmin к узлу
5. Найти расстояние от данных ветвей до узла
6. Найти расстояние от остальных ветвей до узла
7. Построить новую матрицу расстояний (n-1)*(n-1)
…
A
A
B
C
D
E
B
C
D
E
-50
-38
-34
-34
-38
-34
-34
-40
-40
-48
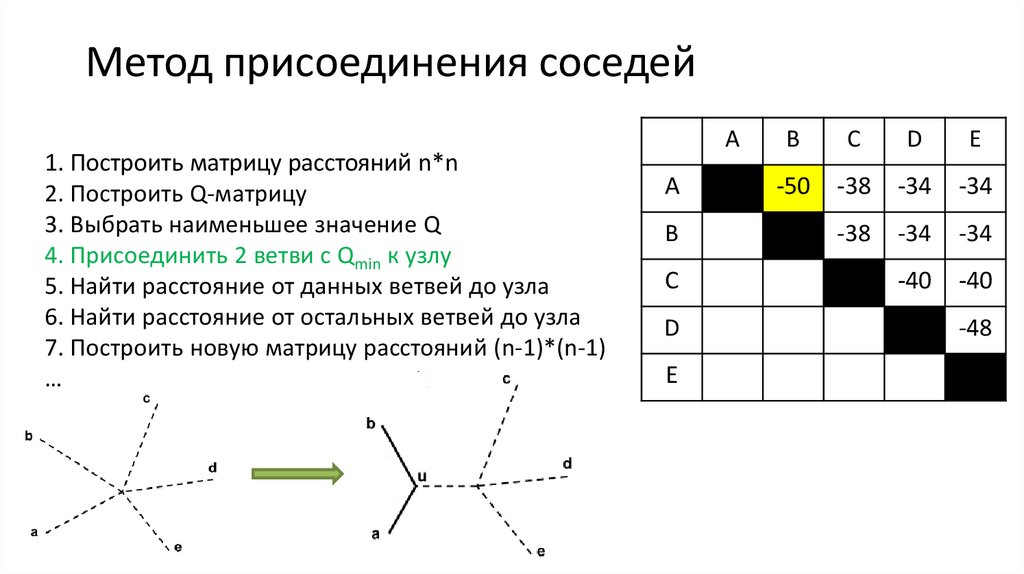
16. Метод присоединения соседей
1. Построить матрицу расстояний n*n2. Построить Q-матрицу
3. Выбрать наименьшее значение Q
4. Присоединить 2 ветви с Qmin к узлу
5. Найти расстояние от данных ветвей до узла
6. Найти расстояние от остальных ветвей до узла
7. Построить новую матрицу расстояний (n-1)*(n-1)
…
A
A
B
C
D
E
B
C
D
E
-50
-38
-34
-34
-38
-34
-34
-40
-40
-48
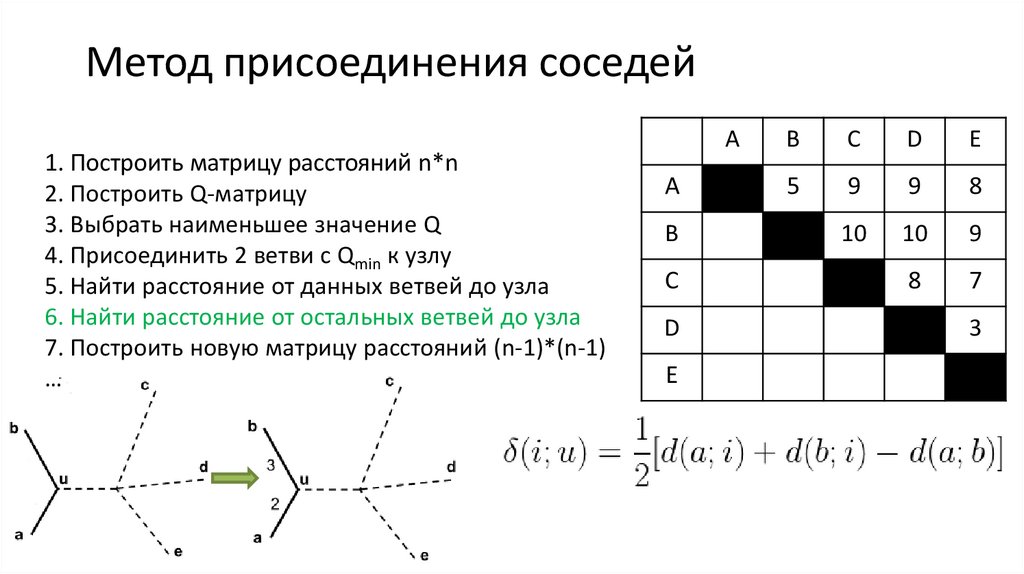
17. Метод присоединения соседей
1. Построить матрицу расстояний n*n2. Построить Q-матрицу
3. Выбрать наименьшее значение Q
4. Присоединить 2 ветви с Qmin к узлу
5. Найти расстояние от данных ветвей до узла
6. Найти расстояние от остальных ветвей до узла
7. Построить новую матрицу расстояний (n-1)*(n-1)
…
A
A
B
C
D
E
B
C
D
E
5
9
9
8
10
10
9
8
7
3
18. Метод присоединения соседей
1. Построить матрицу расстояний n*n2. Построить Q-матрицу
3. Выбрать наименьшее значение Q
4. Присоединить 2 ветви с Qmin к узлу
5. Найти расстояние от данных ветвей до узла
6. Найти расстояние от остальных ветвей до узла
7. Построить новую матрицу расстояний (n-1)*(n-1)
…
A
A
B
C
D
E
B
C
D
E
5
9
9
8
10
10
9
8
7
3
19. Метод присоединения соседей
U1. Построить матрицу расстояний n*n
2. Построить Q-матрицу
3. Выбрать наименьшее значение Q
4. Присоединить 2 ветви с Qmin к узлу
5. Найти расстояние от данных ветвей до узла
6. Найти расстояние от остальных ветвей до узла
7. Построить новую матрицу расстояний (n-1)*(n-1)
…
U
C
D
E
C
D
E
7
7
6
8
7
3
20. Метод присоединения соседей
U1. Построить матрицу расстояний n*n
2. Построить Q-матрицу
3. Выбрать наименьшее значение Q
4. Присоединить 2 ветви с Qmin к узлу
5. Найти расстояние от данных ветвей до узла
6. Найти расстояние от остальных ветвей до узла
7. Построить новую матрицу расстояний (n-1)*(n-1)
…
U
C
D
E
C
D
E
-28
-24
-24
-24
-24
-28
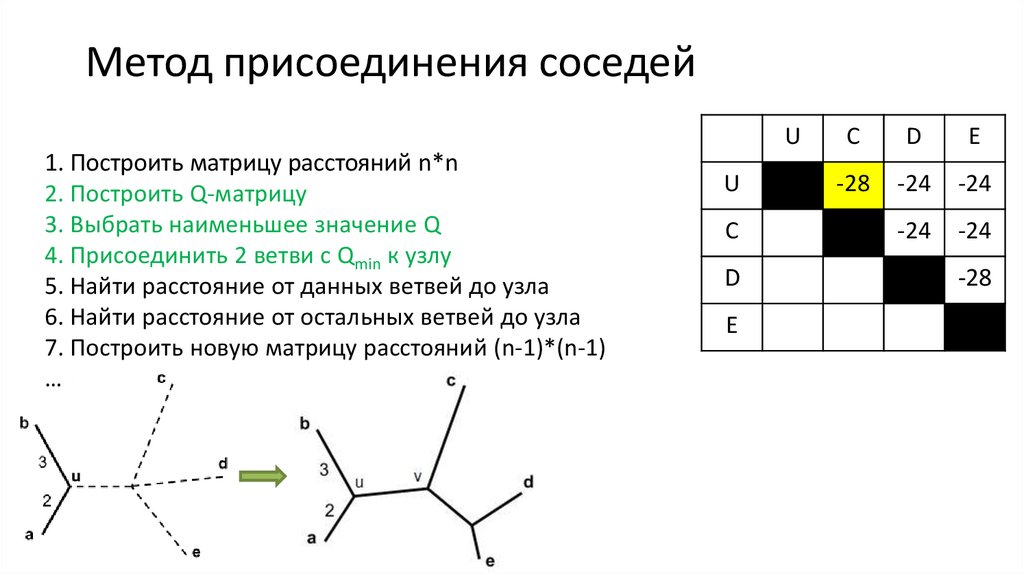
21. Метод присоединения соседей
U1. Построить матрицу расстояний n*n
2. Построить Q-матрицу
3. Выбрать наименьшее значение Q
4. Присоединить 2 ветви с Qmin к узлу
5. Найти расстояние от данных ветвей до узла
6. Найти расстояние от остальных ветвей до узла
7. Построить новую матрицу расстояний (n-1)*(n-1)
…
U
C
D
E
C
D
E
-28
-24
-24
-24
-24
-28
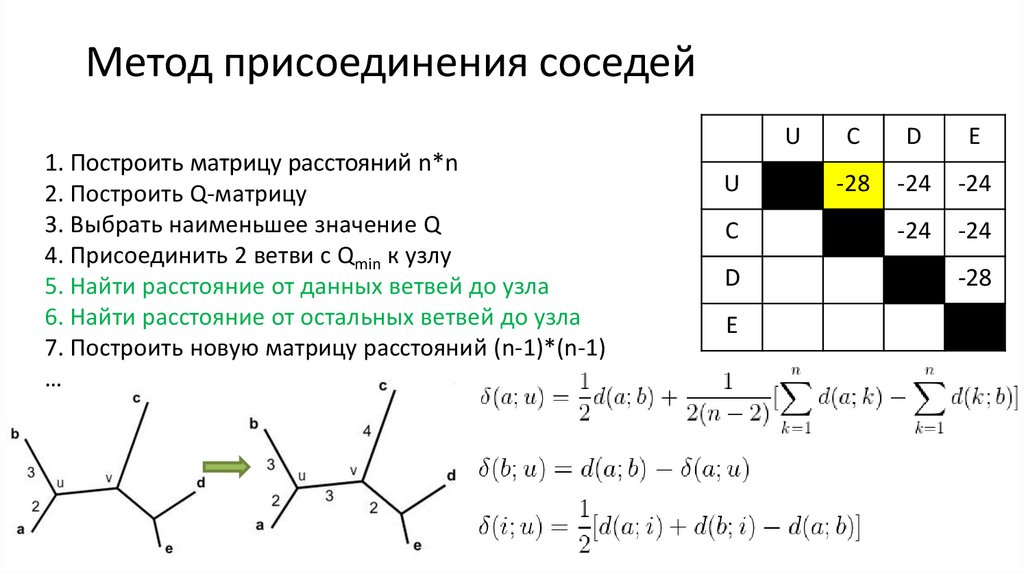
22. Метод присоединения соседей
VV
1. Построить матрицу расстояний n*n
2. Построить Q-матрицу
D
3. Выбрать наименьшее значение Q
4. Присоединить 2 ветви с Qmin к узлу
E
5. Найти расстояние от данных ветвей до узла
6. Найти расстояние от остальных ветвей до узла
7. Построить новую матрицу расстояний (n-1)*(n-1)
…
D
E
V
4
3
V
-10 -10
3
D
-10
E
D
E




 Биология
Биология








