Похожие презентации:
Улучшение оценки числа ребер в задаче Эрдеша-Хайнала однородности 4
1. Об улучшении оценки числа ребер в задаче Эрдеша-Хайнала однородности 4 весна 2016
реберв задаче Эрдеша-Хайнала
однородности 4
весна 2016
2. Свойство B
3. Основные понятия:
4. История вопроса:
5. Известно, что m(2) = 3, a m(3) = 7
6.
7. Постановка задачи:
8. Что уже известно про m(4)
9. "Вопрос о том, насколько можно доверять такому результату, остается открытым. Подводя итоги, мы с твердой уверенностью можем лишь утверждат
что17 m(4) 23“
(А. М. Райгородский, Д. А. Шабанов, Задача Эрдеша– Хайнала о раскрасках
гиперграфов, ее обобщения и смежные проблемы, 2011, 121).
Оценка в 17 ребер была получена в 1993 г. М. Гольдбергом и Х. Расселом
10. Теорема 1. Пусть H = (V, E) произвольный гиперграф однородности 4. Тогда при E < 19. χ(H) = 2
Теорема 1. Пусть H = (V, E) произвольный гиперграф однородности 4.Тогда при E < 19.
χ(H) = 2
11. Нужно только показать, что m13(4) > 18 и m14(4) > 18
Нужно только показать, что m13 (4) > 18 и m14 (4) > 1812.
13. Определение 1. Введем ri как число ребер инцидентных i вершине. Упорядочим вершины: r1 r2 . . . rv.
Определение 1. Введем ri как число ребер инцидентных iвершине. Упорядочим вершины: r1 r2 . . . r v .
14. Доказательство:
15. Теорема 4. Пусть H(V, E) — произвольный гиперграф : ∀i,j∃e:v_i∈e,v_j∈e, |E| = 18, k = 4, |V | = 13 и r1 = 5. Тогда χ(H) = 2
Теорема 4. Пусть H(V, E) — произвольный гиперграф : , |E| = 18,k = 4, |V | = 13 и r1 = 5. Тогда
χ(H) = 2
16. Доказательство. Напомним, что 5 = r1 r2 · · · r13, поэтому . . Пока просто запомним такой результат.
Доказательство. Напомним, что 5 = r1 r2 · · · r13 , поэтому.
Пока просто запомним такой результат.
.
17. Cлучай 1. rc =7
18. . |V|=13, r_{1}=4 Под сбалансированной раскраской будем понимать отображение φ : {V } → {Black, White} :|#VBlack − #VWhite|≤1
|V|=13, r_{1}=4Под сбалансированной раскраской будем понимать отображение
φ : {V } → {Black, White} :|#VBlack − # V White |1
19.
20. Доказательство. Докажем, что block4,13 111. Заметим, что по построению ∀ i, j vi ∩ vj ∅, поэтому ∀ i ∈ [2, 13] |v1 ∩ vi| = 1.
21. Число сбалансированных раскрасок двенадцати вершин равно 1/2 · Число раскрасок при наличии хотя бы одного одноцветного ребра-
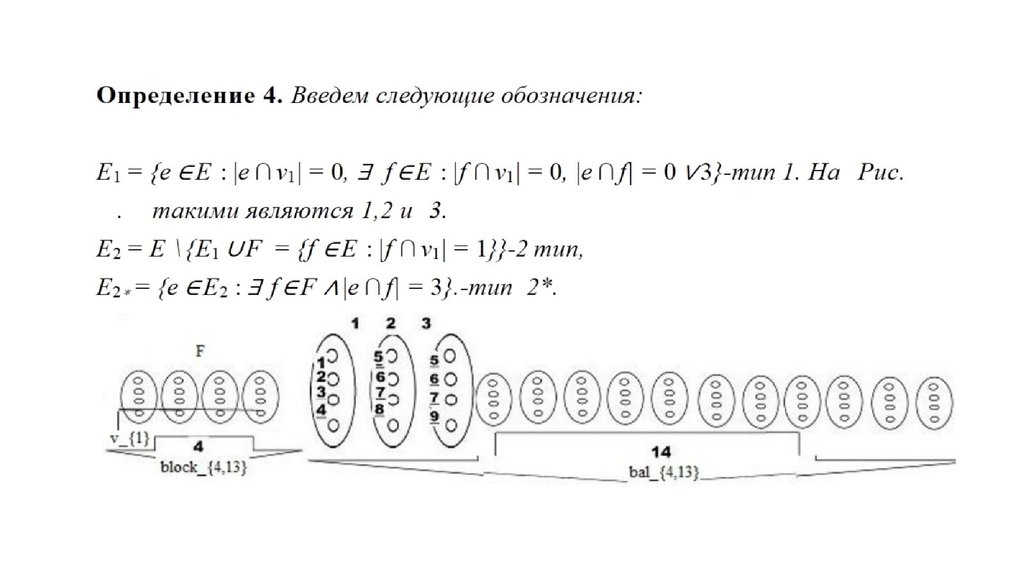
22. Определение 4. Введем следующие обозначения: E1 = {e ∈ E : |e ∩ v1| = 0, ∃ f ∈ E : |f ∩ v1| = 0, |e ∩ f| = 0 ∨ 3}-тип 1. На Рис. . такими являются 1,2 и 3. E2 = E \ {E1 ∪ F = {f
E 1 = {e ∈ E : |e ∩ v1| = 0, ∃ f ∈ E : |f ∩ v1| = 0, |e ∩ f| = 0 ∨ 3}-тип 1. На Рис..
такими являются 1,2 и 3.
E 2 = E \ {E1 ∪ F = {f ∈ E : |f ∩ v1| = 1}}-2 тип,
E2 ∗ = {e ∈ E 2 : ∃ f ∈ F ∧ |e ∩ f| = 3}.-тип 2*.
23. Теорема 3. Пусть H = (V, E) произвольный гиперграф однородности 4 с |E| = 18, |V | = 13 и r1 = 4. Тогда χ(H) = 2 Доказательство. Вначале докажем две технические
E| = 18, |V | = 13 и r1 = 4. Тогдаχ(H) = 2
Доказательство. Вначале докажем две технические леммы
24. Лемма 2. Найдется 19 блокирующих раскрасок для v1 при которых одноцветно зафиксированное ребро типа 2*.
25. Лемма 3. Либо найдется ребро типа 2, не являющееся типом 2*, либо(неисключающее) ∆4,13 > 0
Лемма 3. Либо найдется ребро типа 2, не являющееся типом 2*,либо(неисключающее) ∆ 4,13 > 0
26. Алгоритм 1: построение правильной раскраски, в случае, когда найдется ребро e ∈ E2 \ E2∗
27.
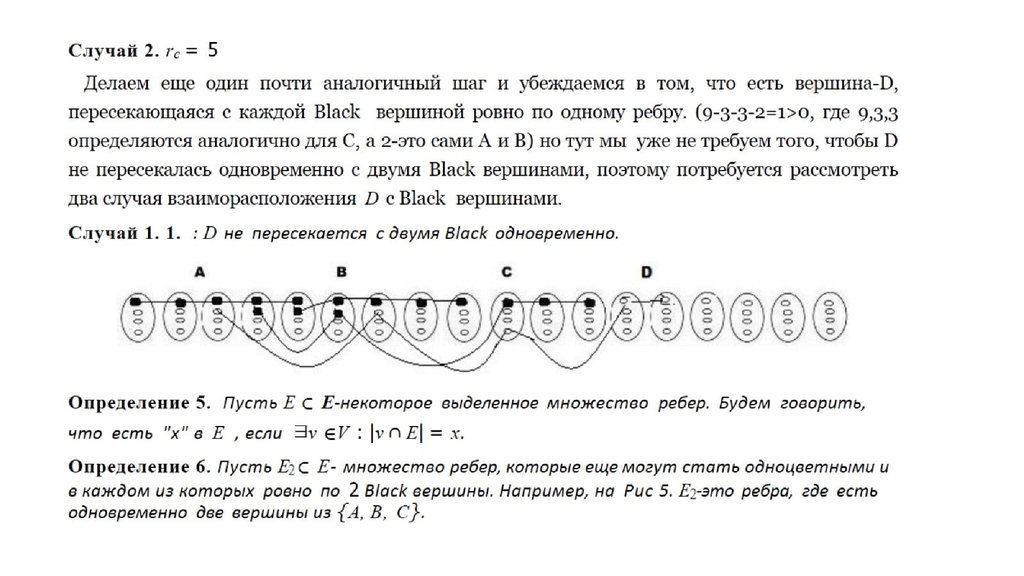
28. v∗alone = 2 Случай 1 ( e пересекается со всеми фиксированными) .
29.
30. v∗alone = 3
31. Возвращаемся к случаю r=5
32.
33.
34.
35.
36.
37.
38.
39. Получение противоречия
40.
41. Cлучай 3. rc =6
42. Таблица всевозможных пересечений D
43. n = 1: нашли вершину D, являющуюся аналогом C из случая 1. n = 2, rD = 6: остается 3 одноцветных ребра и 7 ребер, где по две Black вершины, а такие случаи уж
вершины, а такие случаи уже умеем раскрашивать.n = 3: Раскрасить можно: 4 варианта покраски одной вершины в последнем
ребре против двух потенциально возможных ребер, где по три Black вершины.
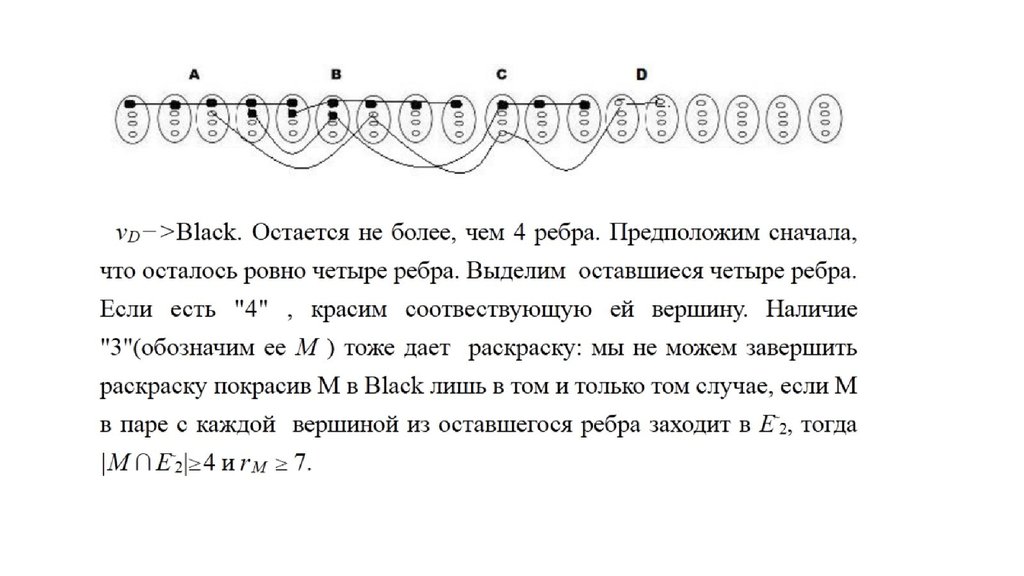
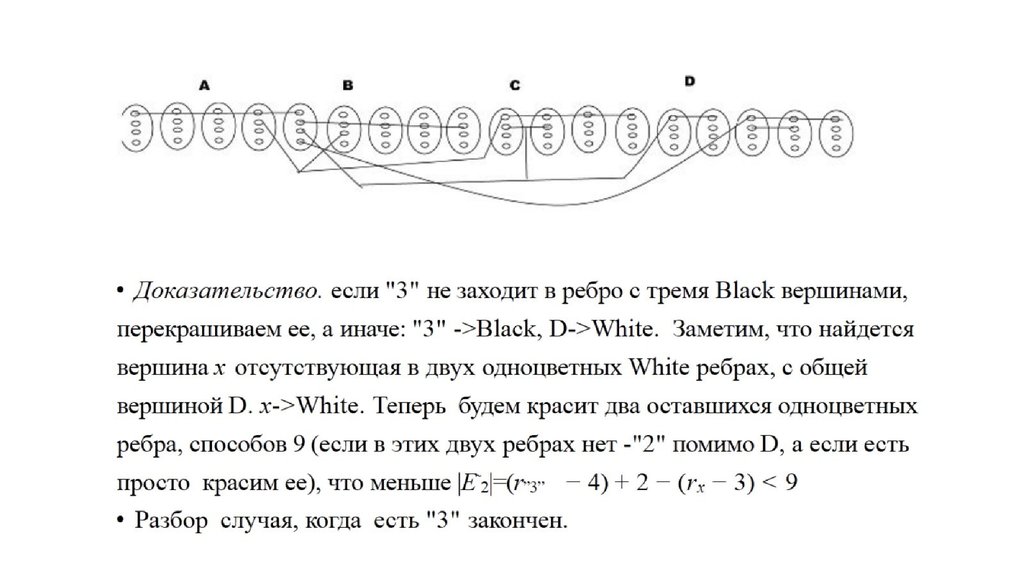
n = 4 : Преположим наличие "3"и докажем возможность правильной
раскраски при таком случае:










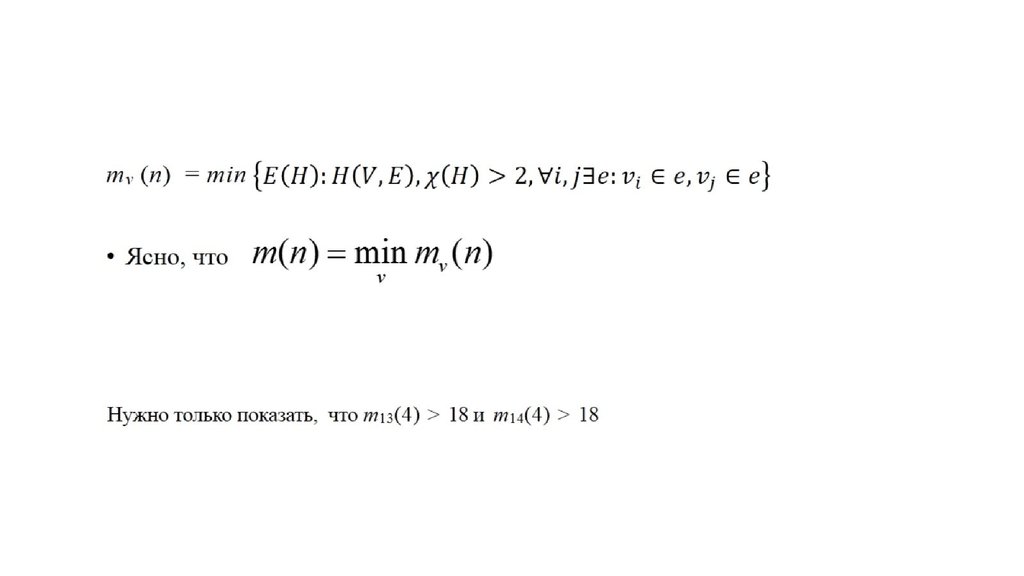








![Доказательство. Докажем, что block4,13 111. Заметим, что по построению ∀ i, j vi ∩ vj ∅, поэтому ∀ i ∈ [2, 13] |v1 ∩ vi| = 1. Доказательство. Докажем, что block4,13 111. Заметим, что по построению ∀ i, j vi ∩ vj ∅, поэтому ∀ i ∈ [2, 13] |v1 ∩ vi| = 1.](https://cf.ppt-online.org/files/slide/2/2HQPrhEas5CY7bWvI3KfLqiBTw9FZzuVX41tgj/slide-19.jpg)





















![[r1 = 5, v = 14] [r1 = 5, v = 14]](https://cf.ppt-online.org/files/slide/2/2HQPrhEas5CY7bWvI3KfLqiBTw9FZzuVX41tgj/slide-45.jpg)




 Математика
Математика








