Балансировка деревьев

1. Балансировка деревьев

БАЛАНСИРОВКА
ДЕРЕВЬЕВ
© 2015, Serge Kashkevich

2. Недостаток бинарных поисковых деревьев

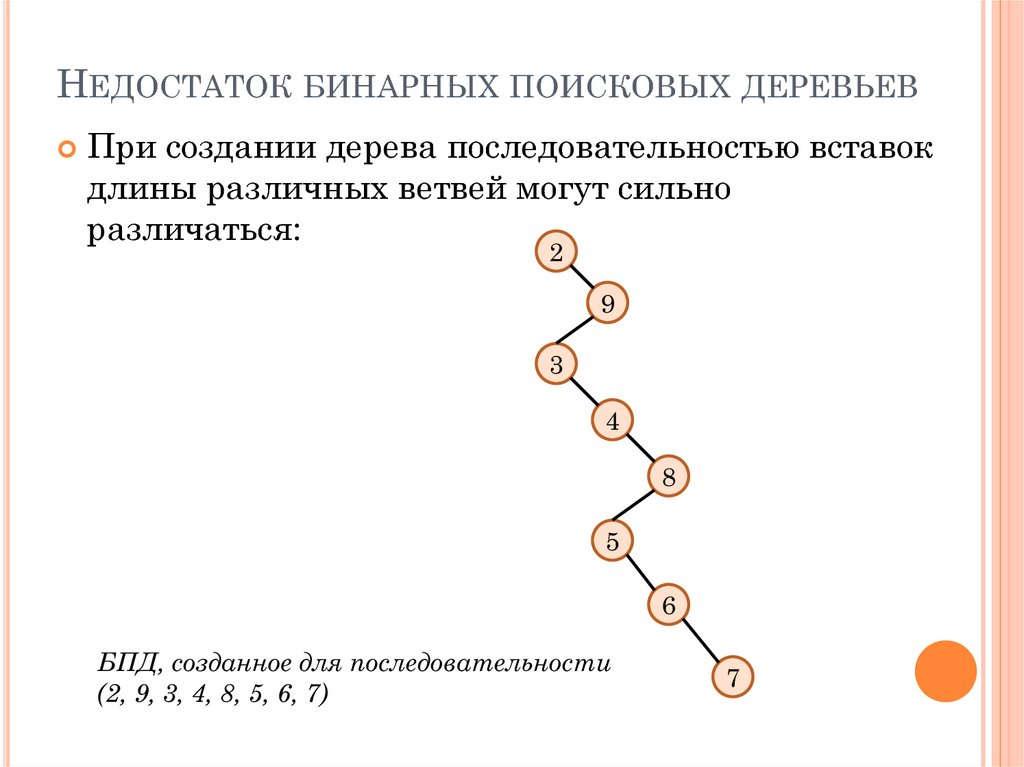
НЕДОСТАТОК БИНАРНЫХ ПОИСКОВЫХ ДЕРЕВЬЕВ
При создании дерева последовательностью вставок
длины различных ветвей могут сильно
различаться:
2
9
3
4
8
5
6
БПД, созданное для последовательности
(2, 9, 3, 4, 8, 5, 6, 7)
7

3. Подходы к решению проблемы

ПОДХОДЫ К РЕШЕНИЮ ПРОБЛЕМЫ
Создать древовидные структуры, у которых
длины ветвей будут не сильно отличаться друг
от друга (сбалансированные деревья)
При этом поддержание сбалансированности
должно выполняться с трудоёмкостью не
большей, чем O(log N).
ВАРИАНТЫ РЕШЕНИЯ:
АВЛ-деревья;
сильно ветвящиеся деревья;
красно-чёрные деревья

4. АВЛ-ДЕРЕВЬЯ

АВЛ-дерево (почти сбалансированное дерево) –
двоичное поисковое дерево, для каждой вершины
которого высота её двух поддеревьев различается не
более чем на 1.
АВЛ-деревья названы по первым буквам фамилий их изобретателей, Г.
М. Адельсона-Вельского и Е. М. Ландиса, которые впервые предложили
использовать АВЛ-деревья в 1962 году.

5. Показатель баланса вершины АВЛ-дерева

ПОКАЗАТЕЛЬ БАЛАНСА ВЕРШИНЫ АВЛДЕРЕВА
Для каждой вершины дерева будем хранить
показатель её баланса:
-1, если левое поддерево длиннее правого на 1;
0, если высоты левого и правого поддерева
равны;
+1, если правое поддерево длиннее левого на 1;
-2, если левое поддерево длиннее правого на 2;
+2, если правое поддерево длиннее левого на 2.
В двух последних случаях будем считать, что
баланс дерева нарушен в этой вершине

6. Пример АВЛ-дерева с наихудшей балансировкой

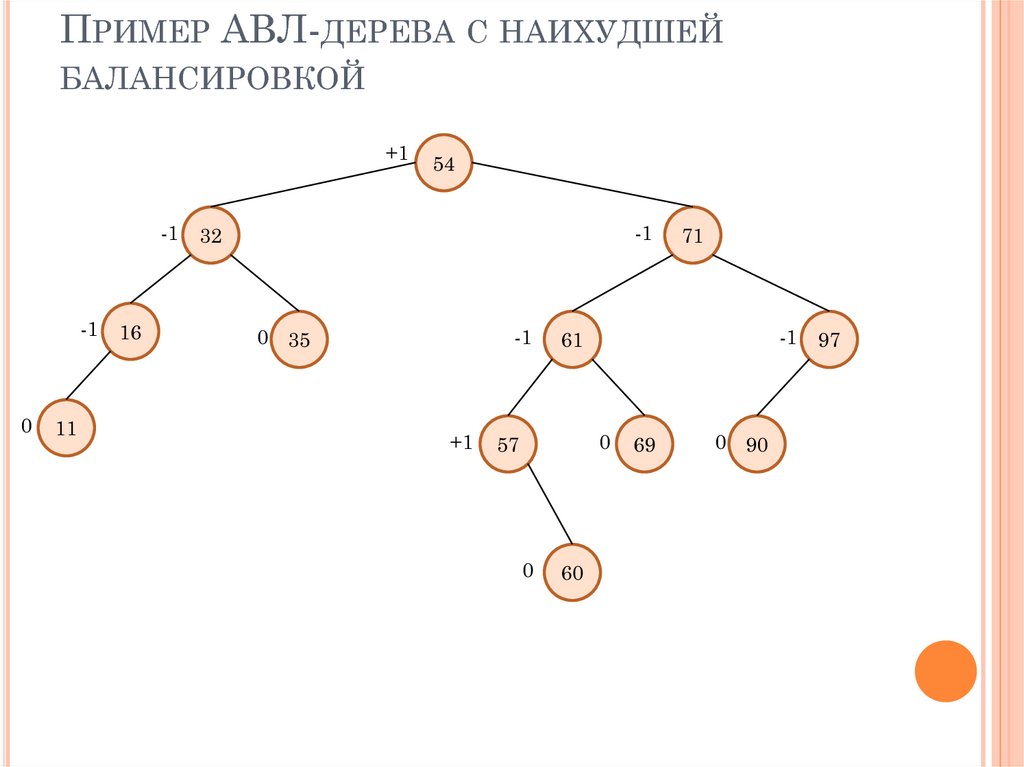
ПРИМЕР АВЛ-ДЕРЕВА С НАИХУДШЕЙ
БАЛАНСИРОВКОЙ
+1
-1
-1
0
11
16
54
-1
32
0 35
-1
+1
-1
61
0
57
0
71
60
69
0 90
97

7. Оценка высоты АВЛ-дерева в зависимости от числа вершин

ОЦЕНКА ВЫСОТЫ АВЛ-ДЕРЕВА В
ЗАВИСИМОСТИ ОТ ЧИСЛА ВЕРШИН
В идеальном случае (высоты всех поддеревьев
равны)
H (n) log 2 (n 1) (äëÿ n 2k 1)
В наихудшем случае (высоты поддеревьев
различаются для каждой вершины)
H (n) 1.4404 * log 2 (n 2) 0.328
В общем случае H ( n) O (log n)
Следовательно, основные операции (поиск,
вставка, удаление) имеют трудоёмкость O(log n)

8. Восстановление сбалансированности вершин АВЛ-дерева после вставки

ВОССТАНОВЛЕНИЕ СБАЛАНСИРОВАННОСТИ
ВЕРШИН АВЛ-ДЕРЕВА ПОСЛЕ ВСТАВКИ
После выполнения вставки необходимо изменить показатели
баланса у вершин, находящихся на ветви дерева, в которую произошла
вставка.
T := добавленная вершина;
while Т <> корень do begin
S := отец T;
if T – левый сын S then
уменьшаем показатель баланса S
else
увеличиваем показатель баланса S;
if показатель баланса S=0 then
break;
if abs(показатель баланса S)=2 then begin
устраняем разбалансированность S, выполняя вращение
или двойное вращение;
break;
end;
T := S;
end;

9. Пояснение остановки при установке показателя баланса в 0

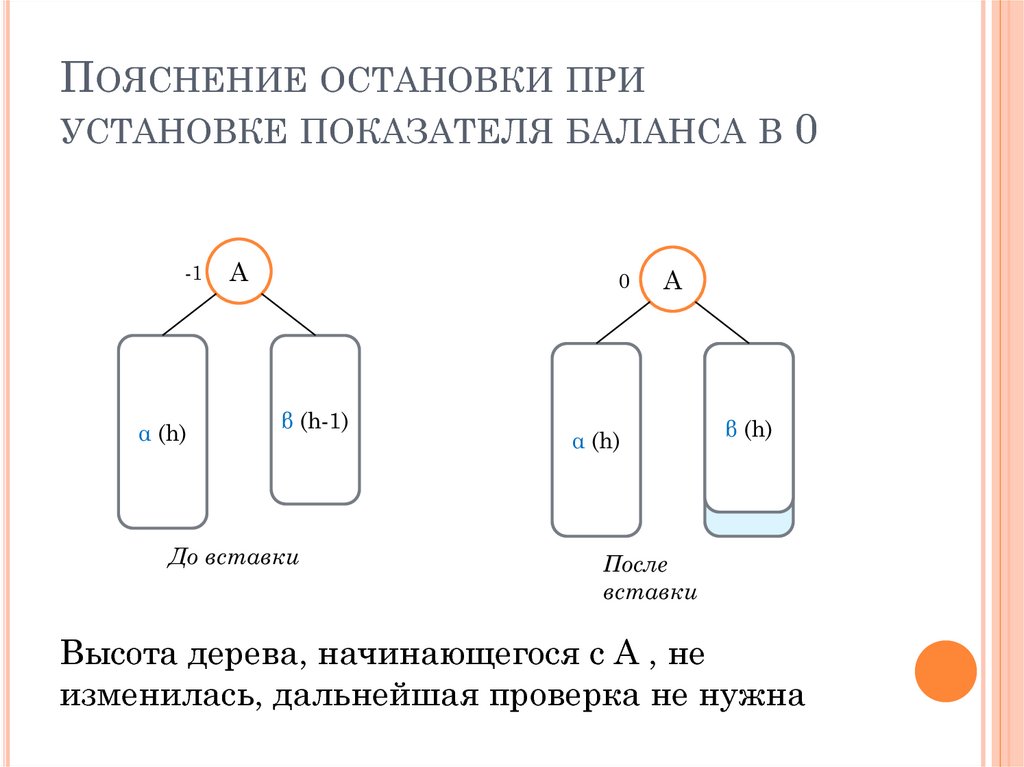
ПОЯСНЕНИЕ ОСТАНОВКИ ПРИ
УСТАНОВКЕ ПОКАЗАТЕЛЯ БАЛАНСА В
-1
α (h)
A
0
β (h-1)
До вставки
0
A
α (h)
β (h)
β
После
вставки
Высота дерева, начинающегося с A , не
изменилась, дальнейшая проверка не нужна

10. Устранение разбалансированности - вращение

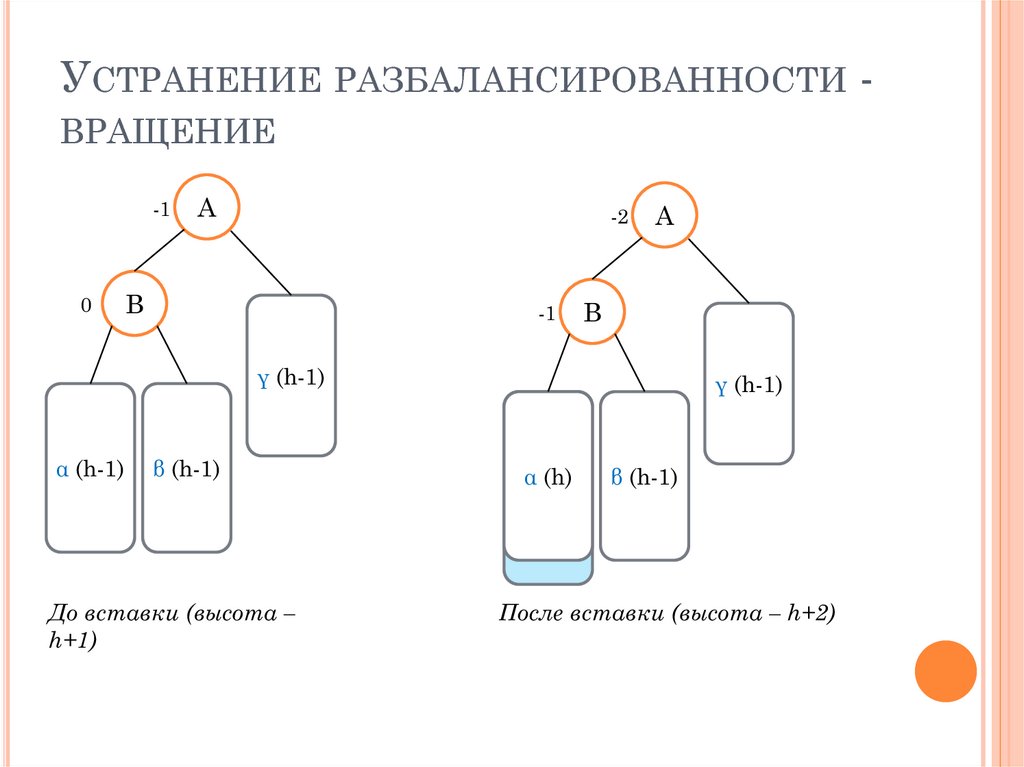
УСТРАНЕНИЕ РАЗБАЛАНСИРОВАННОСТИ ВРАЩЕНИЕ
-1
0
A
-2
B
-1
A
B
γ (h-1)
α (h-1)
β (h-1)
До вставки (высота –
h+1)
γ (h-1)
α (h)
α (h-1)
β (h-1)
После вставки (высота – h+2)

11. Устранение разбалансированности – вращение (продолжение)

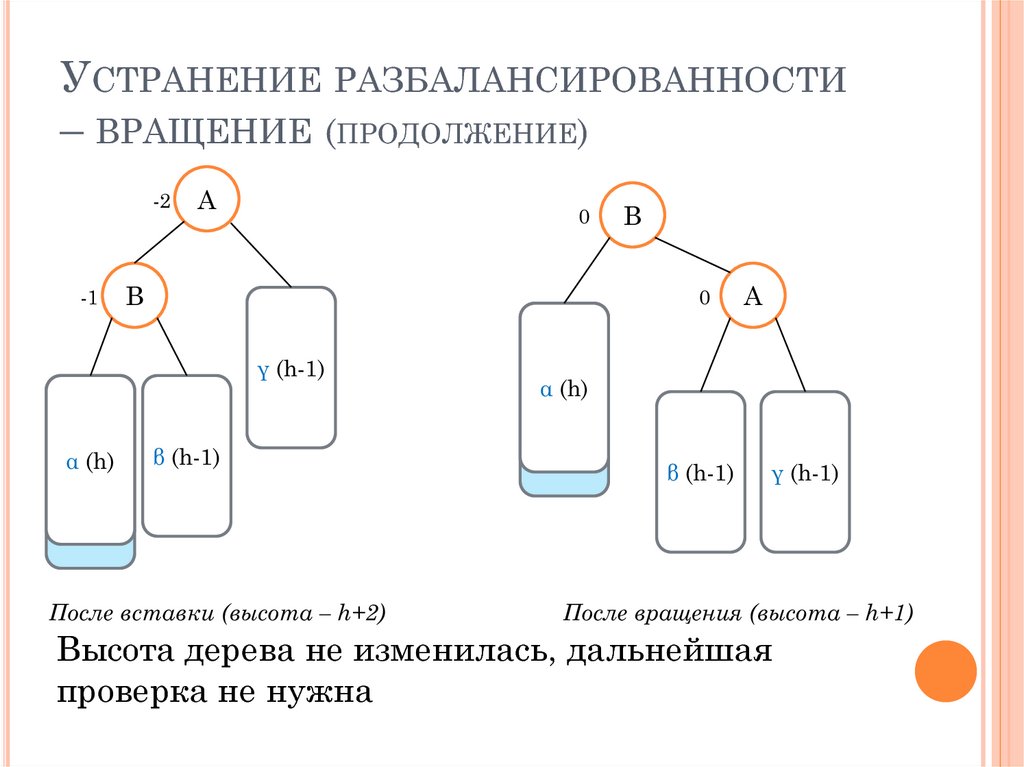
УСТРАНЕНИЕ РАЗБАЛАНСИРОВАННОСТИ
– ВРАЩЕНИЕ (ПРОДОЛЖЕНИЕ)
-2
-1
A
0
B
0
γ (h-1)
α (h)
α (h-1)
B
β (h-1)
После вставки (высота – h+2)
A
α (h)
α (h-1)
β (h-1)
γ (h-1)
После вращения (высота – h+1)
Высота дерева не изменилась, дальнейшая
проверка не нужна

12. Устранение разбалансированности – двойное вращение

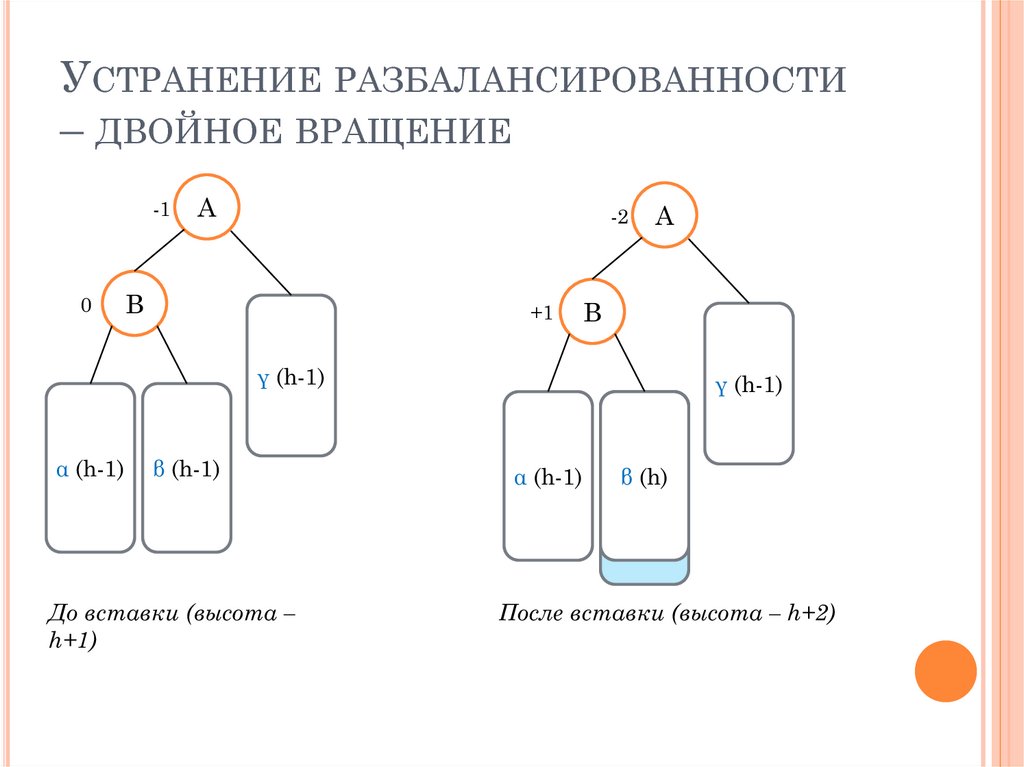
УСТРАНЕНИЕ РАЗБАЛАНСИРОВАННОСТИ
– ДВОЙНОЕ ВРАЩЕНИЕ
-1
0
A
-2
B
+1
A
B
γ (h-1)
α (h-1)
β (h-1)
До вставки (высота –
h+1)
γ (h-1)
α (h-1)
β (h)
α (h-1)
После вставки (высота – h+2)

13. Устранение разбалансированности – двойное вращение (продолжение)

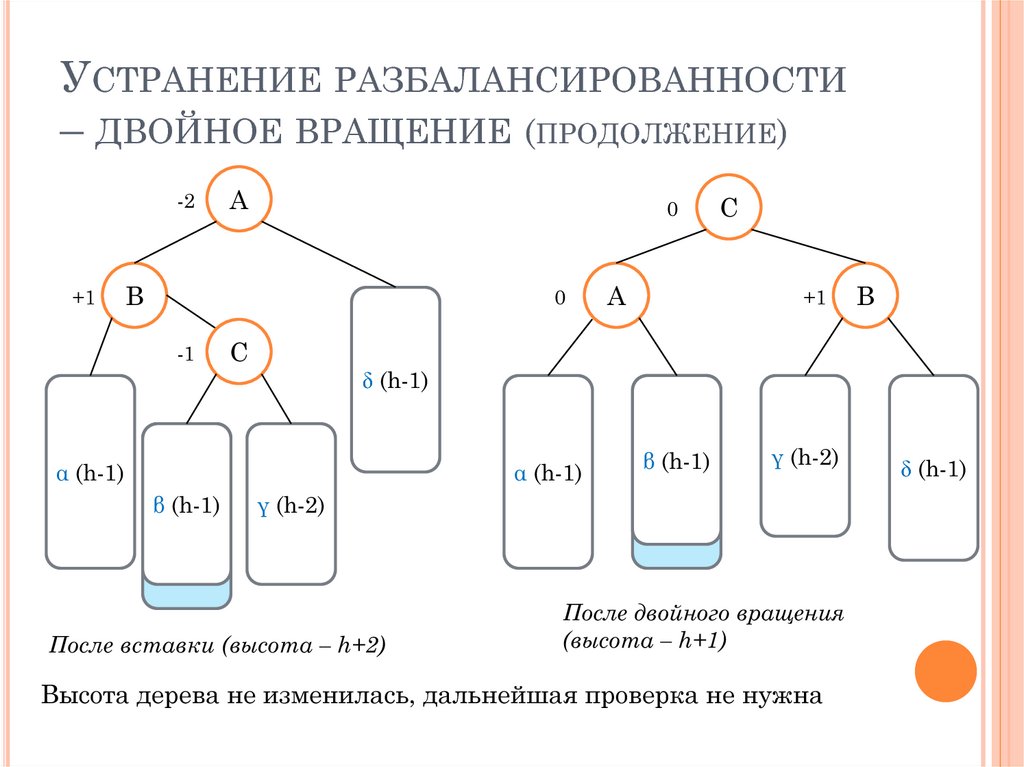
УСТРАНЕНИЕ РАЗБАЛАНСИРОВАННОСТИ
– ДВОЙНОЕ ВРАЩЕНИЕ (ПРОДОЛЖЕНИЕ)
-2
+1
A
0
B
0
-1
С
+1
B
δ (h-1)
α (h-1)
α (h-1)
β (h-1)
α (h-1)
A
С
β (h-1)
α (h-1)
γ (h-2)
γ (h-2)
После вставки (высота – h+2)
После двойного вращения
(высота – h+1)
Высота дерева не изменилась, дальнейшая проверка не нужна
δ (h-1)

14. ВОССТАНОВЛЕНИЕ СБАЛАНСИРОВАННОСТИ ВЕРШИН АВЛ-ДЕРЕВА ПОСЛЕ УДАЛЕНИЯ

ВОССТАНОВЛЕНИЕ
СБАЛАНСИРОВАННОСТИ ВЕРШИН АВЛДЕРЕВА ПОСЛЕ УДАЛЕНИЯ
После выполнения удаления необходимо изменить
показатели баланса у вершин, находящихся на ветви дерева, в
которой произошло удаление.
if дерево не пусто then begin
S := отец удалённой вершины;
T := удалённая вершина;
while true do begin
if T – левый сын S then
увеличиваем показатель баланса S
else
уменьшаем показатель баланса S;
if abs(показатель баланса S)=1 then
break;
if abs(показатель баланса S)=2 then
устраняем разбалансированность S;
if S – корень then
break;
T := S;
S := отец S;
end;
end;

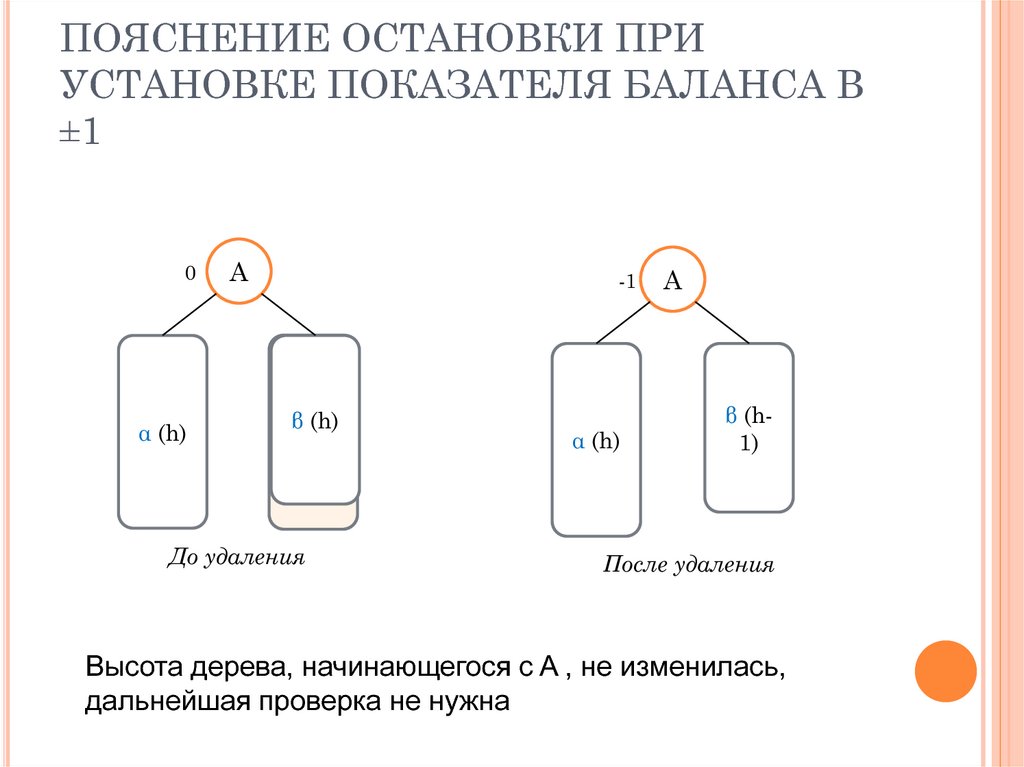
15. ПОЯСНЕНИЕ ОСТАНОВКИ ПРИ УСТАНОВКЕ ПОКАЗАТЕЛЯ БАЛАНСА В ±1

0
α (h)
A
-1
β (h)
До удаления
α (h)
A
β (h1)
После удаления
Высота дерева, начинающегося с A , не изменилась,
дальнейшая проверка не нужна

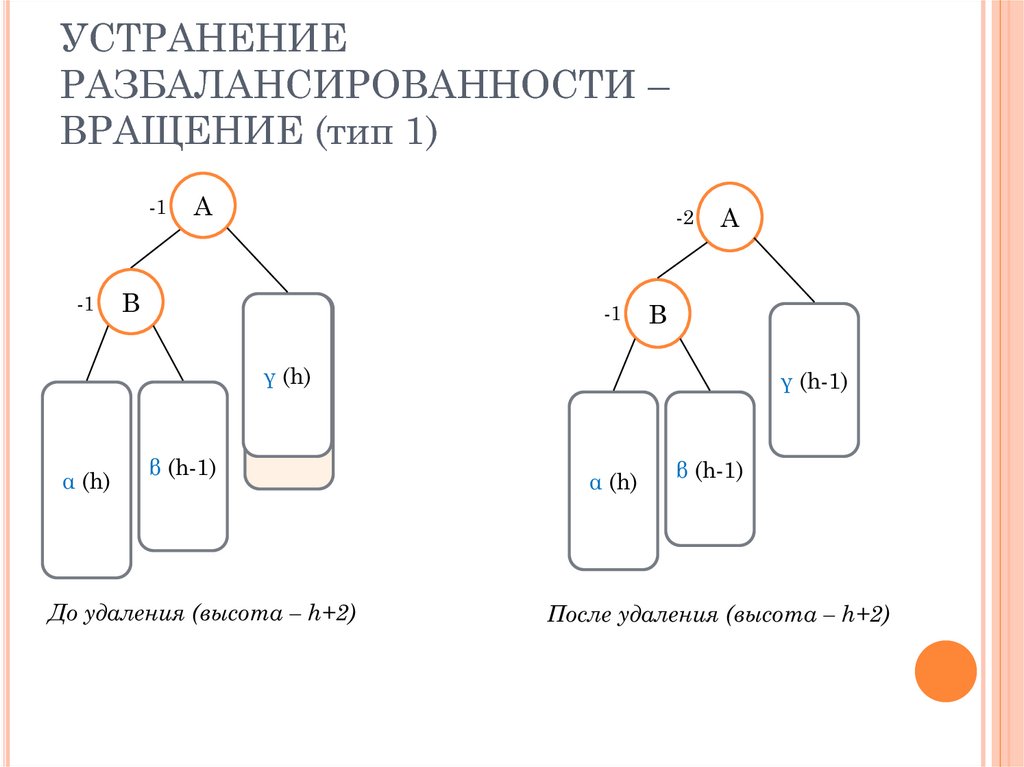
16. УСТРАНЕНИЕ РАЗБАЛАНСИРОВАННОСТИ – ВРАЩЕНИЕ (тип 1)

-1
-1
A
-2
B
-1
A
B
γ (h)
α (h-1)
α (h)
β (h-1)
До удаления (высота – h+2)
γ (h-1)
α (h)
β (h-1)
После удаления (высота – h+2)

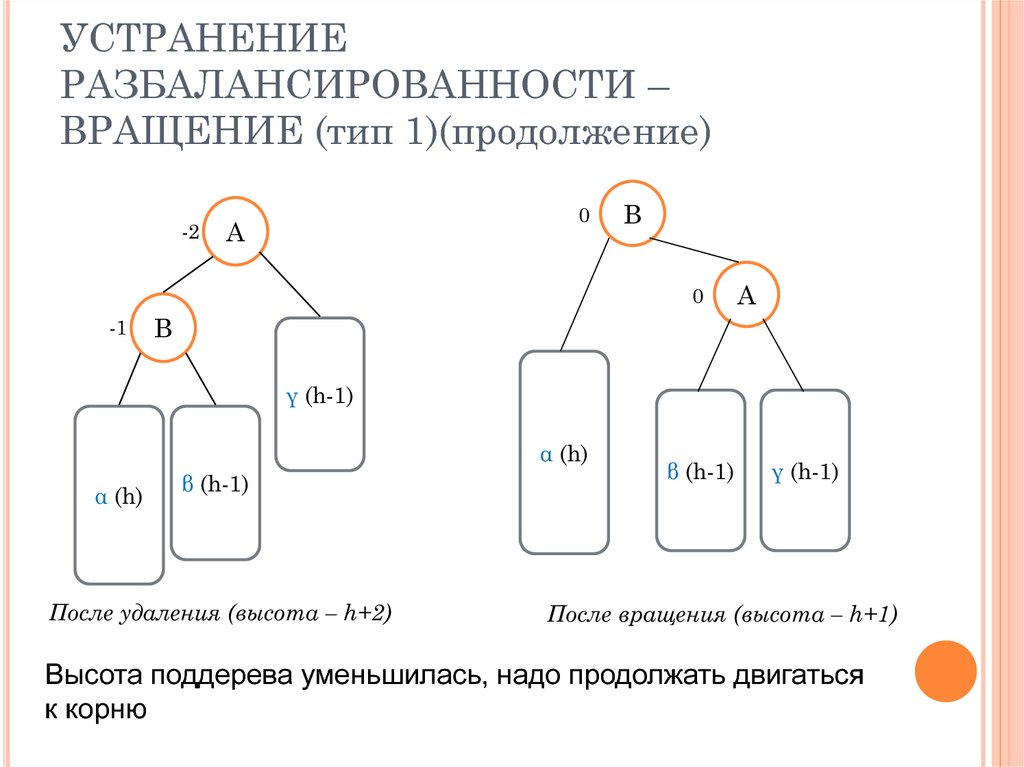
17. УСТРАНЕНИЕ РАЗБАЛАНСИРОВАННОСТИ – ВРАЩЕНИЕ (тип 1)(продолжение)

-2
0
A
B
0
-1
A
B
γ (h-1)
α (h)
α (h)
β (h-1)
После удаления (высота – h+2)
β (h-1)
γ (h-1)
После вращения (высота – h+1)
Высота поддерева уменьшилась, надо продолжать двигаться
к корню

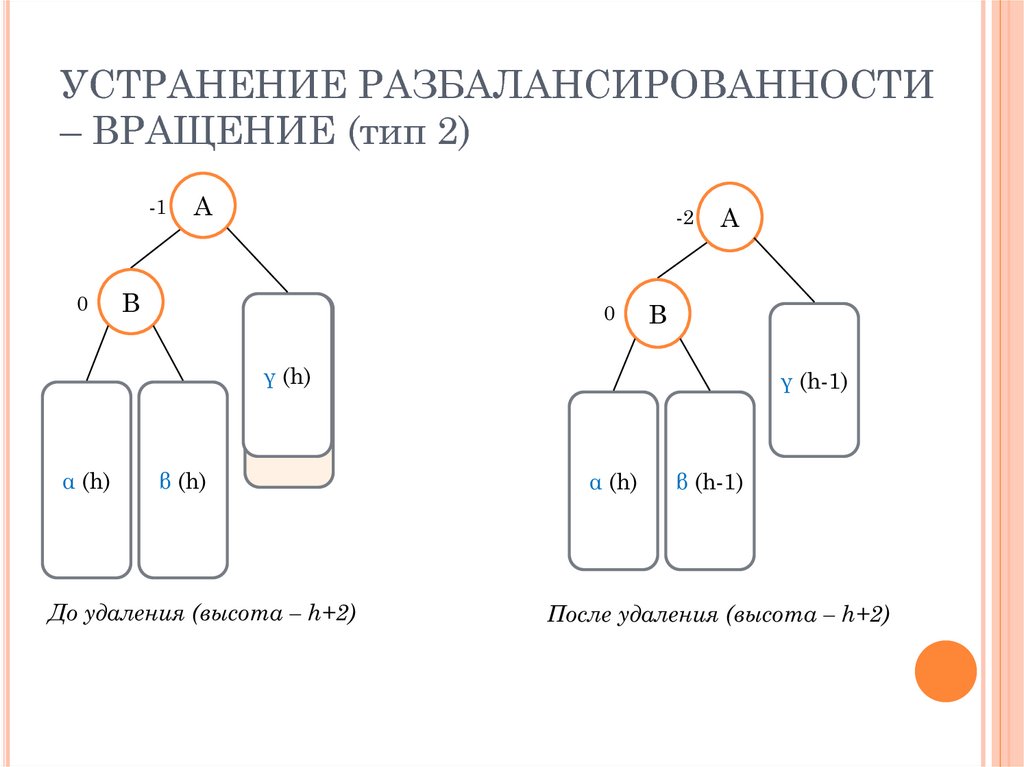
18. УСТРАНЕНИЕ РАЗБАЛАНСИРОВАННОСТИ – ВРАЩЕНИЕ (тип 2)

-1
0
A
-2
B
0
A
B
γ (h)
α (h-1)
α (h)
β (h)
До удаления (высота – h+2)
γ (h-1)
α (h)
β (h-1)
После удаления (высота – h+2)

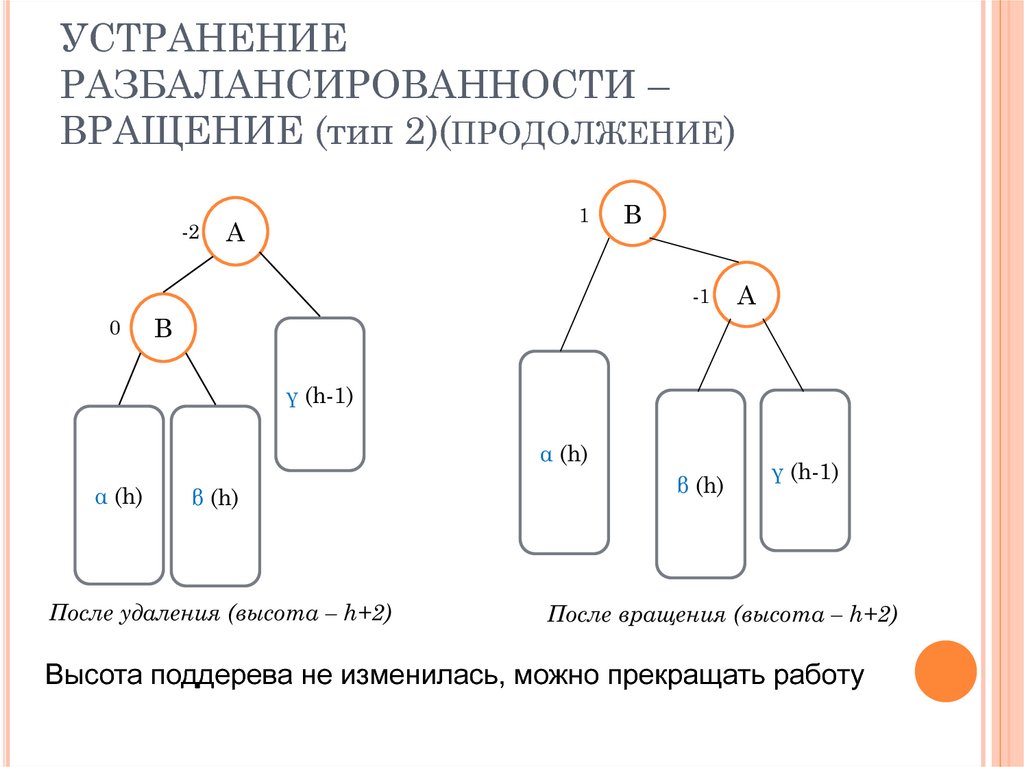
19. УСТРАНЕНИЕ РАЗБАЛАНСИРОВАННОСТИ – ВРАЩЕНИЕ (тип 2)(продолжение)

УСТРАНЕНИЕ
РАЗБАЛАНСИРОВАННОСТИ –
ВРАЩЕНИЕ (тип 2)(ПРОДОЛЖЕНИЕ)
-2
1
A
B
-1
0
A
B
γ (h-1)
α (h)
α (h)
β (h)
После удаления (высота – h+2)
β (h)
γ (h-1)
После вращения (высота – h+2)
Высота поддерева не изменилась, можно прекращать работу

20.

УСТРАНЕНИЕ
РАЗБАЛАНСИРОВАННОСТИ –
ДВОЙНОЕ ВРАЩЕНИЕ
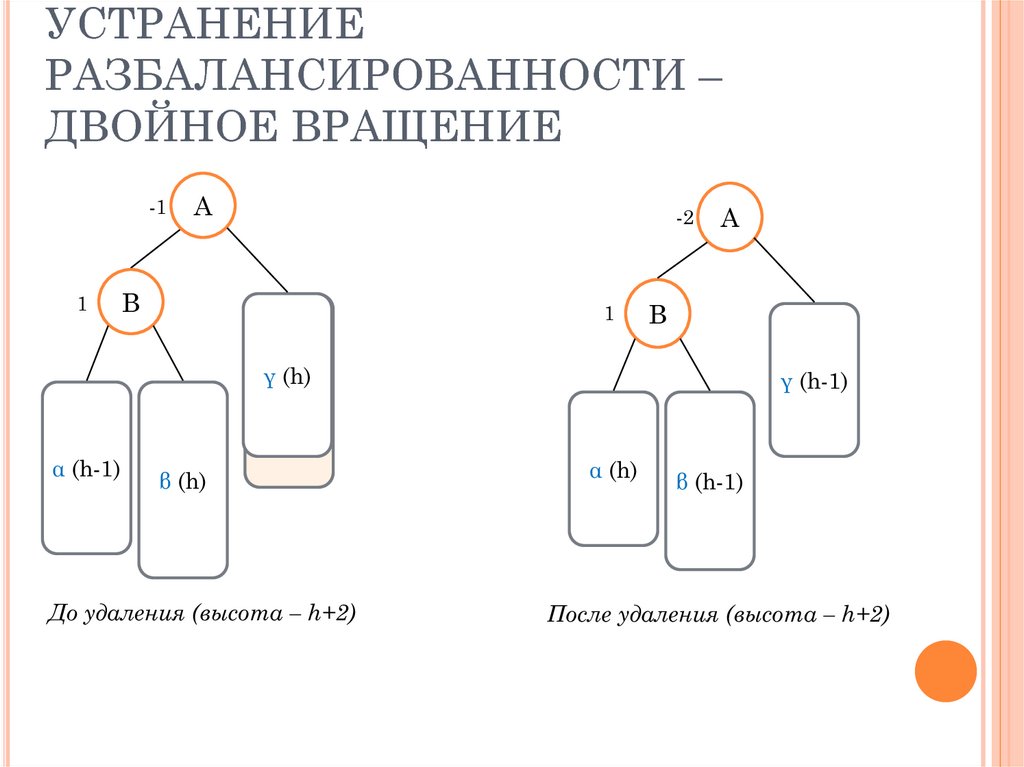
-1
1
A
-2
B
1
A
B
γ (h)
α (h-1)
α (h-1)
β (h)
До удаления (высота – h+2)
γ (h-1)
α (h)
β (h-1)
После удаления (высота – h+2)

21. Устранение разбалансированности – двойное вращение (продолжение)

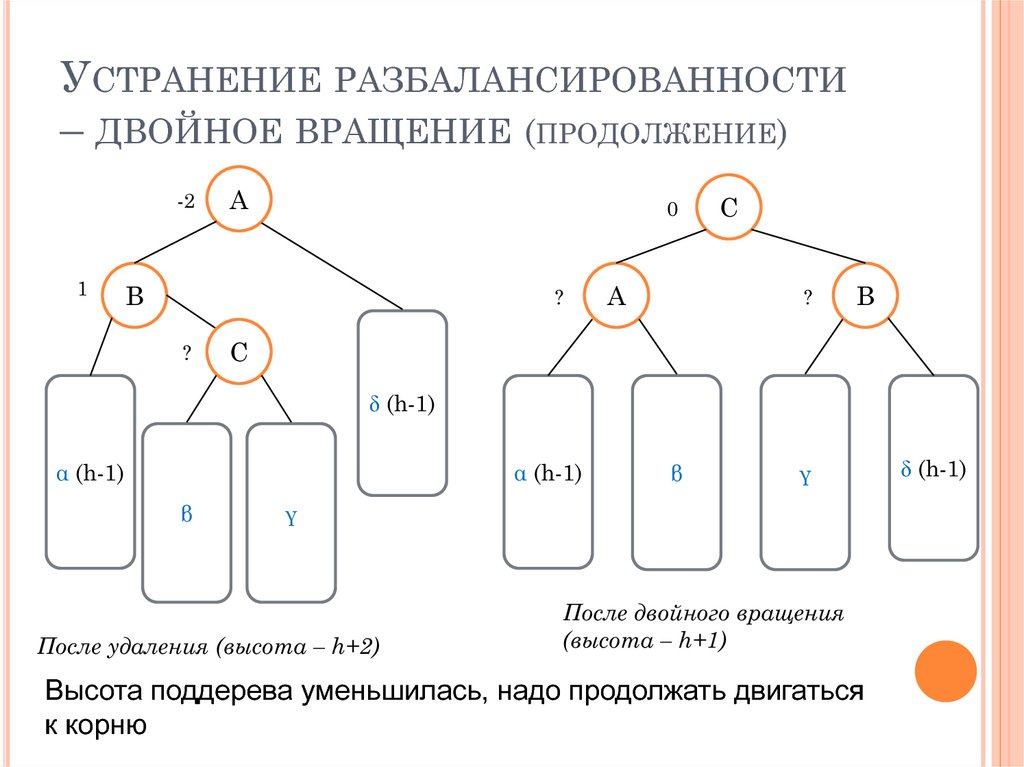
УСТРАНЕНИЕ РАЗБАЛАНСИРОВАННОСТИ
– ДВОЙНОЕ ВРАЩЕНИЕ (ПРОДОЛЖЕНИЕ)
-2
1
A
0
B
?
?
A
С
?
B
С
δ (h-1)
α (h-1)
α (h-1)
β
β
γ
γ
После удаления (высота – h+2)
После двойного вращения
(высота – h+1)
Высота поддерева уменьшилась, надо продолжать двигаться
к корню
δ (h-1)

22. СИЛЬНО ВЕТВЯЩИЕСЯ ДЕРЕВЬЯ

Сильно ветвящееся дерево ((a,b)-дерево) –
поисковое дерево, все ветви которого имеют
одинаковую высоту, а каждая вершина, кроме
листьев, имеет от a до b сыновей.
Мы будем рассматривать (2, 4)-деревья.

23. Типы вершин в (2, 4)-дереве

ТИПЫ ВЕРШИН В (2, 4)-ДЕРЕВЕ
справочные (внутренние) вершины
key[1] key[2] key[3]
son[1] son[2] son[3]
son[4]
key[i] – максимальное значение ключа в поддереве,
начинающемся с son[i];
ключи упорядочены;
количество ключей на единицу меньше количества
сыновей
информационные вершины (листья)
Info

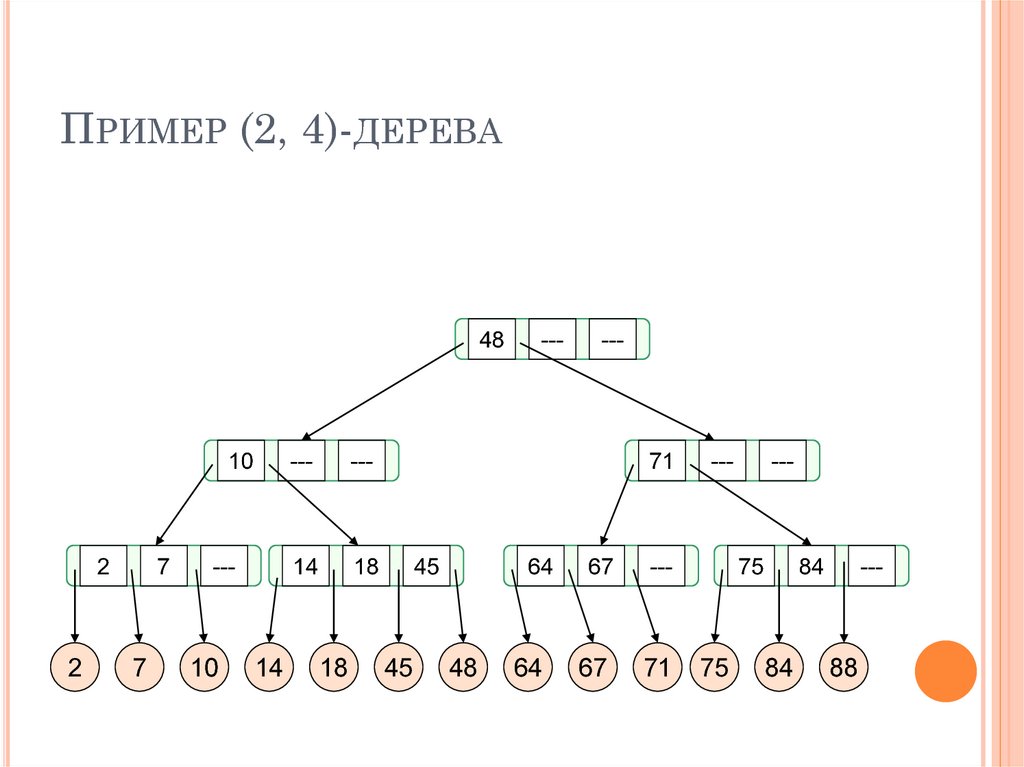
24. Пример (2, 4)-дерева

ПРИМЕР (2, 4)-ДЕРЕВА
48
10
2
2
7
7
---
10
14
---
---
14
18
18
---
---
71
45
45
64
48
64
67
---
67
71
---
---
75
75
84
84
---
88

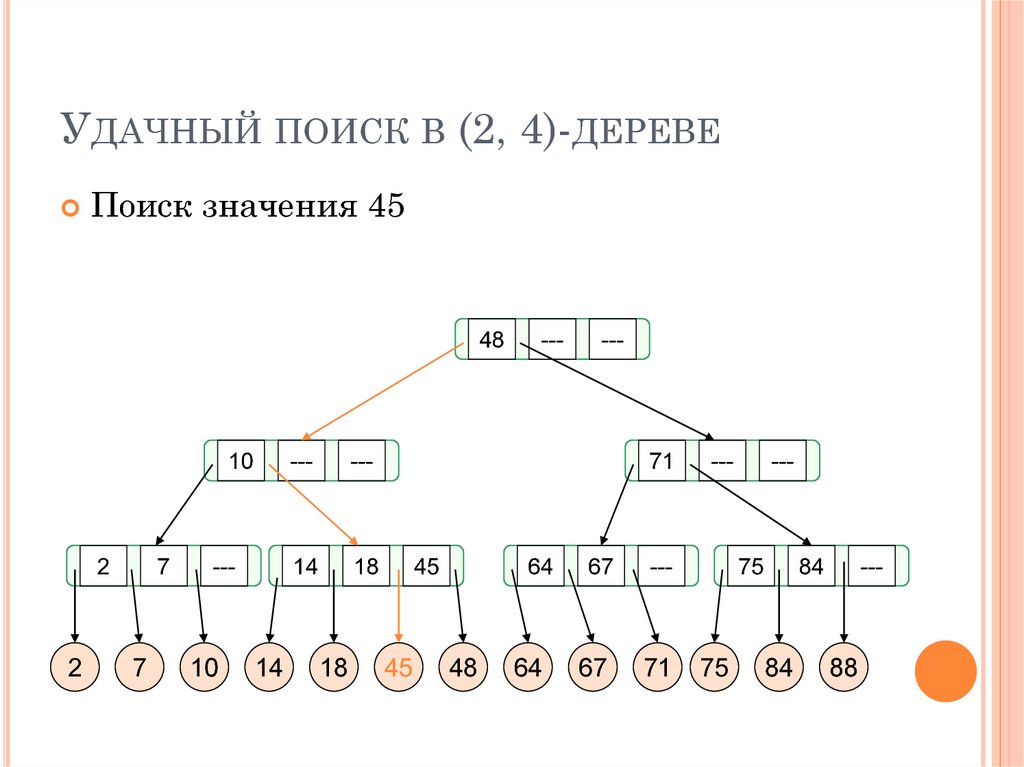
25. Удачный поиск в (2, 4)-дереве

УДАЧНЫЙ ПОИСК В (2, 4)-ДЕРЕВЕ
Поиск значения 45
48
10
2
2
7
7
---
10
14
---
---
14
18
18
---
---
71
45
45
64
48
64
67
---
67
71
---
---
75
75
84
84
---
88

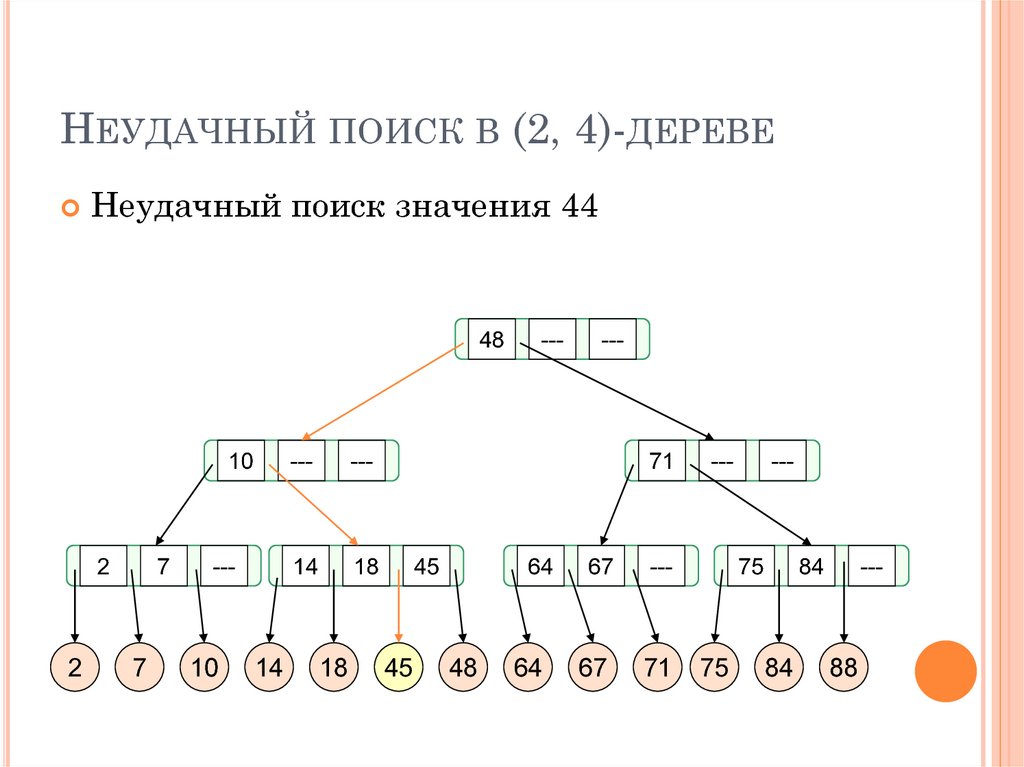
26. Неудачный поиск в (2, 4)-дереве

НЕУДАЧНЫЙ ПОИСК В (2, 4)-ДЕРЕВЕ
Неудачный поиск значения 44
48
10
2
2
7
7
---
10
14
---
---
14
18
18
---
---
71
45
45
64
48
64
67
---
67
71
---
---
75
75
84
84
---
88

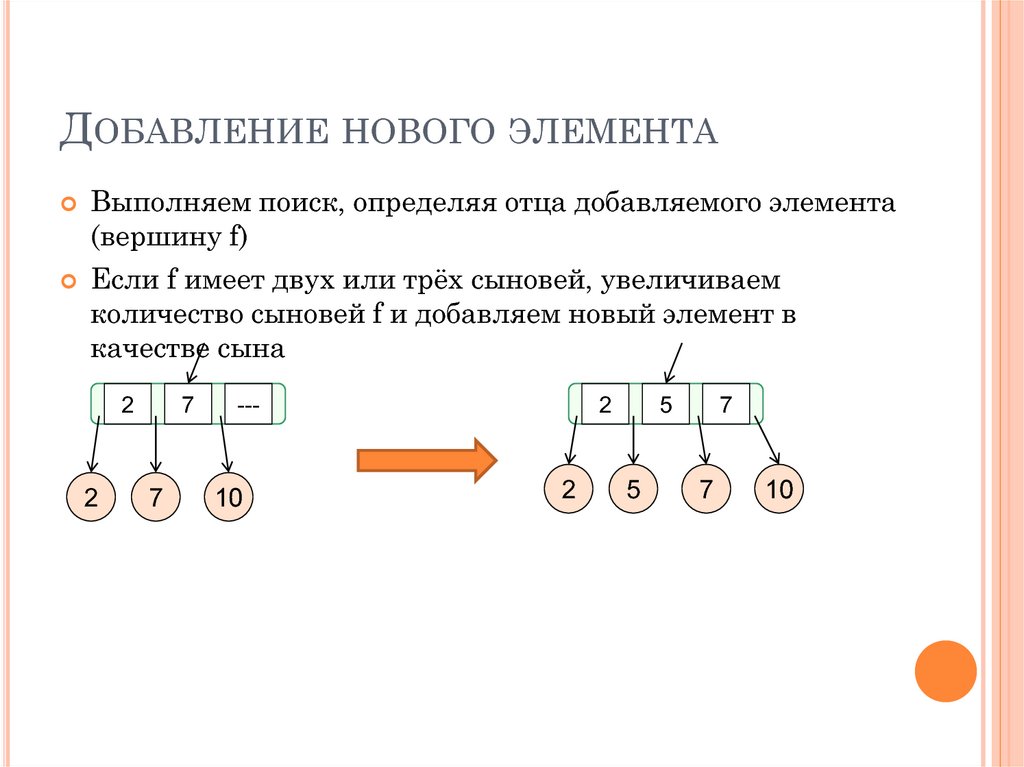
27. Добавление нового элемента

ДОБАВЛЕНИЕ НОВОГО ЭЛЕМЕНТА
Выполняем поиск, определяя отца добавляемого элемента
(вершину f)
Если f имеет двух или трёх сыновей, увеличиваем
количество сыновей f и добавляем новый элемент в
качестве сына
2
2
7
7
---
10
2
2
5
5
7
7
10

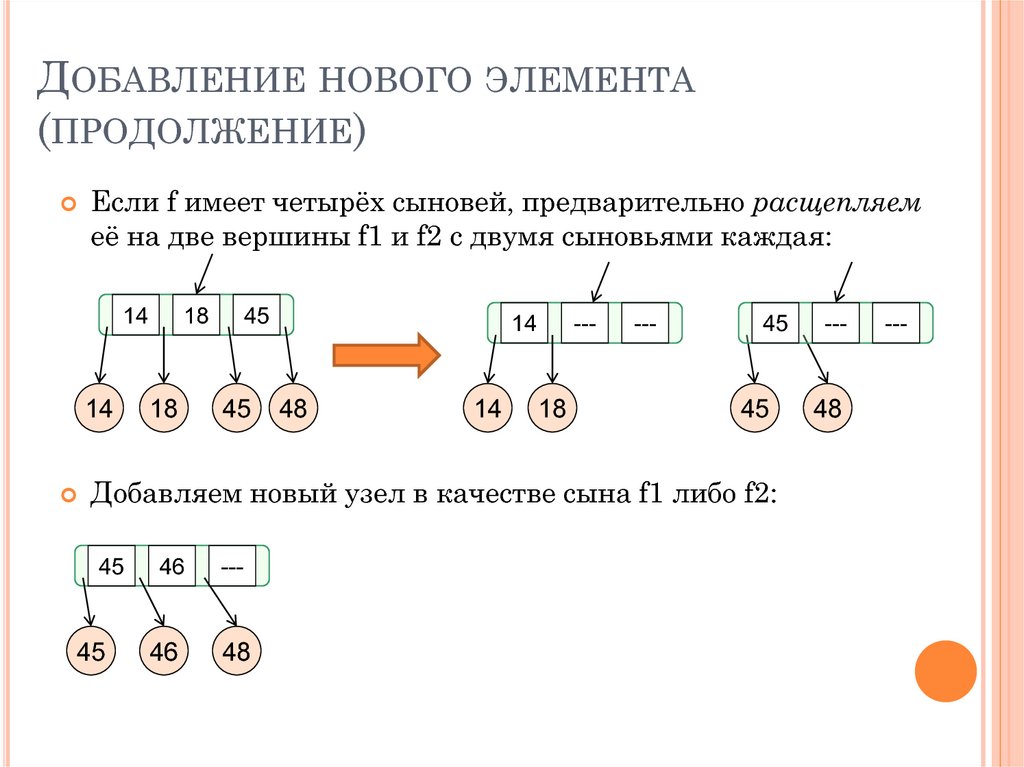
28. Добавление нового элемента (продолжение)

ДОБАВЛЕНИЕ НОВОГО ЭЛЕМЕНТА
(ПРОДОЛЖЕНИЕ)
Если f имеет четырёх сыновей, предварительно расщепляем
её на две вершины f1 и f2 с двумя сыновьями каждая:
14
14
18
18
45
45
14
48
14
---
18
---
45
45
Добавляем новый узел в качестве сына f1 либо f2:
45
45
46
46
---
48
---
48
---

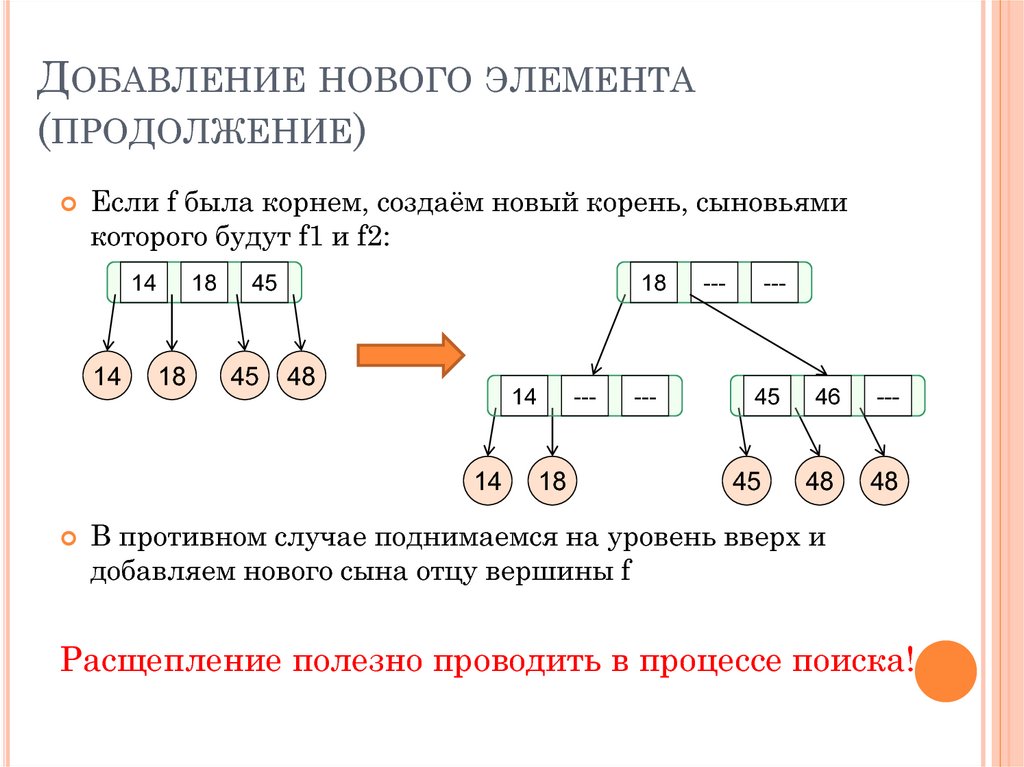
29. Добавление нового элемента (продолжение)

ДОБАВЛЕНИЕ НОВОГО ЭЛЕМЕНТА
(ПРОДОЛЖЕНИЕ)
Если f была корнем, создаём новый корень, сыновьями
которого будут f1 и f2:
14
14
18
18
45
45
18
48
14
14
---
18
---
---
---
45
45
46
---
48
48
В противном случае поднимаемся на уровень вверх и
добавляем нового сына отцу вершины f
Расщепление полезно проводить в процессе поиска!

30. Добавление нового элемента (особые случаи)

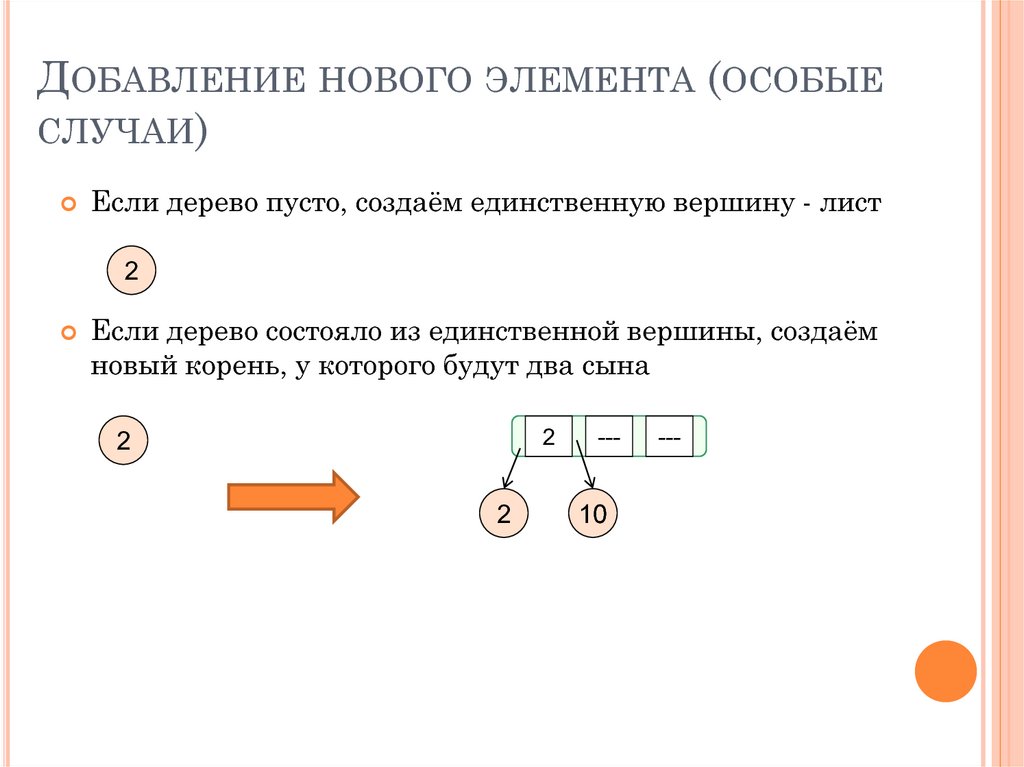
ДОБАВЛЕНИЕ НОВОГО ЭЛЕМЕНТА (ОСОБЫЕ
СЛУЧАИ)
Если дерево пусто, создаём единственную вершину - лист
2
Если дерево состояло из единственной вершины, создаём
новый корень, у которого будут два сына
2
2
2
---
10
---

31. Удаление значения из (2, 4)-дерева

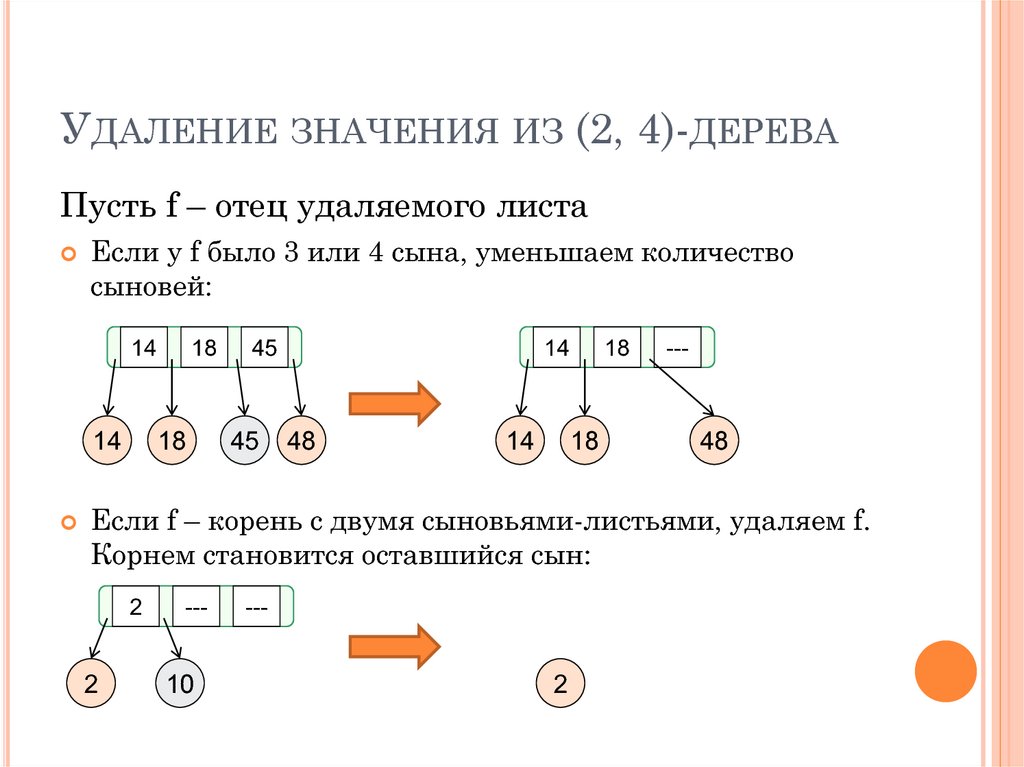
УДАЛЕНИЕ ЗНАЧЕНИЯ ИЗ (2, 4)-ДЕРЕВА
Пусть f – отец удаляемого листа
Если у f было 3 или 4 сына, уменьшаем количество
сыновей:
14
14
18
18
45
45
14
48
14
18
18
---
48
Если f – корень с двумя сыновьями-листьями, удаляем f.
Корнем становится оставшийся сын:
2
2
---
10
---
2

32. Удаление значения из (2, 4)-дерева (продолжение)

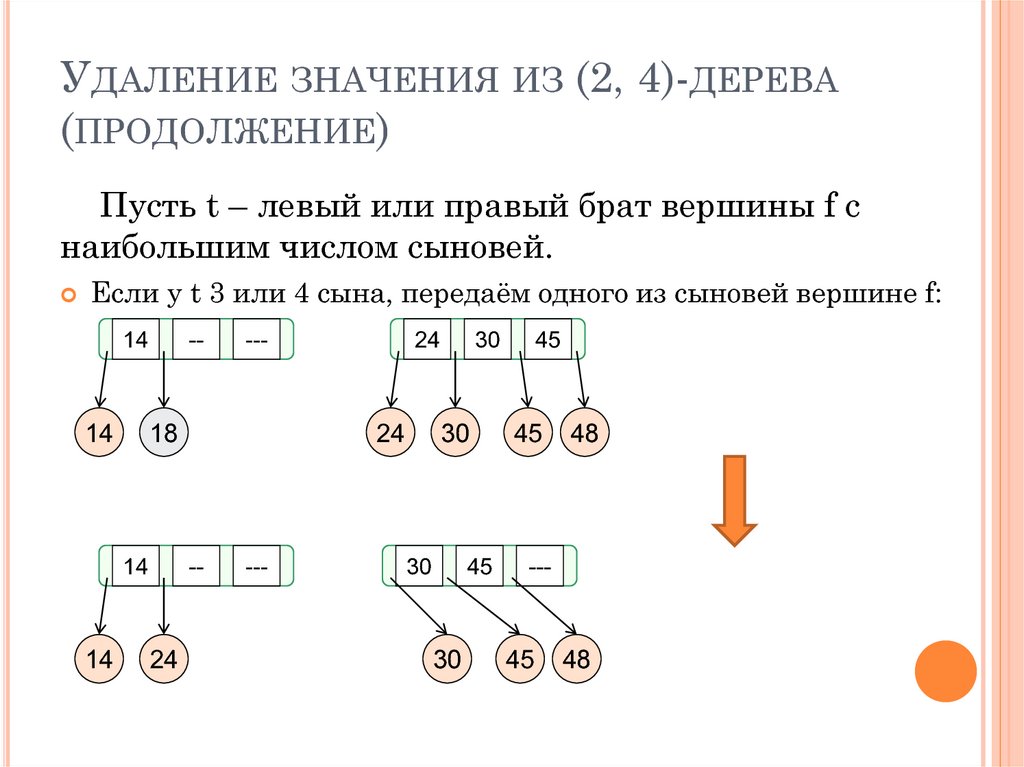
УДАЛЕНИЕ ЗНАЧЕНИЯ ИЗ (2, 4)-ДЕРЕВА
(ПРОДОЛЖЕНИЕ)
Пусть t – левый или правый брат вершины f с
наибольшим числом сыновей.
Если у t 3 или 4 сына, передаём одного из сыновей вершине f:
14
14
--
18
14
14
---
24
--
24
24
---
30
30
30
45
30
45
45
48
---
45
48

33. Удаление значения из (2, 4)-дерева (продолжение)

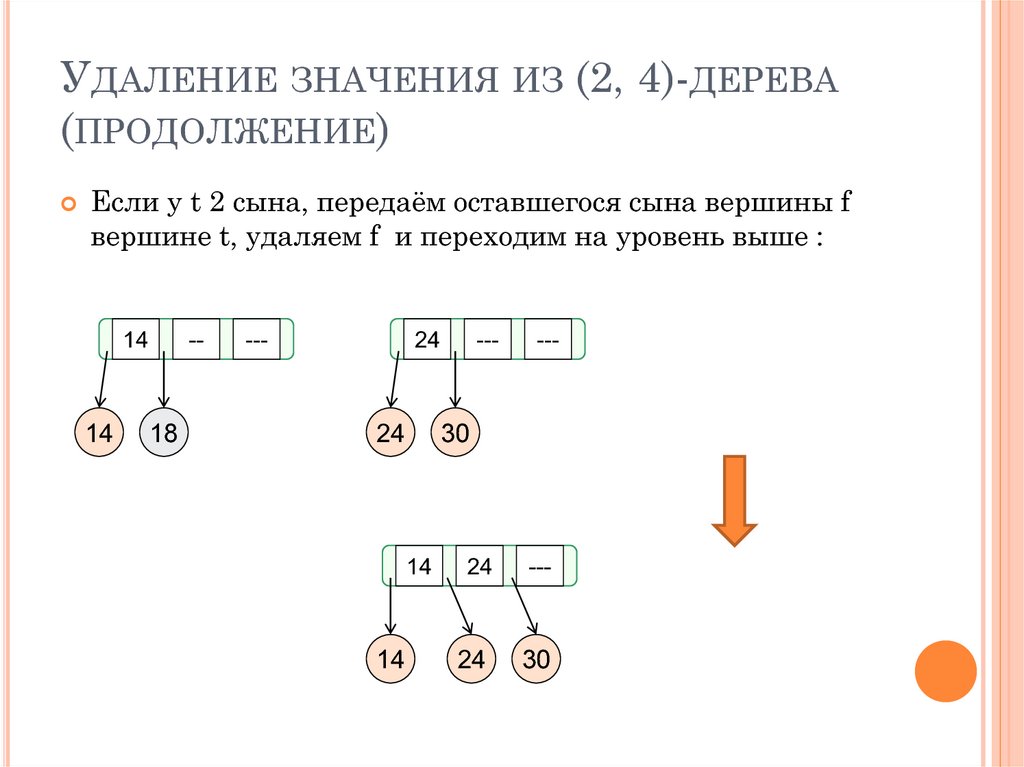
УДАЛЕНИЕ ЗНАЧЕНИЯ ИЗ (2, 4)-ДЕРЕВА
(ПРОДОЛЖЕНИЕ)
Если у t 2 сына, передаём оставшегося сына вершины f
вершине t, удаляем f и переходим на уровень выше :
14
14
--
18
---
24
24
---
30
14
14
---
24
---
24
30

34. КРАСНО-ЧЁРНЫЕ ДЕРЕВЬЯ

Красно-чёрное дерево (Red-Black-Tree, RB-Tree) — это
одно из самобалансирующихся двоичных деревьев поиска,
гарантирующих логарифмический рост высоты дерева от
числа узлов и быстро выполняющее основные операции
дерева поиска: добавление, удаление и поиск узла.

35. Свойства красно-чёрного дерева

СВОЙСТВА КРАСНО-ЧЁРНОГО ДЕРЕВА
1.
2.
3.
4.
Каждый узел покрашен либо в чёрный, либо
в красный цвет.
Листьями объявляются NIL-узлы (т.е.
"виртуальные" узлы, наследники узлов,
которые обычно называют листьями). Листья
покрашены в чёрный цвет.
Если узел красный, то оба его потомка черны.
На всех ветвях дерева, ведущих от его корня к
листьям, число черных узлов одинаково. Эта
величина называется чёрной высотой дерева.

36. Оценки высоты и количества вершин

ОЦЕНКИ ВЫСОТЫ И КОЛИЧЕСТВА
ВЕРШИН
1)
2)
3)
Если h — чёрная высота дерева, то
количество листьев не менее 2h − 1.
Если h — высота дерева, то количество
листьев не менее 2(h − 1) / 2.
Если количество листьев N, высота дерева не
больше 2log2N + 1, следовательно,
максимальная высота растёт как Θ(logN).

37. Пример чёрно-красного дерева

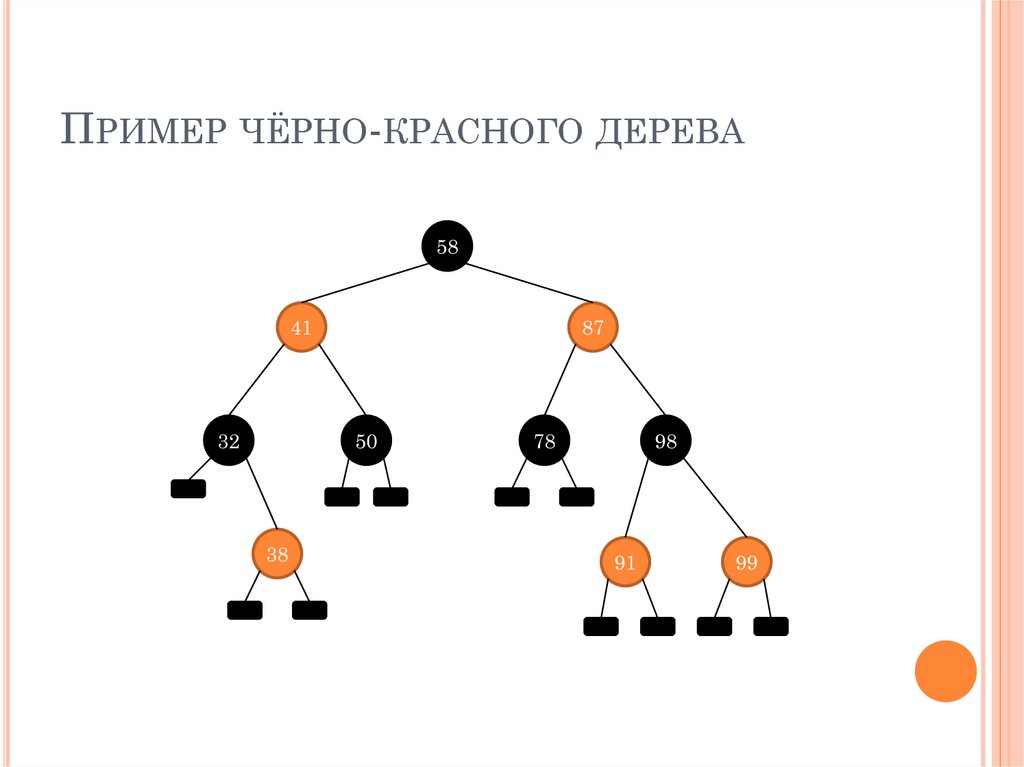
ПРИМЕР ЧЁРНО-КРАСНОГО ДЕРЕВА
58
41
32
87
50
38
78
98
91
99

38. Вставка нового элемента в красно-чёрное дерево

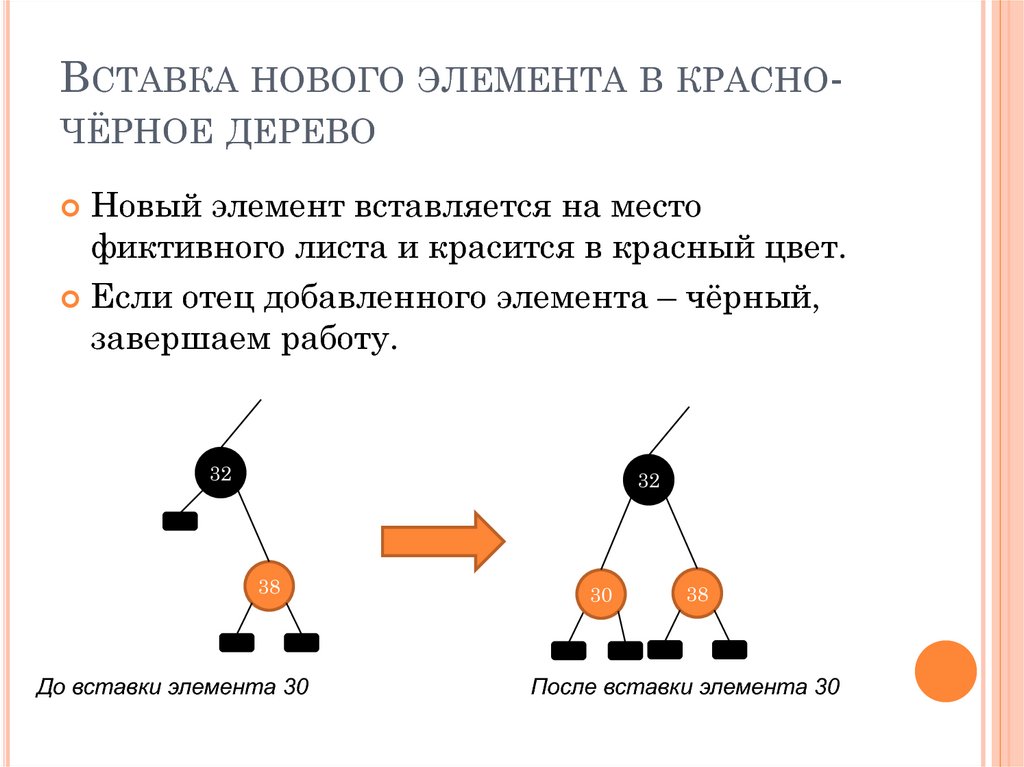
ВСТАВКА НОВОГО ЭЛЕМЕНТА В КРАСНОЧЁРНОЕ ДЕРЕВО
Новый элемент вставляется на место
фиктивного листа и красится в красный цвет.
Если отец добавленного элемента – чёрный,
завершаем работу.
32
32
38
До вставки элемента 30
30
38
После вставки элемента 30

39. Вставка нового элемента в красно-чёрное дерево (продолжение)

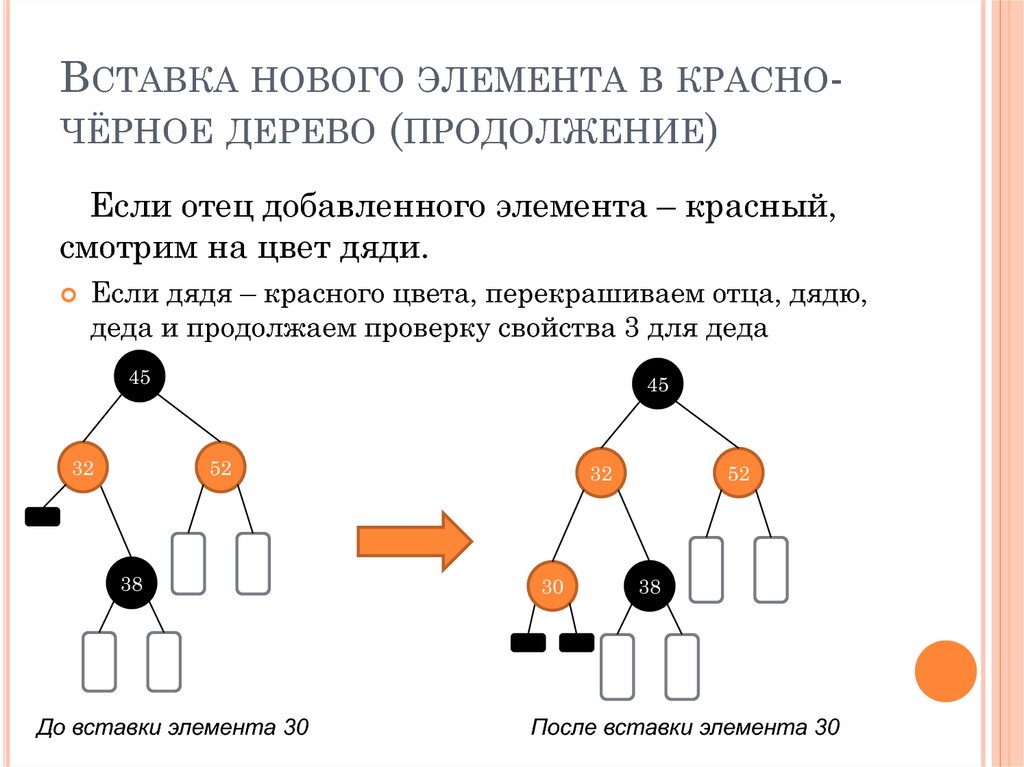
ВСТАВКА НОВОГО ЭЛЕМЕНТА В КРАСНОЧЁРНОЕ ДЕРЕВО (ПРОДОЛЖЕНИЕ)
Если отец добавленного элемента – красный,
смотрим на цвет дяди.
Если дядя – красного цвета, перекрашиваем отца, дядю,
деда и продолжаем проверку свойства 3 для деда
45
32
45
52
38
До вставки элемента 30
32
30
52
38
После вставки элемента 30

40. Вставка нового элемента в красно-чёрное дерево (продолжение)

ВСТАВКА НОВОГО ЭЛЕМЕНТА В КРАСНОЧЁРНОЕ ДЕРЕВО (ПРОДОЛЖЕНИЕ)
45
32
30
45
52
38
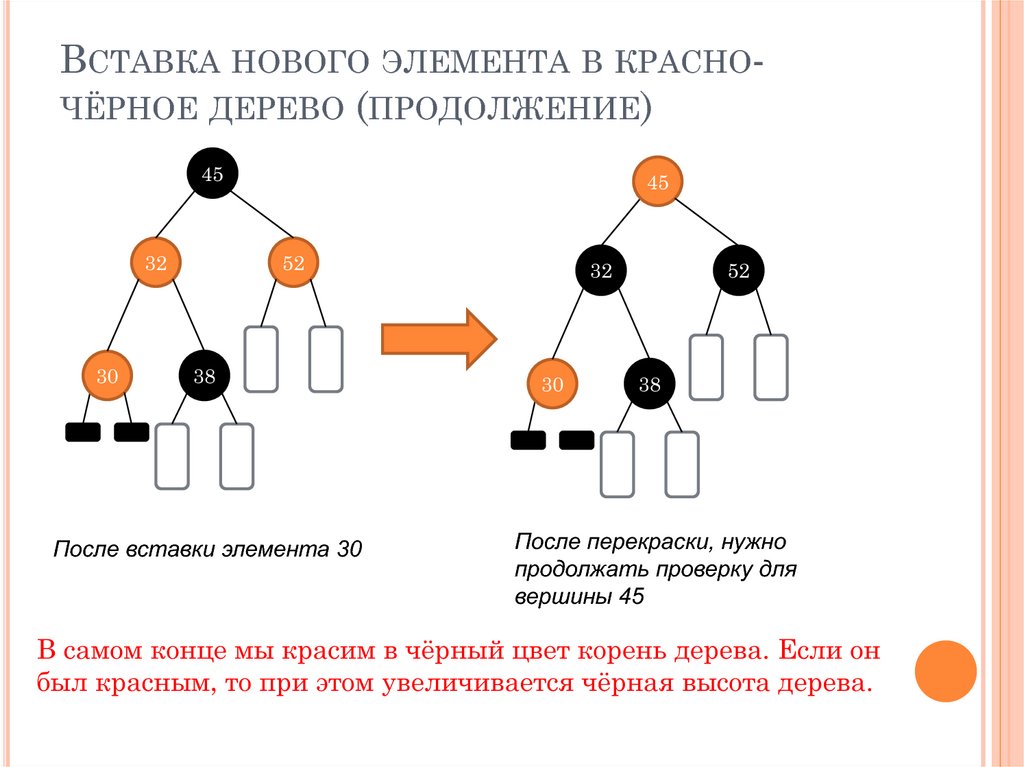
После вставки элемента 30
32
30
52
38
После перекраски, нужно
продолжать проверку для
вершины 45
В самом конце мы красим в чёрный цвет корень дерева. Если он
был красным, то при этом увеличивается чёрная высота дерева.

41. Вставка нового элемента в красно-чёрное дерево (продолжение)

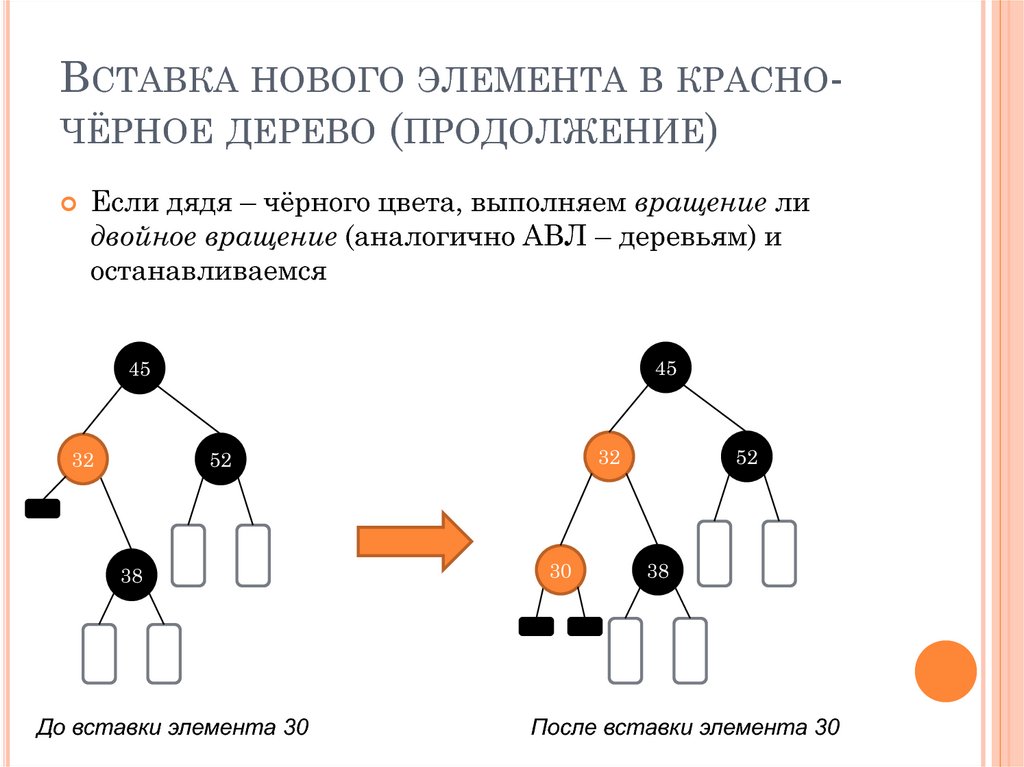
ВСТАВКА НОВОГО ЭЛЕМЕНТА В КРАСНОЧЁРНОЕ ДЕРЕВО (ПРОДОЛЖЕНИЕ)
Если дядя – чёрного цвета, выполняем вращение ли
двойное вращение (аналогично АВЛ – деревьям) и
останавливаемся
45
45
32
32
52
38
До вставки элемента 30
30
52
38
После вставки элемента 30

42. Вставка нового элемента в красно-чёрное дерево (продолжение)

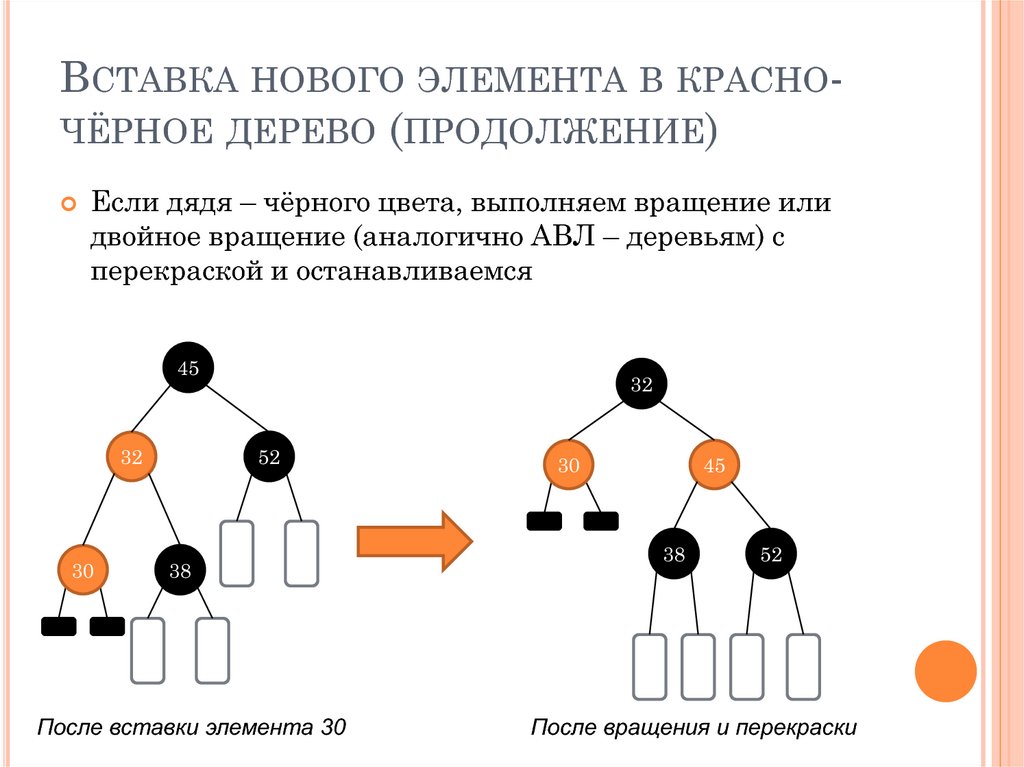
ВСТАВКА НОВОГО ЭЛЕМЕНТА В КРАСНОЧЁРНОЕ ДЕРЕВО (ПРОДОЛЖЕНИЕ)
Если дядя – чёрного цвета, выполняем вращение или
двойное вращение (аналогично АВЛ – деревьям) с
перекраской и останавливаемся
45
32
30
32
52
38
После вставки элемента 30
30
45
38
52
После вращения и перекраски

43. Удаление элемента из красно-чёрного дерева

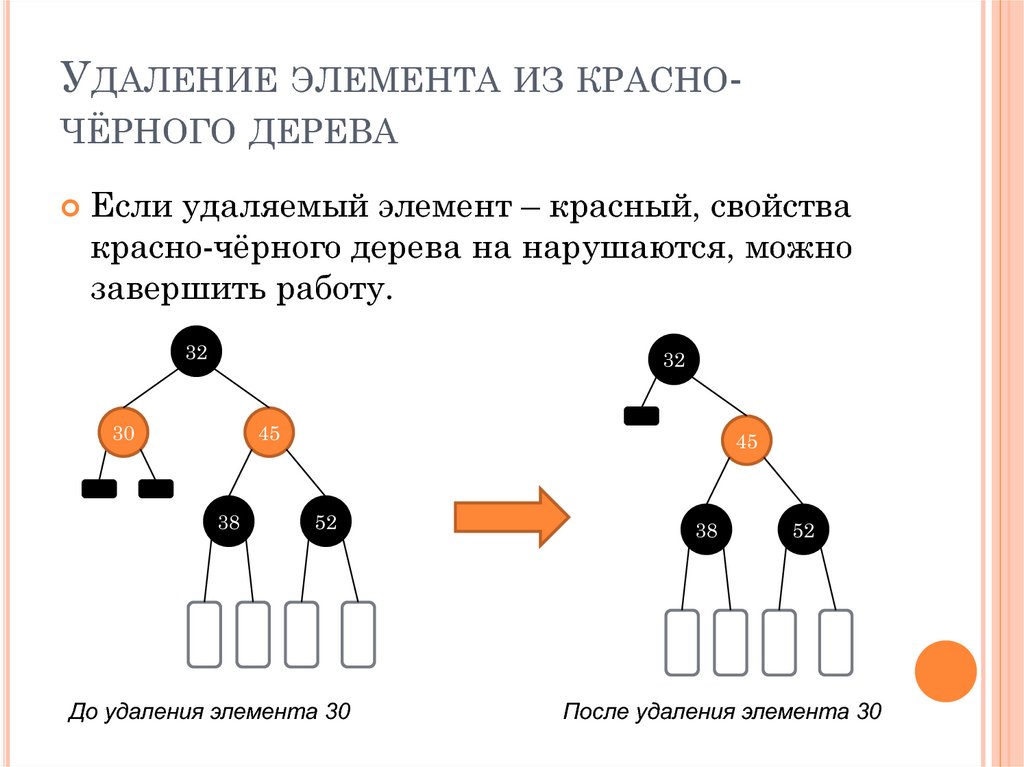
УДАЛЕНИЕ ЭЛЕМЕНТА ИЗ КРАСНОЧЁРНОГО ДЕРЕВА
Если удаляемый элемент – красный, свойства
красно-чёрного дерева на нарушаются, можно
завершить работу.
32
32
30
45
38
45
52
До удаления элемента 30
38
52
После удаления элемента 30

44. Удаление элемента из красно-чёрного дерева

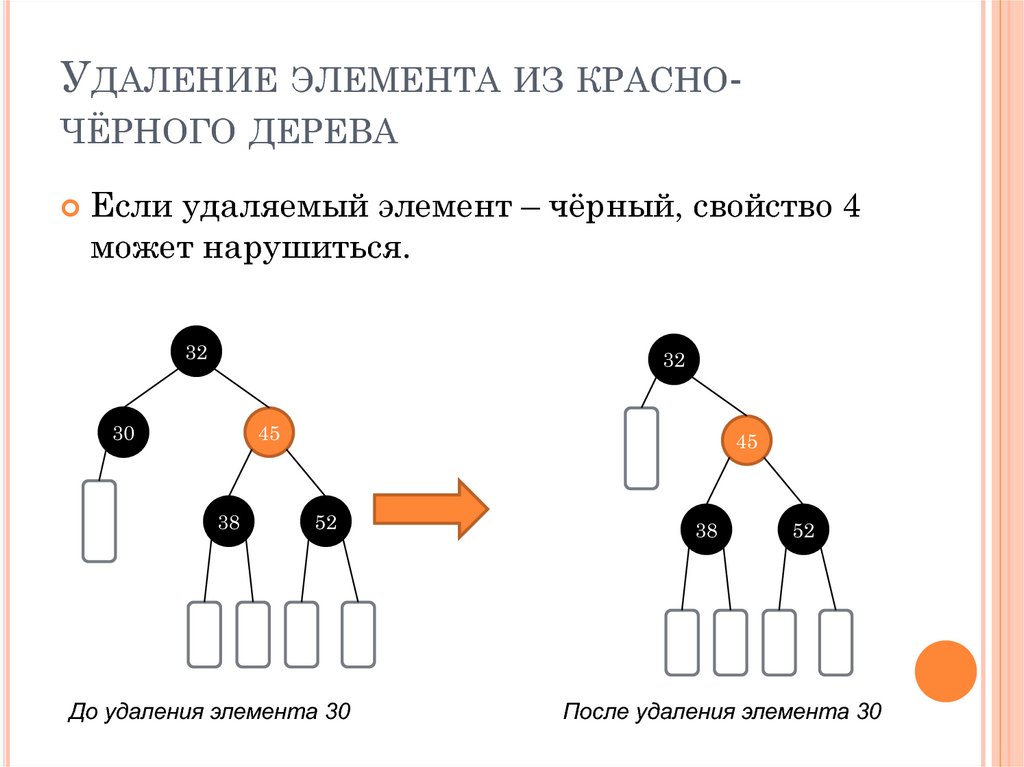
УДАЛЕНИЕ ЭЛЕМЕНТА ИЗ КРАСНОЧЁРНОГО ДЕРЕВА
Если удаляемый элемент – чёрный, свойство 4
может нарушиться.
32
32
30
45
38
45
52
До удаления элемента 30
38
52
После удаления элемента 30

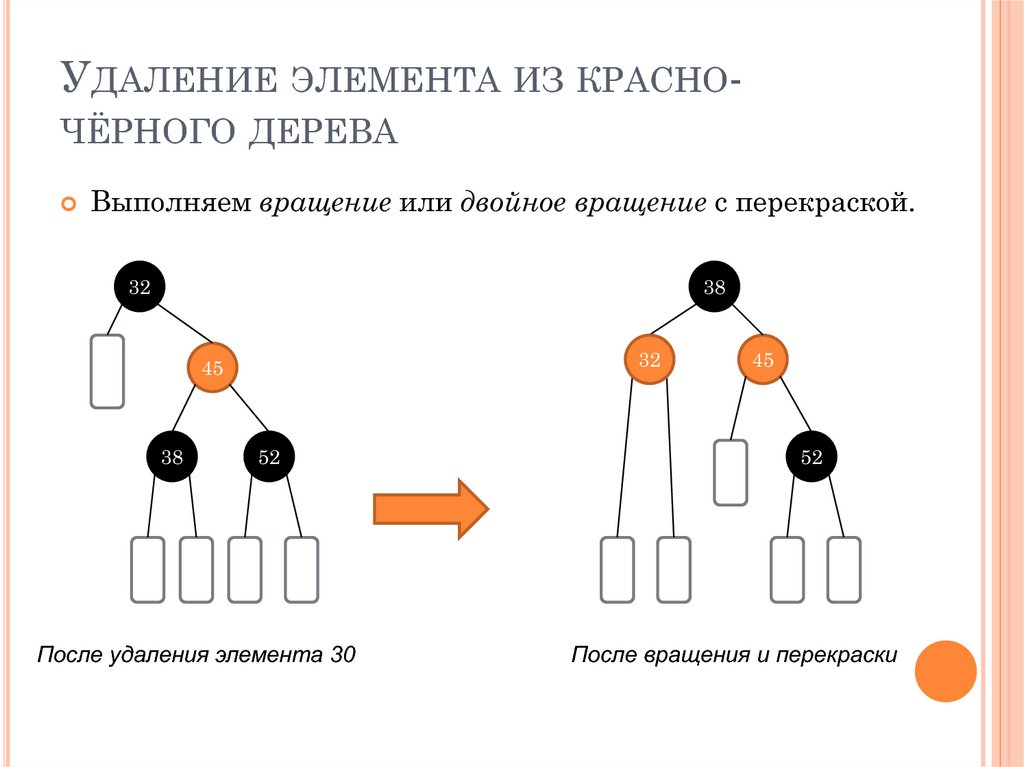
45. Удаление элемента из красно-чёрного дерева

УДАЛЕНИЕ ЭЛЕМЕНТА ИЗ КРАСНОЧЁРНОГО ДЕРЕВА
Выполняем вращение или двойное вращение с перекраской.
32
38
32
45
38
52
После удаления элемента 30
45
52
После вращения и перекраски