Фотоника. Световые волны

1. ФОТОНИКА

1
ФОТОНИКА
Лекция 2
СВЕТОВЫЕ ВОЛНЫ

2. Энергетические единицы и соотношения между ними

2
Энергетические единицы и
соотношения между ними
В оптике энергия излучения регистрируется за время
много большее, чем период колебаний электромагнитных
волн
Согласно геометрической модели, свет – это поток
лучистой энергии, распространяющийся вдоль лучей
Электромагнитное поле в однородных изотропных средах
переносит энергию E в направлении, которое указывается
оптическим лучевым вектором q
измеряется в джоулях:
E Дж

3. Поток излучения

3
Поток излучения
Поток излучения (лучистый поток) – это величина
энергии, переносимой полем в единицу времени через
данную площадку:
e
измеряется в ваттах:
e Вт
1 Вт 1
Дж
с
S
e

4. Спектральная плотность потока излучения

4
Спектральная плотность потока
излучения
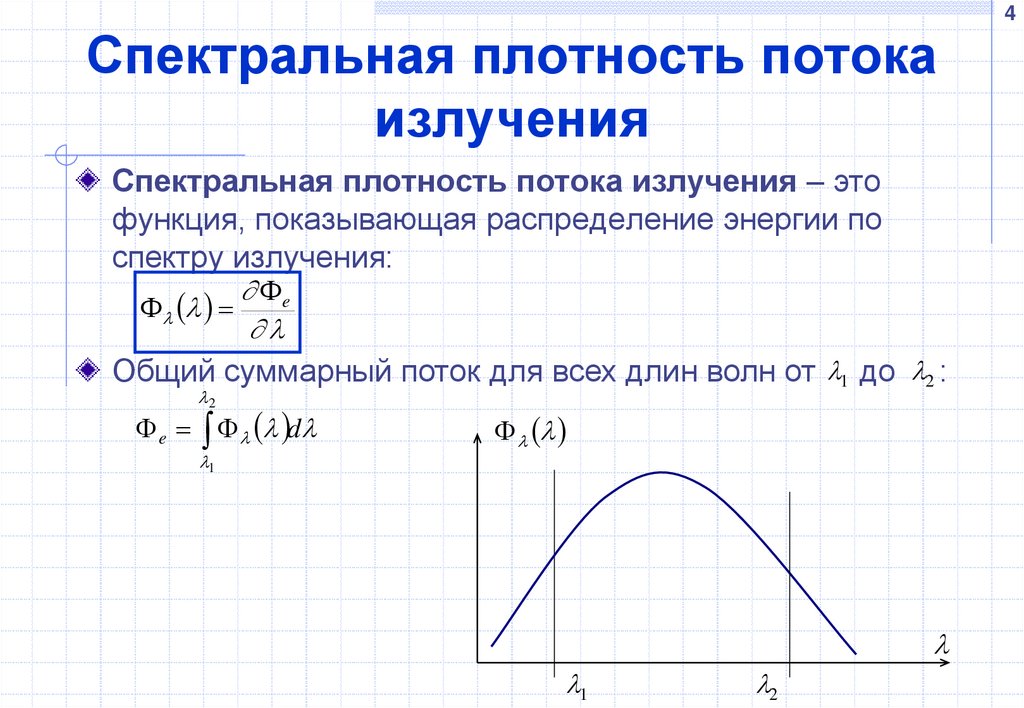
Спектральная плотность потока излучения – это
функция, показывающая распределение энергии по
спектру излучения:
e
Общий суммарный поток для всех длин волн от 1 до 2 :
2
e d
1
1
2

5. Поверхностная плотность потока энергии

5
Поверхностная плотность
потока энергии
Поверхностная плотность потока энергии – это
величина потока, приходящегося на единицу площади:
Ee
e
S
Вт
м2
если площадка освещается потоком, то поверхностная плотность потока
энергии будет иметь смысл энергетической освещенности E e
если поток излучается площадкой, то поверхностная плотность потока
энергии будет иметь смысл энергетической светимости M e
Спектральная плотность поверхностной плотности
потока показывает распределение светимости или
освещенности по спектру излучения:
Ee
Ee

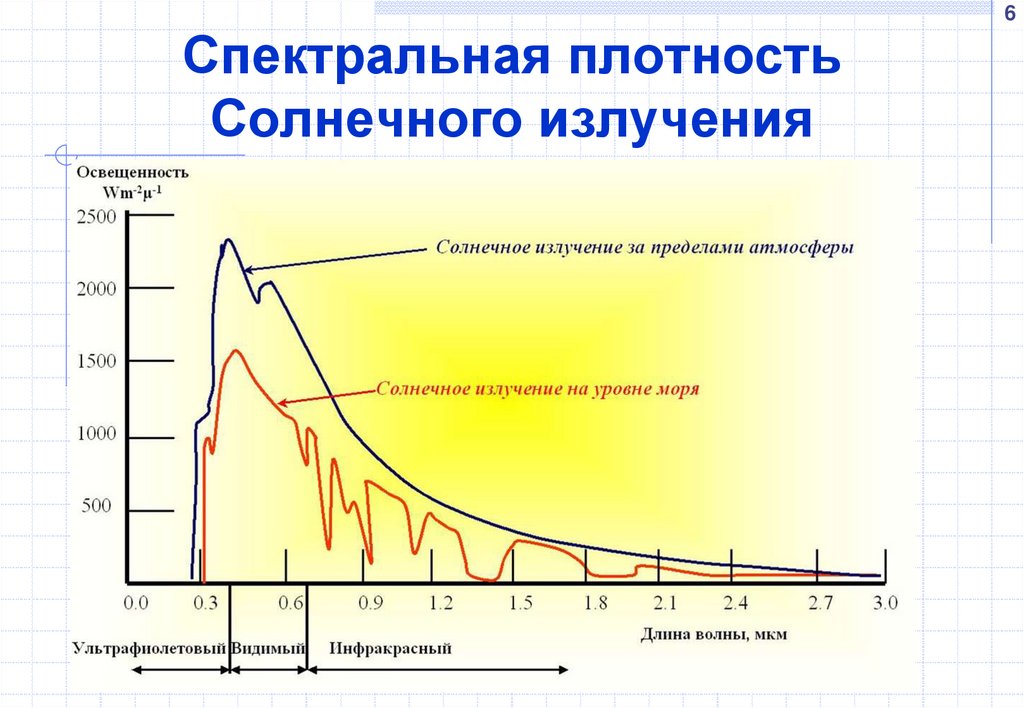
6. Спектральная плотность Солнечного излучения

6
Спектральная плотность
Солнечного излучения

7. Телесный угол

7
Телесный угол
Телесный угол данного конуса равен отношению
площади поверхности, вырезанной на сфере конусом, к
квадрату радиуса сферы:
S
r2
cp
измеряется в стерадианах
в сфере 4 ср
r
S

8. Сила излучения

8
Сила излучения
Сила излучения (энергетическая сила света) – это поток
излучения, приходящийся на единицу телесного угла, в
пределах которого он распространяется:
Ie
e
Вт
ср
за единицу энергетической силы света приняты сила излучения такого
точечного источника, у которого в пределах 1 стерадиана равномерно
распределяется поток излучения в 1 ватт
за направление силы света принимают
ось телесного угла, в пределах которого
распространяется поток излучения
r
Ie
S

9. Сила излучения

9
Сила излучения
Поток называется равномерным, если в одинаковые
телесные углы, выделенные по какому-либо
направлению, излучается одинаковый поток
Для неравномерного потока сила света определяется в
пределах элементарного телесного угла:
Ie
e
Средняя сферическая сила света:
e
Ie
4
Спектральная плотность силы излучения показывает
распределение силы излучения по спектру:
Ie
I e ( )

10. Энергетическая яркость

10
Энергетическая яркость
Энергетическая яркость – это величина потока,
излучаемого единицей площади в единицу телесного угла
в данном направлении
Если излучающая площадка dS перпендикулярна
направлению излучения:
2 e
Le
S
Вт
2
ср
м
за единицу энергетической яркости принимают яркость плоской
поверхности в 1 м2, которая в перпендикулярном направлении имеет
энергетическую силу света в 1 Вт/ср

11. Энергетическая яркость

11
Энергетическая яркость
Энергетическая яркость в общем случае:
2 e
Le
S cos
где – угол между направлением излучения и нормалью к площадке
Спектральная плотность энергетической яркости
показывает распределение энергетической яркости по
спектру:
L
Le ( ) e
dS
q
d
N

12. Инвариант яркости вдоль луча

12
Инвариант яркости вдоль луча
Яркость постоянна (инвариантна) вдоль луча при
отсутствии потерь энергии:
Le const
Если среда неоднородная, то используется приведенная
яркость (инвариант яркости):
Le
const
2
n
Следствия инварианта яркости:
яркость является основной характеристикой передачи световой энергии
оптической системой
оптическая система не может увеличивать яркость проходящего через
нее излучения

13. Поглощение света средой

13
Поглощение света средой
Энергетический коэффициент пропускания – это
отношение энергетического светового потока,
пропущенного данным телом, к энергетическому потоку,
упавшему на него:
e
e
e
0 e 1
Инвариант яркости вдоль луча для поглощающей среды:
Le
const
2
n

14. Поглощение света средой

14
Поглощение света средой
Спектральная плотность пропускания показывает
распределение коэффициента пропускания по спектру:
e ( )
Оптическая плотность среды – логарифм величины,
обратной пропусканию:
D lg
1
lg

15. Световые величины

15
Световые величины
Световые величины описывают визуальное
восприятие энергии излучения с учетом
спектрального состава света
Ф – световой поток
I – сила света
E – освещенность
M – светимость
L – яркость

16. Сила света

16
Сила света
Сила света:
I
кд
1 кандела – сила излучения эталона при температуре затвердевания
платины ( ~ 2042 K ) площадью 1/60 см2
Абсолютно черное тело – это тело, которое полностью
поглощает падающую на него энергию

17. Поток излучения и яркость

17
Поток излучения и яркость
Поток излучения:
I
лм
1 люмен – это поток, который излучается источником с силой света 1 кд в
телесном угле 1 ср:
1 лм 1 кд ср
Яркость:
L
кд
м2
за единицу яркости принята яркость такой плоской поверхности, которая в
перпендикулярном направлении излучает силу света 1 кд с 1 м2

18. Освещенность и светимость

18
Освещенность и светимость
Освещенность:
лк
E
S
1 люкс – освещенность такой поверхности, на каждый квадратный метр
которой равномерно падает поток в 1 лм
Светимость:
M лм2
м
за единицу светимости принимают светимость такой поверхности, которая
излучает с 1 м2 световой поток, равный 1 лм

19. Функция видности глаза

19
Функция видности глаза
Функция видности – это относительная спектральная
кривая эффективности монохроматического излучения
V – величина, обратно пропорциональная монохроматическим
мощностям, дающим одинаковое зрительное ощущение (воздействие
потока излучения с длиной волны 555нм принимается за единицу)

20. Спектральная чувствительность глаза

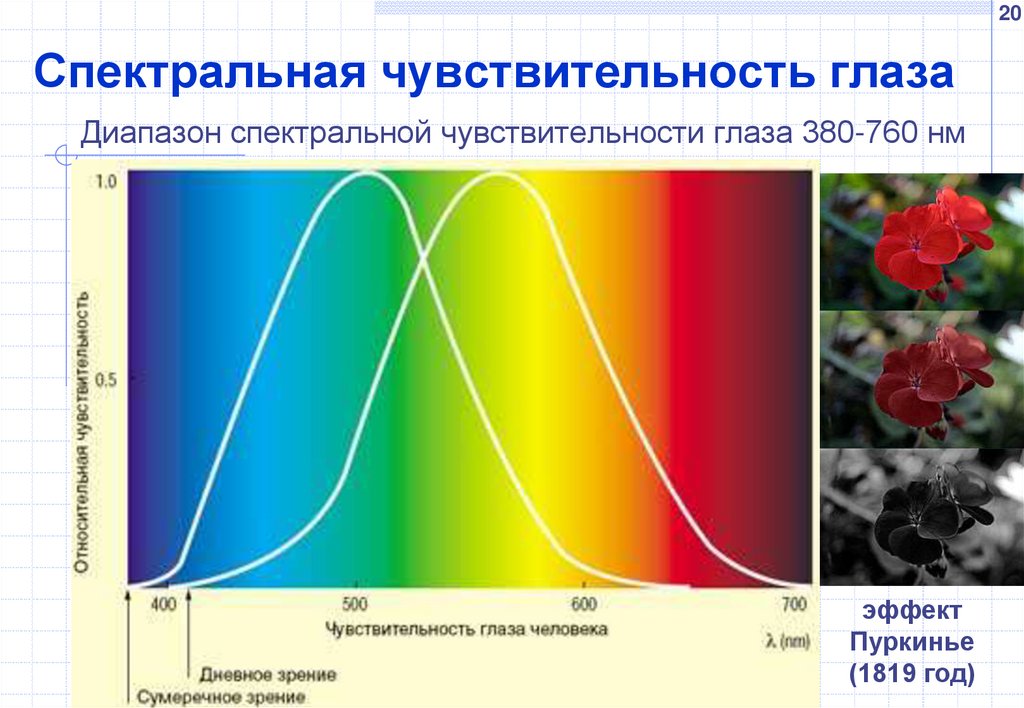
20
Спектральная чувствительность глаза
Диапазон спектральной чувствительности глаза 380-760 нм
эффект
Пуркинье
(1819 год)

21. Спектральная чувствительность некоторых приемников излучения

21
Спектральная чувствительность
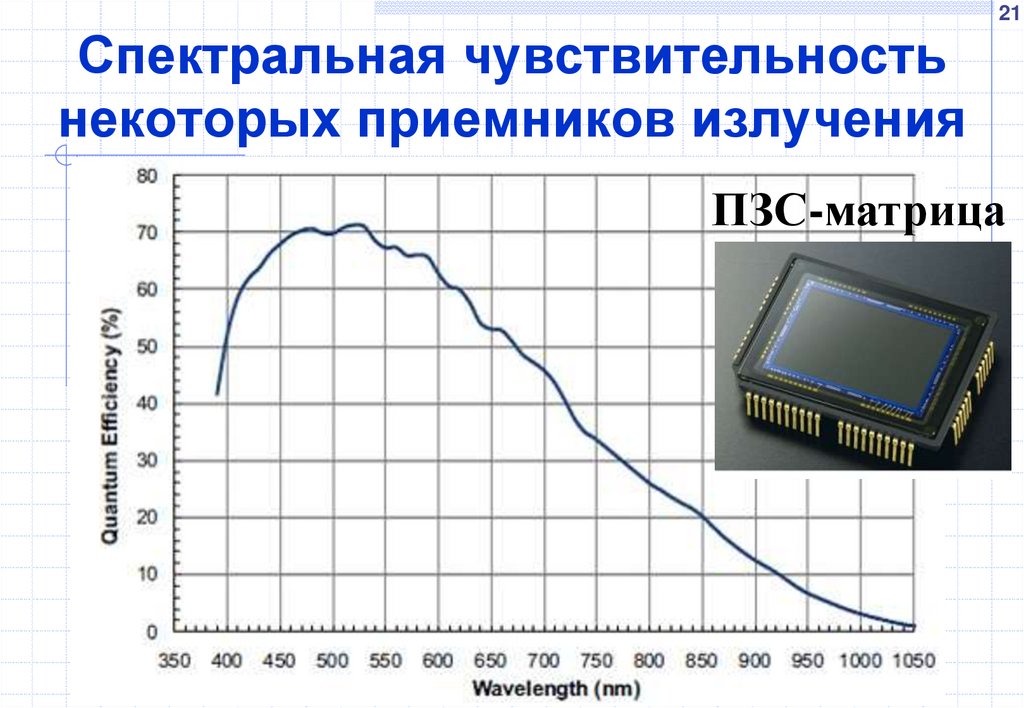
некоторых приемников излучения
ПЗС-матрица

22. Спектральная чувствительность некоторых приемников излучения

22
Спектральная чувствительность
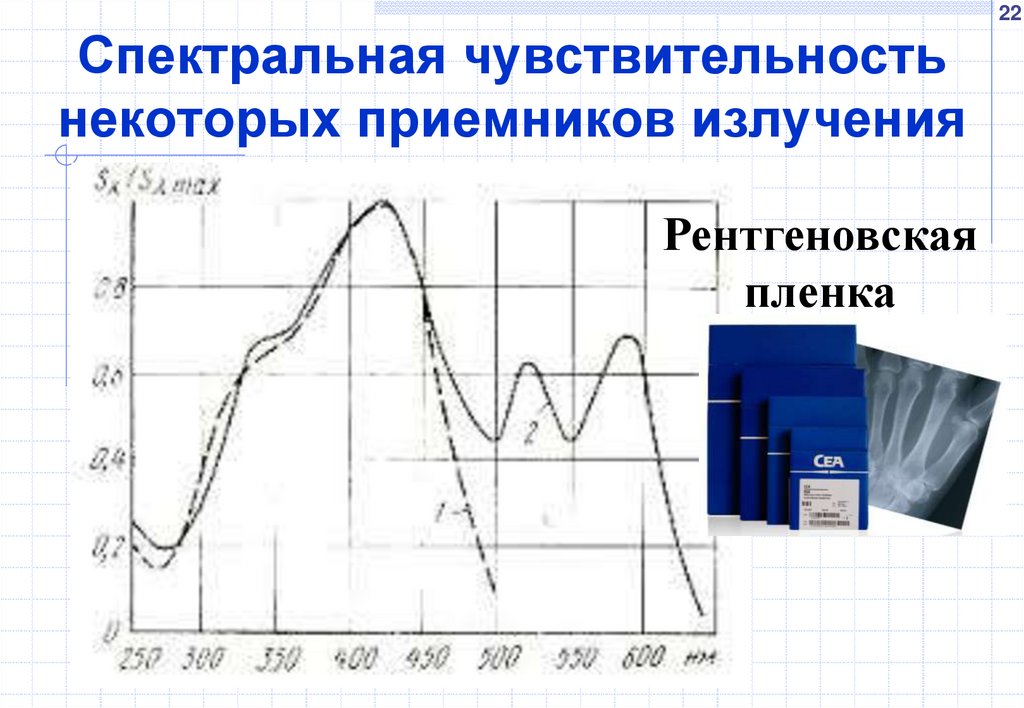
некоторых приемников излучения
Рентгеновская
пленка

23. Спектральная чувствительность некоторых приемников излучения

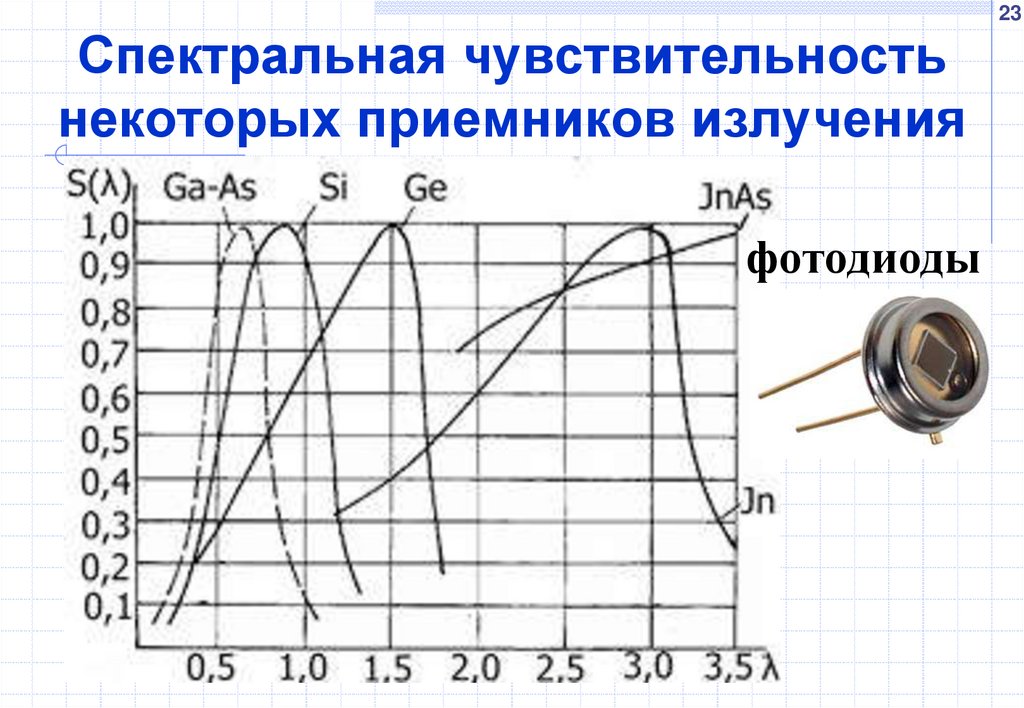
23
Спектральная чувствительность
некоторых приемников излучения
фотодиоды

24. Связь световых и энергетических величин

24
Связь световых и энергетических
величин
Определить любую световую величину Q по спектральной
плотности соответствующей энергетической величины можно
по общей формуле:
0.77
Q 680 V ( ) Qe ( ) d
0.38
где Qe ( ) – спектральная плотность соответствующей энергетической
величины, V – функция видности глаза, 680 – экспериментально
установленный коэффициент (поток излучения мощностью 1 Вт с длиной
волны 555 нм соответствует 680 лм светового потока)
0.77
например, сила света: I 680 V ( ) I e ( ) d
0.77
0.38
яркость: L 680 V ( ) Le ( ) d
0.38

25. Другие единицы измерения световых величин

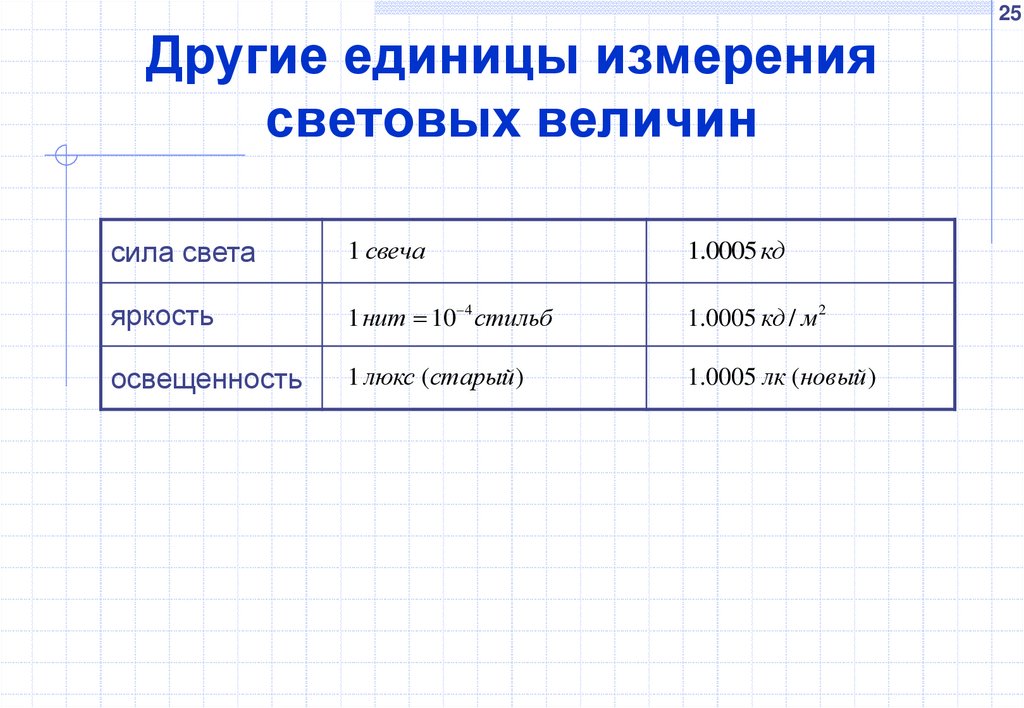
25
Другие единицы измерения
световых величин
сила света
1 свеча
1.0005 кд
яркость
1 нит 10 4 стильб
1.0005 кд / м 2
освещенность
1 люкс (старый)
1.0005 лк (новый )

26. Сопоставление энергетических и световых единиц

26
Сопоставление энергетических и
световых единиц
Энергетические
Наименование и обозначение
поток излучения e
Световые
Единицы
измерения
Вт
энергетическая освещенность E e
Вт
энергетическая светимость М e
Вт
энергетическая яркость Le
Вт
Единицы
измерения
световой поток
лм
ср
сила света I
кд
м2
освещенность E
лк
м
светимость M
лм
яркость L
кд
Вт
энергетическая сила света I e
Наименование и
обозначение
2
ср м
2
м2
м2

27. Световая экспозиция

27
Световая экспозиция
Световая экспозиция – это величина энергии,
приходящейся на единицу площади за некоторое время:
t2
H E (t ) dt
лк с
t1
Световая экспозиция при постоянной освещенности:
H E t

28. Блеск

28
Блеск
Блеск – это освещенность, создаваемая точечным
источником в плоскости зрачка наблюдателя:
EM , [ лк]
применяется при визуальном наблюдении точечного источника света
Видимый блеск небесных тел оценивается в звездных
величинах:
m 2.5 lg E M 13.89
например:
E1 1.11 10 6 лк – блеск, создаваемый звездой первой величины
E 2 1.75 10 7 лк – блеск, создаваемый звездой второй величины

29. Примеры значений световых величин

29
Примеры значений
световых величин
Яркость некоторых источников, кд/м2:
9
1.5 10 – поверхность солнца
3
2.5 10 – поверхность луны
3
1.5 10 – ясное небо
6
7
5 10 5 10 – нить лампы накаливания
4
10
– ясное безлунное ночное небо
6
– наименьшая различимая глазом яркость
10
Освещенность, лк:
5
10 – освещенность, создаваемая солнцем на поверхности Земли
(летом, днем, при безоблачном небе)
2
3
10 5 10
– освещенность рабочего места
0.2 – освещенность от полной луны
9
10
– порог блеска (примерно 8-ая звездная величина)

30. Модели источников излучения

30
Модели источников излучения
Источник излучения – это некоторая поверхность,
излучающая энергию
Характеристики источника излучения:
поток излучения
диаграмма силы света (светометрическое тело силы света) I ,
I
I
I
яркость L x, y, ,
где x, y – координаты на поверхности источника, , – углы в полярных
координатах

31. Модели источников излучения

31
Модели источников излучения
Полная модель источника определяется спектральной
плотностью энергетической яркости:
Le r, q,
z
где r x, y, z – линейный вектор,
q X ,Y , Z – угловой вектор
q
r
y
x
Ламбертовский излучатель – это такой излучатель, у
которого яркость постоянна и не зависит от направления
примеры ламбертовских излучателей: белая матовая бумага, поверхность
только что выпавшего снега

32. Плоский ламбертовский излучатель

32
Плоский ламбертовский
излучатель
Плоский ламбертовский излучатель – бесконечно
тонкий плоский диск
Сила света плоского ламбертовского источника:
I LS LS 0 cos I 0 cos
где S – проекция источника на плоскость,
перпендикулярную направлению излучения,
S0 – источник, I 0 – сила света в направлении
нормали к поверхности, – угол между
рассматриваемым направлением и нормалью
N
I0
I

33. Закон Ламберта (закон косинусов)

33
Закон Ламберта (закон косинусов)
Плоская поверхность, имеющая одинаковую яркость
по всем направлениям, излучает свет, сила которого
изменяется по закону косинуса:
I I 0 cos

34. Сферический ламбертовский излучатель

34
Сферический ламбертовский
излучатель
Сила света от сферического ламбертовского источника
постоянна во всех направлениях:
I I 0 const

35. Телесный угол в полярных координатах

35
Телесный угол в полярных
координатах
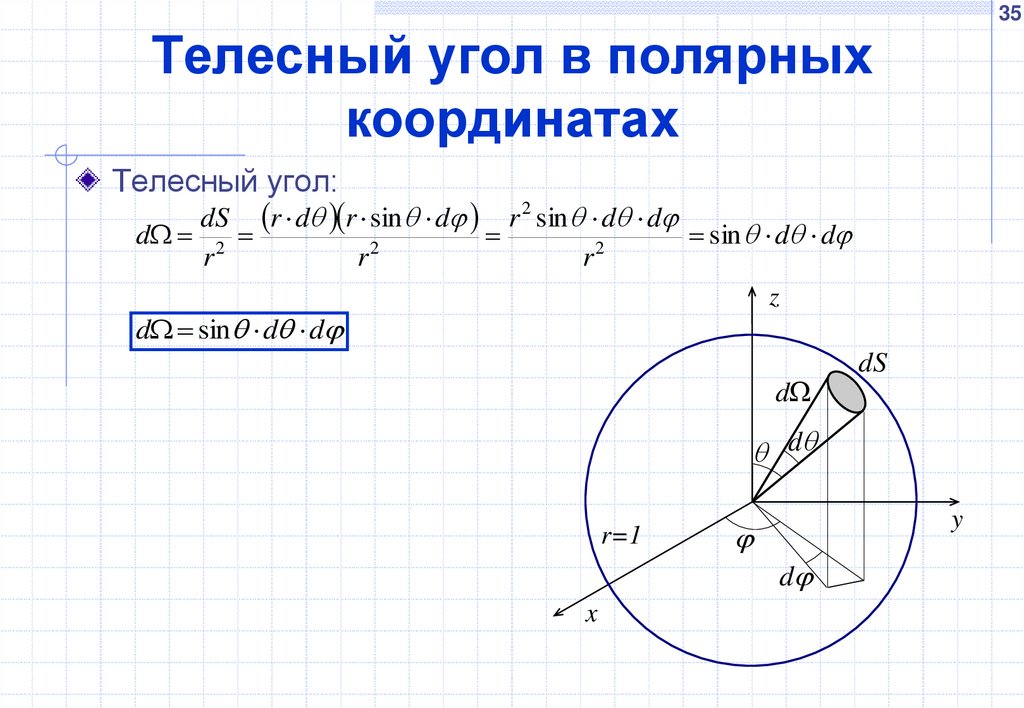
Телесный угол:
dS r d r sin d r 2 sin d d
d 2
sin d d
2
2
r
r
r
z
d sin d d
dΩ
dS
d
r=1
y
d
x

36. Поток от излучателей различной формы

36
Поток от излучателей
различной формы
Поток, проходящий через площадку:
d I d
Общий поток от произвольного излучателя в
произвольном телесном угле:
I , d I , sin d d
0
0

37. Сферический ламбертовский излучатель

37
Сферический ламбертовский
излучатель
Сила света постоянна во всех направлениях:
I ( , ) I 0 const
Поток в телесном угле 0:
I , sin d d I 0 d I 0 sin d d I 0 0
0
0
0

38. Сферический ламбертовский излучатель

38
Сферический ламбертовский
излучатель
Телесный угол, получаемый вращением плоского угла 2σ:
2
0 0
0
0 sin d d 2 sin d 2 cos 0 2 1 cos 4 sin 2
0 4 sin
2
z
2
Ω0
2
2σ
σ
y
x
Полный поток от сферического
ламбертовского излучателя в телесном угле:
I 0 0 4 I 0 sin 2
2

39. Плоский ламбертовский излучатель

39
Плоский ламбертовский
излучатель
Cила света не постоянна:
I I 0 cos
Полный поток в телесном угле, определяемым плоским
углом:
I
I 0 cos sin d d 0
2
0
I0
2
cos2 2I
0
0
2
0 0
0
sin 2 d d I 0 sin 2 d
1 cos2 I 0 sin 2
I 0 sin 2
при малых углах выражения для потока излучения сферического и
плоского источников дают одинаковый результат

40. Яркость рассеивающей поверхности

40
Яркость рассеивающей
поверхности
Ламбертовское рассеяние – рассеяние света плоской
поверхностью происходит по всем направлениям, и не
зависит от телесного угла, в пределах которого падает
световой поток
яркость поверхности постоянна по всем направлениям и не зависит от
направления падающего света
пример: белая бумага или молочное стекло
I0
I

41. Яркость рассеивающей поверхности

41
Яркость рассеивающей
поверхности
Часть падающего потока поглощается поверхностью, и
рассеивается поток:
Коэффициент альбедо определяет степень белизны
поверхности 0 1
у абсолютно черного тела 0
у абсолютно белого тела 1
0.85 0.95 – очищенный мел
0.7 0.8 – белая бумага для рисования
0.78 – свежевыпавший снег
0.25 0.3 – песок
0.01 0.002 – черный бархат

42. Яркость рассеивающей поверхности

42
Яркость рассеивающей
поверхности
Поток, упавший на рассеиватель:
E dS
Рассеянный поток в полусфере:
I 0 LdS
, следовательно:
LdS EdS
Яркость идеального рассеивателя:
E
L
где E – освещенность, создаваемая падающим потоком,
– коэффициент Альбедо

43. Освещенность, создаваемая точечным источником

43
Освещенность, создаваемая
точечным источником
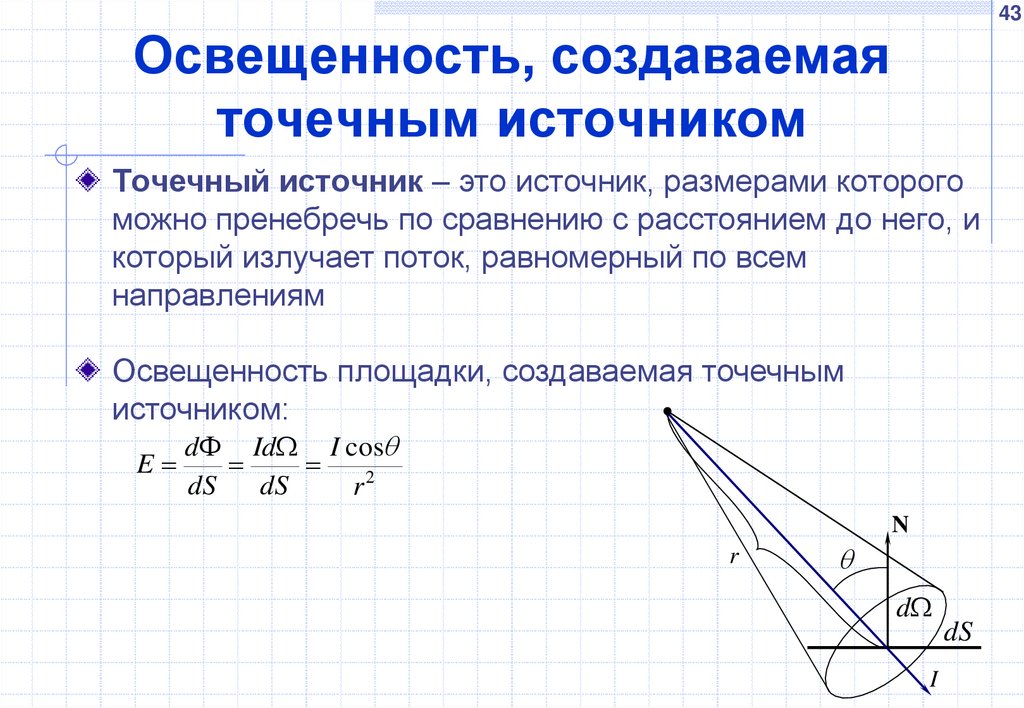
Точечный источник – это источник, размерами которого
можно пренебречь по сравнению с расстоянием до него, и
который излучает поток, равномерный по всем
направлениям
Освещенность площадки, создаваемая точечным
источником:
d Id I cos
E
dS
dS
r2
N
r
d
I
dS

44. Закон обратных квадратов

44
Закон обратных квадратов
Освещенность, создаваемая точечным источником
обратно пропорциональна расстоянию от источника до
поверхности и прямо пропорциональна косинусу угла,
между направлением светового потока и нормалью к
освещаемой поверхности:
E
I cos
r2
где I – сила света источника в направлении освещаемой точки
для соблюдения закона обратных квадратов отношение размера
источника к расстоянию до него должно быть меньше 0.1

45. Освещенность от протяженного ламбертовского источника

45
Освещенность от протяженного
ламбертовского источника
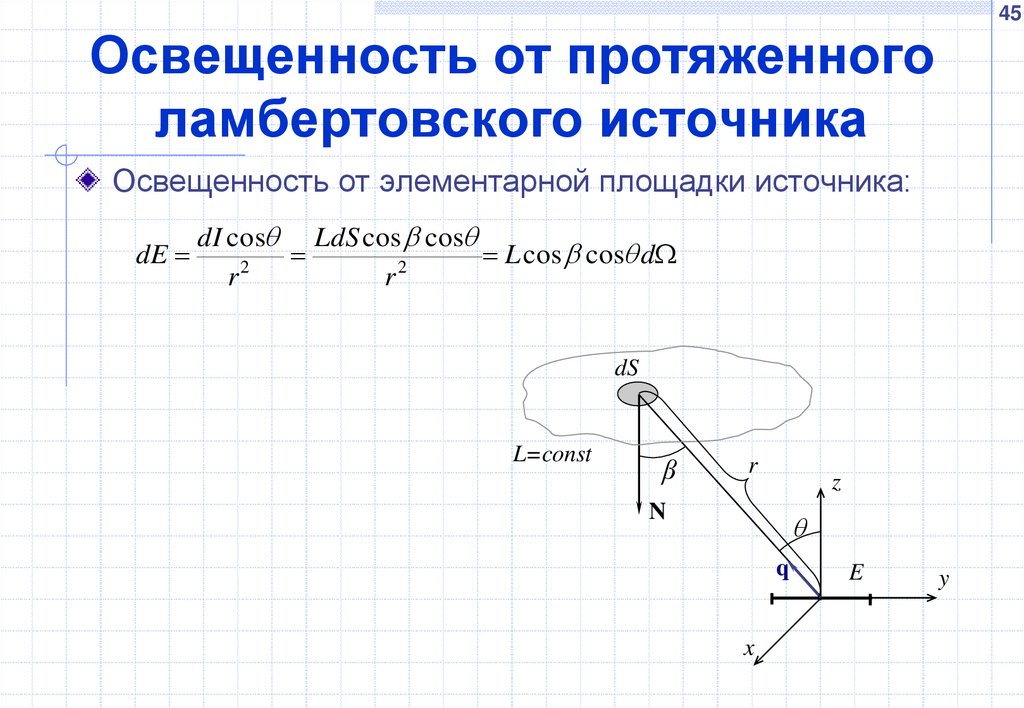
Освещенность от элементарной площадки источника:
dE
dI cos LdS cos cos
L cos cos d
2
2
r
r
dS
L=const
β
r
z
N
q
x
E
y

46. Освещенность от протяженного ламбертовского источника

46
Освещенность от протяженного
ламбертовского источника
Освещенность от всей площади источника:
E = L cos cos d
У ламбертовского источника яркость постоянна по всем
направлениям, тогда:
E L cos cos d
или
E=L dqx dq y L dXdY
где q – орт направления на источник,
q y Y cos y , qx X cos x – направляющие косинусы