Прогнозирование цен на товары или активы

1.

PREDICTION
k
True model
Pi 1 j X ji ui
j 2
k
Fitted model
Pˆi ˆ1 ˆ j X ji
j 2
В предыдущей последовательности мы увидели как прогнозировать цены на товары
или активы, учитывая их структурные характеристики.(построение). В этом ряду мы
обсудим свойства таких прогнозов.
1

2.

PREDICTION
k
True model
Pi 1 j X ji ui
j 2
k
Fitted model
Pˆi ˆ1 ˆ j X ji
j 2
Предположим, что даны примеры n наблюдений, как показано, мы установили модель
ценообразования с k-1 характеристиками.
2

3.

PREDICTION
k
True model
Pi 1 j X ji ui
j 2
k
Fitted model
Pˆi ˆ1 ˆ j X ji
j 2
k
Prediction conditional on
X
*
2
, X 3* ,..., X k*
Pˆ * ˆ1 ˆ j X *j
j 2
Предположим сейчас, что оно сталкивается с новым видом товара с
характеристиками {X2*, X3*, ..., Xk* }. Учитывая (пример) результат выборки регрессии,
естественно прогнозировать, что цена нового вида должна сводиться к третьему
уравнению.
3

4.

PREDICTION
k
True model
Pi 1 j X ji ui
j 2
k
Fitted model
Pˆi ˆ1 ˆ j X ji
j 2
k
Prediction conditional on
X
*
2
, X 3* ,..., X k*
Pˆ * ˆ1 ˆ j X *j
j 2
Что же можно сказать о свойствах этого прогнозирования? Во-первых, естественно
спросить справедливо ли оно в НЕсистематической переоценке или недооценке
смысла фактической цены. Во-вторых, мы обеспокоены о вероятной точности
прогноза
4

5.

PREDICTION
Pi 1 2 X i ui
Pˆi ˆ1 ˆ2 X i
True model
Fitted model
Prediction conditional on
X*
Pˆ * ˆ1 ˆ2 X *
Мы будем рассматривать пример, где товар имеет одну соответствующую
характеристику и предположим, что мы установили простую регрессионную
показанную модель. Следовательно, дадим новый вид товара с характеристиками X =
X * , эта модель дает нам прогнозируемую цену.
5

6.

PREDICTION
Pi 1 2 X i ui
Pˆi ˆ1 ˆ2 X i
True model
Fitted model
Prediction conditional on
Actual value of
P*
X*
Pˆ * ˆ1 ˆ2 X *
P * 1 2 X * u*
Допустим, что модель относится (обращается) к новому товару и, следовательно, к
фактической цене, условно X = X *; оно образуется как показано, где u* - это значение
нарушения условия нового товара.
6

7.

PREDICTION
Pi 1 2 X i ui
Pˆi ˆ1 ˆ2 X i
True model
Fitted model
Prediction conditional on
Actual value of
P*
X*
Pˆ * ˆ1 ˆ2 X *
P * 1 2 X * u*
PE P * Pˆ * 1 2 X * u* ˆ1 ˆ2 X *
Мы объясним ошибку прогнозирования модели PE, как разницу между ценой
фактической и прогнозируемой
7

8.

PREDICTION
Pi 1 2 X i ui
Pˆi ˆ1 ˆ2 X i
True model
Fitted model
Prediction conditional on
Actual value of
P*
X*
Pˆ * ˆ1 ˆ2 X *
P * 1 2 X * u*
PE P * Pˆ * 1 2 X * u* ˆ1 ˆ2 X *
Прогнозируемая ошибка получается путем подстановки фактической и
прогнозируемой цены.
8

9.

PREDICTION
Pi 1 2 X i ui
Pˆi ˆ1 ˆ2 X i
True model
Fitted model
Prediction conditional on
Actual value of
X*
P*
Pˆ * ˆ1 ˆ2 X *
P * 1 2 X * u*
PE P * Pˆ * 1 2 X * u* ˆ1 ˆ2 X *
E u E ˆ X E ˆ
E PE E 1 2 X * u* E ˆ1 ˆ2 X *
1 2 X *
*
*
1
2
1 2 X * 1 X * 2 0
Мы ожидаем.
9

10.

PREDICTION
Pi 1 2 X i ui
Pˆi ˆ1 ˆ2 X i
True model
Fitted model
Prediction conditional on
Actual value of
X*
P*
Pˆ * ˆ1 ˆ2 X *
P * 1 2 X * u*
PE P * Pˆ * 1 2 X * u* ˆ1 ˆ2 X *
E u E ˆ X E ˆ
E PE E 1 2 X * u* E ˆ1 ˆ2 X *
1 2 X *
*
*
1
2
1 2 X * 1 X * 2 0
β1 и β2 приняты с фиксированными параметрами, поэтому ожидания на них не
влияют. Также X * принято считать фиксированной величиной и также ожидания
не воздействуют. Тем не менее, u* ˆ1 и ˆ 2 случайные переменные.
10

11.

PREDICTION
Pi 1 2 X i ui
Pˆi ˆ1 ˆ2 X i
True model
Fitted model
Prediction conditional on
Actual value of
X*
P*
Pˆ * ˆ1 ˆ2 X *
P * 1 2 X * u*
PE P * Pˆ * 1 2 X * u* ˆ1 ˆ2 X *
E u E ˆ X E ˆ
E PE E 1 2 X * u* E ˆ1 ˆ2 X *
1 2 X *
*
*
1
2
1 2 X * 1 X * 2 0
E(u*) = 0 потому что u* выявлено случайно из распределения для u, который мы
приняли как нулевую совокупность. В соответствии с обычными
предположениями МНК ˆ1 есть несмещенная оценка β1 и ˆ2 является несмещенной
оценкой ˆ2
11

12.

PREDICTION
Pi 1 2 X i ui
Pˆi ˆ1 ˆ2 X i
True model
Fitted model
Prediction conditional on
Actual value of
X*
P*
Pˆ * ˆ1 ˆ2 X *
P * 1 2 X * u*
PE P * Pˆ * 1 2 X * u* ˆ1 ˆ2 X *
E u E ˆ X E ˆ
E PE E 1 2 X * u* E ˆ1 ˆ2 X *
1 2 X *
*
*
1
2
1 2 X * 1 X * 2 0
Следовательно, ожидание ошибки прогнозирования равен нулю. Результат легко
обобщается в случае, где множественные характеристики и новые товары включают в
себя новую комбинацию
12

13.

PREDICTION
Variance of prediction error
2
PE
2
*
1
X X 2
1 n
u
n X i X 2
i 1
Показана дисперсия совокупности ошибки прогнозирования. Неудивительно, что это
подразумевает, далее - значение X * от среднего значения выборки, что дисперсия
совокупности ошибки прогнозирования будет больше.
13

14.

PREDICTION
Variance of prediction error
2
PE
2
*
1
X X 2
1 n
u
n X i X 2
i 1
Также подразумевается, что снова неудивительно, что тем больше образец, тем меньше
будет дисперсия совокупности ошибки прогнозирования с нижним лимитом σu2
14

15.

PREDICTION
Variance of prediction error
2
PE
2
*
1
X X 2
1 n
u
n X i X 2
i 1
При условии, что допущения модели регрессии действительны, ˆ1 и ˆ2 будут
стремиться к их реальным значениям, так как образец становится больше, поэтому
единственным источником ошибки в прогнозировании будет u*, и по определению оно
имеет дисперсию совокупности σu2.
15

16.

PREDICTION
Variance of prediction error
2
PE
2
*
1
X X 2
1 n
u
n X i X 2
i 1
Standard error
2
1
X * X 2
s.e. PE 1 n
ˆ u
n X i X 2
i 1
Стандартная ошибка прогнозирования вычисляется используя квадратный корень
выражения для дисперсии совокупности, заменяя дисперсию u с оценкой, полученной
при подгонке модели в период выборки.
16

17.

PREDICTION
P
Pˆ * t crit s.e. P * Pˆ * t crit s.e.
upper limit of confidence interval for P*
Pˆ ˆ1 ˆ2 X
0
50
100
X
150
X*
200
X250
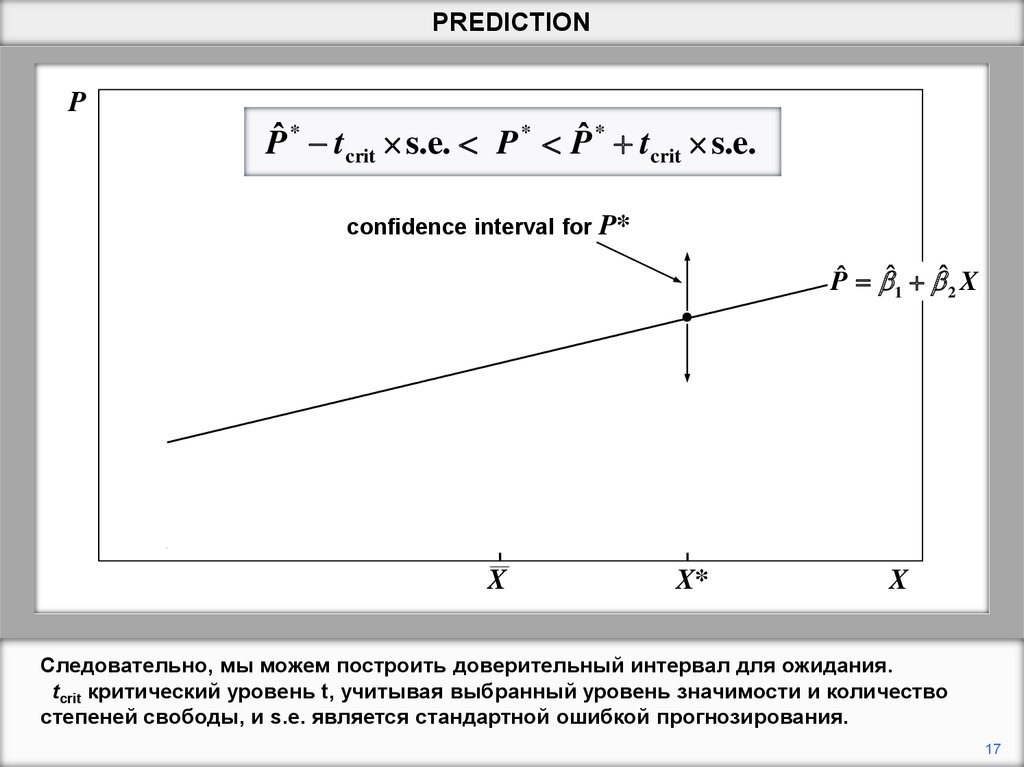
Следовательно, мы можем построить доверительный интервал для ожидания.
tcrit критический уровень t, учитывая выбранный уровень значимости и количество
степеней свободы, и s.e. является стандартной ошибкой прогнозирования.
17

18.

PREDICTION
P
Pˆ * t crit s.e. P * Pˆ * t crit s.e.
upper limit of confidence interval for P*
Pˆ ˆ1 ˆ2 X
lower limit of confidence
interval for P*
0
50
100
X
150
X*
200
X250
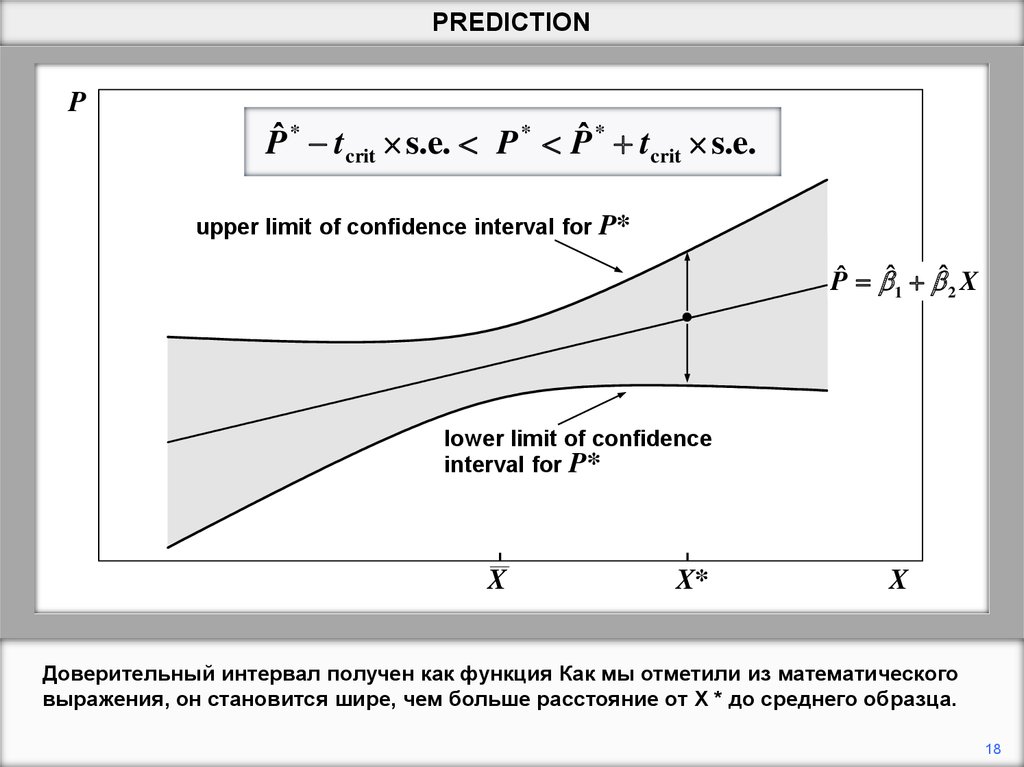
Доверительный интервал получен как функция Как мы отметили из математического
выражения, он становится шире, чем больше расстояние от X * до среднего образца.
18

19.

PREDICTION
P
Pˆ * t crit s.e. P * Pˆ * t crit s.e.
upper limit of confidence interval for P*
Pˆ ˆ1 ˆ2 X
lower limit of confidence
interval for P*
0
50
100
X
150
X*
200
X250
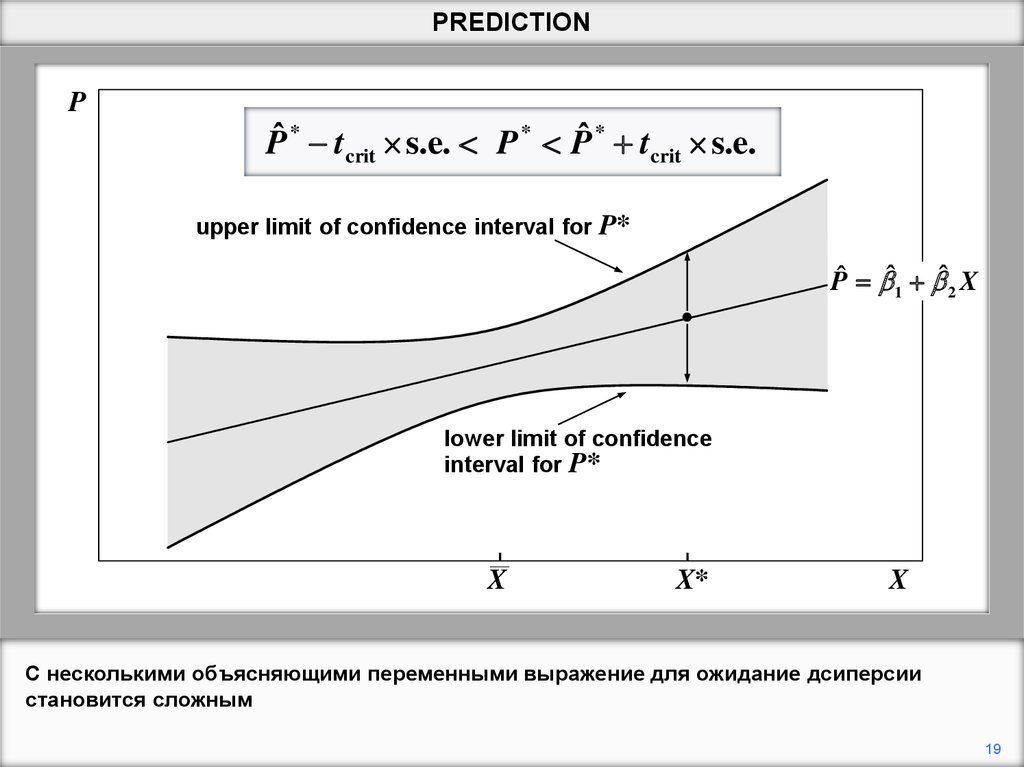
С несколькими объясняющими переменными выражение для ожидание дсиперсии
становится сложным
19

20.

PREDICTION
P
Pˆ * t crit s.e. P * Pˆ * t crit s.e.
upper limit of confidence interval for P*
Pˆ ˆ1 ˆ2 X
lower limit of confidence
interval for P*
0
50
100
X
150
X*
200
X250
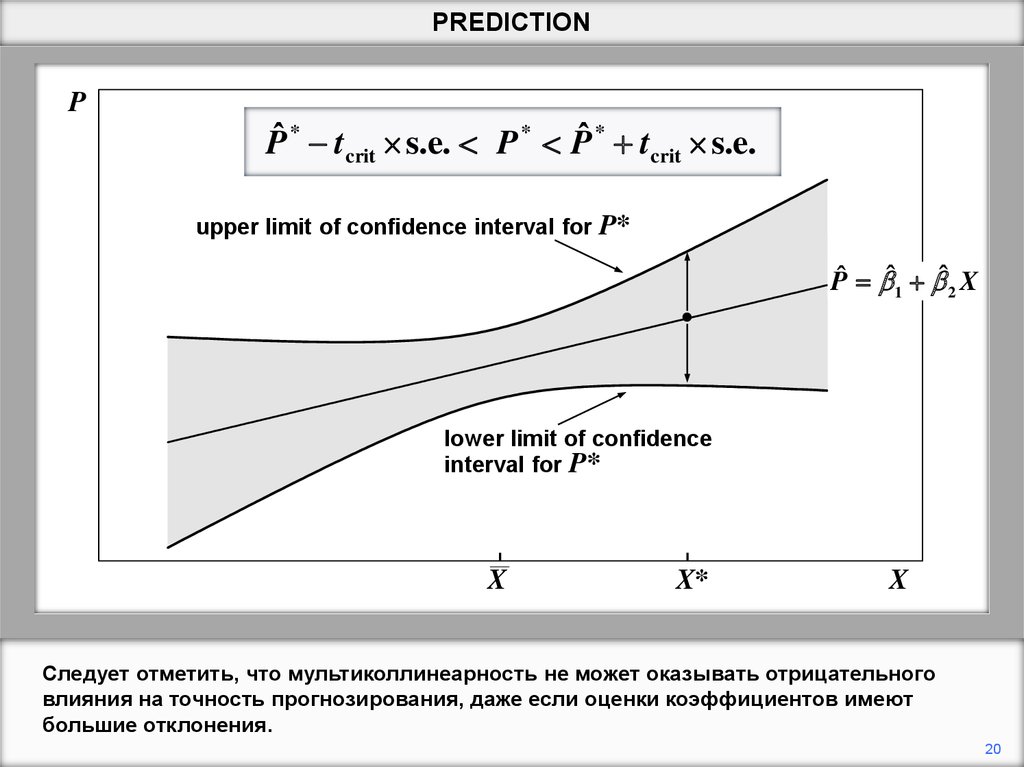
Следует отметить, что мультиколлинеарность не может оказывать отрицательного
влияния на точность прогнозирования, даже если оценки коэффициентов имеют
большие отклонения.
20

21.

PREDICTION
Y 1 2 X 2 3 X 3 u
Suppose X2 and X3 are positively correlated, 2 > 0, 3 > 0.
Then cov ˆ2 , ˆ3 0 .
If ˆ 2 is overestimated, ˆ 3 is likely to be underestimated.
So
ˆ X
2
*
2
ˆ3 X 3* may be a good estimator of 2 X 2* 3 X 3* .
Similarly, for other combinations.
Для простоты предположим, что есть две объясняющие переменные, что оба имеют
положительные истинные коэффициенты и как показано, они положительно
коррелированы; мы прогнозируем значение Y *, учитывая значения X2 * и X3 *.
21

22.

PREDICTION
Y 1 2 X 2 3 X 3 u
Suppose X2 and X3 are positively correlated, 2 > 0, 3 > 0.
Then cov ˆ2 , ˆ3 0 .
If ˆ 2 is overestimated, ˆ 3 is likely to be underestimated.
So
ˆ X
2
*
2
ˆ3 X 3* may be a good estimator of 2 X 2* 3 X 3* .
Similarly, for other combinations.
Тогда, если эффект от X2 переоценен, поэтому ˆ2 > β2, эффект от X3 вероятно будет
недооценена с ˆ 3< β3. Как следствие, эффекты ошибки могут в какой-то мере отмениться,
в результате линейная комбинация может быть приближена к (β2X2* + β3X3*)
22

23.

PREDICTION
Simulation
Y 10 2 X 2 3 X 3 u
X 2 {1, 2, 3, 4, ..., 17, 18, 19, 20}
X 3 {2, 2, 4, 4, ..., 18, 18, 20, 20}
rX 2 , X 3 0.9962
u ~ N 0,1
Y * ˆ1 ˆ2 X 2* ˆ3 X 3*
ˆ1 ˆ2 ˆ3 X 2*
Это будет проиллюстрировано с моделированием, с моделью и показанными
данными. Мы устанавливаем модель и делаем прогноз Y * ˆ1 ˆ2 X 2* ˆ3 X 3*
23

24.

PREDICTION
Simulation
Y 10 2 X 2 3 X 3 u
X 2 {1, 2, 3, 4, ..., 17, 18, 19, 20}
X 3 {2, 2, 4, 4, ..., 18, 18, 20, 20}
rX 2 , X 3 0.9962
u ~ N 0,1
Y * ˆ1 ˆ2 X 2* ˆ3 X 3*
ˆ1 ˆ2 ˆ3 X 2*
*
*
Поскольку X2 и X3 практически идентичны, они могут приблизиться к Y ˆ1 ˆ2 ˆ3 X 2
Таким образом, точность прогноза зависит как близко ˆ2 ˆ3 к (β2 + β3), то есть 5
24

25.

PREDICTION
10
ˆ2 ˆ3
5
standard deviation 0.04
ˆ 2
standard deviations 0.45
ˆ3
0
0
1
2
3
4
5
6
7
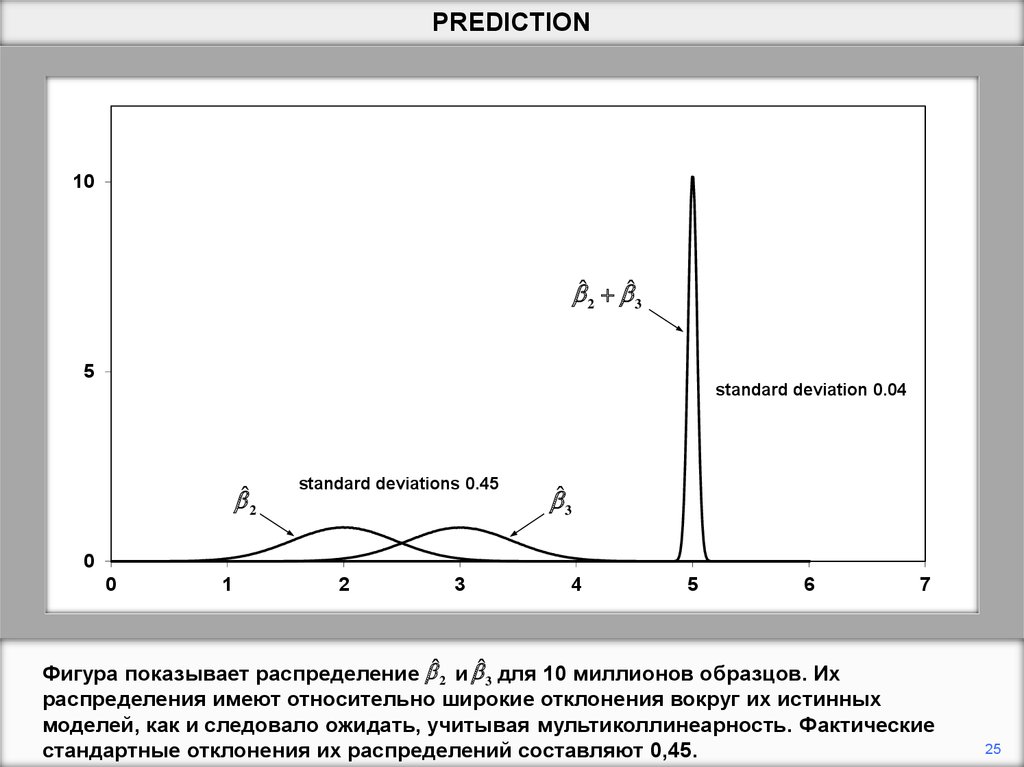
Фигура показывает распределение ˆ 2 и ˆ3 для 10 миллионов образцов. Их
раcпределения имеют относительно широкие отклонения вокруг их истинных
моделей, как и следовало ожидать, учитывая мультиколлинеарность. Фактические
стандартные отклонения их распределений составляют 0,45.
25

26.

PREDICTION
10
ˆ2 ˆ3
5
standard deviation 0.04
ˆ 2
standard deviations 0.45
ˆ3
0
0
1
2
3
4
5
6
7
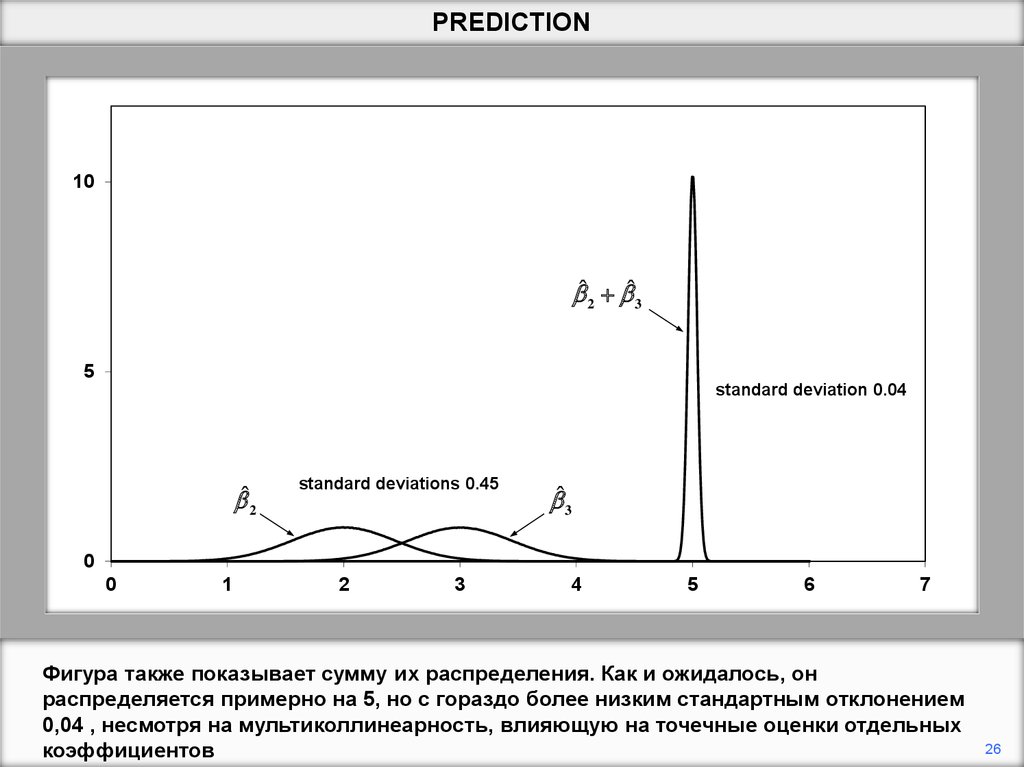
Фигура также показывает сумму их распределения. Как и ожидалось, он
распределяется примерно на 5, но с гораздо более низким стандартным отклонением
0,04 , несмотря на мультиколлинеарность, влияющую на точечные оценки отдельных
коэффициентов
26