Похожие презентации:
Анализ алгоритмов решения математических задач (Работа с числами разных форматов)
1. Анализ алгоритмов решения математических задач (Работа с числами разных форматов)
Лекция № 3Анализ алгоритмов
решения математических
задач
(Работа с числами разных
форматов)
Автор: Бабалова И.Ф.
Доцент, каф.12
2018 г.
1
2.
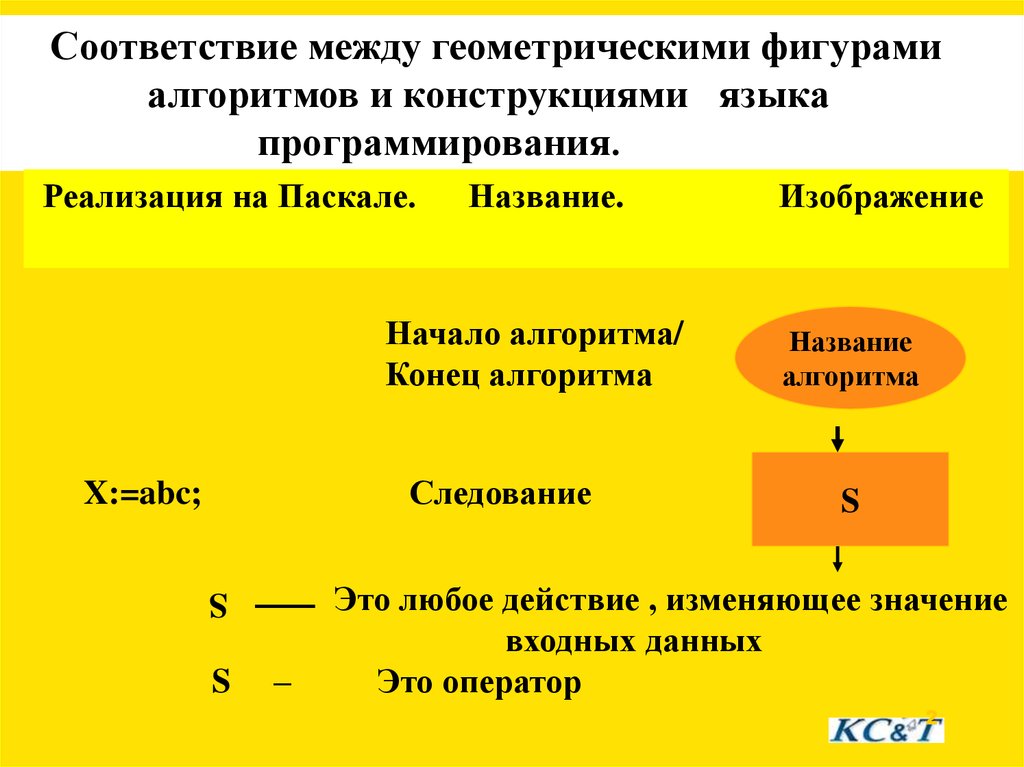
Соответствие между геометрическими фигурамиалгоритмов и конструкциями языка
программирования.
Реализация на Паскале.
Название.
Начало алгоритма/
Конец алгоритма
Следование
X:=abc;
S
S
–
Изображение
Название
алгоритма
S
Это любое действие , изменяющее значение
входных данных
Это оператор
2
3.
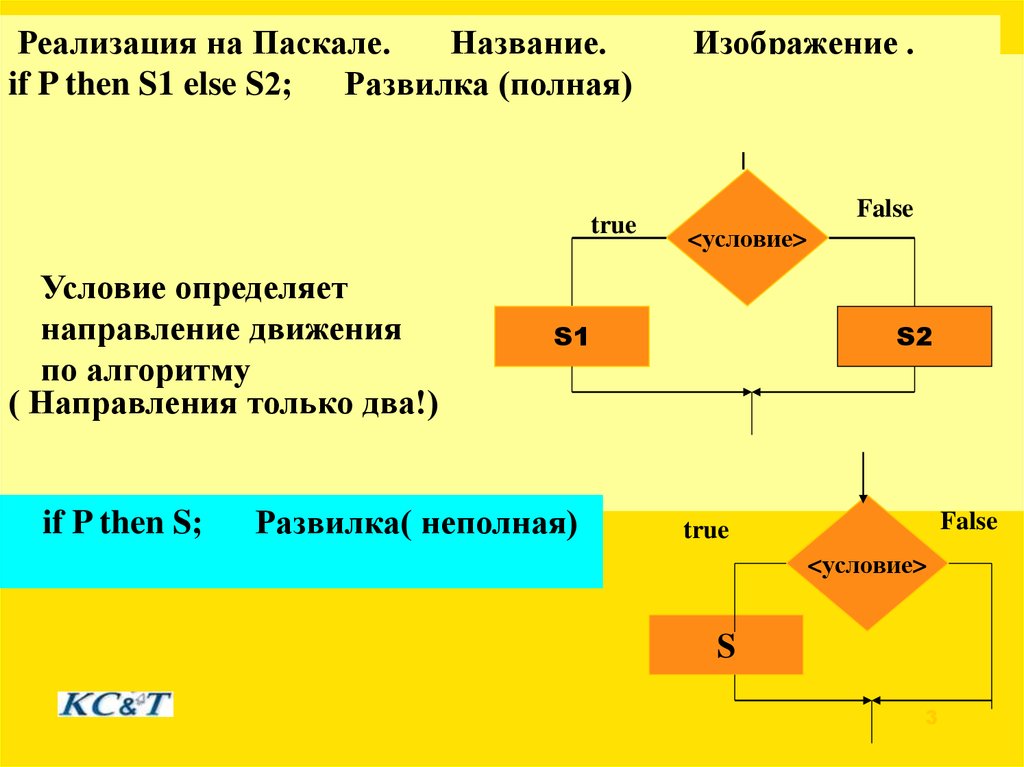
Реализация на Паскале.Название.
if P then S1 else S2;
Развилка (полная)
true
Условие определяет
направление движения
по алгоритму
( Направления только два!)
if P then S;
Изображение .
False
<условие>
S1
Развилка( неполная)
S2
False
true
<условие>
S
3
4.
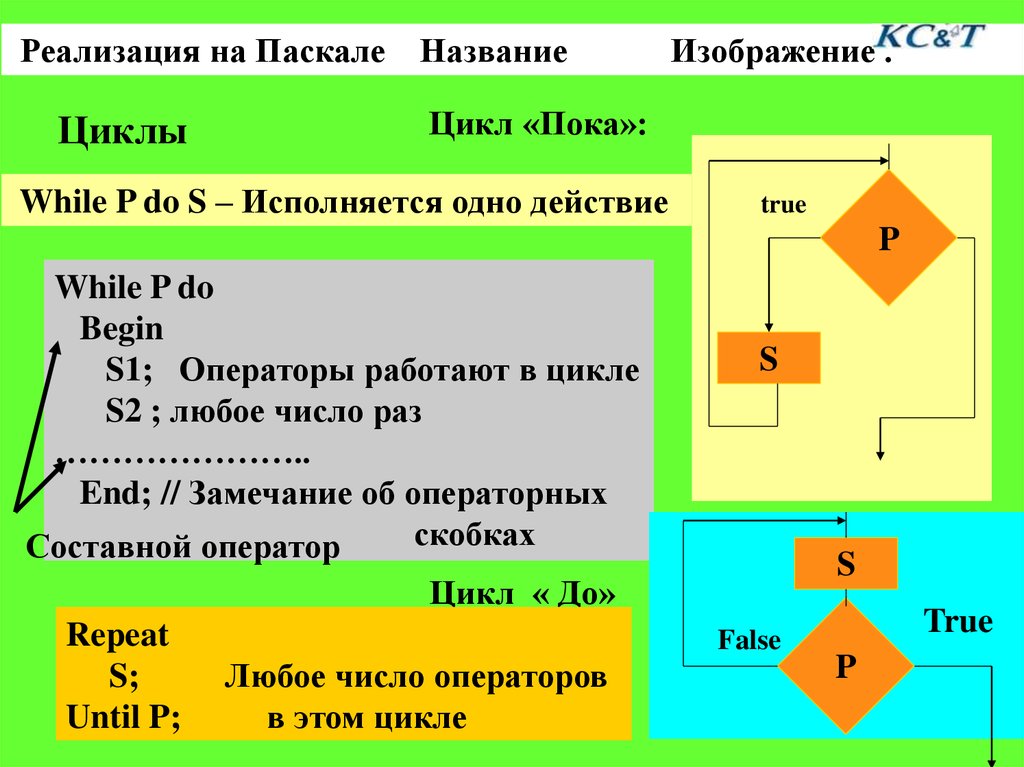
Реализация на Паскале НазваниеЦиклы
Изображение .
Цикл «Пока»:
While P do S – Исполняется одно действие
true
P
While P do
Begin
S1; Операторы работают в цикле
S2 ; любое число раз
…………………..
End; // Замечание об операторных
скобках
Составной оператор
S
S
Цикл « До»
Repeat
S;
Until P;
False
Любое число операторов
в этом цикле
True
P
4
5.
Реализация на Паскале.Название.
Изображение
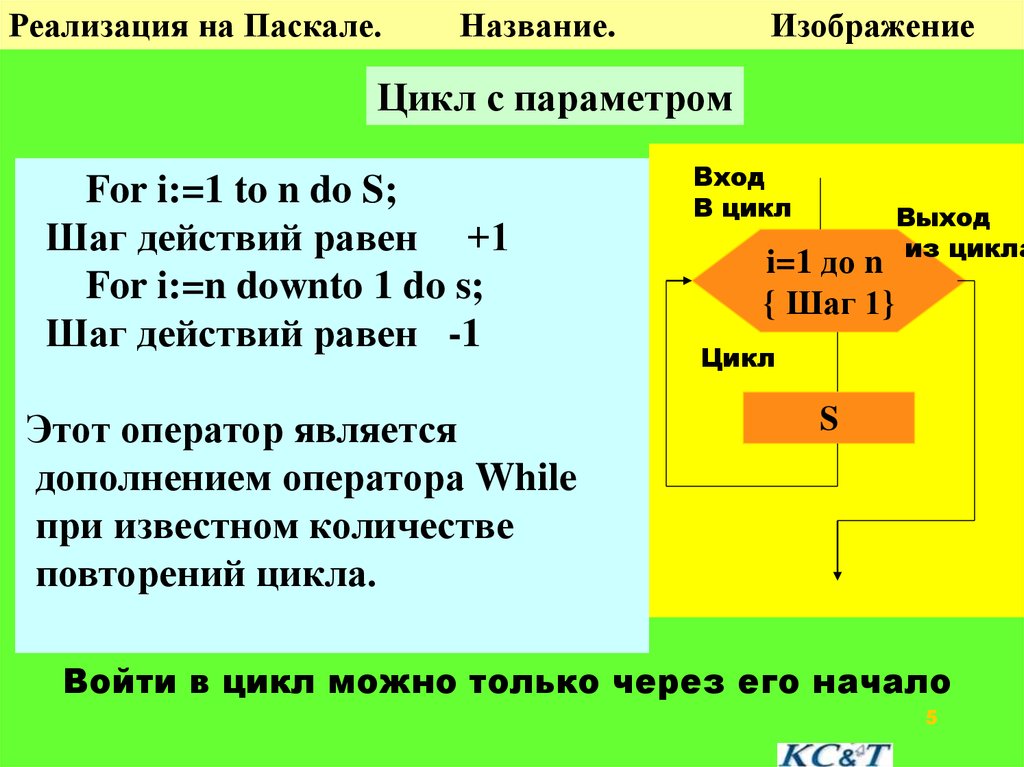
Цикл с параметром
For i:=1 to n do S;
Шаг действий равен +1
For i:=n downto 1 do s;
Шаг действий равен -1
Этот оператор является
дополнением оператора While
при известном количестве
повторений цикла.
Вход
В цикл
i=1 до n
{ Шаг 1}
Выход
из цикла
Цикл
S
Войти в цикл можно только через его начало
5
6.
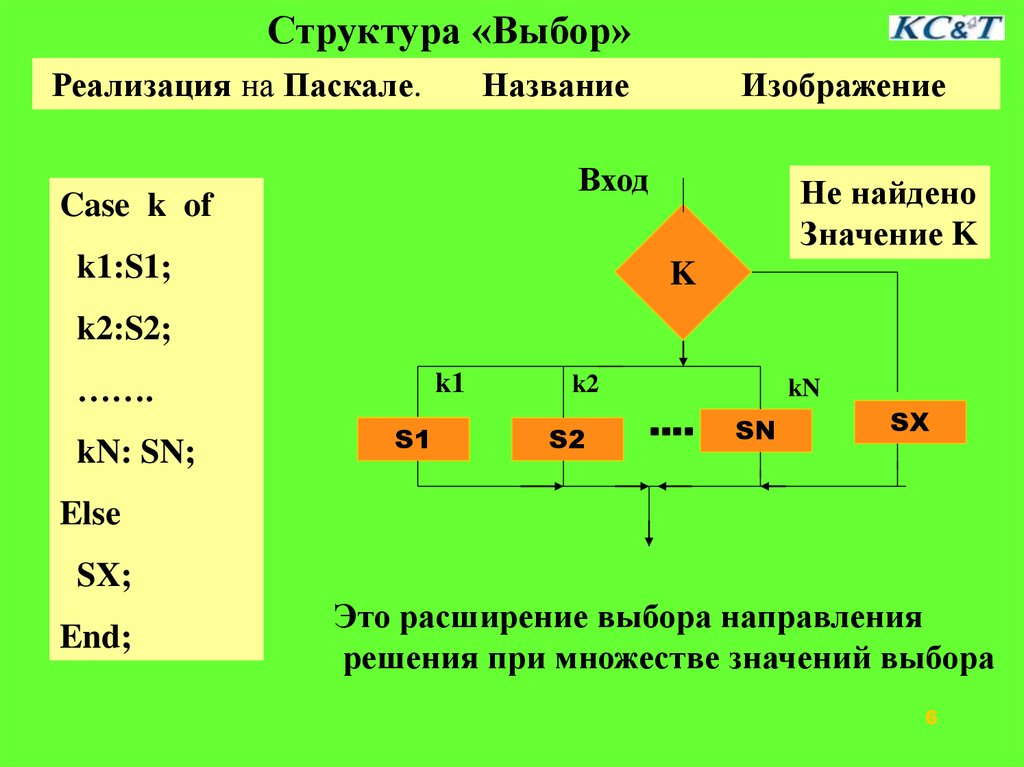
Структура «Выбор»Реализация на Паскале.
Название
Изображение
Вход
Case k of
k1:S1;
Не найдено
Значение K
K
k2:S2;
…….
kN: SN;
k1
S1
k2
S2
….
kN
SN
SX
Else
SX;
End;
Это расширение выбора направления
решения при множестве значений выбора
6
7.
Числовые алгоритмыВ числовых алгоритмах отражены основные концепции
теории чисел: делимость на заданное число,
разложение числа на множители, нахождение
наибольшего общего делителя двух чисел, деление по
модулю. Числовые алгоритмы необходимы для работы
со случайными числами.
Для генерации случайных чисел необходимо иметь
алгоритмы для выделения определенных разрядов
большого целого числа.
Числовые алгоритмы в настоящее время имеют большое
применение благодаря изобретению криптографических
схем, основанных на больших простых числах.
При разработке алгоритмов обработки чисел необходимо
уметь оценить время выполнения всех
арифметических операций.
7
8. Оценка времени работы алгоритмов
Размер входных данных определяется не количеством данных,а количеством битов для их записи.
Для перемножения двух β - битовых чисел обычным методом
потребуется количество битовых операций ~ θ (β2)
Задача разработчика
: создать такой
алгоритм,
x
x a 10
n
i 1
i
который бы выполнял арифметические операции за
наименьшее время.
Наиболее значимые алгоритмы: Поиск простых и
составных чисел, поиск общих делителей и наибольших
общих делителей, разложение числа на множители,
кодирование и декодирование чисел, генерация случайных
чисел. Для обработки целых чисел надо всегда помнить о
i 0
представлении целого числа в позиционной системе счисления:
n 1
x ai *10 i
i 0
где ai – цифры системы счисления
n –количество цифр в записи числа
8
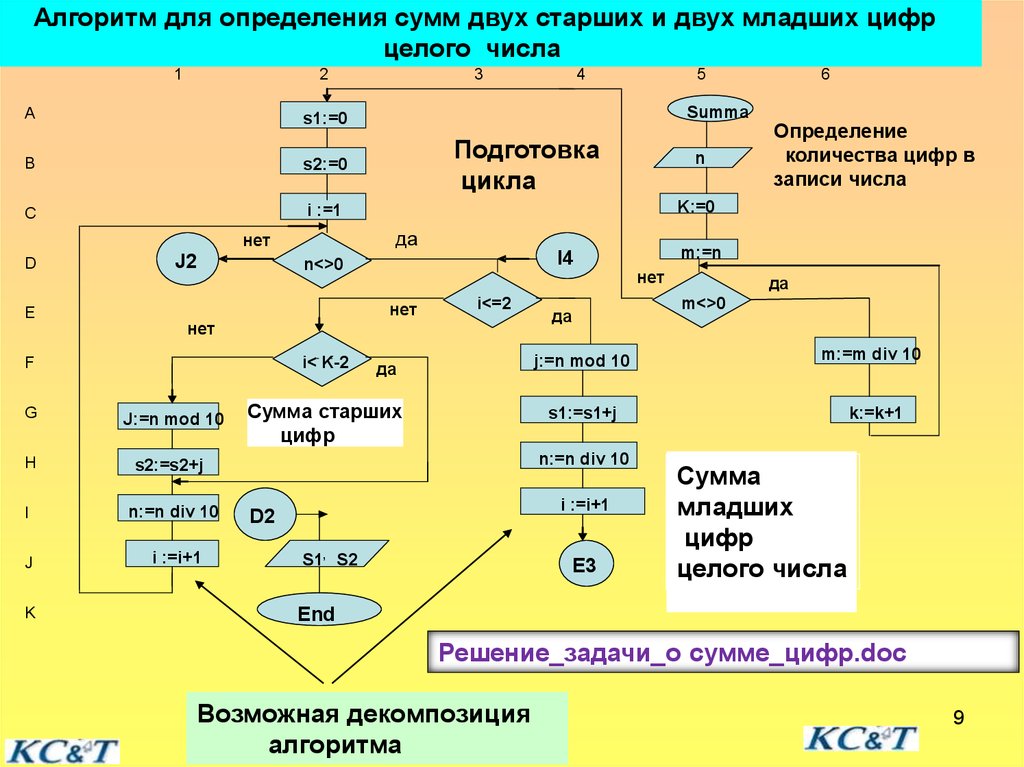
9.
Алгоритм для определения сумм двух старших и двух младших цифрцелого числа
1
2
A
s1:=0
B
s2:=0
C
i :=1
E
J2
G
i<- K-2
s2:=s2+j
I
n:=n div 10
J
i :=i+1
n
6
Определение
количества цифр в
записи числа
K:=0
I4
i<=2
нет
H
K
Подготовка
цикла
нет
J:=n mod 10
5
Summa
n<>0
F
4
да
нет
D
3
Сумма старших
цифр
?
нет
да
m<>0
да
j:=n mod 10
да
m:=n
m:=m div 10
s1:=s1+j
n:=n div 10
i :=i+1
D2
S1, S2
E3
k:=k+1
Сумма
младших
цифр
целого числа
End
Решение_задачи_о сумме_цифр.doc
Возможная декомпозиция
алгоритма
9
10. Вычисление рядов
Для вычисления рядов основным методом являетсяматематическая индукция:
n 1
n
1
1
S k k (n 1) n(n 1) (n 1) (n 1)(n 2)
2
2
k 1
k 1
1
Сумма всех к от 1 до n равна
S
n ( n 1)
2
S=1/2*n*(n+1)+(n+1)=(n*(n+1)+2*(n+1))/2=(n+1)*(n+2)/2
Мы показали, что формула оценки суммы верна как
для n слагаемых, так и для (n+1) слагаемого
Метод индукции справедлив не только для вычисления значений
сумм с заданной точностью, но и для оценки возможных границ
результатов вычислений рядов.
10
11. Вычисления с заданной точностью
Определение. В записи числа n цифр верные, еслиабсолютная погрешность записи числа не
превышает половины единицы разряда n –ой
значащей цифры:
234,563 число с верными цифрами
1
m n 1
*10
2
Погрешность его записи рана
=0.5*10-3
m=2, n=6 m-n+1=-3
В записи формулы m – это порядок числа, а n – количество
цифр в записи числа
Теорема.
Для сходящегося ряда к сумме S точность
вычислений не будет превышать ε при выполнении условия:
S S n
Sn S n 1
если
Имеем S1, S2, … , Sn-1, Sn - приближения к результату
11





 Информатика
Информатика








