Механіко-математична модель (теорія НДС) дорожнього одягу. Критерії граничного стану дорожнього одягу. Лекція № 3

1.

ЛЕКЦІЯ №3
з дисципліни ВС.3 “Механіка дорожніх одягів”
для спеціальності 192 «Будівництво та цивільна
інженерія»
за спеціалізаціями: “Технології будівельних
конструкцій, виробів і матеріалів”.
Лектор:
професор, доктор технічних наук
Мозговий Володимир Васильович
(завідувач кафедри дорожньо-будівельних
матеріалів і хімії, д.т.н., професор)

2. Вхідний контроль на лекції №3

1. З яких елементів складається дорожній одяг? Що таке покриття, які
функції воно виконує, які вимоги до матеріалів покриття?
2. Що таке основа, які функції воно виконує, які вимоги до матеріалів
основи? Що таке додаткова основа, які функції воно виконує, які вимоги до
матеріалів додаткової основи?
3. Які види дорожнього одягу за механічними властивостями та їх
особливості?
4. З яких етапів складається проектування дорожнього одягу? Мета збору
вихідних даних та які основні види інформації для цього використовуються?
Мета конструювання дорожнього одягу. Мета розрахунку дорожнього одягу.
Мета вибору раціонального варіанту.
5. На чому базуються сучасні емпіричні методи розрахунку? Мета
експерименту AASHO з випробувань дорожніх одягів? В чому полягала
методика експериментів AASHO з випробувань дорожніх одягів?
6. Як оцінювали стан кожної секції оцінювали в експериментах AASHO ?
Загальний вигляд моделі деградації конструкції дорожнього одягу.
Емпірична залежність показника PSI від показників характеристик стану
покриття.Емпірична залежність для приведеної товщини.
7. Номограми та методика розрахунку товщини дорожнього одягу за
результатами експериментів AASHO. Недоліки емпіричних методів. Які
задачі в сучасній практиці вирішуються на основі отриманих
загальнонаукових закономірностей в експериментах AASHO?
8. Що розуміють під розрахунковою схемою конструкції? Перша
розрахункова схема для розрахунку товщини дорожнього одягу. Які фактори
враховуються при удосконаленні розрахункової схеми? Дві головні складові
розрахункової схеми та їх суть.

3.

Тема лекції №3
Механіко-математична модель
(теорія НДС) дорожнього одягу.
Критерії граничного стану дорожнього
одягу

4. План лекції №3

1. Вимоги
до
механіко-математичних
моделей дорожнього одягу.
2. Механічна модель.
3. Основні
закономірності
напруженодеформованого стану.
4. Граничний стан будівельних об’єктів.
5. Розрахунок за несучою здатністю шарів
із зв’язних матеріалів.
6. Розрахунок за несучою здатністю шарів
із незв’язних матеріалів.

5. 1 Вимоги до механіко-математичних моделей дорожнього одягу

Визначення необхідної товщини дорожнього
одягу – складна задача, яка потребує відповідний
розрахунковий апарат. Розглянемо приклад, що
ілюструє ступінь складності цієї задачі.
Припустимо, що потрібно запроектувати
дорожній одяг із 4-х шарів: 2 шари –
асфальтобетон; щебеневий шар, піщаний шар.
Товщини а/б шарів і додаткової основи з піску
прийняті мінімально допустимими з умови
утворення стійкої структури. Зрозуміло, що
матеріал кожного шару і грунт характеризується
мінімум 1 – м показником експлуатаційних і 1 – м
показником міцнісних властивостей.

6.

Отже, відомо:
3 показника навантаження: тиск р, розмір
площі
контакту
D,
кількість
повторного
навантаження Np;
задані товщини 3 – х шарів: h1, h2, h3;
10 показників властивостей матеріалів: Еі, νі,
φі, Сі .
При цьому необхідно, щоб між шуканою
товщиною і кожним із показників був би
ідеальний логічний зв’язок. Порушення логічності
хоча б одного зв’язку сприймається інженером як
ознака
помилковості
методики
розрахунку
конструкції.

7.

Найбільш надійним способом визначення
товщини шарів дорожнього одягу і найбільш
вагомою основою для розуміння його поведінки
при зовнішній дії, є механіко-математична
модель,
що
базується
на
досягненнях
фундаментальних наук:
• механіка твердого деформованого тіла;
• теорія пружності;
• теорія в’язкопружності;
• теорія пластичності;
• опір матеріалів;
• механіка ґрунтів.

8. 2 Механічна модель

Механічну
модель
дорожнього
або
аеродромного одягу представляють як таку, що
складається із елементів 2-ох видів: шарів або
плит.
Модель плити (пластини) простіша, тому що
при її математичному викладі використовуються
спрощені гіпотези
Кирхгофа-Лява: гіпотеза
плоских нормалей, аналогічна гіпотезі плоских
перетинів при згині балки і гіпотеза про достатньо
(пренебрежимо) малі напруження по нормалях до
серединної площини плити, аналогічна гіпотеза
про відсутність взаємного контакту волокон
балки, що згинається, паралельних
до
нейтральної
осі.
Добре
підходить
для
цементобетону.

9.

Модель шару (прошарку) не містить цих
спрощень,
що
дозволяє
краще
описувати
деформації матеріалів дорожніх одягів.
Як, правило жорстке покриття моделюють
плитою, а нежорстке - шаром. У цьому полягає
перша відмінність механічних моделей жорстких і
нежорстких дорожніх одягів.

10.

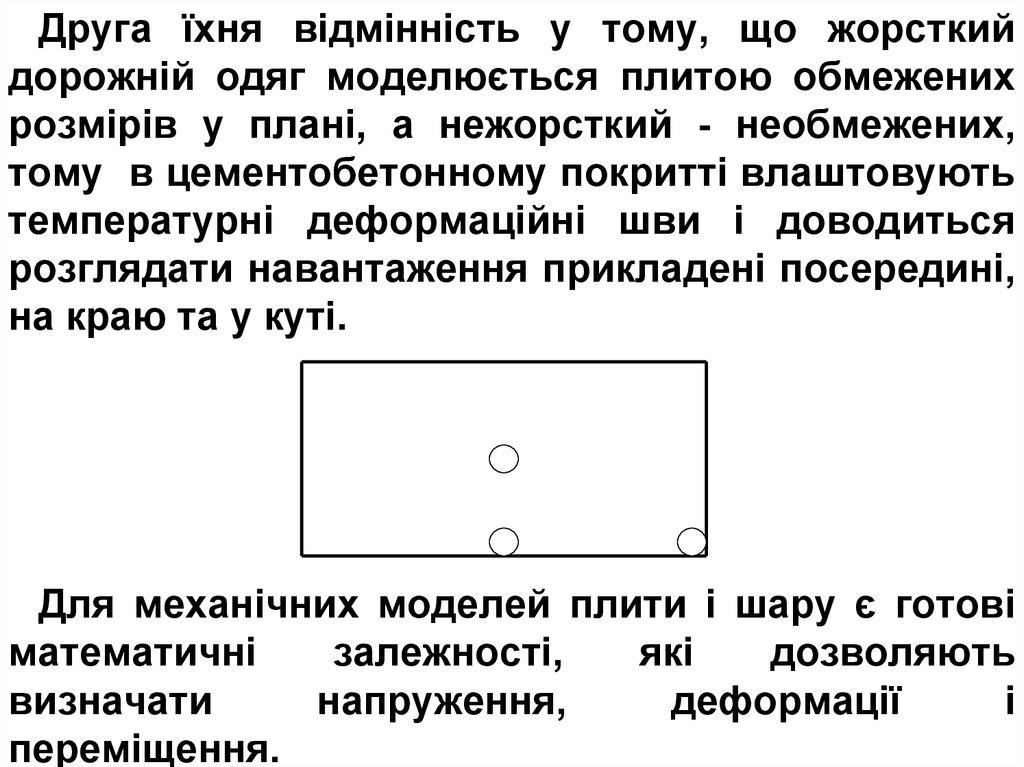
Друга їхня відмінність у тому, що жорсткий
дорожній одяг моделюється плитою обмежених
розмірів у плані, а нежорсткий - необмежених,
тому в цементобетонному покритті влаштовують
температурні деформаційні шви і доводиться
розглядати навантаження прикладені посередині,
на краю та у куті.
Для механічних моделей плити і шару є готові
математичні
залежності,
які
дозволяють
визначати
напруження,
деформації
і
переміщення.

11. 3 Основні закономірності напружено-деформованого стану

12. Однорідний пружній напівпростір

Дія навантаження, рівномірно розподіленого
по площі кола.
Вертикальні переміщення точок розміщених
під центром навантаження

13. Шаруватий пружний напівпростір

Його механічна модель являє собою пакет
пружних шарів, що мають необмежені розміри в
горизонтальному напрямку. Товщини шарів
можуть бути будь-які. Нижній шар має
необмежену товщину тобто є однорідним
напівпростором.
Прошарки зчеплені між собою на контактах,
тобто деформуються спільно, не відриваючись
один від одного і не просковзуючи один щодо
одного. Матеріал кожного шару характеризується
визначеним (відомою) значенням (величиною) Е
и ν. На зовнішній поверхні прикладене нормальне
навантаження.

14. Формула для загального модуля пружності двошарового напівпростору.

Загальним модулем пружності шаруватого
напівпростору називають таке значення модуля
пружності однорідного півпростору, при якому
прогини півпросторів рівні між собою.
Ця формула дає результат, близький до
номограми інструкції по розрахунку дорожнього
одягу.

15. Напруження в шаруватому напівпросторі

• напруження залежить не від модулів окремо, а
від їх співвідношення;
• щоб знизити σz у 4 рази, треба збільшити h1 у 2
рази або ж збільши Е1 у 8 раз (асфальтобетон
замість щебеню).

16. б) вид епюр:

від нормального
навантаження
від дотичного
навантаження

17. в) активна зона по згину верхнього шару

h1
h2
Е1
Е2
σ
(1)
r
hакт=h1(E1/E2)1/2
Якщо h2> hакт,
Е3
σ
(1)
r
не залежить від Е3
Практичні наслідки:
• достатньо призначити h2> hакт, щоб при
слабкому ґрунті σr(1) не залежало від Егр;
• прошарок
щебеню
між
старим
цементобетонним
покриттям
і
новим
асфальтобетонним не повинен бути більшим 1012 см.

18. г) Навантаження на краї або над тріщиною