Построение графиков, содержащих выражение под знаком модуля

1. Построение графиков, содержащих выражения под знаком модуля

2. Частный случай (под знаком модуля одно выражение и нет слагаемых без модуля)

1) построить график функции, опустив знак
модуля
2) отобразить симметрично оси Ох часть
графика, расположенного в области
отрицательных значений у.

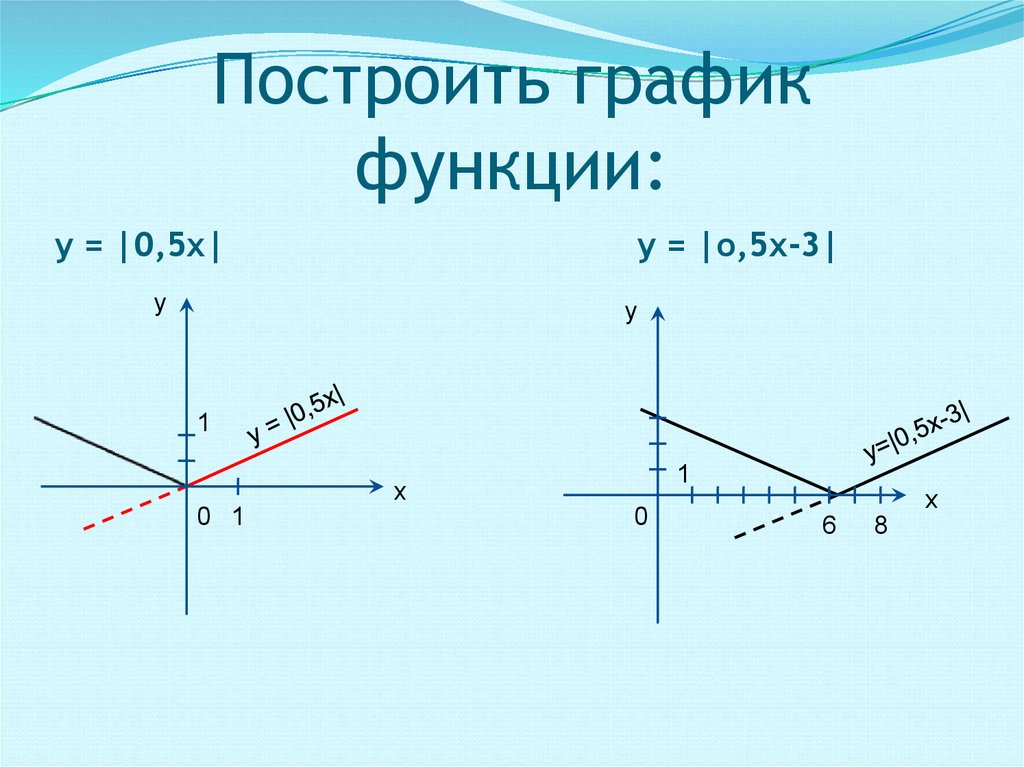
3. Построить график функции:

у = |0,5х|
у = |о,5х-3|
у
у
1
1
х
0 1
0
х
6
8

4. Построение графиков, содержащих выражения под знаком модуля

1) найти корни выражений, стоящих под знаком
модуля;
2) на числовой прямой проставить эти корни;
3) в каждом промежутке определить вид
функции;
4) построить график в каждом промежутке.

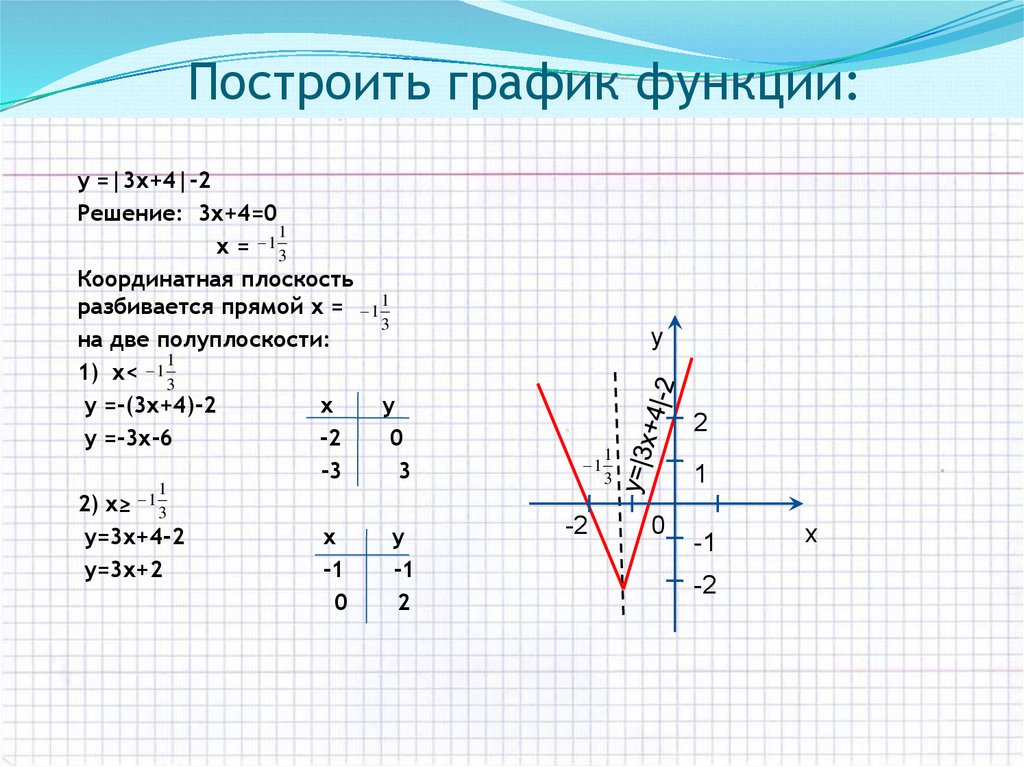
5. Построить график функции:

у =|3х+4|-2
Решение: 3х+4=0
1
х = 1 3
Координатная плоскость
разбивается прямой х = 1 1
3
на две полуплоскости:
1
1) х< 1 3
у =-(3х+4)-2
х
у
у =-3х-6
-2
0
-3
3
1
2) х≥ 1 3
у=3х+4-2
х
у
у=3х+2
-1
-1
0
2
у
2
1
-2
1
3
1
0
-1
-2
х

6. Построить график функции:

у=|х-1| -|2 - х| + 2
Решение: х=1
1) х<1
у=-х+1-2+х+2
у=1
2) -1 ≤ х≤ 2
у=х-1-2+х+2
у=2х-1
3) х>2
у =х-1+2-х+2
у=3
у
х=2
х
1
2
у
1
3
3
2
1
0
1 2
у=|х-1| - |2-х| +2
х

7. Практические упражнения

a) y=|х-1|+|х-2|+х слайд №9
b) y=|3х|-3х слайд №10
c) y=|х-3|+|1-х|+4 слайд №10
d) y=|5-х|-|2-х|-3 слайд №11
e) y=7 -|х-1|+|х+5| слайд №11
f) y=|х-5|+|5-х| слайд №12
k) y=-|3-х|+|2-х|-3 слайд №12
l) y=|13 х-2|+|3+ 23 х|-3 слайд №13

8. a) у=|х - 1|+|2 - х| +2

Решение:
у
у=|х-1|-|2-х|+2
3
2
1
0
1
2
х
х=1; х=2
1) х< 1
у=-х+1-2+х+2
у=1
2) 1≤х≤ 2
у=х-1-2+х+2
у=2х -1
3) х>2
у=х-1+2-х+2
у=3
х у
1 1
2 3

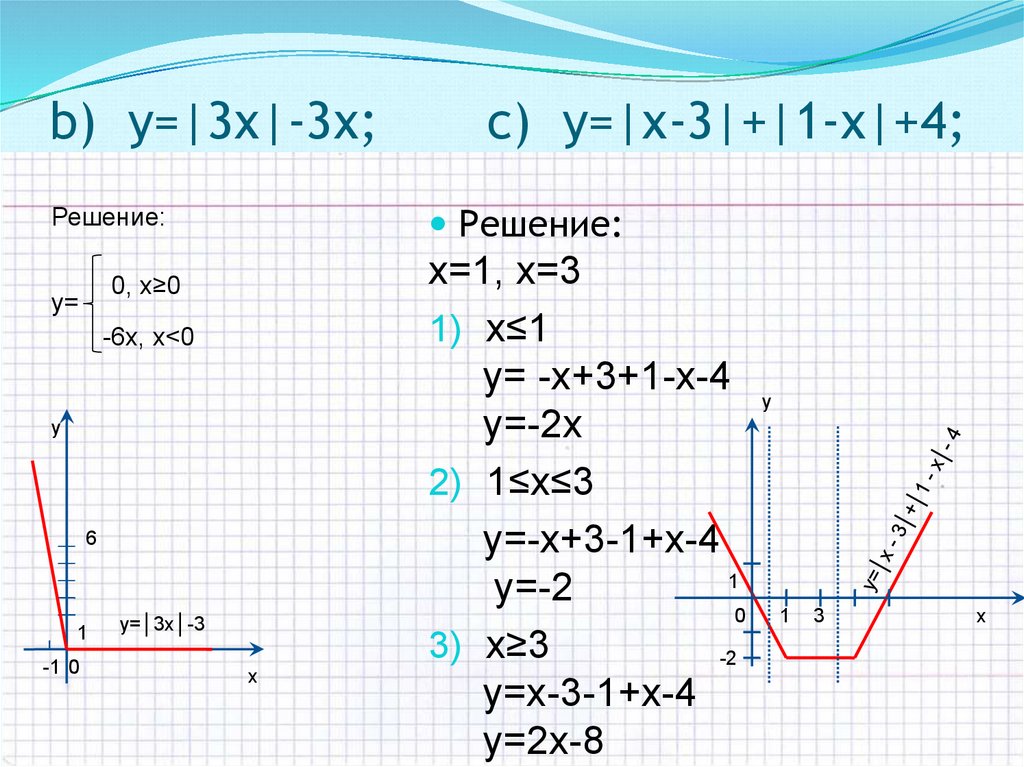
9. b) y=|3х|-3х; c) y=|х-3|+|1-х|+4;

b) y=|3х|-3х;
Решение:
Решение:
0, х≥0
y=
-6х, х<0
y
6
1
-1 0
c) y=|х-3|+|1-х|+4;
y=│3x│-3
x
х=1, х=3
1) x≤1
y= -x+3+1-x-4
y=-2x
2) 1≤x≤3
y=-x+3-1+x-4
1
y=-2
0
3) x≥3
-2
y=x-3-1+x-4
y=2x-8
y
1
3
x

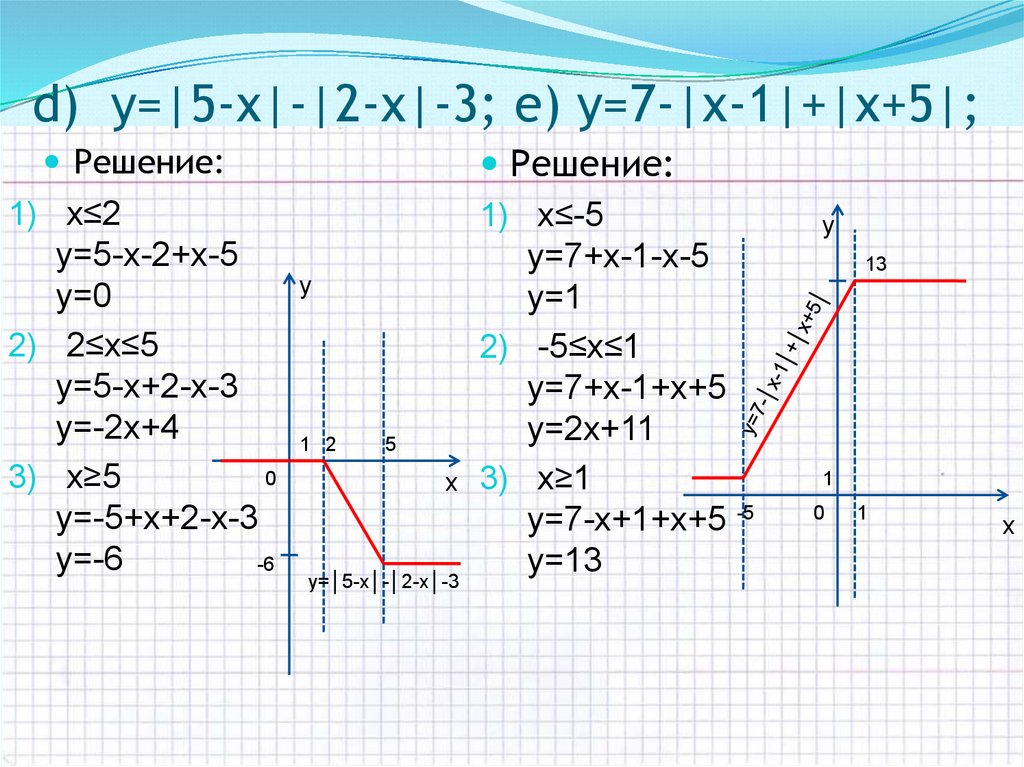
10. d) y=|5-х|-|2-х|-3; e) y=7-|х-1|+|х+5|;

Решение:
1) х≤2
y=5-х-2+х-5
y=0
2) 2≤х≤5
y=5-х+2-х-3
y=-2х+4
0
3) x≥5
y=-5+х+2-х-3
y=-6
-6
y
1 2
5
x
y=│5-x│-│2-x│-3
Решение:
1) х≤-5
y=7+х-1-х-5
y=1
2) -5≤х≤1
y=7+х-1+х+5
y=2х+11
3) x≥1
y=7-х+1+х+5 -5
y=13
y
13
1
0
1
x

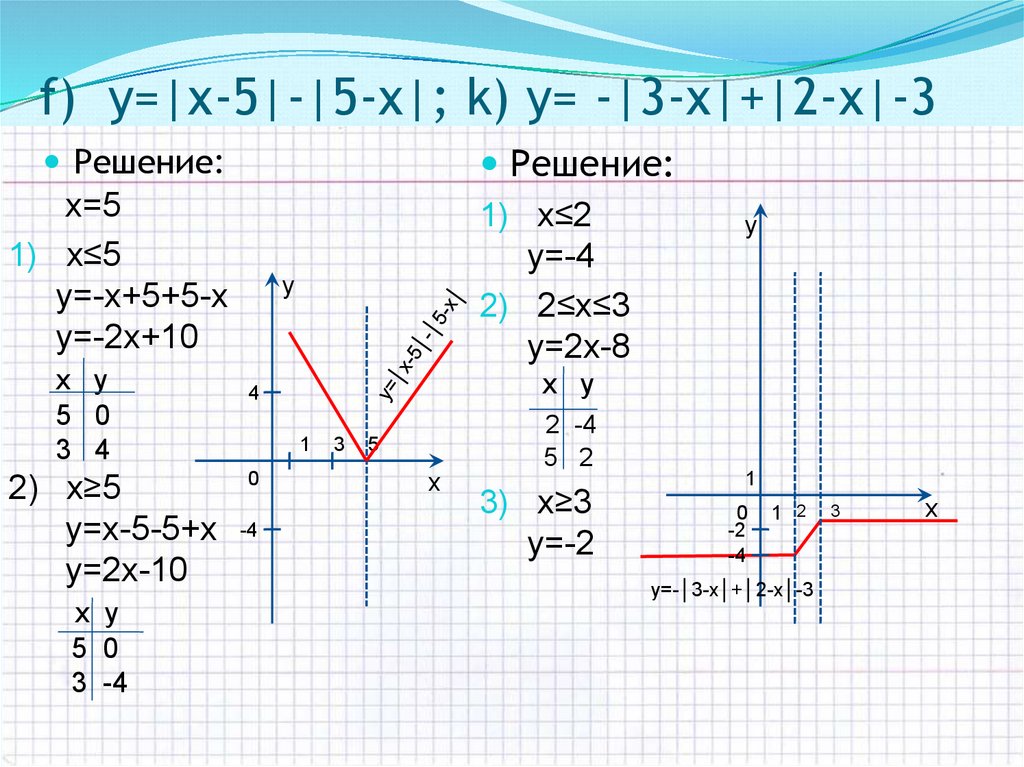
11. f) y=|х-5|-|5-х|; k) y= -|3-х|+|2-х|-3

Решение:
x=5
1) х≤5
y=-х+5+5-х
y=-2х+10
x y
5 0
3 4
2) x≥5
y=x-5-5+x
y=2x-10
x y
5 0
3 -4
Решение:
1) х≤2
y=-4
2) 2≤х≤3
y=2х-8
y
x y
4
1
0
-4
y
3
2 -4
5 2
5
x
3) x≥3
y=-2
1
0
-2
-4
1 2
y=-│3-x│+│2-x│-3
3
x

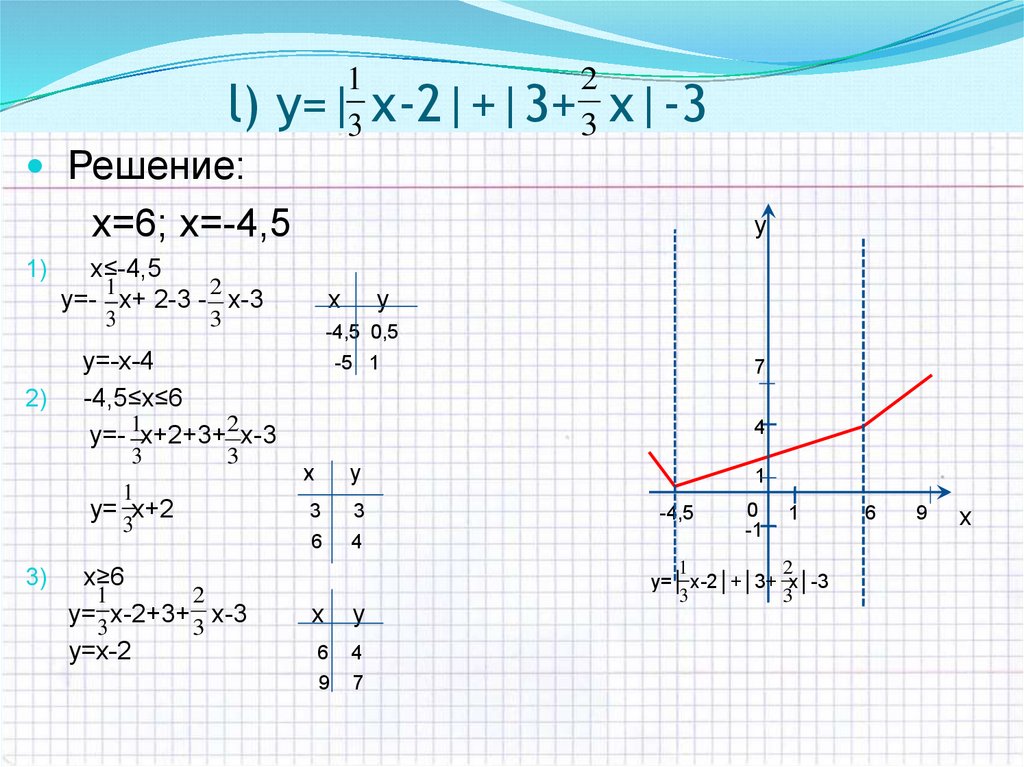
12. l) y=| х-2|+|3+ х|-3

l)
2
1
y=|3 х-2|+|3+ 3
х|-3
Решение:
x=6; х=-4,5
1)
х≤-4,5
1
2
y=- х+ 2-3 - х-3
3
2)
х
3
у
-4,5 0,5
y=-х-4
-4,5≤х≤6
y=- 1x+2+3+2 x-3
3
3
1
y= x+2
3
3)
y
x≥6
1
2
y= 3 x-2+3+ 3 x-3
y=x-2
-5 1
7
4
х
у
3
3
6
4
х
у
6
9
4
7
1
-4,5
0
-1
1
1
2
y=│ x-2│+│3+ x│-3
3
3
6
9
x

13. Вывод:

Решите уравнение: │х-3│+│1-х│=4
(х=3; х=1)
Постройте график функции: y= │х-3│+│1-х│- 4
Имея корни решенного уравнения и
рассматривая график построенной функции,
делаем вывод: корни данного уравнения – это
координаты точки пересечения графика с осями
координат.
Таким образом строим графики функций,
содержащие выражения под знаком модуля
опираясь на решение уравнения, содержащего
выражения под знаком модуля.

14. Занимательная графика

y
Построив графики нескольких
функций в одной прямоугольной
системе координат, получим
некое «произведение искусств».
6
. .
2
-1 0
1
3
4
6
7
х