Похожие презентации:
Медианы, биссектрисы и высоты треугольника
1.
2.
№ 93Отрезки AE и DC пересекаются в точке B, являющейся
серединой каждого из них. а) Докажите, что
треугольники ABC и EBD равны; б) наудите углы A и C
треугольника ABC, если в треугольнике BDE D = 47о,
E = 42о.
C Дано: AB = BE, BD = BC,
D = 47о, E = 42о
A
1
47о
Док-ть:
Найти:
B
2
42о
D
E
AB = BE (по усл.)
1=
ΔABС
= ΔEBD
Aи
C
Решение:
СУС
ΔABС
= ΔEBD
2 (верт.)
ВС = ВD (по усл.)
Ответ: 42о и 47о
A=
E = 42o
C=
D = 47o
3.
№ 96Дано: OA = OD, OB = OC,
1 = 74о,
3
4
Док-ть:
ΔAОB
Найти:
ACD
2 = 36о
= ΔDOC
Решение:
OA = OD (по усл.)
3=
СУС
ΔAOB
= ΔDOC
4 (верт.)
OB = OC (по усл.)
ACD =
2+
Ответ: 110о
DCO =
DCO =
2+
1
1 = 74o + 36o = 110o
4.
№ 99На сторонах угла CAD отмечены точки B и E так, что
точка B лежит на отрезке AC, а точка E – на отрезке
AD, причем AC = AD и AB = AE. Докажите, что CBD =
= DEC.
A
Дано: AC = AD, AB = AE
Док-ть:
B 2
1
?
?
DEC
E
D
C
AC = AD (по усл.)
A=
CBD =
Решение:
СУС
ΔACE
= ΔADB
A
AЕ = AВ (по усл.)
CBD = 180o –
2
DEC = 180o –
1
1=
CBD =
2
DEC
чтд
5.
25.10.2018К л а с с н а я р а б о т а.
Медианы, биссектрисы и
высоты треугольника.
6.
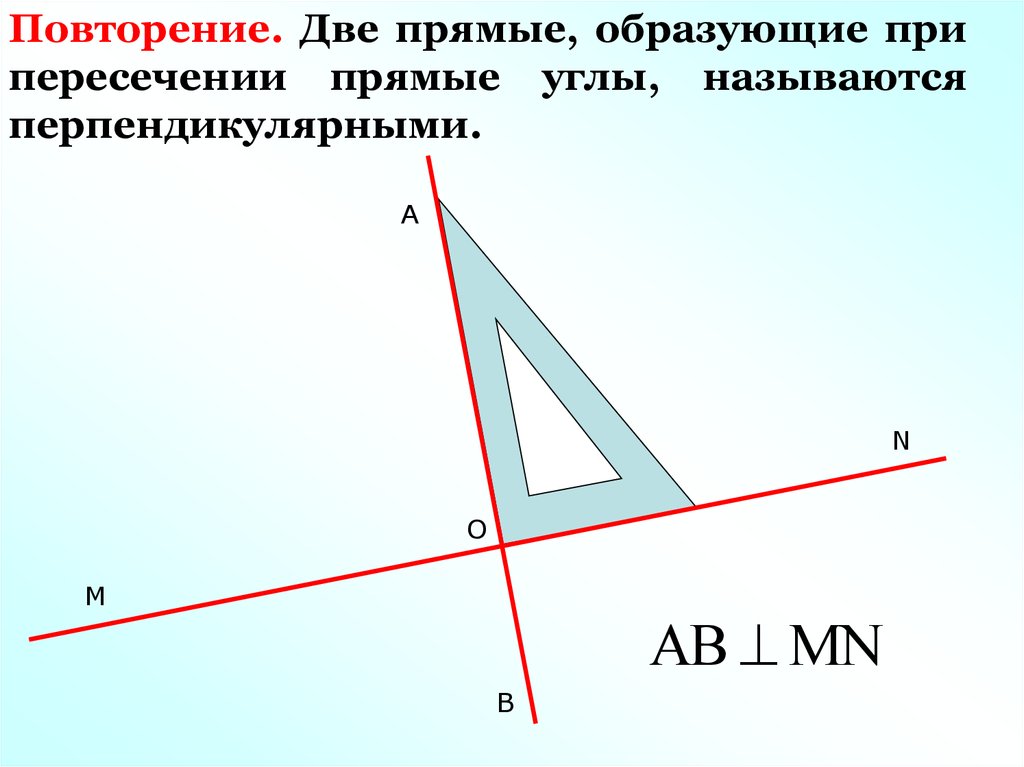
Повторение. Две прямые, образующие припересечении прямые углы, называются
перпендикулярными.
A
N
O
M
АВ MN
B
7.
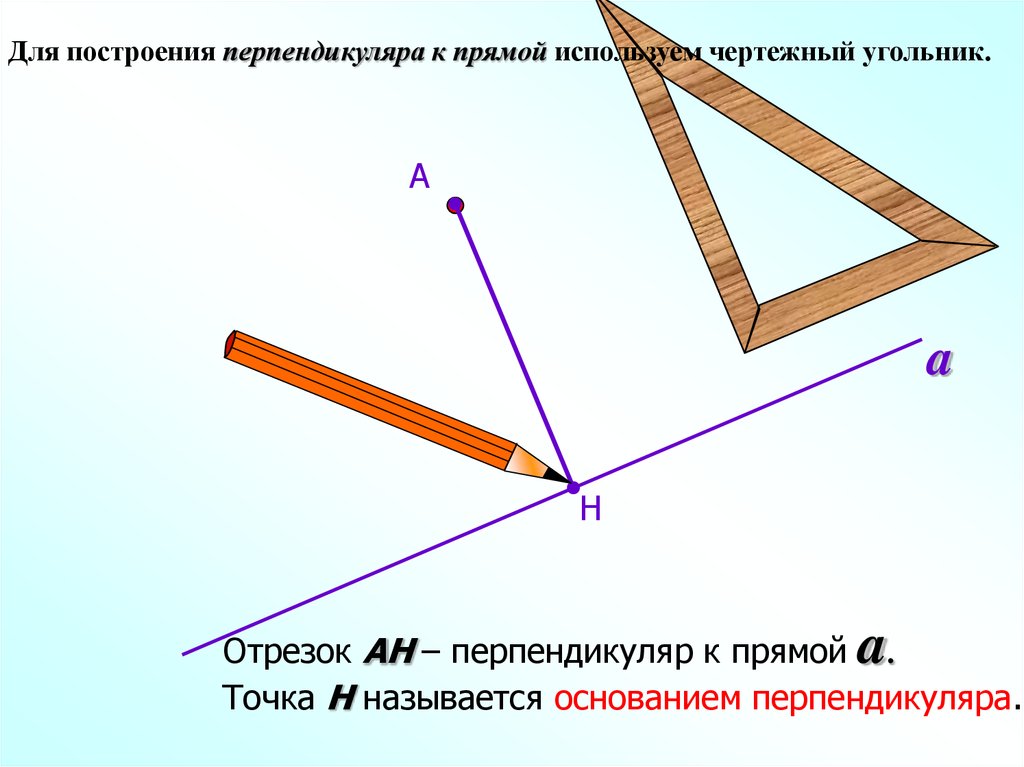
Для построения перпендикуляра к прямой используем чертежный угольник.А
a
Н
a
Отрезок АН – перпендикуляр к прямой .
Точка Н называется основанием перпендикуляра.
8.
Отрезок, соединяющий вершину треугольника с серединойпротивоположной стороны, называется медианой треугольника.
Перпендикуляр, проведенный из вершины треугольника к прямой,
содержащей противоположную сторону, называется высотой
треугольника.
медиана
высота
биссектриса
В
Ы
С
О
Т
А
Отрезок биссектрисы угла треугольника, соединяющий вершину
треугольника с точкой противоположной стороны, называется
1
биссектрисой треугольника.
9.
Медиана треугольника.Постройте медиану АК данного треугольника.
Постройте,
самостоятельно,
остальные медианы
этого
треугольника.
10.
ВQ
С
М
O
N
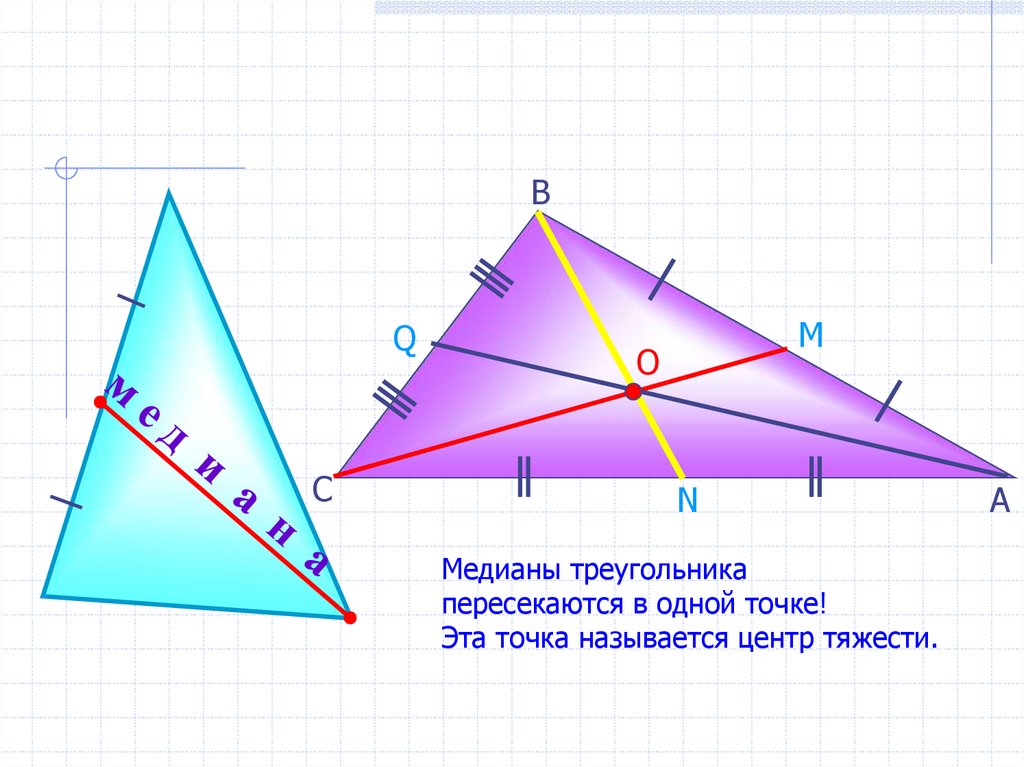
Медианы треугольника
пересекаются в одной точке!
Эта точка называется центр тяжести.
А
11.
Треугольник, который опирается на острие иглы в точке пересечениямедиан, находится в равновесии! Точка, обладающая таким
свойством, называется центром тяжести треугольника.
Треугольник, который опирается на опору по линии медианы,
находится в равновесии.
12. Постройте все биссектрисы данного треугольника.
Постройтевсе биссектрисы
данного
Биссектриса
треугольника
треугольника.
А
В
С
13.
OЭта точка тоже замечательная – точка пересечения биссектрис
является центром вписанной окружности.
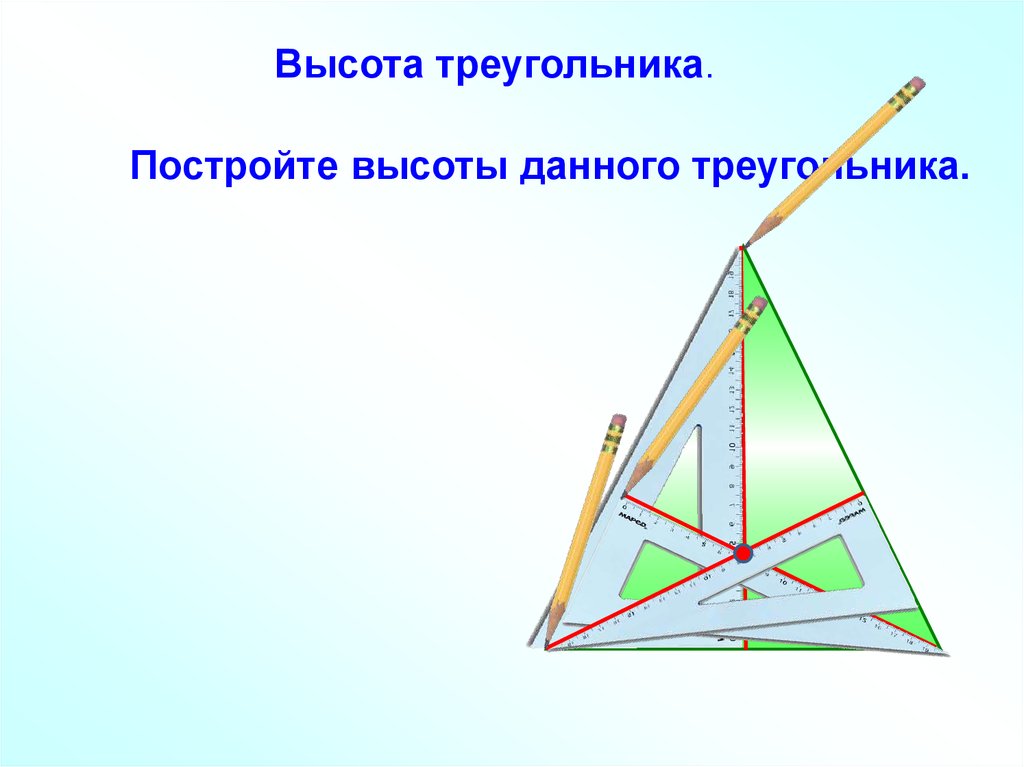
14. Высота треугольника.
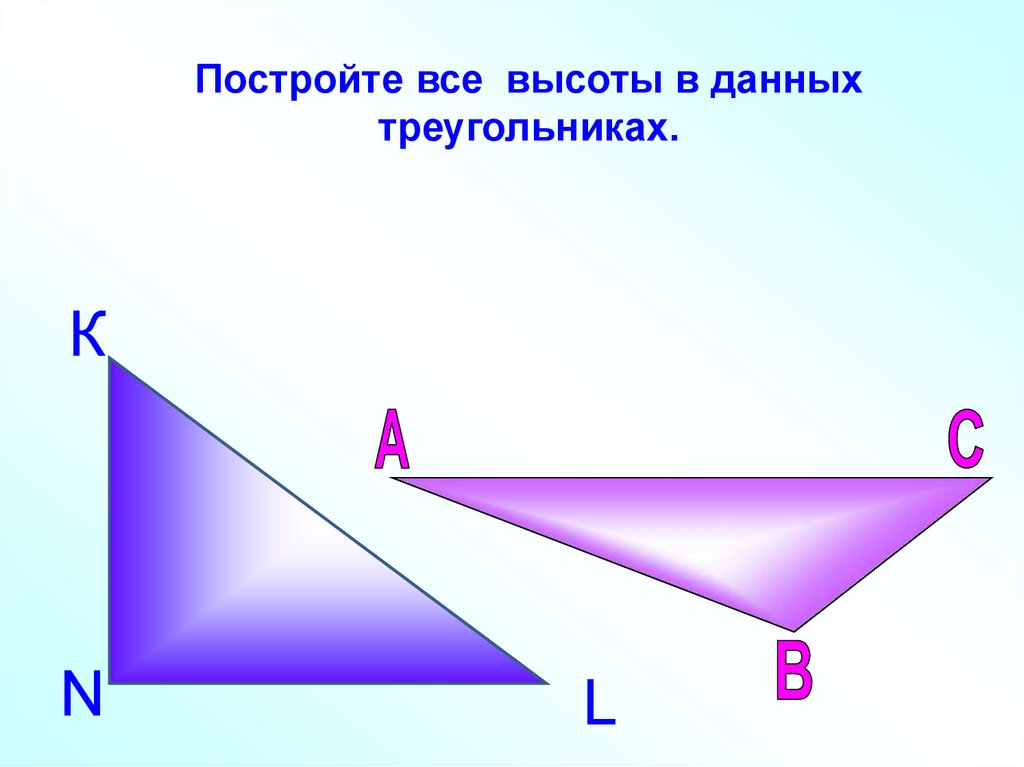
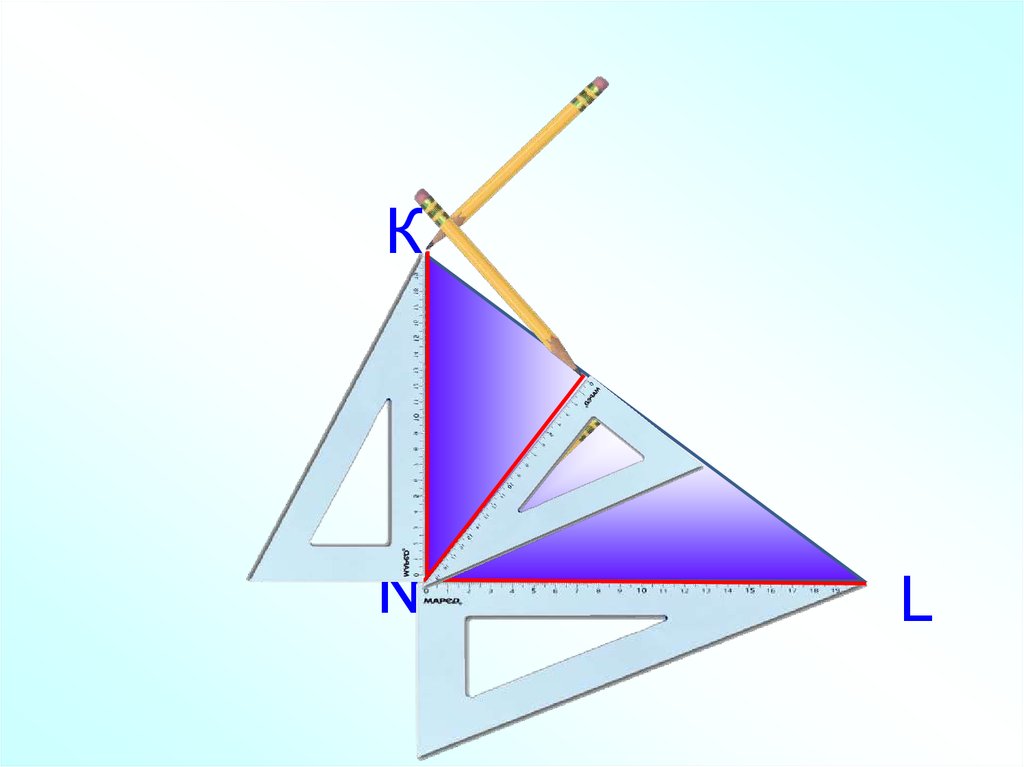
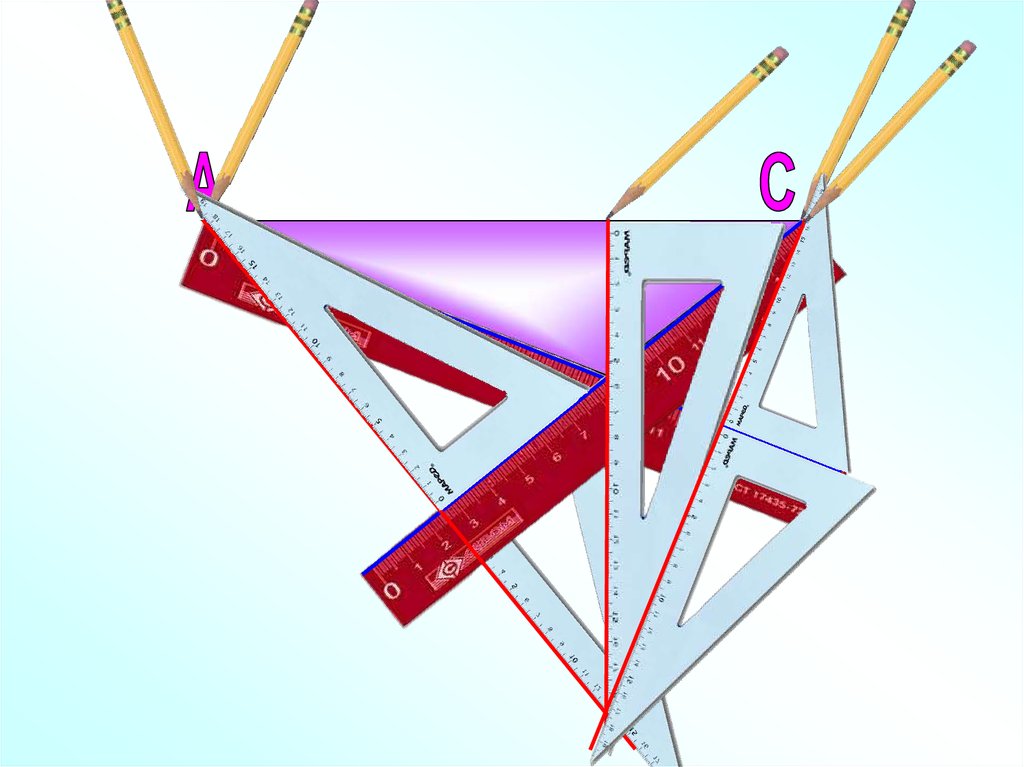
Постройте высоты данного треугольника.15. Постройте все высоты в данных треугольниках.
КN
L
16.
КN
L
17.
18.
Высоты прямоугольного треугольника пересекаются в вершине С.Высоты остроугольного треугольника пересекаются в точке О,
которая лежит во внутренней области треугольника.
В
Точка пересечения
O
высот называется –
ортоцентр.
М
Т
В
А
С
O
С
К
А
Высоты тупоугольного треугольника пересекаются в точке О,
которая лежит во внешней области треугольника.
19.
Перпендикуляр, проведенный из вершины треугольника к прямой,содержащей противоположную сторону, называется высотой
треугольника.
В
Ы
С
О
Т
А
1
В
Ы
С
О
Т
А
1
В
Ы
С
О
Т
А
Высота в прямоугольном
треугольнике, проведенная из
вершины острого угла,
совпадает с катетом.
1
Высота в тупоугольном
треугольнике, проведенная из
вершины острого угла,
проходит во внешней области
треугольника.
20.
п. 16,17, вопросы 5-9 (стр.50).Решить задачи № 103(на
отдельном листе), 105.
21.
Как называется отрезок АО?О
Медиана
биссектриса
А
высота
О
Медиана
биссектриса
высота
А
А
В
Ы
С
О
Т
А
О
Медиана
биссектриса
высота
22.
На рисунке построены высота, биссектриса, медиана.Щелкни мышкой на ответ, который ты считаешь верным.
Биссектриса
Медиана
СО ВК СМ
О
СО
В
ВК
Высота
СО
СМ ВК
М
С
СМ
К
А
23.
О каком отрезке это определение. а) Щёлкни мышкой по названию.б) Щёлкни мышкой по чертежу, где ты нашел этот отрезок.
Перпендикуляр, проведенный из вершины треугольника
к прямой, содержащей противоположную сторону…
биссектриса
молодец!
медиана
высота
В
Ы
С
О
Т
А
Щелкни мышкой по другим картинкам.
24.
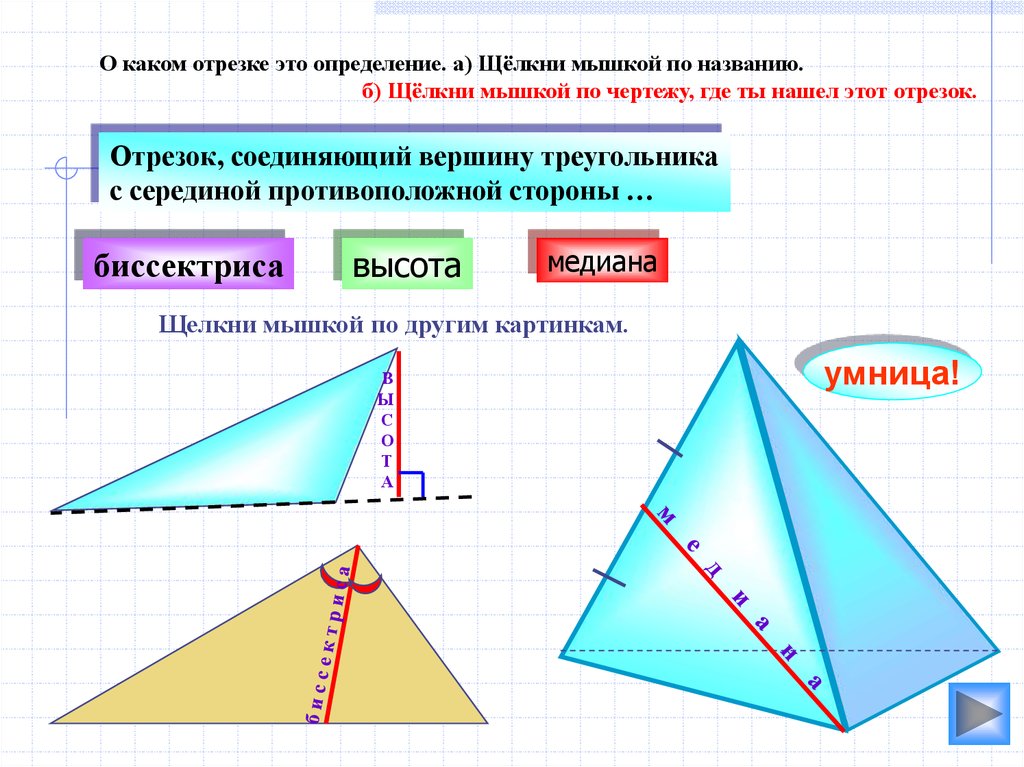
О каком отрезке это определение. а) Щёлкни мышкой по названию.б) Щёлкни мышкой по чертежу, где ты нашел этот отрезок.
Отрезок, соединяющий вершину треугольника
с серединой противоположной стороны …
биссектриса
высота
медиана
Щелкни мышкой по другим картинкам.
В
Ы
С
О
Т
А
умница!
















 Математика
Математика








