Похожие презентации:
Структурные превращения в деформированных кристаллах. Движущие силы рекристаллизации
1.
Тема 5Процессы, ответственные за формирование структуры
и текстуры в электротехнических сталях. Структурные
превращения в сталях. Движущие силы
рекристаллизации
Подготовил,
к.т.н.
А.А. Редикульцев
Екатеринбург
2018
2. ПРОЦЕССЫ, ПРОТЕКАЮЩИЕ ПРИ НАГРЕВЕ ДЕФОРМИРОВАННОГО МЕТАЛЛА
1. Возврат1.1 Отдых
1.2 Полигонизация
2. Рекристаллизация
2.1 Первичная рекристаллизация (ПР)
2.2 Собирательной рекристаллизации или нормальный рост зерен (НР).
2.3 Вторичная рекристаллизация (ВР) или аномальный рост зерен.
3. РЕКРИСТАЛЛИЗАЦИЯ
Монография Humphreys F.J., Hatherly M. Recrystallization and related Annealing Phenomen.ELSEVIER Ltd, Oxford, 2004. 574 p.
«Не просто написать книгу о рекристаллизации, потому что, хотя это четко определенная
тема, многие аспекты не очень хорошо поняты, а экспериментальные данные часто
являются недостаточными и противоречивыми. Всегда желательно, чтобы все
количественные аспекты явления выводились теоретически из первых принципов.
Однако в настоящее время это не представляется возможным, и читатель найдет в книге
смесь относительно надежных теорий с разумными предположениями и откровенными
догадками. Существуют две основные причины отсутствия прогресса в понимании данной
проблемы. Во-первых, мы не можем глубоко понимать процессы возврата и
рекристаллизации до тех пор, пока мы не поймем природу предшествующего им
деформированного состояния, а это в настоящее время является задачей далекого
будущего. Во-вторых, хотя некоторые процессы отжига, такие как возврат и рост зерен
являются относительно однородными, другие, такие как первичная рекристаллизация и
аномальный рост являются гетерогенными, и опираются на локальную нестабильность
материала, вызывая у исследователя параллели с явно случайными событиями,
например погодой»
4.
Пластическая деформация кристалловДля монокристаллов деформация осуществляется:
- скольжением дислокаций;
- двойникованием.
Для поликристаллов,
проскальзывание.
кроме
того,
возможно
зернограничное
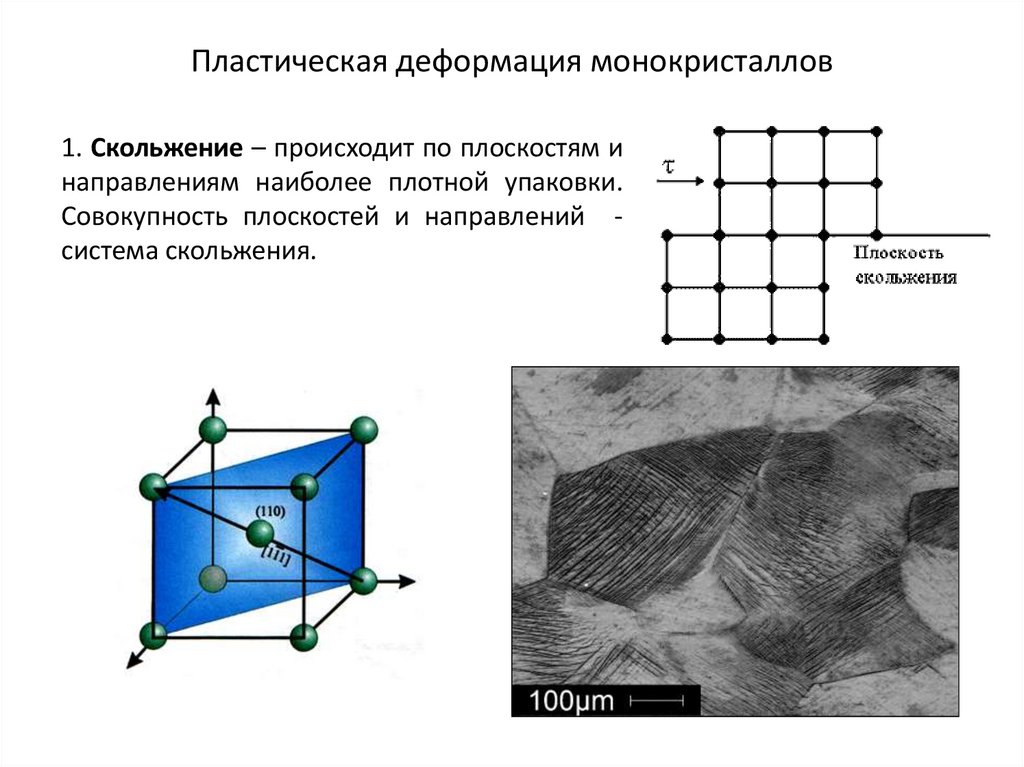
5. Пластическая деформация монокристаллов
1. Скольжение – происходит по плоскостям инаправлениям наиболее плотной упаковки.
Совокупность плоскостей и направлений система скольжения.
6.
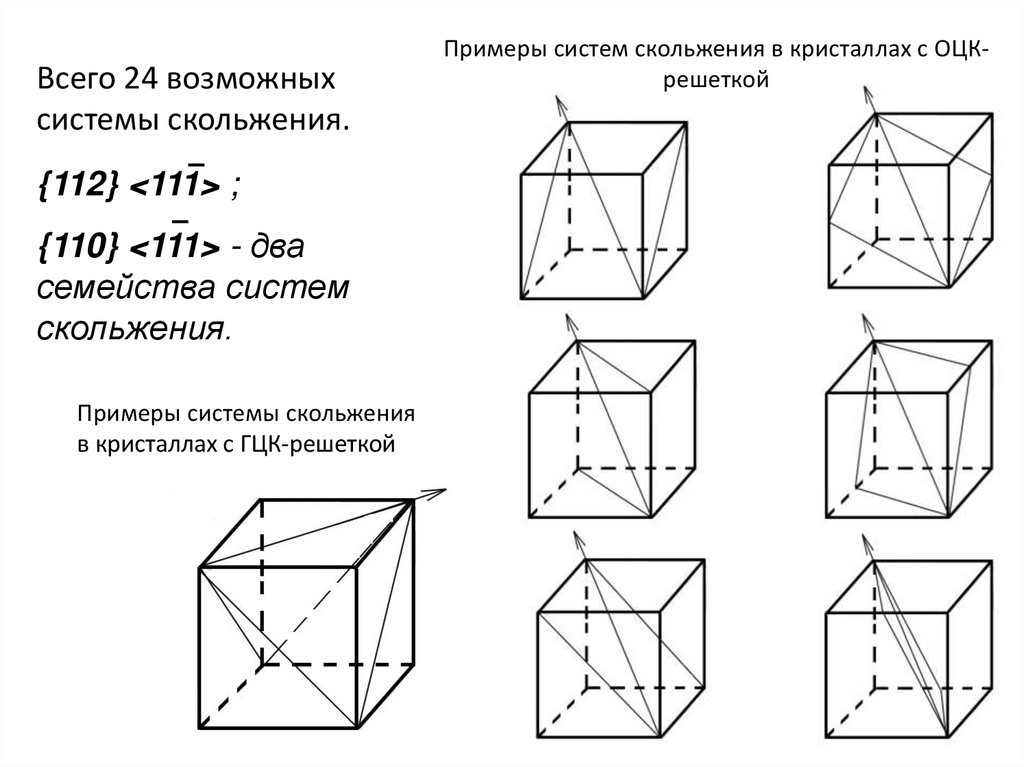
Всего 24 возможныхсистемы скольжения.
{112} <111> ;
{110} <111> - два
семейства систем
скольжения.
Примеры системы скольжения
в кристаллах с ГЦК-решеткой
Примеры систем скольжения в кристаллах с ОЦКрешеткой
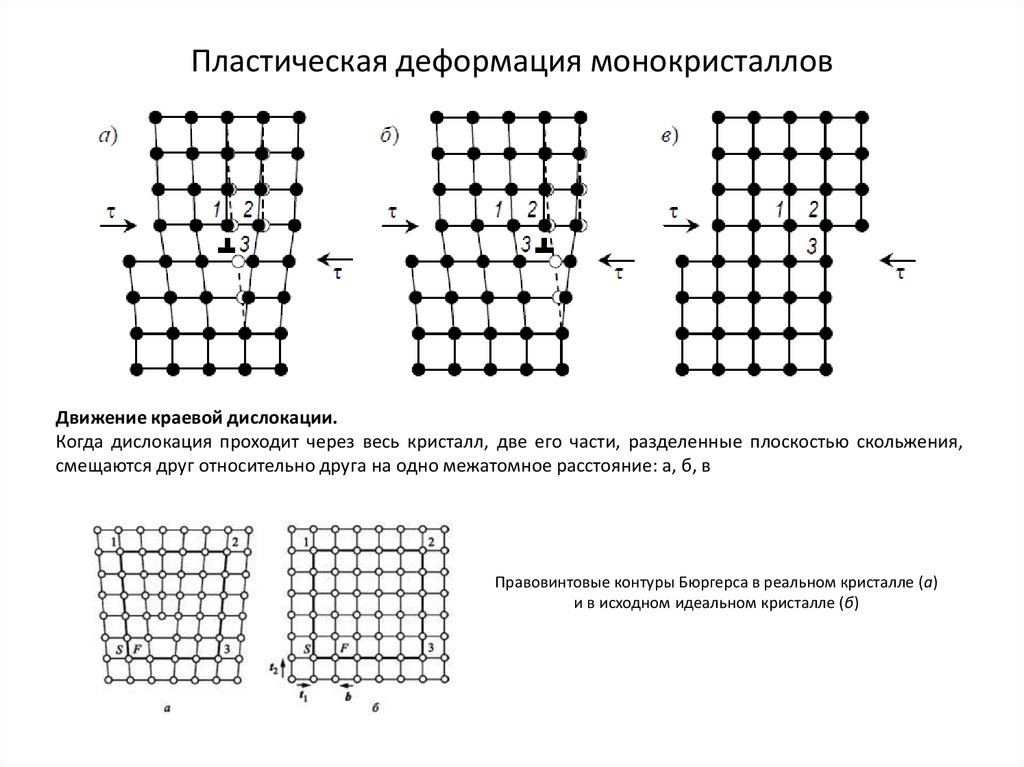
7. Пластическая деформация монокристаллов
Движение краевой дислокации.Когда дислокация проходит через весь кристалл, две его части, разделенные плоскостью скольжения,
смещаются друг относительно друга на одно межатомное расстояние: а, б, в
Правовинтовые контуры Бюргерса в реальном кристалле (а)
и в исходном идеальном кристалле (б)
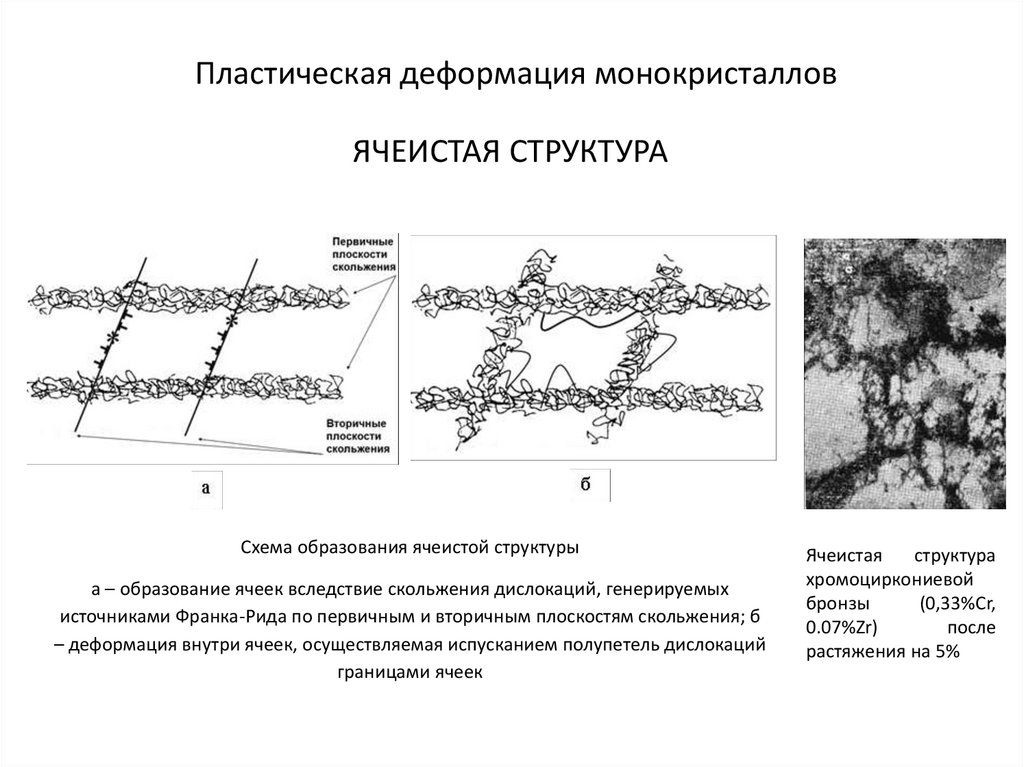
8. Пластическая деформация монокристаллов
ЯЧЕИСТАЯ СТРУКТУРАСхема образования ячеистой структуры
а – образование ячеек вследствие скольжения дислокаций, генерируемых
источниками Франка-Рида по первичным и вторичным плоскостям скольжения; б
– деформация внутри ячеек, осуществляемая испусканием полупетель дислокаций
границами ячеек
Ячеистая
структура
хромоциркониевой
бронзы
(0,33%Cr,
0.07%Zr)
после
растяжения на 5%
9.
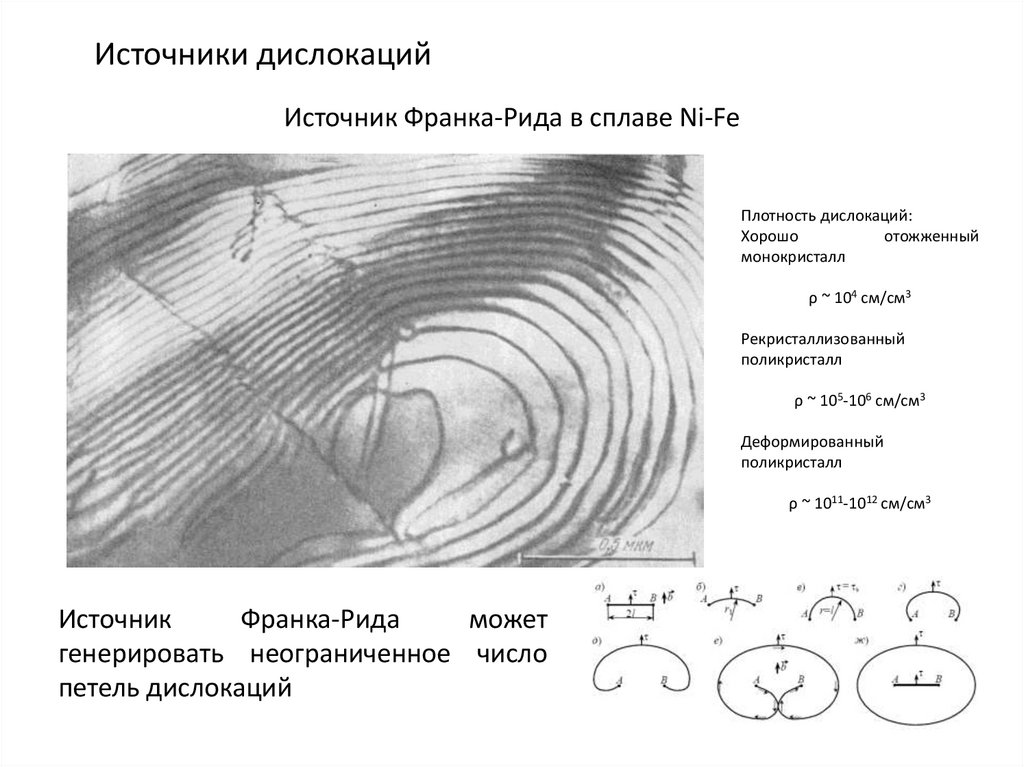
Источники дислокацийИсточник Франка-Рида в сплаве Ni-Fe
Плотность дислокаций:
Хорошо
отожженный
монокристалл
ρ ~ 104 см/см3
Рекристаллизованный
поликристалл
ρ ~ 105-106 см/см3
Деформированный
поликристалл
ρ ~ 1011-1012 см/см3
Источник
Франка-Рида
может
генерировать неограниченное число
петель дислокаций
10.
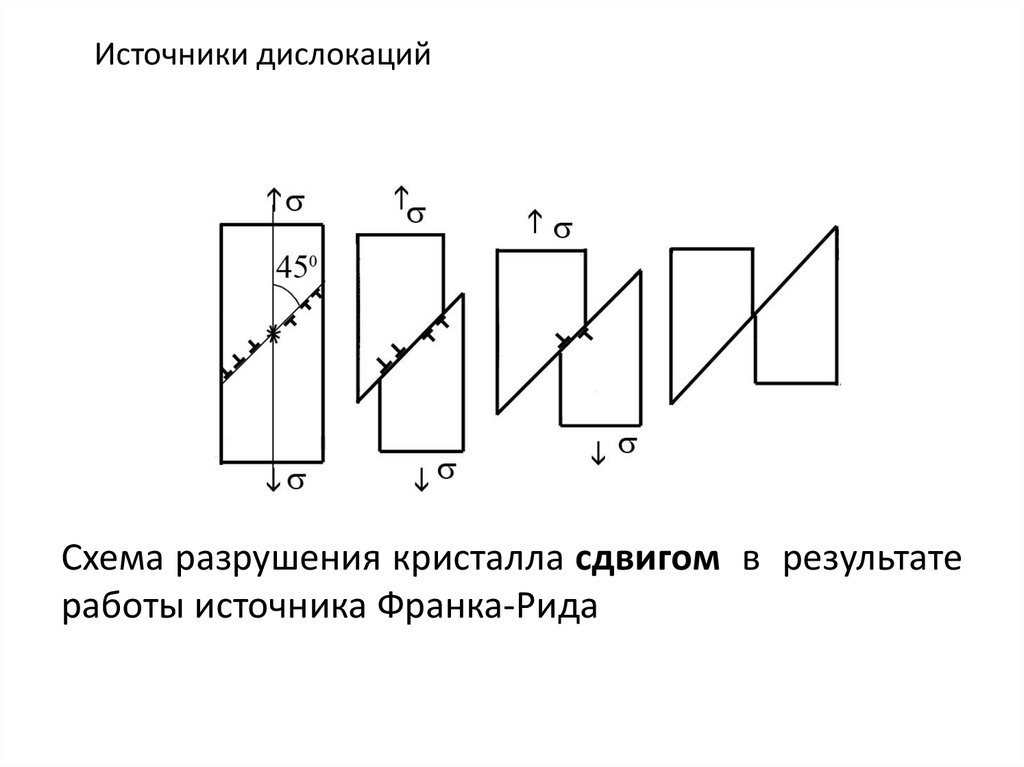
Источники дислокацийСхема разрушения кристалла сдвигом в результате
работы источника Франка-Рида
11.
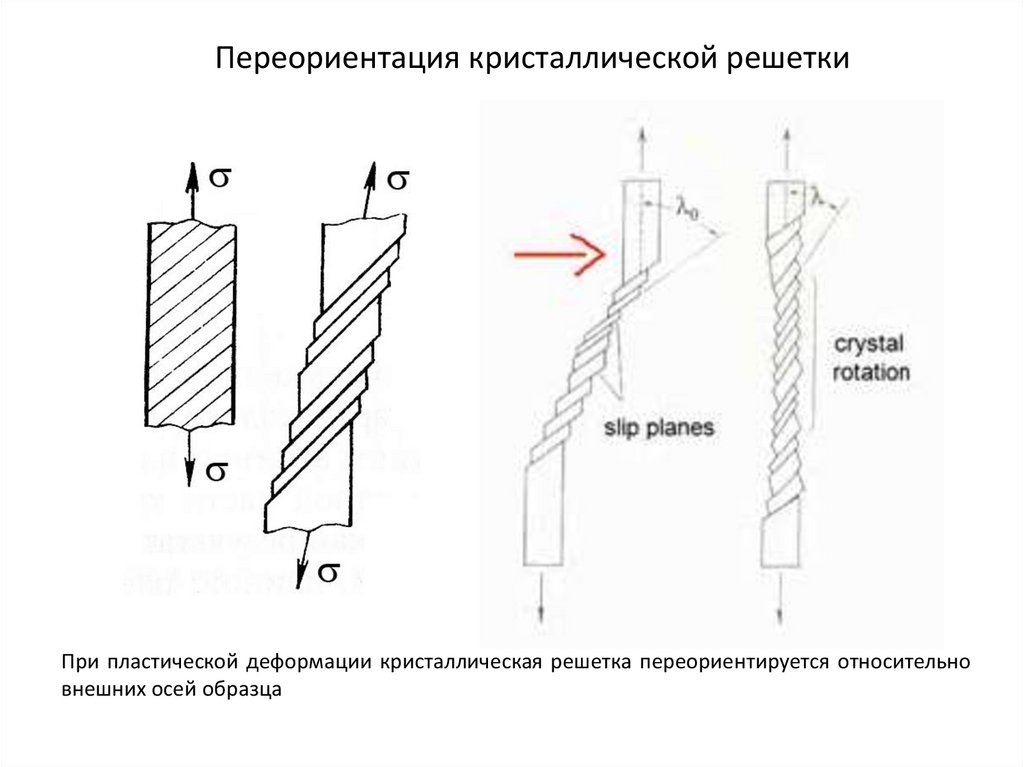
Переориентация кристаллической решеткиПри пластической деформации кристаллическая решетка переориентируется относительно
внешних осей образца
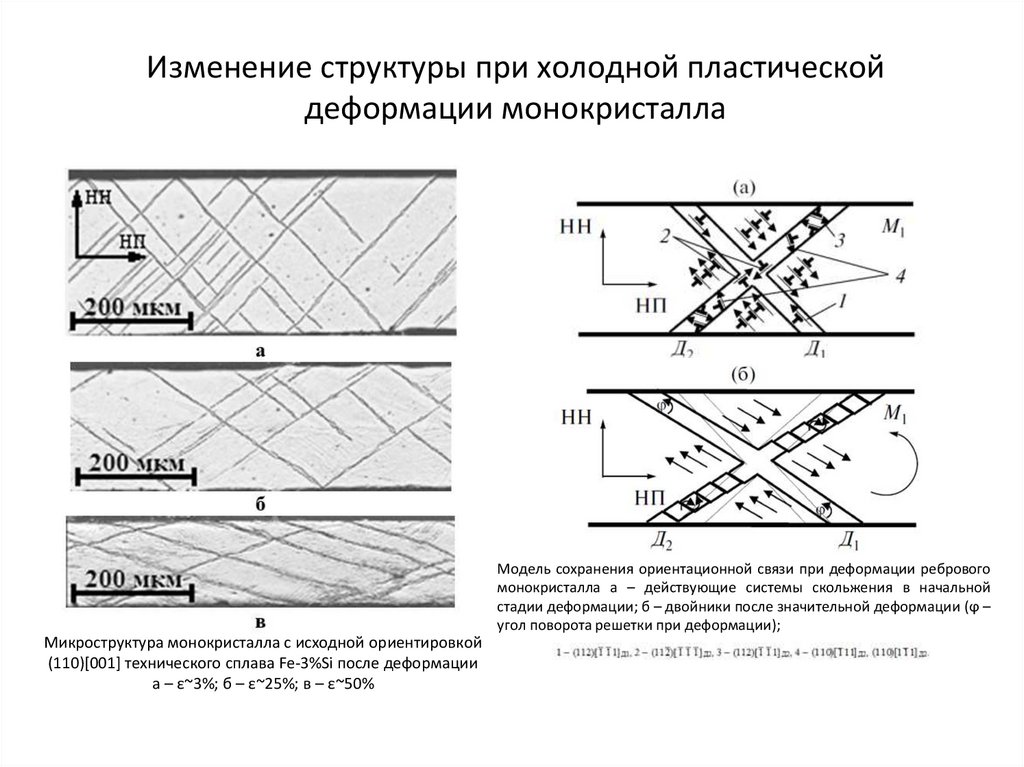
12. Изменение структуры при холодной пластической деформации монокристалла
Модель сохранения ориентационной связи при деформации ребровогомонокристалла а – действующие системы скольжения в начальной
стадии деформации; б – двойники после значительной деформации (ϕ –
угол поворота решетки при деформации);
Микроструктура монокристалла с исходной ориентировкой
(110)[001] технического сплава Fe-3%Si после деформации
а – ε~3%; б – ε~25%; в – ε~50%
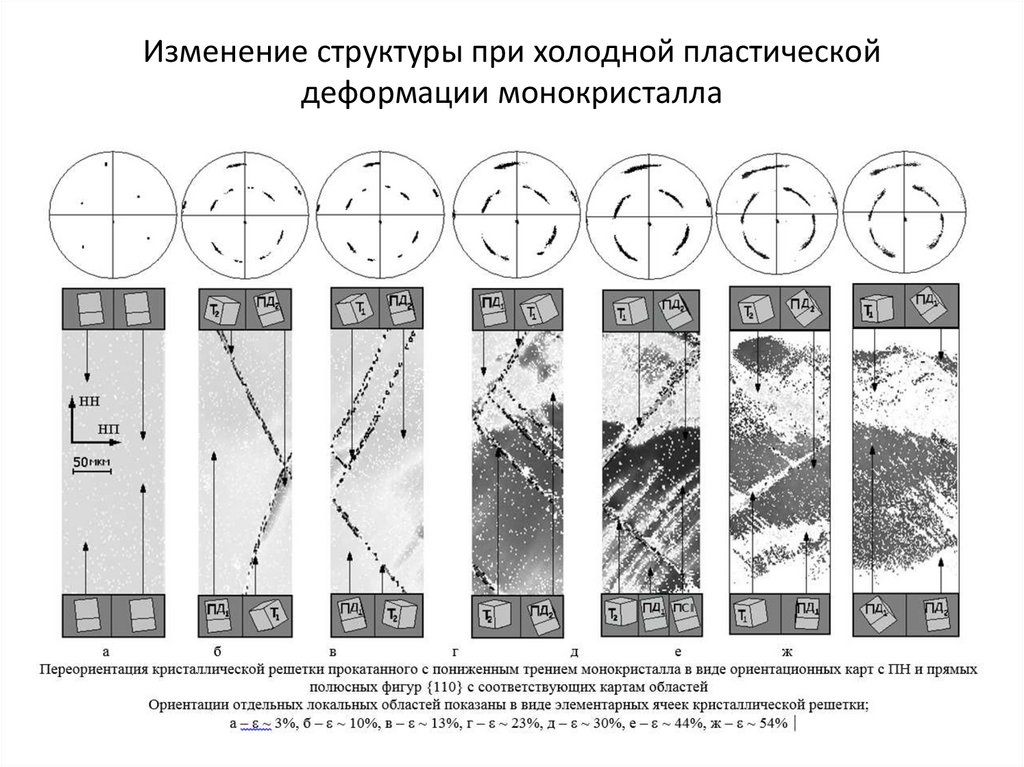
13. Изменение структуры при холодной пластической деформации монокристалла
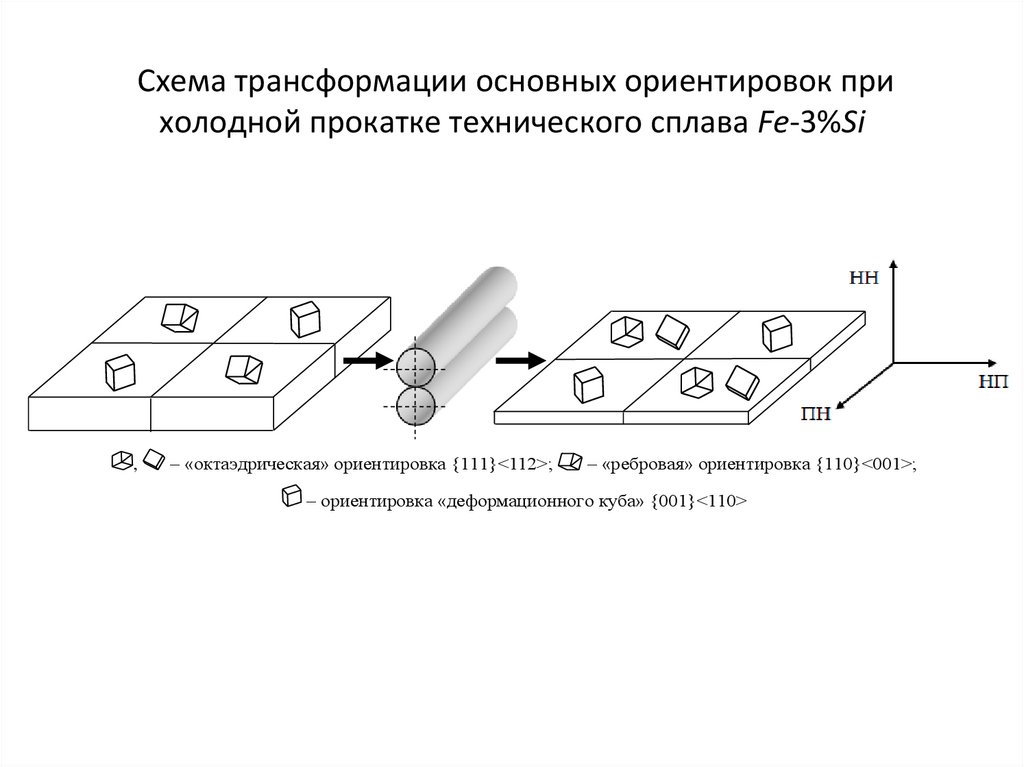
14. Схема трансформации основных ориентировок при холодной прокатке технического сплава Fe-3%Si
,– «октаэдрическая» ориентировка {111}<112>;
– «ребровая» ориентировка {110}<001>;
– ориентировка «деформационного куба» {001}<110>
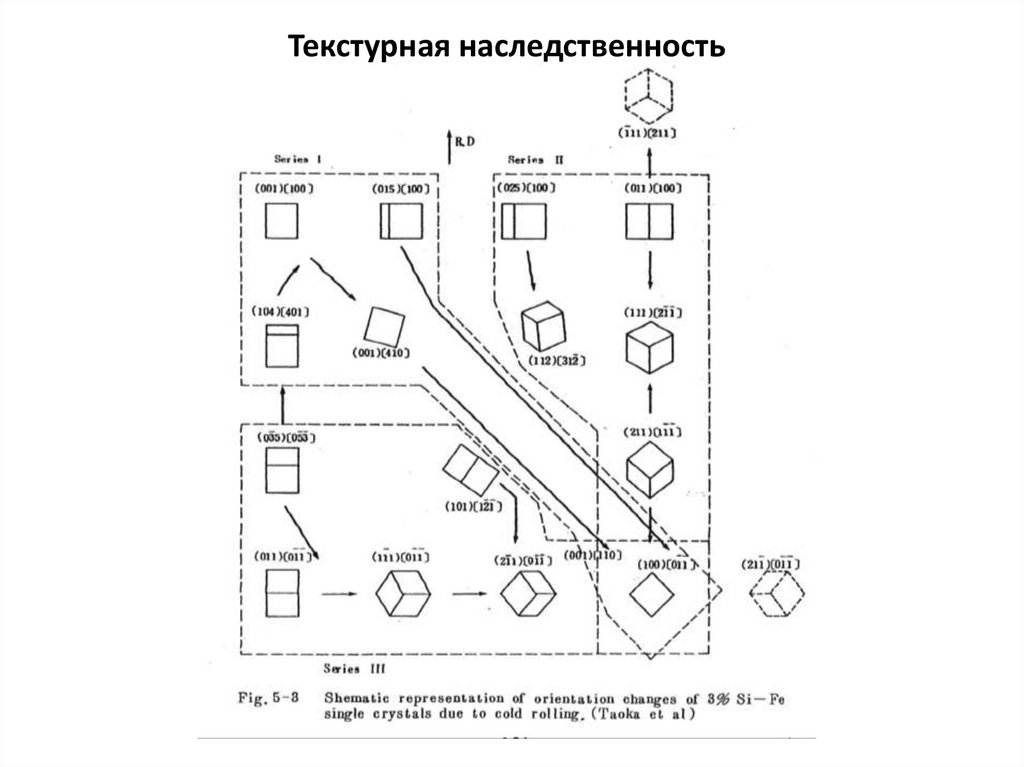
15.
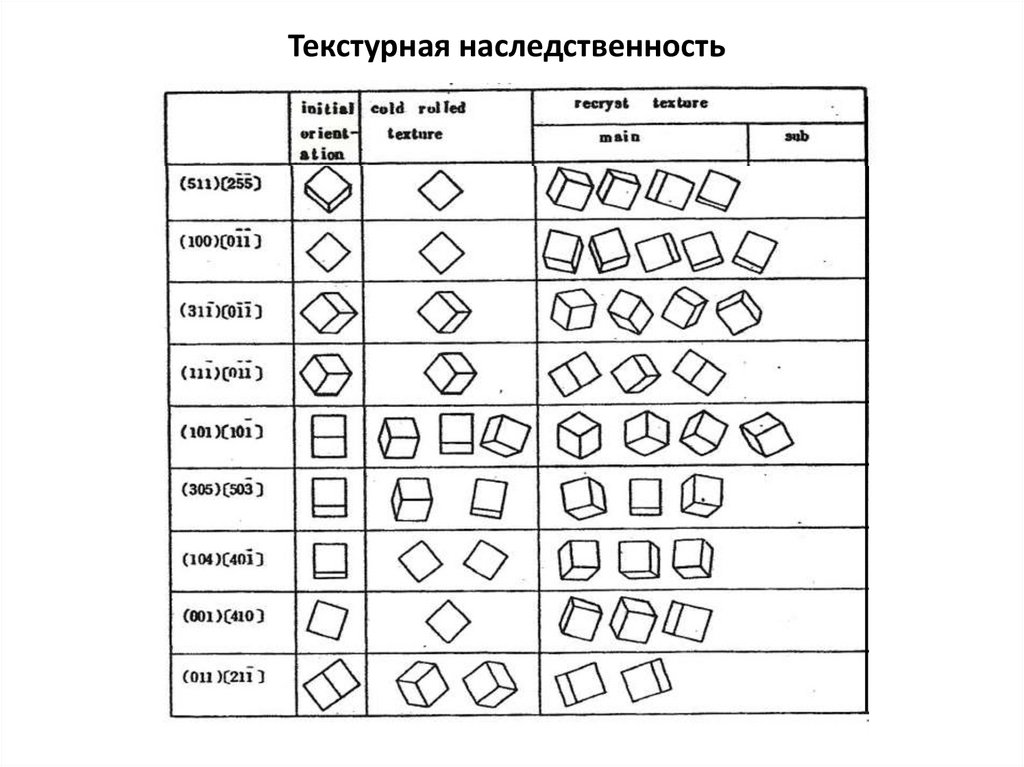
Текстурная наследственность16.
Текстурная наследственность17.
Текстурная наследственность18. Изменение структуры при холодной пластической деформации поликристаллов
Изменение микроструктуры поликристаллического материала придеформации: а – ɛ = 0 %; б – ɛ=1% ;в– ɛ=40%; г–ɛ=80% (продольное
сечение), д– ɛ=80% (поперечное сечение)
Плотность дислокаций:
Хорошо отожженный монокристалл – ρ ~ 104 см/см3
Рекристаллизованный металл – ρ ~ 105-106 см/см3
Деформированный металл – ρ ~ 1011-1012 см/см3
19.
20.
Пластическая деформация поликристалловМодель Закса:
- Все монокристаллические зерна в совокупности или поликристалл
испытывает одно и то же напряженное состояние;
- Условия равновесия по границам зерен удовлетворяются;
- Условия совместимости между зернами нарушенны, таким образом, что
конечные деформации приведут к пробелам и перекрытию между зернами
Модель Тейлора:
- Все зерна поликристалла испытывают одну и ту же деформацию
(деформации);
- Условие равновесия по границам зерен нарушены, так как вершинные
напряженные состояния, необходимые для активации множественного
скольжения в каждом зерне варьируются от зерна к зерну;
- Условия совместимости между зернами, удовлетворены
21.
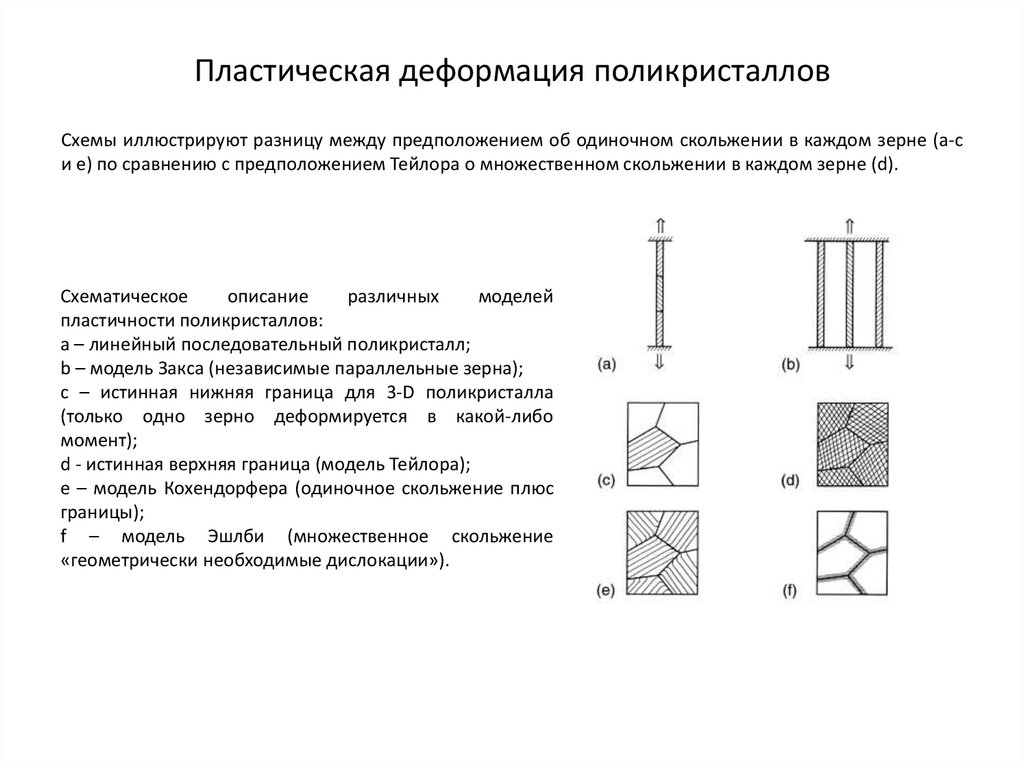
Пластическая деформация поликристалловСхемы иллюстрируют разницу между предположением об одиночном скольжении в каждом зерне (а-с
и е) по сравнению с предположением Тейлора о множественном скольжении в каждом зерне (d).
Схематическое
описание
различных
моделей
пластичности поликристаллов:
а – линейный последовательный поликристалл;
b – модель Закса (независимые параллельные зерна);
с – истинная нижняя граница для 3-D поликристалла
(только одно зерно деформируется в какой-либо
момент);
d - истинная верхняя граница (модель Тейлора);
е – модель Кохендорфера (одиночное скольжение плюс
границы);
f – модель Эшлби (множественное скольжение
«геометрически необходимые дислокации»).
22.
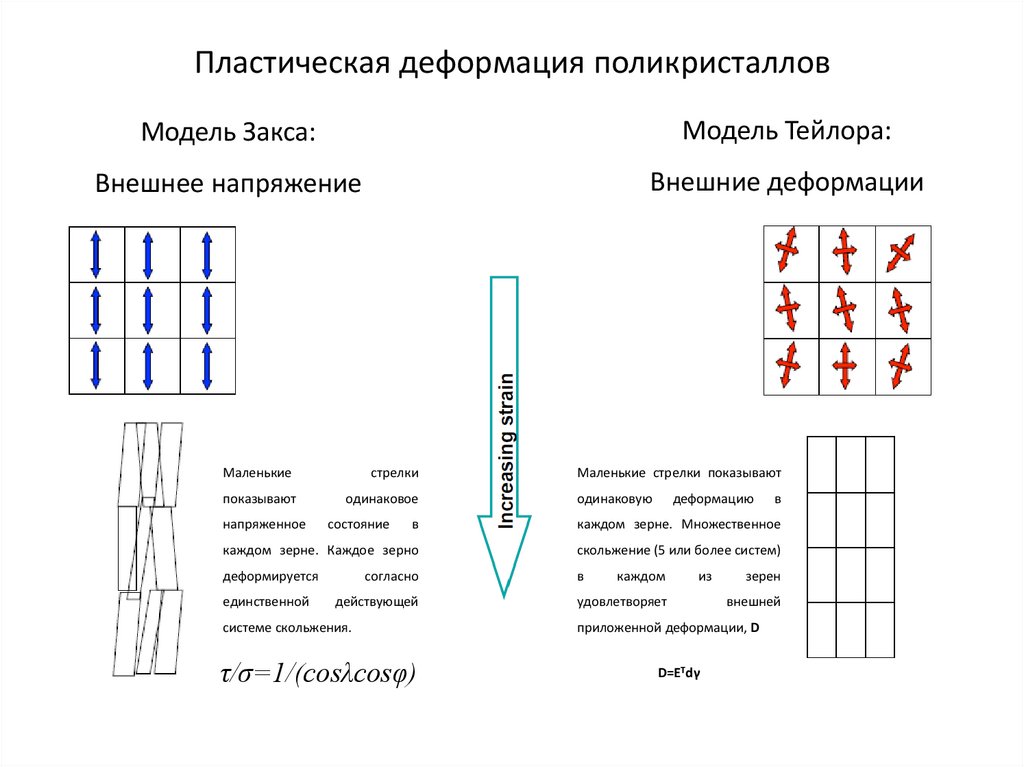
Пластическая деформация поликристалловМодель Закса:
Модель Тейлора:
Внешнее напряжение
Внешние деформации
Маленькие
стрелки
показывают
одинаковое
напряженное
одинаковую
деформацию
в
в
каждом зерне. Множественное
каждом зерне. Каждое зерно
скольжение (5 или более систем)
деформируется
в
единственной
состояние
Маленькие стрелки показывают
согласно
действующей
системе скольжения.
τ/σ=1/(cosλcosφ)
каждом
из
удовлетворяет
зерен
внешней
приложенной деформации, D
D=ETdγ
23.
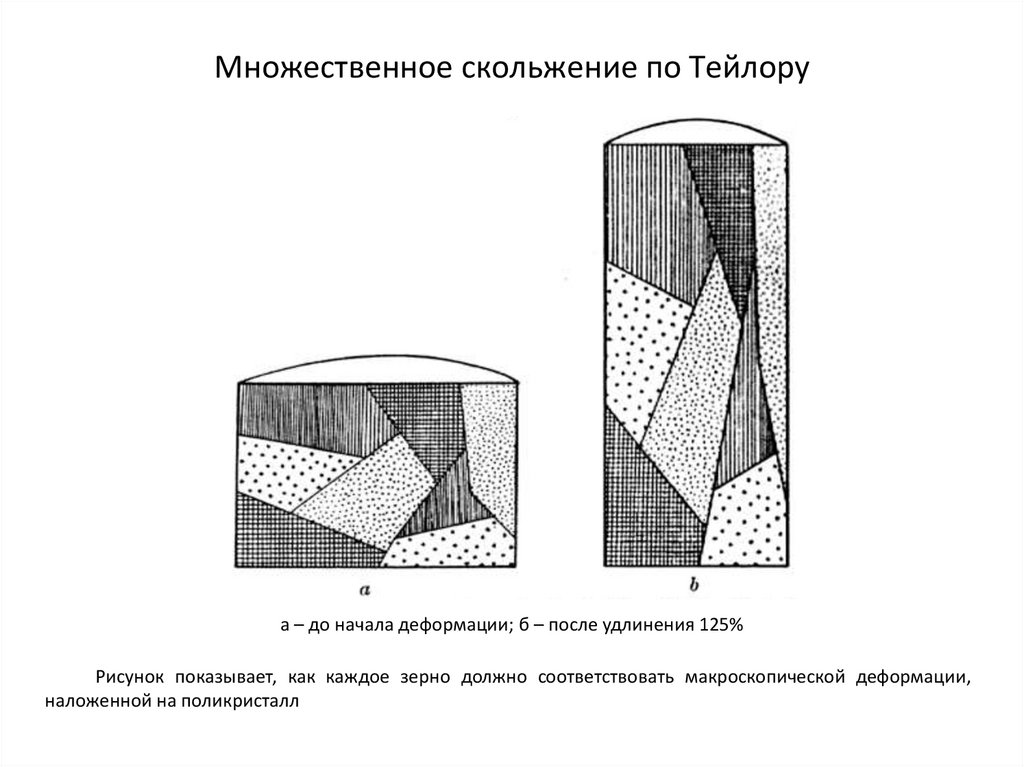
Множественное скольжение по Тейлоруа – до начала деформации; б – после удлинения 125%
Рисунок показывает, как каждое зерно должно соответствовать макроскопической деформации,
наложенной на поликристалл
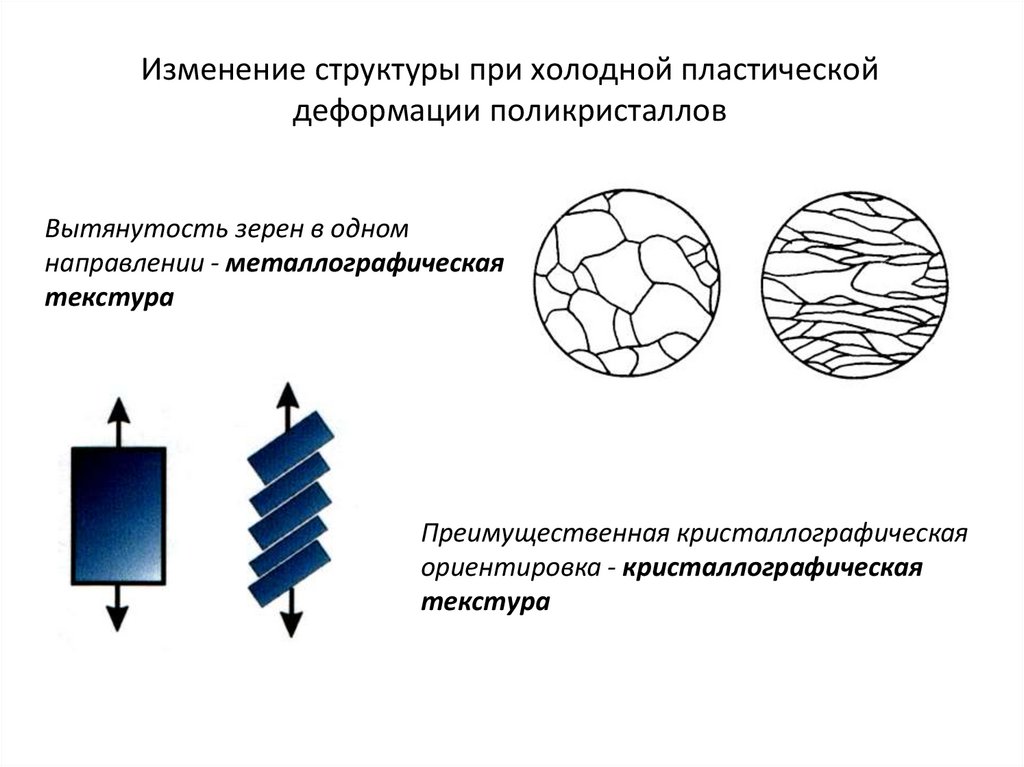
24. Изменение структуры при холодной пластической деформации поликристаллов
Вытянутость зерен в одномнаправлении - металлографическая
текстура
Преимущественная кристаллографическая
ориентировка - кристаллографическая
текстура
25.
Локализация деформации в микроструктуремикрополосы
а - микрополосы в хладнокатаной на 18% меди; б - микрополосы в холоднокатаной на 98%
меди; в - полосы сдвига холоднокатанной на 83% меди; г - деформированные двойники в
холоднокатаной на 30 %; д - следы деформации в латуни после сжатия на 14%
26.
Локализация деформации в микроструктуре (полосысдвига)
Мезоструктура деформированного
поликристалла (ε≈88%)
НН
НП
Структура деформированного кристалла
(110)[001] (ε≈89%)*
В поликристаллической ЭАС единственным
элементом
мезоструктуры,
содержащим
ребровую ориентировку являются полосы
сдвига.
1. Полоса сдвига в кристалле октаэдрической
ориентировки {111}<112> содержит дискретный набор
ориентаций кристаллической решётки. Анализ
показывает, что в полосах сдвига в заметном
количестве присутствуют две ориентации: {110}<001> и
{111}<112> (симметричная по отношению к матричной
{111}<112>).
2. Следы полос сдвига не являются следами плоскостей
скольжения или двойникования.
3. При пересечении двойника полосой сдвига в ней
обнаруживается сдвиговая компонента деформации
(γ≈2.0…2.9).
*D. Dorner, S. Zaefferer, D. Raabe. Retention of the Goss orientation between
microbands during cold rolling of an Fe3%Si single crystal // Acta mater. 2007. V.55. P.
2519…2530.
27.
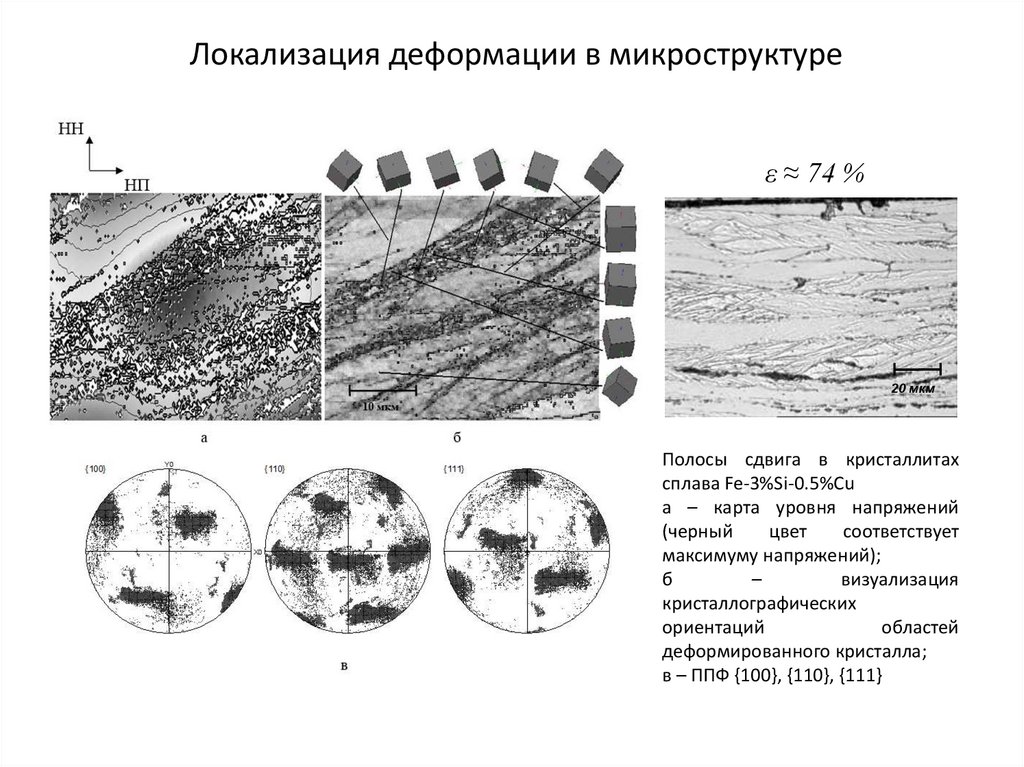
Локализация деформации в микроструктуреε ≈ 74 %
20 мкм
Полосы сдвига в кристаллитах
сплава Fe-3%Si-0.5%Сu
а – карта уровня напряжений
(черный
цвет
соответствует
максимуму напряжений);
б
–
визуализация
кристаллографических
ориентаций
областей
деформированного кристалла;
в – ППФ {100}, {110}, {111}
28. ПРОЦЕССЫ, ПРОТЕКАЮЩИЕ ПРИ НАГРЕВЕ ДЕФОРМИРОВАННОГО МЕТАЛЛА
1. Возврат1.1 Отдых
1.2 Полигонизация
2. Рекристаллизация
2.1 Первичная рекристаллизация (ПР)
2.2 Собирательной рекристаллизации или нормальный рост зерен (НР).
2.3 Вторичная рекристаллизация (ВР) или аномальный рост зерен.
29.
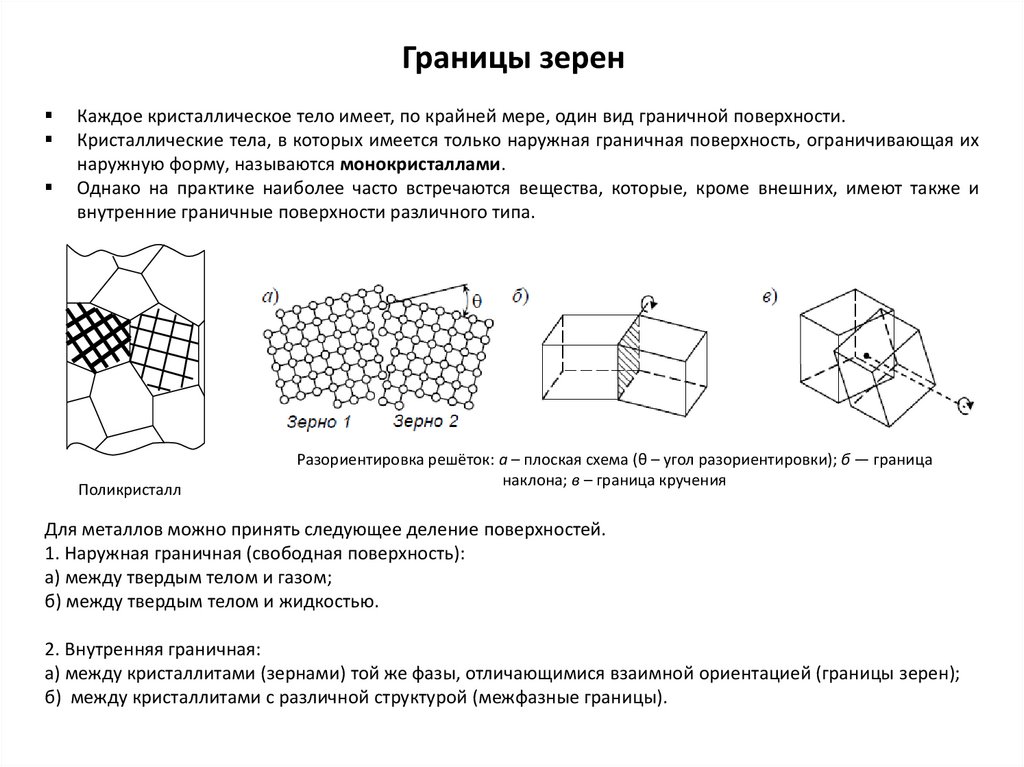
Границы зеренКаждое кристаллическое тело имеет, по крайней мере, один вид граничной поверхности.
Кристаллические тела, в которых имеется только наружная граничная поверхность, ограничивающая их
наружную форму, называются монокристаллами.
Однако на практике наиболее часто встречаются вещества, которые, кроме внешних, имеют также и
внутренние граничные поверхности различного типа.
Поликристалл
Разориентировка решёток: а – плоская схема (θ – угол разориентировки); б — граница
наклона; в – граница кручения
Для металлов можно принять следующее деление поверхностей.
1. Наружная граничная (свободная поверхность):
а) между твердым телом и газом;
б) между твердым телом и жидкостью.
2. Внутренняя граничная:
а) между кристаллитами (зернами) той же фазы, отличающимися взаимной ориентацией (границы зерен);
б) между кристаллитами с различной структурой (межфазные границы).
30.
Границы зеренРассмотрим границы между зернами одной фазы.
Граница зерна – это узкая ((2-3)а) зона между двумя соседними кристаллитами.
Различают границы:
- высокоугловые (большеугловые, БУГ)
- малоугловые (< 7-10º).
Такое деление принято в силу следующего обстоятельства: при разориентировке > 10° ядра дислокаций
образующих границы сливаются и для описания такой границы не пригодна дислокационная модель
(θ=b/h).
Свойства большеугловых границ:
1. БУГ перемещается диффузией;
2. Диффузия по БУГ при средних температурах идет значительно интенсивней, чем в объеме металла.
3. При повышенных температурах зерна могут смещаться относительно друг друга по границам
(межзеренное скольжение).
4. БУГ, как правило, обогащены примесными атомами.
5. Границы являются источниками и стоками вакансий, и дислокаций. Зависимость энергии БУГ от угла
разориентации не монотонна.
31.
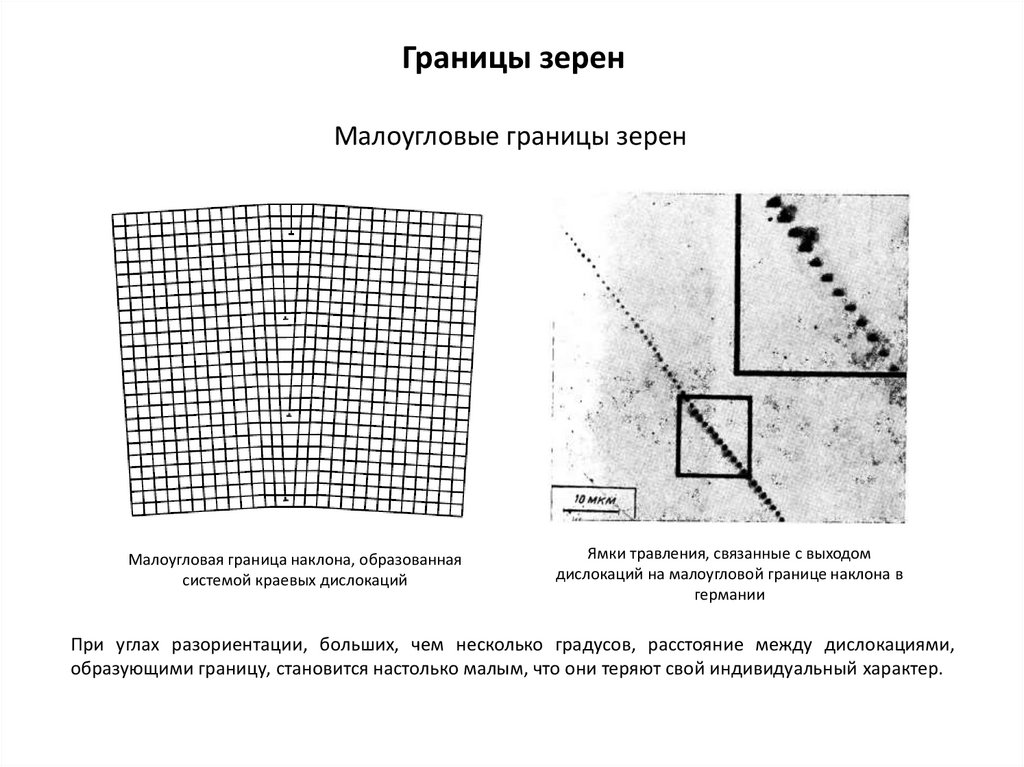
Границы зеренМалоугловые границы зерен
Малоугловая граница наклона, образованная
системой краевых дислокаций
Ямки травления, связанные с выходом
дислокаций на малоугловой границе наклона в
германии
При углах разориентации, больших, чем несколько градусов, расстояние между дислокациями,
образующими границу, становится настолько малым, что они теряют свой индивидуальный характер.
32.
Границы зеренЗависимость энергии симметричной границы вращения вокруг <110> для алюминия от угла наклона Θ.
Индексы приведенные на рисунке соответствуют индексам Миллера плоскостей границ
33.
Границы зеренМодель мест совпадения (специальные границы)
Если решетки двух кристаллов представить
взаимопроникающими и совмещенными в
некотором общем узле, то при некоторых
относительных
поворотах
возникает
трехмерная решетка совпадающих узлов
(РСУ).
Отношение объемов элементарных ячеек РСУ
и
исходной
решетки
характеризуется
параметром Σ – обратной пространственной
плотностью совпадающих узлов.
Схема расположения атомов в двойнике (111) в ГЦКрешётке. Граница двойника имеет тип Σ3 — совпадает
положение каждого третьего узла
Разориентировки, для которых Σ не слишком велика
(Σ<100÷150), получили название «специальных», если к
тому же плоскость границы может быть проведена через
совпадающие узлы, «специальной» называется и сама
граница. Характер совпадения в плоскости границы
зависит от ее ориентации относительно РСУ.
34.
Границы зеренМодель структурных единиц
Полиэдры
отражают
характерные
структуры
межзеренных границ и могут рассматриваться как
структурные
единицы.
Данные компьютерных
расчетов показывают, что самые низкоэнергетические
границы состоят из полиэдров только одного типа
(концепция мест совпадения). Если немного изменить
соотношение ориентаций, в структуре границ
появляются полиэдры других типов, которые
идентичны
областям
дислокаций.
С
ростом
рассогласования плотность новых структурных единиц
возрастает, пока они не становятся преобладающими
и при дальнейшем вращении граница опять не будет
состоять из полиэдров только одного типа. Концепция
структурных единиц и зависимость их структуры от
угла
разориентации
отражает
современные
представления о межзеренных границах.
Семь различных вариантов полиэдров Бернала, с помощью которых можно описать структуру
межзеренных границ в модели жестких сфер: а – тетраэдр; б – октаэдр; в – тригональная призма; г –
трехшапочная тригональная призма; д – квадратная (архимедова) антипризма; е – двухшапочная
архимедова антипризма; ж – пентагональная бипирамида
35.
ВозвратСовокупность любых процессов изменения и плотности дефектов в
деформированных кристаллах до начала рекристаллизации называют
возвратом.
Если возврат протекает без образования и миграции субграниц внутри
деформированных зерен, то его называют возвратом первого рода, или
отдыхом.
Схема изменения физических свойств при отдыхе, где линия 1 –
скорость отдыха, а линия 2 – изменение свойств
36.
ВозвратЕсли же при возврате внутри деформированных кристаллитов формируются и мигрируют малоугловые
границы, то его называют возвратом второго рода, или полигонизацией.
Процесс
полигонизации
заключается
в
перераспределении
дислокаций
(скольжением
или
переползанием) с формированием субзерен, отделенных друг от друга стенками малоугловых границ,
состоящих из краевых и винтовых дислокаций. Области кристалла, отделенные малоугловыми границами
и свободные от дислокаций, представляют собой блоки или полигоны.
Дислокационный механизм полигонизации описывается на примере деформированного изгибом
монокристалла, содержащего избыточное число краевых дислокаций одного знака. При отжиге
дислокации перегруппировываются и частично аннигилируют. Избыточные дислокации одного знака,
движимые упругим взаимодействием, образуют границы («стенки»), перпендикулярные плоскости
скольжения и не обладающие дальнодействующими полями напряжений.
Схема распределения дислокаций в деформированном изгибом кристалле до – а и после –
б полигонизации
37.
Формирование субзеренной структуры на стадииполигонизации
Границы субзерен
Границы субзерен
Ямки травления
а – начало формирования субзеренной структуры; б – субзеренная
структура; в – границы субзерен после небольших степеней
деформации, выявленные ямками травления
38.
Схема срастания соседних малоугловых границ,приводящего к укрупнению субзерен
Стрелками показаны направления, по которым должны смещаться
(путем сочетания процессов скольжения и переползания) дислокации,
участвующие в слиянии границ Р’, Р’’.
39.
Стадии коалесценции двух субзерен:а – исчезновение границы между субзернами; б – структура до коалесценции; в – поворот одного субзерна
относительно другого; г – структура после коалесценции; д – структура после выпрямления субграниц
вследствие миграции
40.
РекристаллизацияПроцесс зарождения и роста новых зерен в поликристаллическом
металле или сплаве при нагреве за счет других зерен той же фазы.
Субзеренная структура меди, содеражащая
дисперсионные частицы SiO2
41.
РекристаллизацияРекристаллизацию можно определить как миграцию большеугловых границ зерен (с большим углом
разориентации).
Границы будут двигаться, если при этом уменьшается свободная энергия системы (энергия Гиббса).
На рисунке схематически показан цилиндрический образец поперечного сечения F и длины L,
состоящей из двух частей I и II. Область I представляет собой свободное от деформации зерно. Область II – это
остальная часть образца, она может быть поликристаллом (деформированным или отожженным) или
монокристаллом другой ориентации. Области I и II разделены границей зерен, расположенной в позиции x.
Пусть gI и gII – свободные энергии единицы объема двух этих областей. Полную свободную энергию
системы тогда можно записать в виде:
Gtot= F [xgI + (L-x) gII].
I
(1)
II
x
L
Если gI > gII, то граница стремиться двигаться вправо. Это движение можно интерпретировать как
результат действия на границу «движущей силы» р, величина которой определяется формулой:
p = – 1/F (dGtot/dx) = gI – gII = Δg.
(2)
42.
РекристаллизацияЕсли gI и gII, даны в Дж/см3, то можно считать, что р=Δp H/см2 (104 Па). Такие «силы» не могут быть
непосредственно измерены. Граница – это не механическое тело, на которое могут действовать
внешние силы. Однако, абстракция, содержащаяся в уравнении (2) является общепринятой и будет
использоваться далее.
Существует несколько путей уменьшения свободной энергии системы при движении границы зерен,
каждый из которых вносит свой вклад pi в движущую силу. Как будет показано ниже, некоторые из
сил pi могут противодействовать движению границы «вперед», и тогда они выступают в роли
тормозящих сил. Однако все силы действуют в направлении, нормальном плоскости границы зерен.
Результирующая движущая сила составляет:
p = Σpi
(3)
v=mp,
(3а)
и граница будет двигаться со скоростью
где m – называется подвижностью границы.
[1] Рекристаллизация металлических материалов / Под ред. Ф. Хесснера. Пер. с англ.// М.: Металлургия. 1982. 352C.
43.
Первичная рекристаллизацияПервичная рекристаллизация (ПР) – появление и рост новых зерен с
пониженной плотностью дефектов при миграции исходных или новых
ВУГ.
Движущая сила ПР – уменьшение упругой энергии деформации
(связана с упругими полями дислокаций).
Энергия, запасенная при холодной деформации
Линейная энергия дислокаций равна примерно Gb2 (где G – модуль сдвига; b – вектор Бюргерса). Пусть ρI и ρ –
плотность дислокаций соответственно в областях I и II (рис), тогда результирующая движущая сила
p1=Gb2(ρ – ρI).
(4)
Если область I представляет собой рекристаллизованное зерно, а область II – деформированную матрицу, то ρ >> ρI, и
p1≈ ρGb2.
(5)
В действительности р1 зависит также от расположения дислокаций. Полигонизованный кристалл должен иметь более
низкую свободную энергию, чем просто деформированный кристалл с той же плотностью дислокаций (к тому же плотность
дислокаций обычно уменьшается в процессе отжига, приводящего к полигонизации). Так как эти изменения не влияют на
порядок величины р, здесь они учитываться не будут.
Пример. При Gb2 ≈ 10-8 Н плотность дислокаций, соответствующая холоднокатаному металлу (ρ ≈ 1012 см/см3),
создает движущую силу порядка 104 Н/см2 (108 Па), которая является движущей силой первичной рекристаллизации.
44.
Неоднородность микроструктуры к концу первичной рекристаллизациипосле холодной (а) и горячей (б) деформации
Схематическое изображение наложения двух процессов (возврата и
рекристаллизации) при изотермическом выделении накопленной энергии
45.
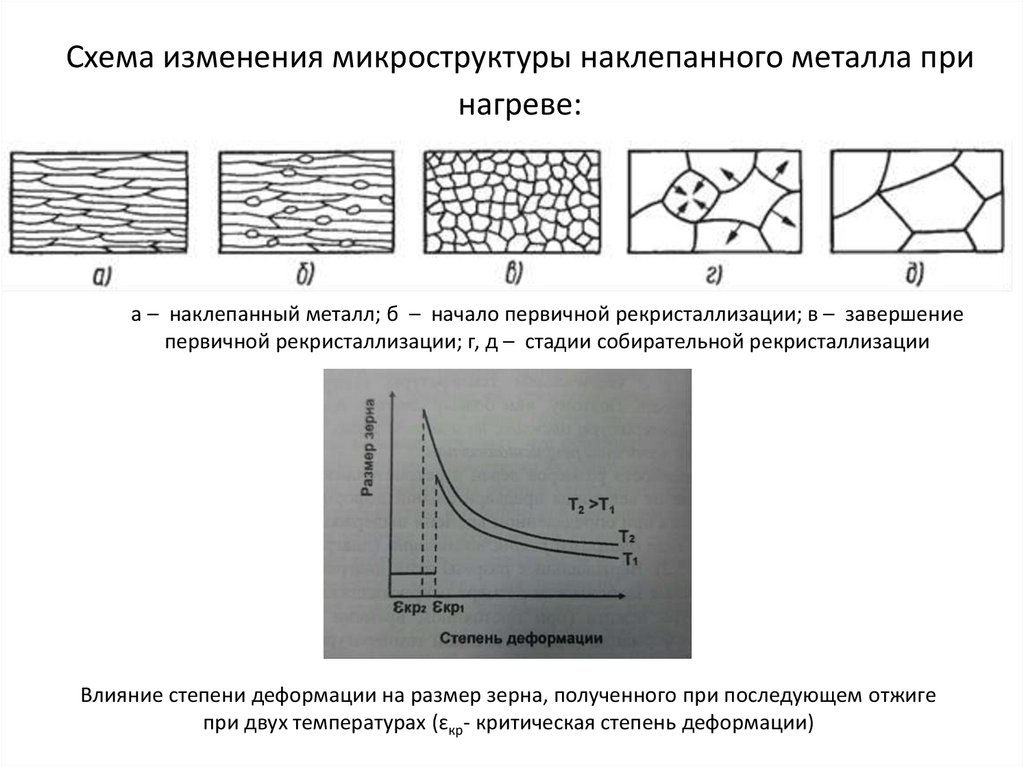
Схема изменения микроструктуры наклепанного металла принагреве:
а – наклепанный металл; б – начало первичной рекристаллизации; в – завершение
первичной рекристаллизации; г, д – стадии собирательной рекристаллизации
Влияние степени деформации на размер зерна, полученного при последующем отжиге
при двух температурах (ɛкр- критическая степень деформации)
46.
Собирательная рекристаллизацияПосле ПР материал обладает еще избыточной энергией связанной с
границами зерен.
При Собирательной рекристаллизации (НР) – происходит укрупнение
зерен, что приводит к уменьшению протяженности границ, т.е
уменьшение избыточной поверхности.
Движущая сила НР – уменьшение избыточной поверхностной энергии.
Энергия границ зерен
Пусть область I на рисунке 1 представляет собой большое зерно, растущее за счет мелкозернистой
первичной матрицы с размером зерна D. В этом случае Δg возникает благодаря присутствию множества
границ зерен и связанной с ними удельной зернограничной энергии γB. Если представить усредненное зерно
кубом с ребром D, отделенным от каждого соседнего зерна границей, площадь которой равна D2, то
движущая сила составит:
p2=6D2γB/2D3=3γB/D.
(6)
Пример. При γB = 3∙10-5 Дж/см3 и D=0,1 мм получаем силу р2 ≈ 1 Н/см2 (104 Па), которая является
движущей силой для нормального роста зерен и вторичной рекристаллизации.
47.
Собирательная рекристаллизацияНормальный рост зерен
В уравнение (6) р2 была введена как движущая сила вторичной рекристаллизации. Она является также и движущей
силой нормального роста зерен. Скорость роста, таким образом, пропорциональна р2, что приводит к соотношению
dD/dT ~ 1/D или D ~ √t.
(25)
Соотношение (25) является хорошо известным выражением для
кинетики роста зерен. Каждая граница в отдельности, конечно «не
знает», каким образом ей двигаться, чтобы средний размер зерен
увеличивался.
Вместо этого она будет двигаться по направлению к своему центру
кривизны, определяемому из условия, что в равновесии три границы,
образующие ребро зерна, должны пересекаться под углами 120° между
собой (в предположении, что поверхностные энергии всех границ
одинаковы).
На рис. 6 приведены двумерные зерна, являющиеся примером
того, как эти условия приводят к огранке маленьких зерен (имеющих
мало граней) выпуклыми границами, а больших зерен (с многими
гранями) – вогнутыми, так что большие зерна имеют тенденцию роста за
счет маленьких.
Кривизна границ зерен выступает как способ «распределения»
локализованных движущих сил по площади границы.
Рис. 6
[1] Рекристаллизация металлических материалов / Под ред. Ф. Хесснера. Пер. с англ.// М.: Металлургия. 1982. 352C.
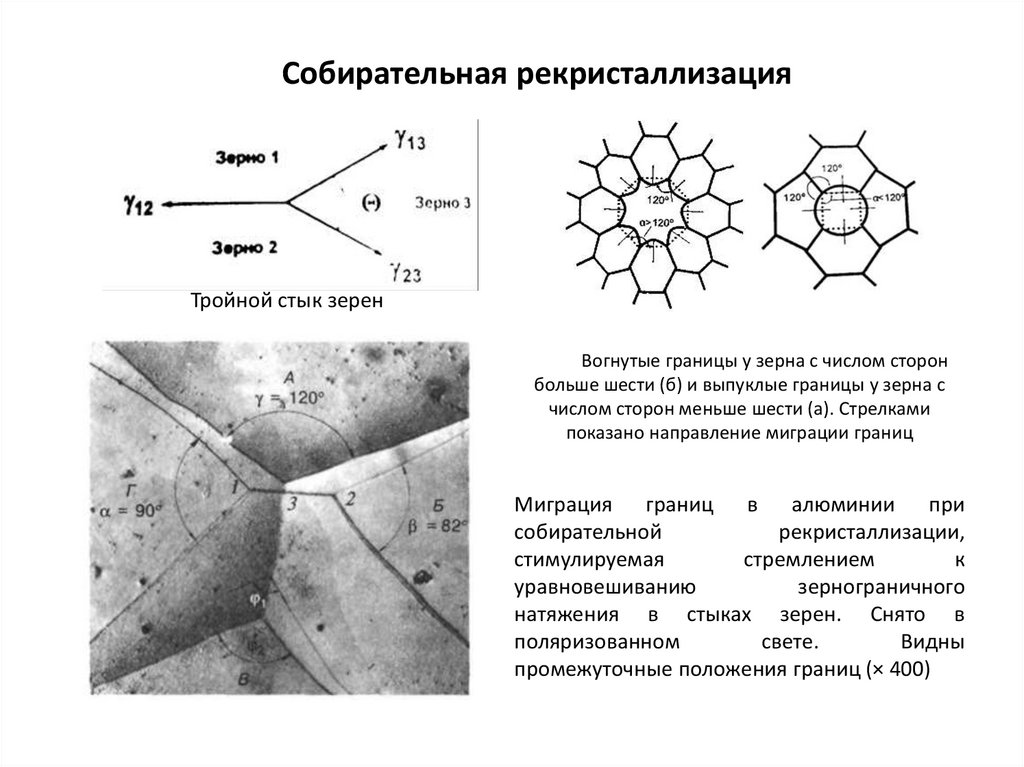
48.
Собирательная рекристаллизацияТройной стык зерен
Вогнутые границы у зерна с числом сторон
больше шести (б) и выпуклые границы у зерна с
числом сторон меньше шести (а). Стрелками
показано направление миграции границ
Миграция границ в алюминии при
собирательной
рекристаллизации,
стимулируемая
стремлением
к
уравновешиванию
зернограничного
натяжения в стыках зерен. Снято в
поляризованном
свете.
Видны
промежуточные положения границ (× 400)
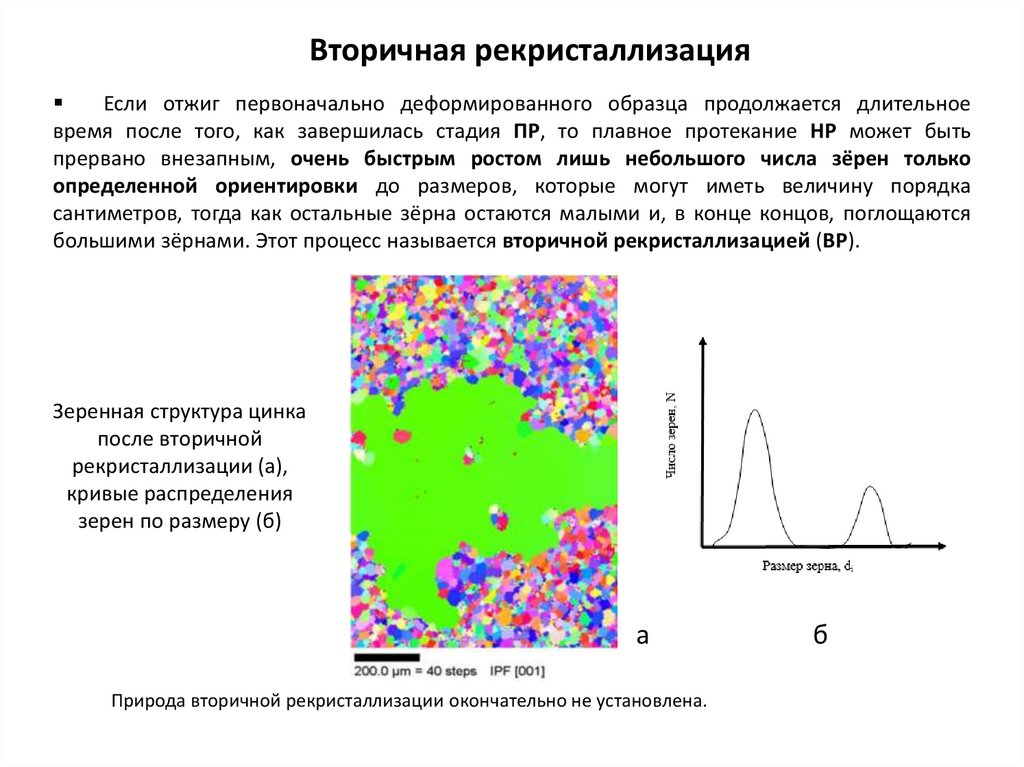
49.
Вторичная рекристаллизацияЕсли отжиг первоначально деформированного образца продолжается длительное
время после того, как завершилась стадия ПР, то плавное протекание НР может быть
прервано внезапным, очень быстрым ростом лишь небольшого числа зёрен только
определенной ориентировки до размеров, которые могут иметь величину порядка
сантиметров, тогда как остальные зёрна остаются малыми и, в конце концов, поглощаются
большими зёрнами. Этот процесс называется вторичной рекристаллизацией (ВР).
Зеренная структура цинка
после вторичной
рекристаллизации (а),
кривые распределения
зерен по размеру (б)
а
Природа вторичной рекристаллизации окончательно не установлена.
б
50.
Вторичная рекристаллизация1 Крупные зерна не являются вновь образованными, это просто выросшие до больших
размеров некоторые из образовавшихся при первичной рекристаллизации зерен.
2 Первые этапы роста больших зерен происходят медленно до того момента, как начнется
вторичная рекристаллизация; существует инкубационный период.
3 Наименее понятыми сторонами всего процесса являются факторы, управляющие отбором
зёрен-победителей, дорастающих до больших размеров, и механизмы, действующие на
первых этапах. Обычно считается, что выживающие при вторичной рекристаллизации зерна
должны заметно превосходить зерна среднего размера после первичной
рекристаллизации, и что они должны иметь ориентации, отличающиеся от
преимущественных в текстуре первичной рекристаллизации.
4 Какая-либо причина должна затруднить собирательную рекристаллизацию, так как только
при очень медленном росте зерен действительно могут вырасти очень крупные зерна за
счет вторичной рекристаллизации.
51.
Вторичная рекристаллизация5 По завершении вторичной рекристаллизации иногда формируется отчетливая текстура.
Она всегда отличается от предшествовавшей ей текстуры первичной рекристаллизации.
6 Для того, чтобы могла произойти вторичная рекристаллизация, должна быть превышена
некоторая четко определяемая минимальная температура. Обычно зерна наибольшего
размера получают как раз при температурах, несколько более высоких, чем этот порог, при
еще более высоких температурах вырастают более мелкие зерна.
7 Как только крупные зерна начали свой ускоренный рост, движущей силой вторичной
рекристаллизации обычно становится зернограничная энергия. В некоторых особых
условиях может влиять величина поверхностной энергии зерен на границе со средой
отжига.
52.
Вторичная рекристаллизацияОдним их основных условий для протекания процесса является
торможение нормального роста зёрен (так называемая “стабилизация
матрицы”), которое в принципе может осуществляться:
а) при наличии дисперсной неметаллической фазы (фазы-ингибитора);
б) в условиях осаждения (сегрегации) примесных атомов на границах
зёрен;
в) под воздействием канавок термического травления (эффект толщины);
г) в условиях текстурного торможения.
В промышленной трансформаторной стали стабилизация матрицы
осуществляется включениями второй фазы. Природа включений второй
фазы может быть самой различной: AlN, MnS, MnSe. Важно только, чтобы
при температуре окончательного отжига эта фаза была термически
нестабильной. В противном случае, как, например, при торможении
роста зерен стабильными включениями Аl2O3, ВР не протекает.
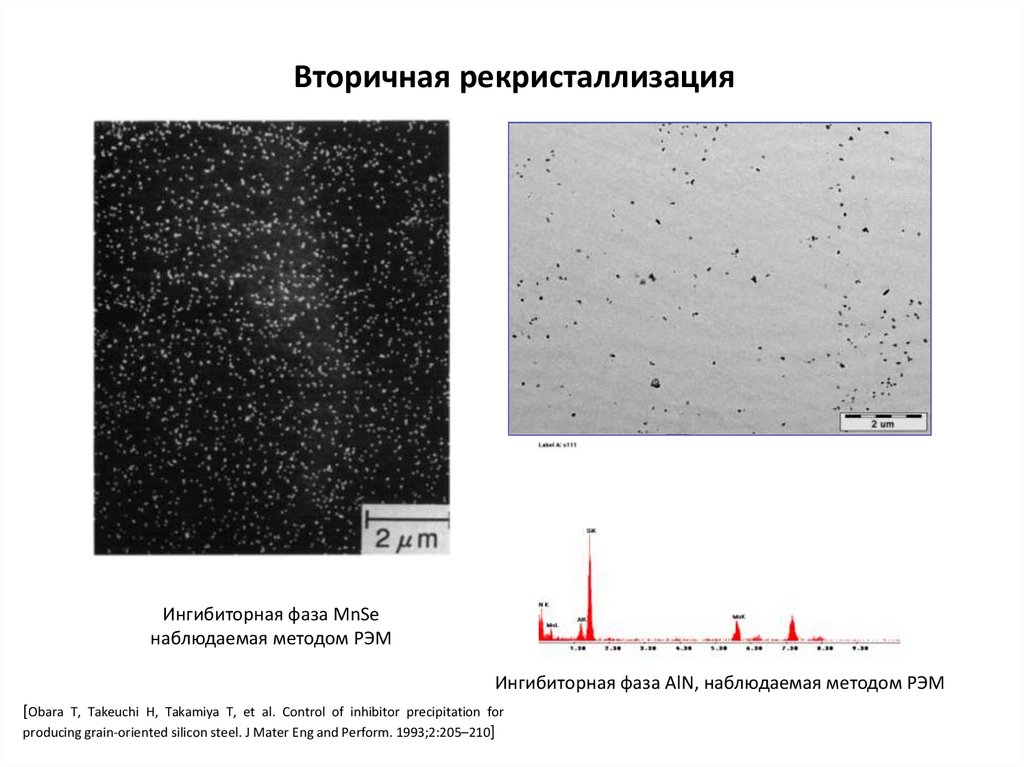
53.
Вторичная рекристаллизацияИнгибиторная фаза MnSe
наблюдаемая методом РЭМ
Ингибиторная фаза AlN, наблюдаемая методом РЭМ
[Obara T, Takeuchi H, Takamiya T, et al. Control of inhibitor precipitation for
producing grain-oriented silicon steel. J Mater Eng and Perform. 1993;2:205–210]
54.
Вторичная рекристаллизация900℃
950℃
1000℃
1050℃
1100℃
ND
100㎛
RD
Параметры ингибиторной фазы (AlN, MnS):
- объёмная доля ~ 0.015 %;
- количество частиц ~ 1012-1014 шт/см3;
- размер частиц < 1000 Å.
RD
TD
1 cм
ND – normal direction, TD – transverse direction, RD – rolling direction
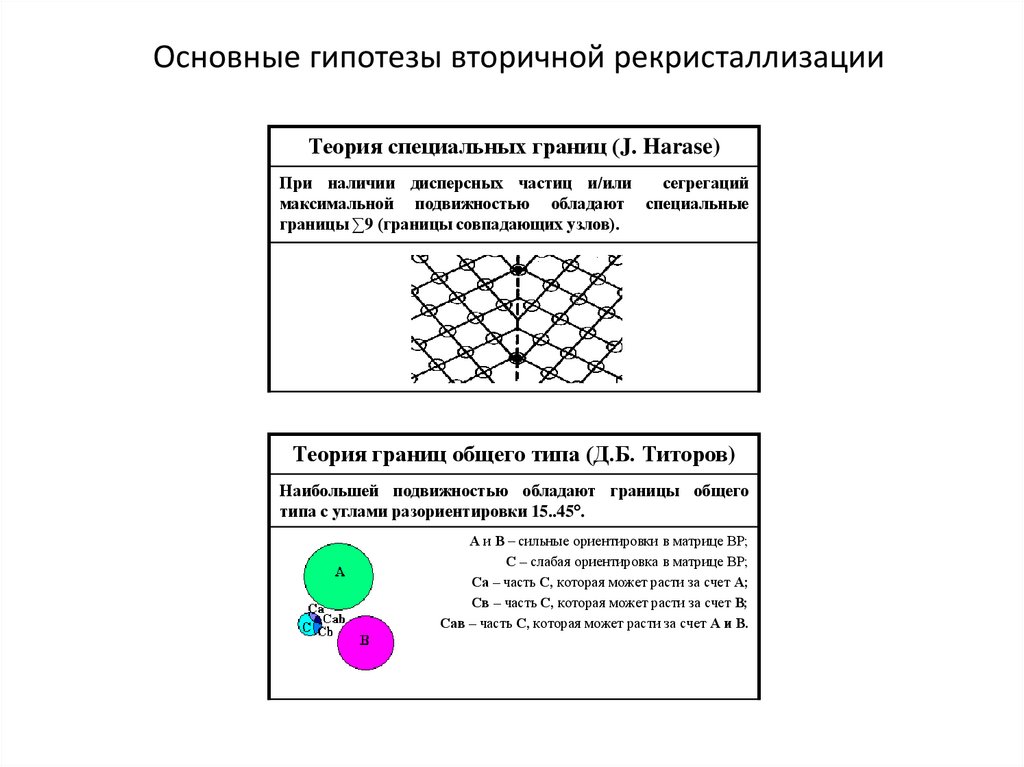
55.
Основные гипотезы вторичной рекристаллизацииТеория специальных границ (J. Harase)
При наличии дисперсных частиц и/или
сегрегаций
максимальной подвижностью обладают специальные
границы ∑9 (границы совпадающих узлов).
Теория границ общего типа (Д.Б. Титоров)
Наибольшей подвижностью обладают границы общего
типа с углами разориентировки 15..45 .
А и В – сильные ориентировки в матрице ВР;
С – слабая ориентировка в матрице ВР;
Са – часть С, которая может расти за счет А;
Св – часть С, которая может расти за счет В;
Сав – часть С, которая может расти за счет А и В.
56.
Вторичная рекристаллизация1.
Формирование
(110)[001] областей
ND
ребровых
Схематическое изображение поперечного сечения
листа ЭАС, показывающее зарождение и рост
вторичнорекристаллизованных зерен ребровой
ориентировки
RD
2. Деформированная структура с
ориентацией {111}<112>
3. Потенциальное формирование
зерен
(110)[001]
в
матрице
первичной рекристаллизации
4. Деформированная структура с
ориентацией {111}<112>
5.
Колонии
рекристаллизованных
(110)[001]
первичнозерен
ND – normal direction, TD – transverse direction, RD – rolling direction
[Inokuti Y. Preferential growth of secondary recrystallized Goss grains during secondary recrystallization annealing in grain oriented silicon steel sheet. Textures
Microstruct. 1996;26–27:413–426]
57.
Вторичная рекристаллизацияЗародыши ВР с ориентировкой {110}<001> возникают в листах
холоднокатаной стали в подповерхностных слоях на глубине ~ 1/10 …1/4
от толщины листа, как раз в тех местах, где оказывается усиленной
составляющая {111}<uvw> и уменьшенным размер зерна.
В средних слоях листа условия менее благоприятны для формирования
зародышей ВР.
Неоднородность микроструктуры и текстуры в холоднокатаном листе
электротехнической стали, приводящая к преимущественному
образованию зародышей ВР в подповерхностном слое, обусловлена
структурной и текстурной неоднородностью горячекатаной полосы. В
подповерхностном слое горячекатаной полосы также усилена
составляющая {110}<001> и уменьшен средний размер зерна.
58.
Структура и текстура подповерхностного слоя горячекатаногоподката технического сплава Fe-3%Si
НН
НП
• Известно, что в подповерхностных слоях полосы (~1/8 толщины) , где после горячей деформации была
усилена текстурная компонента (110)[001], в процессе холодной прокатки происходит образование
ориентировки {111}<112>
• Характерной особенностью зарождения центров вторичной рекристаллизации является то, что они
всегда возникают в подповерхностных слоях полосы (1/10…1/4 ее толщины)
59.
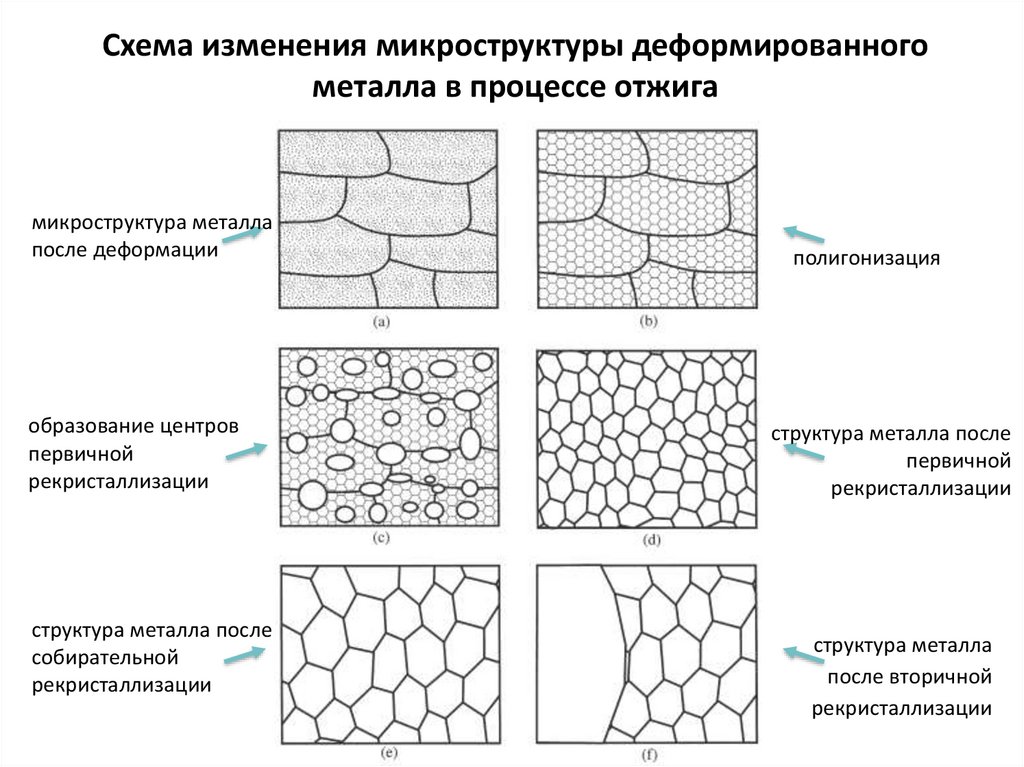
Схема изменения микроструктуры деформированногометалла в процессе отжига
микроструктура металла
после деформации
образование центров
первичной
рекристаллизации
структура металла после
собирательной
рекристаллизации
полигонизация
структура металла после
первичной
рекристаллизации
структура металла
после вторичной
рекристаллизации
60.
Движущие силы рекристаллизацииЭнергия, запасенная при холодной деформации
Линейная энергия дислокаций равна примерно Gb2 (где G – модуль сдвига; b – вектор Бюргерса). Пусть ρI и ρ – плотность
дислокаций соответственно в областях I и II (рис. 1), тогда результирующая движущая сила
p1=Gb2(ρ – ρI).
(4)
Если область I представляет собой рекристаллизованное зерно, а область II – деформированную матрицу, то ρ >> ρI, и
p1≈ ρGb2.
(5)
В действительности р1 зависит также от расположения дислокаций. Полигонизованный кристалл должен иметь более
низкую свободную энергию, чем просто деформированный кристалл с той же плотностью дислокаций (к тому же плотность
дислокаций обычно уменьшается в процессе отжига, приводящего к полигонизации). Так как эти изменения не влияют на
порядок величины р, здесь они учитываться не будут.
Н/см2
Пример. При Gb2 ≈ 10-8 Н плотность дислокаций, соответствующая холоднокатаному металлу (ρ ≈ 1012 см-2), создает движущую силу порядка 104
(108 Па), которая является движущей силой первичной рекристаллизации.
Энергия границ зерен
Пусть область I на рисунке 1 представляет собой большое вторичное зерно, растущее за счет мелкозернистой первичной
матрицы с размером зерна D. В этом случае Δg возникает благодаря присутствию множества границ зерен и связанной с ними
удельной зернограничной энергии γB. Если представить усредненное зерно кубом с ребром D, отделенным от каждого
соседнего зерна границей, площадь которой равна D2, то движущая сила составит:
p2=6D2γB/2D3=3γB/D.
(6)
Пример. При γB = 3∙10-5 Дж/см3 и D=0,1 мм получаем силу р2 ≈ 1 Н/см2 (104 Па), которая является движущей силой для нормального роста зерен и
вторичной рекристаллизации.
[1] Рекристаллизация металлических материалов / Под ред. Ф. Хесснера. Пер. с англ.// М.: Металлургия. 1982. 352C.
61.
Движущие силы рекристаллизации (2)Поверхностная энергия
Пусть образец на рисунке 1 представляет собой тонкую пластину, а области I и II являются монокристаллами. Если на
внешнюю поверхность будут выходить разные кристаллографические плоскости, то их удельные свободные поверхностные
энергии γs могут различаться. Это приводит к возникновению движущей силы:
p3=2Δγs/ω.
(7)
где ω – толщина пластины; Δγs – разность удельных поверхностных энергий. Для движения границ зерен, вызванного этой
движущей силой, был введен термин «третичная рекристаллизация». Величина разности удельных поверхностных энергий Δγs
определяется не только ориентацией двух кристаллов. Она зависит от атмосферы отжига. Изменяя состав атмосферы, можно
добиться изменения даже знака Δγs, так что граница зерен изменит направление движения на обратное.
Пример. Для Δγs ≈ 5∙10-6 Дж/см2 и ω=0,1 мм получаем р3≈0,1 Н/см2 (103 Па).
Магнитная энергия
Пусть образец на рис. 1 представляет собой бикристалл железа, помещенный в магнитное поле, причем в области I
направлению поля параллельна ось <100>, а в области II – <111>. Предположим, что образец находится при температуре ниже
точки Кюри, а поле является достаточно сильным, чтобы оба зерна были намагничены до насыщения. Различие в магнитных
энергиях приведет тогда к появлению движущей силы:
p4=0,00114∙Ws/1 см3 ≈ 0,1 Н/см2 (103 Па).
(8)
Это максимальное значение движущей силы, которого можно достичь в железе при помощи магнитного поля. Усиливая
магнитное поле, движущую силу увеличить нельзя. Однако она может быть меньше приведенного значения, если приложенное
поле недостаточно для магнитного насыщения материала или если ориентация обоих зерен отличается от указанных выше.
[1] Рекристаллизация металлических материалов / Под ред. Ф. Хесснера. Пер. с англ.// М.: Металлургия. 1982. 352C.
62.
Движущие силы рекристаллизации (3)Дисперсные выделения
Выделение дисперсных частиц обычно не рассматривается как рекристаллизационное явление. Однако, как и при
рекристаллизации, элементарным процессом здесь является движение большеугловых границ зерен. Перед движущейся
границей лежит пересыщенный твердый раствор, за ней находится более близкий к термодинамическому равновесию
двухфазный сплав. Разница в молярной свободной энергии, которую опять-таки можно считать движущей силой движения
границы, дается формулой:
Δg=(U/V)[C0(1-C0)-C1(1-C1)]+(RT1/V)×[C0lnC0-C1lnC1+(1-C0)ln(1-C0)-(1-C1)ln(1-C1)].
(9)
где V – молярный объем; C0 – концентрация сплава; Т1 – температура отжига; С1 – растворимость, соответствующая температуре
Т1. Для малых концентраций выражение (9) упрощается:
Δg ≈(U/V)(C0-C1)+(RT1/V)×(C0lnC0-C1lnC1).
(10)
Значение U можно оценить по уравнению кривой растворимости
С =exp(-U/RT).
(11)
Если ввести температуру Т0, при которой растворимость равна С0, то уравнение (10) принимает вид:
р5 =R(T1-Т0)C0lnC0.
(12)
Пример. При 779°C в меди можно растворить 4,9% (ат.) серебра и закалкой зафиксировать пересыщенный твердый раствор. В таком сплаве в
процессе отжига при 300°C будет идти выделение дисперсных частиц. Движущая сила для этого случая составляет 630 Дж/моль ≈ 6∙104 Н/см2 (6∙108 Па).
[1] Рекристаллизация металлических материалов / Под ред. Ф. Хесснера. Пер. с англ.// М.: Металлургия. 1982. 352C.
63.
Тормозящие силыС частицами второй фазы, растворенными атомами и поверхностными канавками термического травления, связаны
силы, тормозящие движение границ зерен. Однако на неподвижную границу эти силы не действуют. Так как по определению
сумма в уравнении (3) всегда положительна или равна нулю, то тормозящие силы могут частично или полностью
уравновешивать движущую силу.
Частицы второй фазы (зинеровское торможение)
На рисунке 2 изображена сферическая частица радиуса r, пересекающая плоскость границы зерен.
Зернограничная энергия при этом уменьшилась на величину πy2γB. В отсутствие движущих
сил граница находится в положении x=0, так как при этом уменьшение энергии максимально, а
сила взаимодействия границы с включением равна нулю. Если, однако, граница сдвинется под
действием некоторой движущей силы вправо, то со стороны частицы на нее начнет действовать
тормозящая сила. Пусть Z – число частиц, приходящихся на 1 см2 границы. Тогда эта сила равна
р7=Zd(πy2γB)/dx=-2Z γB πx.
(13)
r
y
x
Рис. 2
Сила р7 достигает максимума при x=r. Если f – объемная доля второй фазы, то Z – можно выразить как:
Z=f/πr2.
(14)
и максимальное значение тормозящей силы равно
р7=-2γB f/r.
Пример. При f=1%, радиусе r=5 мкм и γB ≈ 2,5∙10-5 Дж/см2. Тогда р7 ≈ -0,1 Н/см2.
[1] Рекристаллизация металлических материалов / Под ред. Ф. Хесснера. Пер. с англ.// М.: Металлургия. 1982. 352C.
(15)
64.
Тормозящие силы (2)Растворенные атомы
Если применить уравнение (15) к описанию тормозящих сил, действующих со стороны примесных атомов, то под f надо
понимать атомную концентрацию, а под величиной 2r – атомный диаметр. Тогда 1% (ат.) привел бы к возникновению
тормозящей силы р8 порядка 104 Н/см2 (108 Па). Качественно это разумный результат. Сравнение р1, р2, р7 и р8 ясно показывает,
что включения второй фазы могут влиять только на вторичную рекристаллизацию, тогда как растворенные примеси могут
влиять и на вторичную, и на первичную. Это согласуется с экспериментом.
Однако количественного согласия при таком распространении уравнения (15) ожидать не приходится, поскольку
примесные атомы не неподвижны (как частицы второй фазы), а могут перемещаться по решетке путем диффузии. Отсюда
следует два важных вывода.
Во-первых, существует энергия взаимодействия UB между растворенными атомами и границей зерен. Хотя UB трудно
рассчитать или измерить, различные оценки приводят к значениям порядка нескольких десятых электрон-вольт на атом.
Следовательно, концентрация примесных атомов в границе С превышает среднюю концентрацию С0:
С =exp(-UB/RT).
(16)
Это объясняет, почему примесь даже в концентрациях, составляющих стотысячные доли процента, может заметно
влиять на ход рекристаллизации. Вероятно, UB может быть отрицательной в определенных системах сплавов. Граница тогда
должна быть чище, чем кристалл. Вопреки ожиданиям, это мало меняет результаты теории.
Во-вторых, примесные атомы стремятся двигаться вместе с границей. В очень медленно движущейся границе они всегда
будут располагаться вблизи своего равновесного положения, и сколько-нибудь заметная тормозящая сила не возникает. По
этой причине растворенные атомы примеси не являются серьезной помехой вторичной рекристаллизации, хотя они могут
существенно замедлять первичную рекристаллизацию в той же системе.
Если же движущая сила очень велика (или концентрация примеси достаточно мала), то граница может оторваться от
своей примесной атмосферы и снова двигаться через кристалл почти беспрепятственно. Максимальное значение тормозящей
силы достигается, таким образом, в промежуточной области зернограничных скоростей.
Переход от «грязной» к «чистой» границе зависит от температуры. Следовательно, температурная зависимость
рекристаллизации является весьма сложной, и ее нельзя представить аррениусовской зависимостью с одной энергией
активации. Это объясняет большой разброс значений «энергии активации» рекристаллизации в литературе даже для сходных
металлов.
[1] Рекристаллизация металлических материалов / Под ред. Ф. Хесснера. Пер. с англ.// М.: Металлургия. 1982. 352C.
65.
Тормозящие силы (3)Канавки на внешней поверхности
Термическое травление приводит к образованию канавки на поверхности
металла в том месте, где на эту поверхность выходит граница зерен. Такая
канавка схематически показана на рис.3. Она характеризуется углом φ при
вершине, который определяется равенством
sinφ = γB / 2 γs.
(17)
Рис. 3
Если граница смещается по отношению к канавке, то она должна увеличить свою длину. Это приводит к появлению
тормозящей силы, пропорциональной γB и tgφ. Когда образец представляет собой тонкую пластину, граница пронизывает его
на всю толщину ω. При этом такая сила возникает на обеих сторонах пластины. Поскольку угол φ мал, то
р9= γB2 / ωγs.
(18)
Следует отметить, что тормозящая сила зависит только от угла φ и не зависит от глубины канавки. Таким образом,
канавка порождает тормозящую силу, даже если она еще невидима. Формула (18) позволяет оценить максимально возможное
значение тормозящей силы, когда граница уже готова оторваться от канавки термического травления. Сама тормозящая сила
может быть меньше, в частности, если канавка перемещается вместе с границей. Подвижность канавки зависит от ее размера.
Малые канавки, обладая большой подвижностью, могут почти не тормозить движение границ.
Пример. При γs ≈ 2γB = 10-4 Дж/см2 в пластине толщиной 0,05 мм будет возникать тормозящая сила р9 ≈ -1 Н/см2 (-1∙104 Па).
[1] Рекристаллизация металлических материалов / Под ред. Ф. Хесснера. Пер. с англ.// М.: Металлургия. 1982. 352C.
66.
Роль кривизны границыДвижущая сила в маленьких зернах
Рассмотрим сферическое зерно радиуса r, расположенное целиком внутри монокристалла с той же удельной
свободной энергией. Оно будет стремиться сжаться, поскольку при этом уменьшается поверхностная свободная энергия.
Уравнение (1) здесь неприменимо. Движущая сила связана с изменением площади границы F и может быть записана в виде
p6=(1/F) d(FγB)/dr=2γB/r.
(19)
Этот результат справедлив вообще для любой искривленной
границы, если под r понимать средний радиус кривизны.
Рис. 4
Кривизна границы и третичная рекристаллизация
Природа использует описанный выше эффект для «распределения» локализованной движущей силы по всей
площади границы. Рассмотрим для примера движущую силу р3, связанную с различием поверхностных энергий. На рис. 4
показан бикристалл, в котором зерно I имеет более низкую поверхностную энергию, и его рост является предпочтительным.
Граница зерен начинает двигаться вперед только здесь, т.е. она начинает искривляться. Когда радиус кривизны достигает
некоторого определенного значения R, вся граница начинает двигаться как единое целое. Приравнивая р6 и р3, получаем:
R=γBω/2Δγs.
(20)
Главные радиусы кривизны цилиндрической границы на рис. 4 равны R и ∞. Средний радиус r, используемый в
уравнении (19), равен, таким образом, 2R. Следовательно, измерения могут быть использованы для оценки Δγs. Следует
отметить, что в этом случае движущая сила р6= γB/R не является добавочной движущей силой, которую следует подставлять в
уравнение (3), а только заменяет в нем движущую силу р3.
[1] Рекристаллизация металлических материалов / Под ред. Ф. Хесснера. Пер. с англ.// М.: Металлургия. 1982. 352C.
67.
Роль кривизны границы (2)Силы в клиновидном образце
Ситуация, отражающая реальный эксперимент, изображена на рис. 5. Образец представляет собой бикристалл
толщиной ω, имеющий форму клиновидной пластины. На рис. 5, а граница предполагается плоской. Тогда ее площадь
F=ωL0[1-(x/L0)2tgα].
(21)
На такую границу будут действовать
направленная вправо движущая сила
р6=(1/F)d(FγB)/dx=γB/[(L0/2tgα)-x]. (22)
В реальном эксперименте граница
подходит к поверхности под прямым углом и
должна поэтому иметь цилиндрическую
кривизну, как показано на рис 5, б, где
R=(L0/2tg α) – x
(23)
Рис. 5
и средний радиус кривизны r=2R. С учетом уравнения (19) это приводит к равенству
р6= γB /R,
(24)
идентичному уравнению (21). Кривизна границы зерен снова не требует введения добавочной движущей силы, а означает
«распределение» движущей силы равномерно по всей границе.
Пример. Если R составляет несколько сантиметров, то эта движущая сила имеет величину порядка 10-3 Н/см2 (10 Па), что меньше любой другой
движущей силы из числа обсуждаемых. Таким образом, этот эксперимент совсем не просто выполнить.
[1] Рекристаллизация металлических материалов / Под ред. Ф. Хесснера. Пер. с англ.// М.: Металлургия. 1982. 352C.
68.
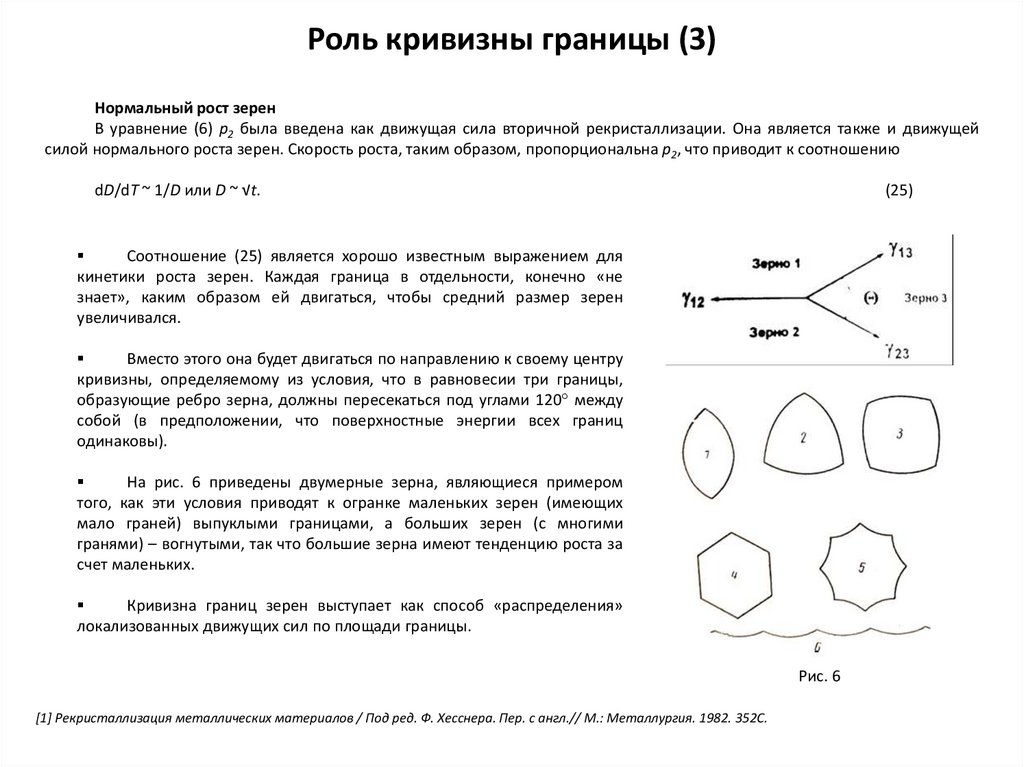
Роль кривизны границы (3)Нормальный рост зерен
В уравнение (6) р2 была введена как движущая сила вторичной рекристаллизации. Она является также и движущей
силой нормального роста зерен. Скорость роста, таким образом, пропорциональна р2, что приводит к соотношению
dD/dT ~ 1/D или D ~ √t.
(25)
Соотношение (25) является хорошо известным выражением для
кинетики роста зерен. Каждая граница в отдельности, конечно «не
знает», каким образом ей двигаться, чтобы средний размер зерен
увеличивался.
Вместо этого она будет двигаться по направлению к своему центру
кривизны, определяемому из условия, что в равновесии три границы,
образующие ребро зерна, должны пересекаться под углами 120° между
собой (в предположении, что поверхностные энергии всех границ
одинаковы).
На рис. 6 приведены двумерные зерна, являющиеся примером
того, как эти условия приводят к огранке маленьких зерен (имеющих
мало граней) выпуклыми границами, а больших зерен (с многими
гранями) – вогнутыми, так что большие зерна имеют тенденцию роста за
счет маленьких.
Кривизна границ зерен выступает как способ «распределения»
локализованных движущих сил по площади границы.
Рис. 6
[1] Рекристаллизация металлических материалов / Под ред. Ф. Хесснера. Пер. с англ.// М.: Металлургия. 1982. 352C.
69.
Равновесие между движущими и тормозящими силамиГраницы зерне совсем не будут двигаться, если сумма в правой части уравнения (3) равна нулю. Это обстоятельство
можно использовать для обсуждения различных эффектов.
Размер зерен, стабилизированных частицами второй фазы
Движущая сила нормального роста зерен р2 уменьшается по мере увеличения размера зерен. Рост зерен
прекращается, когда р2 уменьшается до значения, равного тормозящей силе р7, действующей со стороны частиц второй фазы.
Приравнивая р2 [уравнение 6] и р7 [уравнение 15], получаем:
Dlim≈2r/f.
(26)
Уравнение (26) позволяет предсказать конечный размер зерен в сплавах, имеющих промышленное значение. Оно
хорошо согласуется с экспериментом.
Влияние толщины образца
Рост зерен может прекратиться раньше, чем это обусловлено уравнением (26), если размеры образца малы хотя бы в
одном направлении (тонкие пластины или проволоки). Причиной этого является образование канавок термического
травления. Приравнивая р2 [уравнение (6)] и р9 [уравнение (18)], получаем:
Dlim≈6ω.
(27)
Если размер зерен становится сравнимым с толщиной пластины или проволоки, то уравнение (6) уже неприменимо,
поскольку при этом зерно имеет соседей только в двух (в одном) направлениях. Изменив уравнение (6), соответственно для
пластины и проволоки получим:
Dlim≈4ω и Dlim≈2ω.
Экспериментальные значения оказываются несколько меньшими.
[1] Рекристаллизация металлических материалов / Под ред. Ф. Хесснера. Пер. с англ.// М.: Металлургия. 1982. 352C.
(27, а)
70.
Равновесие между движущими и тормозящими силами (2)Пороговые напряжения при первичной рекристаллизации
Зародыши первичной рекристаллизации очень малы, поэтому согласно уравнению (19) они должны исчезать. Расти
они будут только в том случае, если движущая сила р1 [уравнение 5] будет больше, чем р6 [уравнение 19]. Это означает, что
плотность дислокаций должна превышать критическое значение:
рcrit≈2γВ/rGb2.
(28)
Зародыши имеют размеры порядка 1 мкм, т.е. рcrit≈1010 см-2. Деформации, приводящие к более низкой плотности
дислокаций, недостаточны для первичной рекристаллизации. Они приводят к другим видам рекристаллизации, таким как
миграция границ зерен под действием напряжений, когда «зародышами» служат существенно большие зерна.
Влияние магнитных полей и атмосферы отжига на текстуру рекристаллизации
Из обсуждавшихся здесь сил только две (р3 и р4) зависят от кристаллической ориентации. Они могут использоваться (и
используются) для прямого воздействия на текстуру рекристаллизации. Их влияние может стать заметным только в том
случае, если они велики или, по крайней мере, сравнимы с другими движущими силами. Сравнение сил р3 и р4 с р1, р2 и р7
показывает следующее:
а) эти силы не могут влиять на первичную рекристаллизацию;
б) атмосфера отжига может влиять на рост зерен и вторичную рекристаллизацию только если
f < r/10ω;
в) магнитное поле может повлиять на рост зерен и вторичную рекристаллизацию только если
f < Аr,
где А ≈10 см-1.
Атмосфера отжига и магнитное поле могут, таким образом, влиять на текстуру рекристаллизации лишь в таких
материалах, в которых объемная доля частиц второй фазы меньше 0,001 в предположении, что размер частиц 2r составляет
несколько микрометров.
[1] Рекристаллизация металлических материалов / Под ред. Ф. Хесснера. Пер. с англ.// М.: Металлургия. 1982. 352C.
71.
ИтогоЭлементарным процессом рекристаллизации является движение большеугловых границ зерен.
Граница движется потому, что при этом уменьшается термодинамический потенциал системы. Это
обстоятельство может быть использовано для введения «движущих сил», действующих на границу зерен, и
для оценки их величины.
Некоторые из этих движущих сил (обусловленные энергией, запасенной при холодной деформации,
зернограничной энергией в мелкозернистой матрице, энергетическими различиями кристаллитов в
магнитном поле или из-за разных поверхностных энергий, разницей энтропий между пересыщенным
твердым раствором и равновесными выделениями) приводят к росту определенных зерен.
В то же время силы, действующие со стороны растворенной примеси, выделившихся частиц второй
фазы или поверхностных канавок термического травления препятствуют движению границы и таким
образом действуют как «тормозящие силы».
Границы зерен не будут двигаться, если «движущие» и «тормозящие» силы уравновешивают одна
другую. На этой основе могут быть поняты некоторые хорошо известные явления рекристаллизации., такие
как существование пороговых напряжений первичной рекристаллизации или существование предельного
размера зерен, достигаемого при нормальном росте зерен в образце конечных размеров или в сплаве,
содержащем выделившиеся частицы.
[1] Рекристаллизация металлических материалов / Под ред. Ф. Хесснера. Пер. с англ.// М.: Металлургия. 1982. 352C.
72.
Структурные превращения в деформированных кристаллахПорядок величин различных типов движущих сил Р, обуславливающих миграцию границ зерен
Тип движущей силы
Первичная рекристаллизация
Нормальный рост
Вторичная рекристаллизация
Воздействие магнитного поля
Электромиграция
Торможение за счет включений
Р, Па
108
104
103
103
102
5۰108
Различают несколько типов движущих сил. Наиболее важные:
- запасенная энергия деформации (при первичной рекристаллизации);
- уменьшение суммарной энергии границ зерен, обуславливающее нормальный рост и
вторичную рекристаллизацию.
Если одновременно действуют несколько движущих сил, то результирующая движущая
сила составляет Р=ΣРi. При относительно малых значениях движущей силы (<104-105 Па) М и
Р являются независимыми величинами и зависимость V=MP выполняется достаточно строго.
73.
ДИНАМИЧЕСКИЕ ПРОЦЕССЫ, ПРОТЕКАЮЩИЕ В УСЛОВИЯХГОРЯЧЕЙ ПЛАСТИЧЕСКОЙ ДЕФОРМАЦИИ (ГПД)
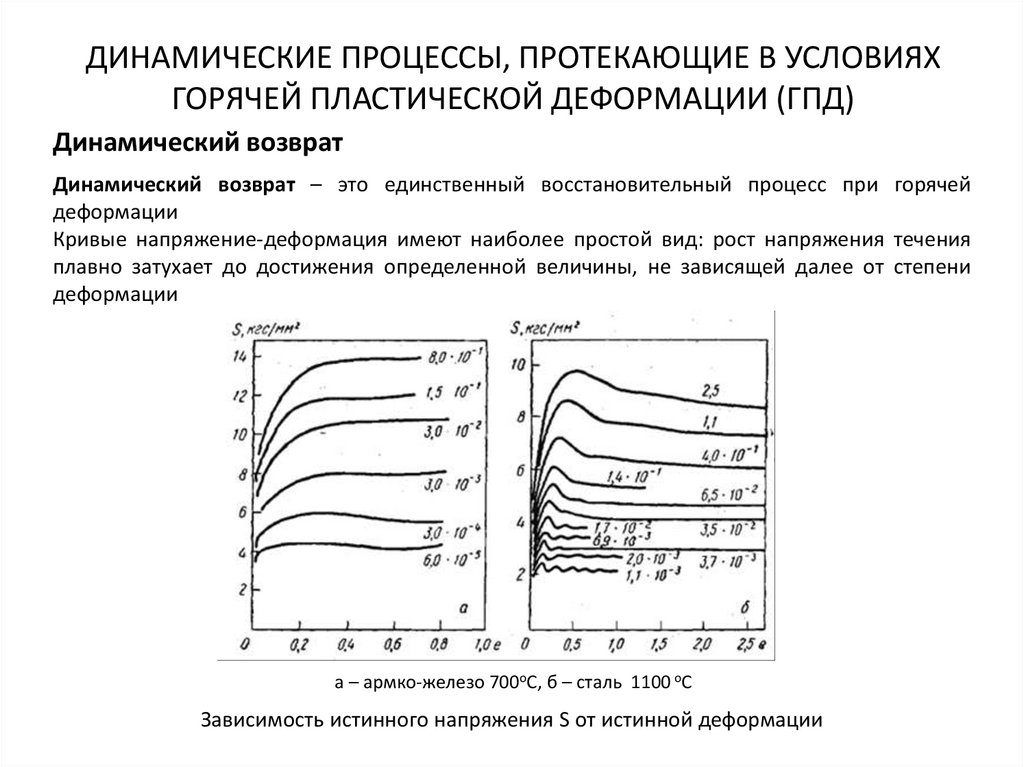
Динамический возврат
Динамический возврат – это единственный восстановительный процесс при горячей
деформации
Кривые напряжение-деформация имеют наиболее простой вид: рост напряжения течения
плавно затухает до достижения определенной величины, не зависящей далее от степени
деформации
а – армко-железо 700оС, б – сталь 1100 оС
Зависимость истинного напряжения S от истинной деформации
74.
Структура литого сплава Al-Si-Fe после деформациирастяжением при 1150°С, светлопольное изображение
Дислокации
Дефект упаковки
Чем выше температура и ниже скорость деформации, тем меньше напряжение течения на
стадии установившегося течения, меньше общая плотность дислокаций и крупнее субзерна
75.
Динамический возврат может развиваться при горячей и при холоднойдеформации.
При холодной деформации единственный механизм динамического
возврата – поперечное скольжение дислокаций, которое позволяет
дислокациям обходить барьеры и тем самым уменьшает коэффициент
деформационного упрочнения. При горячей деформации динамический
возврат, кроме поперечного скольжения, включает еще и переползание
дислокаций, в связи с чем поддерживается постоянная общая плотность
дислокаций, т. е. достигается стадия установившегося течения.
Динамический возврат металлов с более высокой энергией дефектов
упаковки идет интенсивнее и приводит к образованию более
совершенной субструктуры с более крупными субзернами, чем в металле
с низкой энергией дефектов упаковки
Металлами с активно развивающимся динамическим возвратом при
горячей деформации являются: Al, α-Fe, Mo, W, α-Zr, Be и Zn и др.
76.
Динамическая рекристаллизацияДинамическая рекристаллизация отличается от статической тем,
что появившиеся рекристаллизованные зерна с низкой плотностью
дислокаций во время своего роста постепенно наклепываются из-за
продолжающейся деформации – в них повышается плотность
дислокаций.
Характерные особенности структуры металла на стадии
динамической рекристаллизации следующие:
а) неоднородность субструктуры по объему металла и внутри
отдельных зерен;
б) неровность, зубчатость границ зерен;
в) появление колоний новых зерен преимущественно около границ
исходных кристаллов;
г) равноосность зерен.
77.
Особенности формирования структуры металлическихматериалов при ГПД
На любой стадии горячей деформации металл имеет повышенную
плотность дислокаций, которая служит термодинамическим стимулом
для восстановительных процессов после окончания деформации.
Установлены три типа самопроизвольных восстановительных
процесса, идущие по окончании горячей деформации:
1) статический возврат,
2) статическая рекристаллизация
3) метадинамическая рекристаллизация.
78.
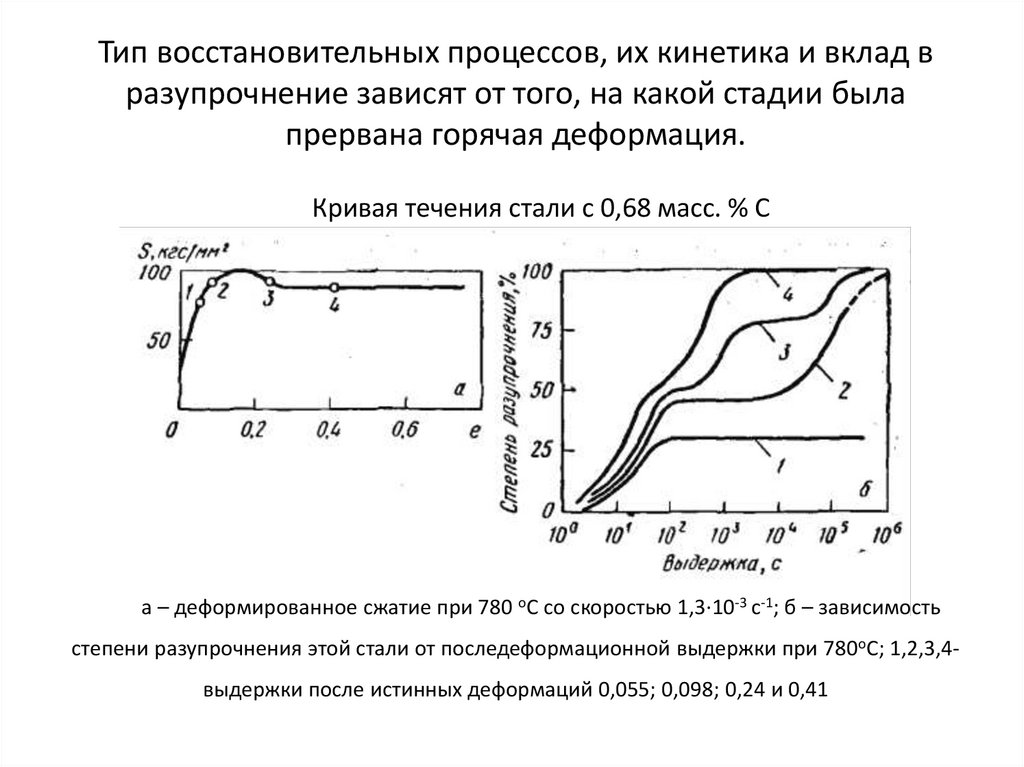
Тип восстановительных процессов, их кинетика и вклад вразупрочнение зависят от того, на какой стадии была
прервана горячая деформация.
Кривая течения стали с 0,68 масс. % С
а – деформированное сжатие при 780 оС со скоростью 1,3∙10-3 с-1; б – зависимость
степени разупрочнения этой стали от последеформационной выдержки при 780оС; 1,2,3,4выдержки после истинных деформаций 0,055; 0,098; 0,24 и 0,41
79.
Схема влияния степени горячей деформации на долюпоследеформационного упрочнения металла под действием статического
возврата, классической статической рекристаллизации и
метадинамической рекристаллизации
Если деформация е<еc, то разупрочнение является результатом только статического возврата и
никогда не бывает полным.
Если еc<е<ед , то статический возврат и позднее идущая статическая рекристаллизация
приводят к полному разупрочнению.
Если ед<е<ех, то метадинамическая рекристаллизация также дает вклад в разупрочнение.
При е > еу, разупрочнение обеспечивается статическим возвратом и метадинамической
рекристаллизацией (без участия статической рекристаллизации).
80.
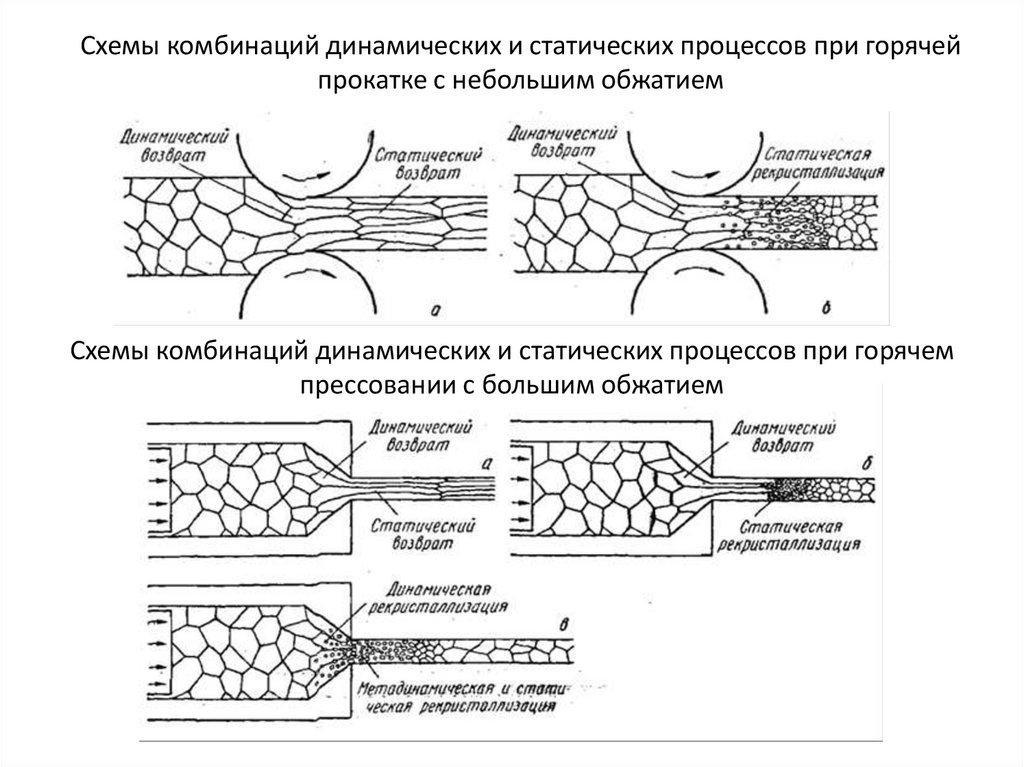
Схемы комбинаций динамических и статических процессов при горячейпрокатке с небольшим обжатием
Схемы комбинаций динамических и статических процессов при горячем
прессовании с большим обжатием




















































 Физика
Физика








