Похожие презентации:
Абстрактные кучи
1. Абстрактные кучи
2. Определение кучи
Куча – это абстрактный тип данных, оченьпохожий на бинарное дерево поиска, но
отличающийся от него двумя важными
свойствами:
• Бинарное дерево поиска считается
упорядоченным, а порядок элементов в
куче имеет совершенно другой смысл.
• Бинарное дерево поиска может иметь
разную форму, а кучи всегда являются
совершенными бинарными деревьями.
3. Определение кучи
Куча – это полное бинарное дерево, обладающееследующими свойствами:
она пуста
или
Ключ, содержащийся в ее корне, больше ключу
каждого его дочернего узла и
поддеревья корня являются кучами.
Куча называется максимальной, если корень
содержит элемент, имеющий наибольший ключ
поиска.
Куча называется минимальной, если корень
содержит элемент, имеющий наименьший ключ
поиска.
4. Операции над абстрактной кучей
MAKE NULL(Н) – делает кучу Н пустой;EMPTY(Н) – определяет, пуста ли куча;
INSERT (x,Н) – вставляет элемент х в кучу
Н;
DELETE (х,Н) – извлекает, а затем удаляет
элемент х из корня кучи Н
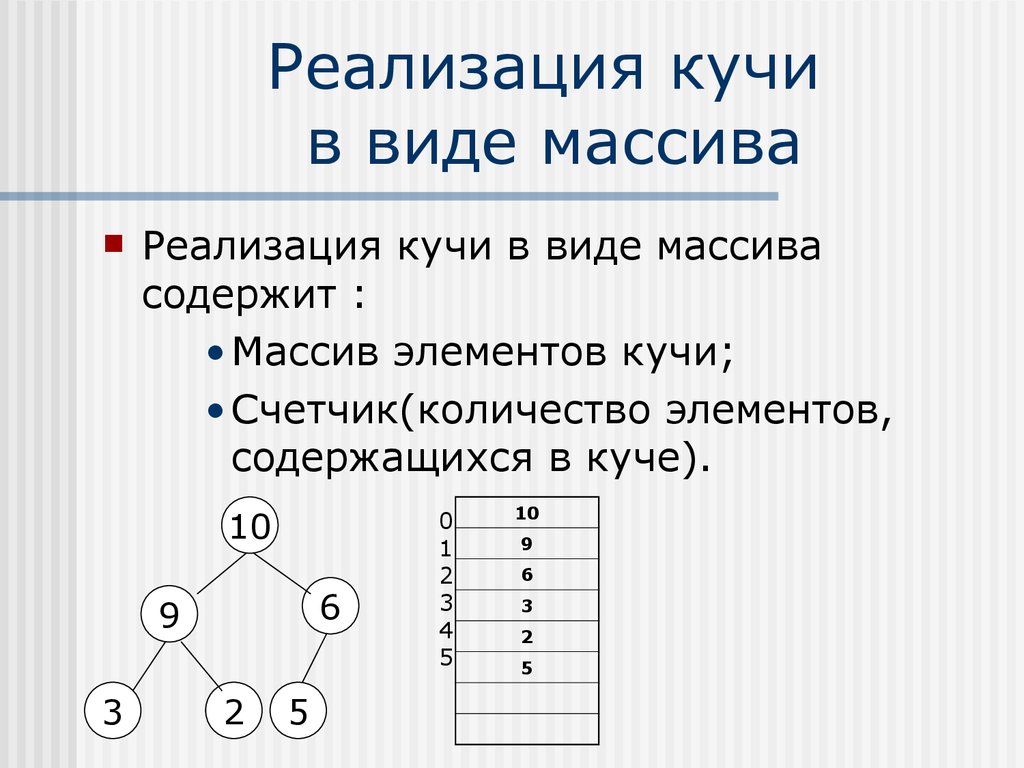
5. Реализация кучи в виде массива
Реализация кучи в виде массивасодержит :
•Массив элементов кучи;
•Счетчик(количество элементов,
содержащихся в куче).
10
6
9
3
2
5
0
1
2
3
4
5
10
9
6
3
2
5
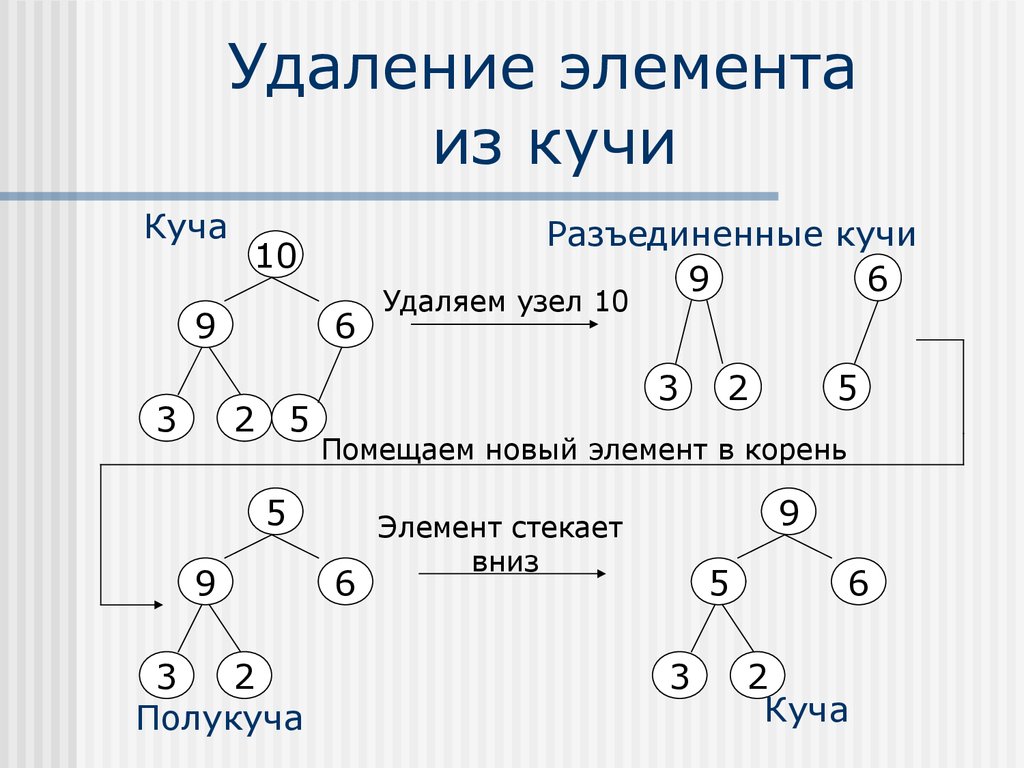
6. Удаление элемента из кучи
Куча10
9
3
Разъединенные кучи
9
6
6
2 5
3
3
2
Полукуча
2
5
Помещаем новый элемент в корень
5
9
Удаляем узел 10
6
9
Элемент стекает
вниз
5
3
6
2
Куча
7. Алгоритм удаления элемента из кучи
Находим элемент, содержащий наибольшийпоисковый ключ(корень дерева);
Удаляем этот элемент
получаем две
разъединенные кучи;
Объединяем оставшиеся узлы в новую кучу:
• Помещаем последний узел дерева в корень
Получаем полукучу (кучу, в которой элемент,
находящийся в корне кучи, находится не на своем
месте);
Находим наибольший дочерний узел(дочерний
узел с наибольшим ключом);
Меняем местами эти узлы.
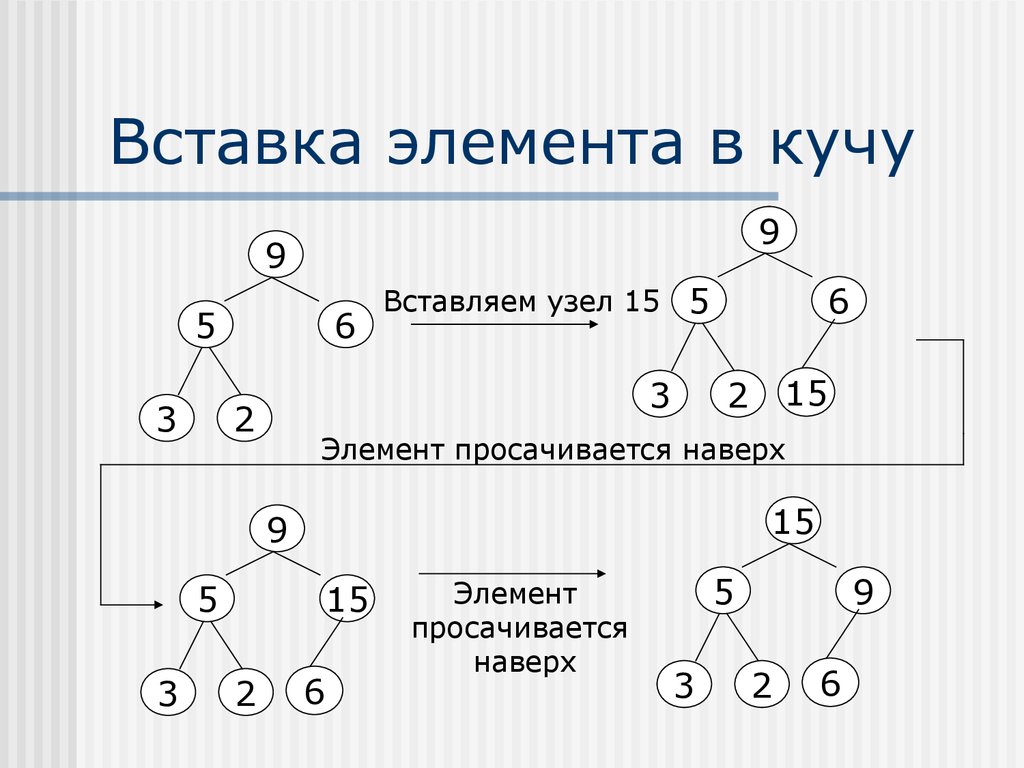
8. Вставка элемента в кучу
99
5
3
6
Вставляем узел 15
5
3
2
6
Элемент просачивается наверх
15
9
5
3
15
2
15
2
6
Элемент
просачивается
наверх
5
3
9
2
6
9. Алгоритм вставки элемента в кучу
Вставляем новый элемент воснование дерева;
Продвигаем новый элемент пока
не обнаружим подходящий узел;
Меняем местами эти элементы;






 Программирование
Программирование








