Похожие презентации:
Порядок построения развертки
1.
Лекция 9• Построение разверток пирамиды и
конуса.
• Построение разверток призмы и
цилиндра.
• Построение разверток поверхностей
Каталана
• Построение разверток поверхностей
вращения
2.
Построение развертки пирамидыЗадача: построить
развертку наклонной
усеченной пирамиды с
основанием ΔАВС и
вершиной S
Решение: Для построения
развертки пирамиды
надо найти
натуральные величины
всех ее граней.
3.
Для определения натуральныхS2
величин ребер применим метод
вращения вокруг проецирующих
j2
À02
осей. Ось вращения j проведем
B02
В.
SA в положение, параллельное
Н.
через (.) S перпендикулярно
плоскости П1. Развернем ребро
°
C02
À02
À|2
x
C2
À2
B2
плоскости П2 и найдем
натуральную величину [SA]. Т.к.
(.) А° лежит на ребре SA, она
B1
À1
°
B01
также развернется в новое
положение (на П2 фронтальная
проекция А°2 переместиться на
своей высоте на Н.В. [SA] )
À01
C1
C01
S1≡j1
° À|
A11'
4.
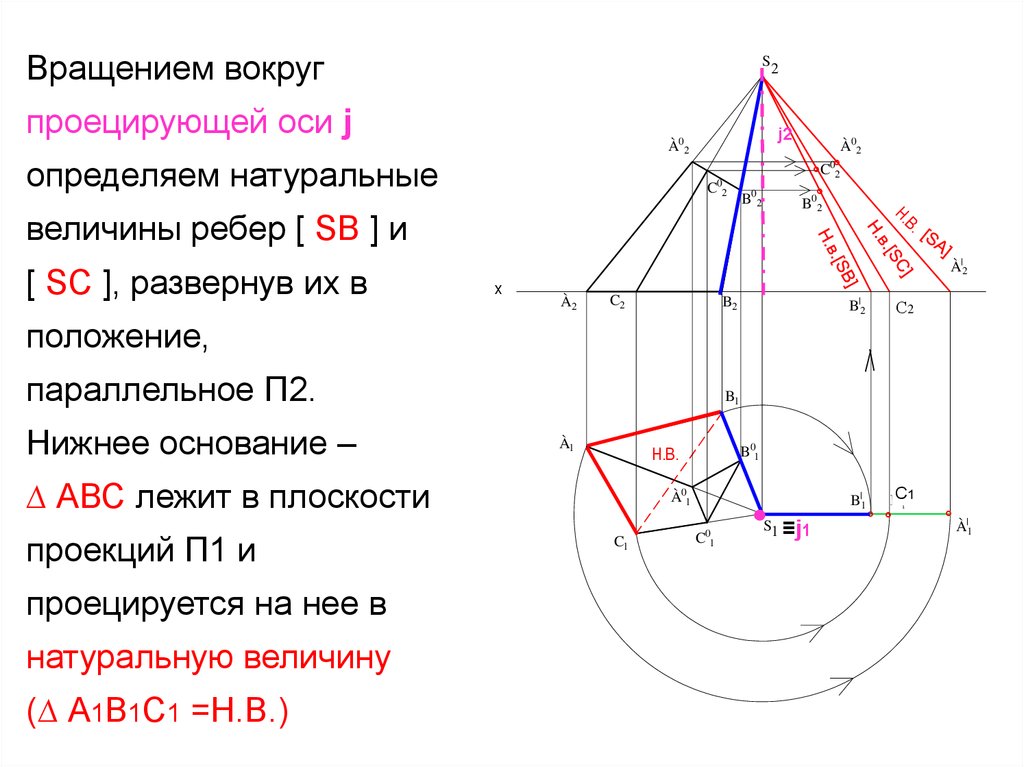
Вращением вокругS
проецирующей оси j
2
j2
À02
определяем натуральные
° C °2
B0°
0
C02
B02
2
Н.
величины ребер [ SВ ] и
В.
[ SС ], развернув их в
À02
À|2
x
À2
C2
B2
B|2
|
Ñ
С22
B|1
| 1
ÑС
1
положение,
параллельное П2.
Нижнее основание –
B1
À1
∆ АВС лежит в плоскости
проекций П1 и
проецируется на нее в
натуральную величину
(∆ А1В1С1 =Н.В.)
B01
Н.В.
À01
C1
C01
●S
1 ≡j1
° °
° À|
1
5.
SДля определения натуральной
2
величины верхнего основания
À02
ΔА°В°С° применим метод
вращения вокруг фронтально-
C02
i2
B02 C02 À02
проецирующей оси i ┴П2. Т.к.
плоскость ΔА°В°С° является
x
фронтально- проецирующей,
À2
C2
B2
развернем ее фронтальную
проекцию ΔА°2В°2С°2
параллельно плоскости П1 и
B1
À1
B01
определим натуральную
i1
величину верхнего основания –
ΔА°1В°1С°1 =Н.В.
0
À01
C1
Н.в. À 1
C01
S1 0
C1
6.
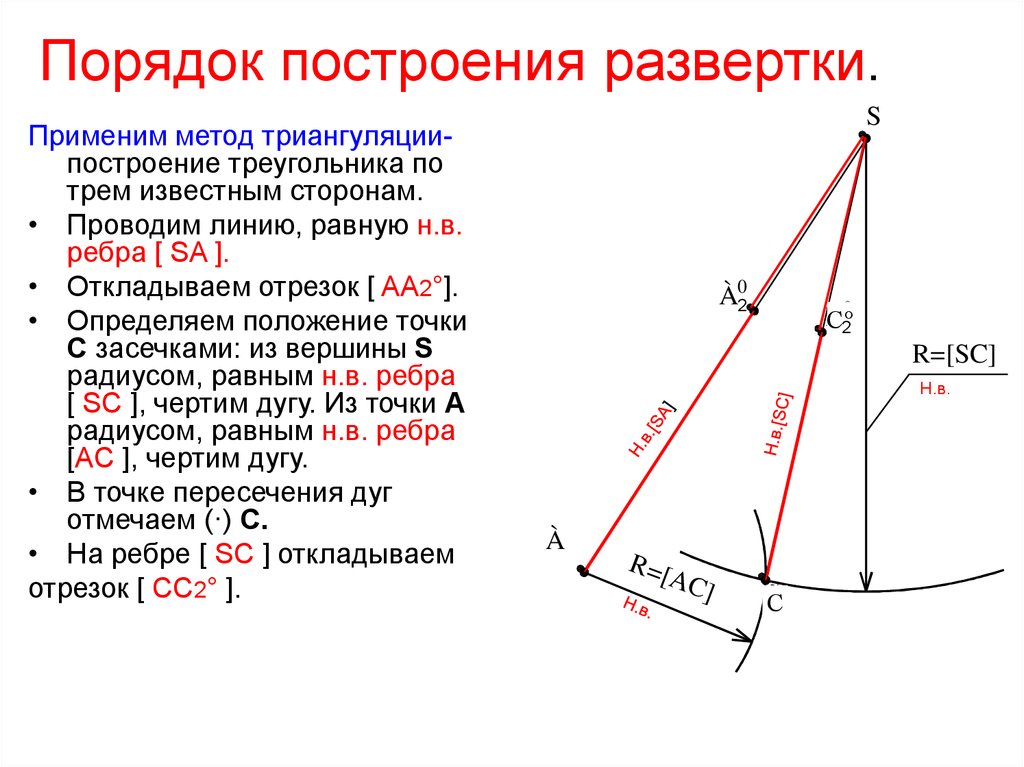
Порядок построения развертки.Применим метод триангуляциипостроение треугольника по
трем известным сторонам.
• Проводим линию, равную н.в.
ребра [ SA ].
• Откладываем отрезок [ AA2°].
• Определяем положение точки
С засечками: из вершины S
радиусом, равным н.в. ребра
[ SC ], чертим дугу. Из точки А
радиусом, равным н.в. ребра
[АC ], чертим дугу.
• В точке пересечения дуг
отмечаем (·) С.
• На ребре [ SC ] откладываем
отрезок [ СC2° ].
S
À20
0
Ñ
С°2
R=[SC]
Н.в.
À
R =[
AC]
Ñ
С
7.
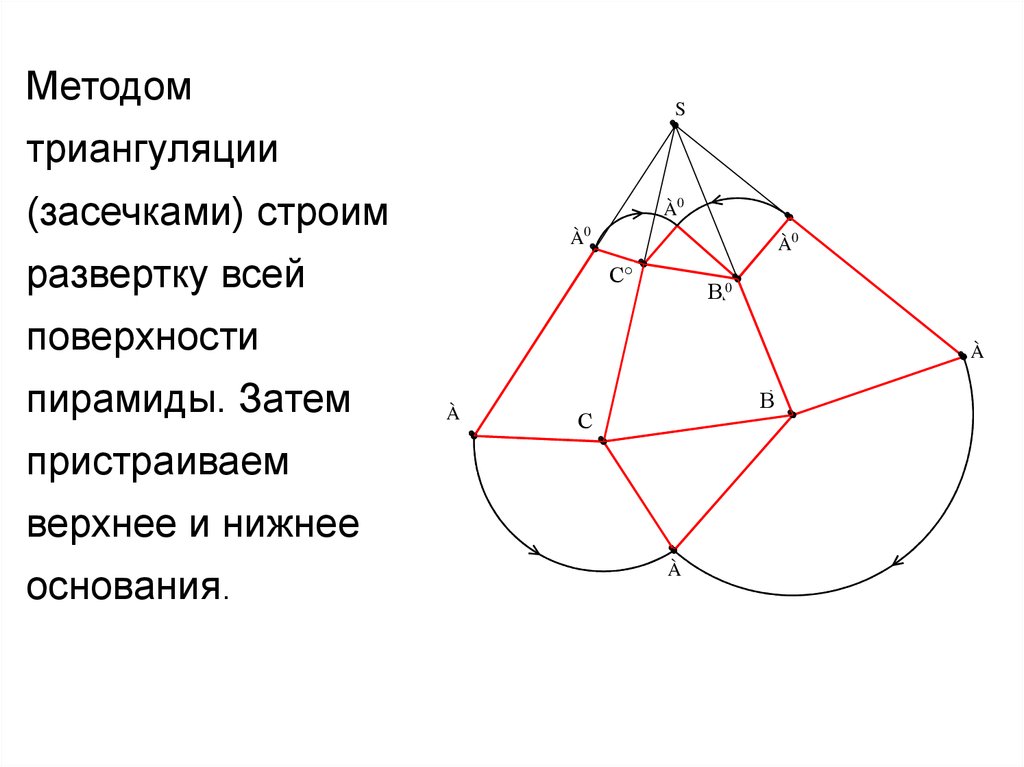
МетодомS
триангуляции
(засечками) строим
À0
À0
развертку всей
À0
С°
Ñ0
ВÂ0
поверхности
пирамиды. Затем
À
À
ВÂ
Ñ
С
пристраиваем
верхнее и нижнее
основания.
À
8.
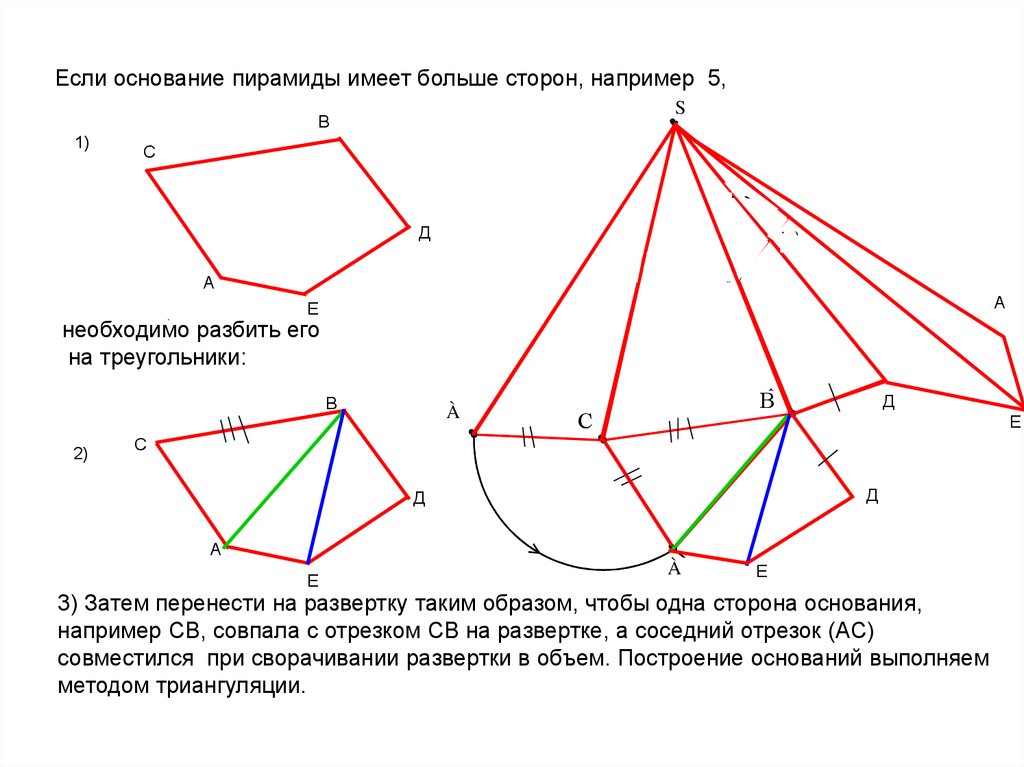
Если основание пирамиды имеет больше сторон, например 5,S
В
1)
С
À0
Д
À0
À0
Ñ0
С°
А
ВÂ0
Е
А
необходимо разбить его
на треугольники:
À
В
2)
À
ВÂ
Ñ
С
Д
Е
С
Д
Д
А
Е
À
Е
3) Затем перенести на развертку таким образом, чтобы одна сторона основания,
например СВ, совпала с отрезком СВ на развертке, а соседний отрезок (АС)
совместился при сворачивании развертки в объем. Построение оснований выполняем
методом триангуляции.
9.
Построение развертки конусаОпределитель:
вершина S и
направляющая mплоская замкнутая
кривая (окружность)
m2
m2
m1
m1
Определитель: вершина S и направляющая mпространственная незамкнутая кривая
10.
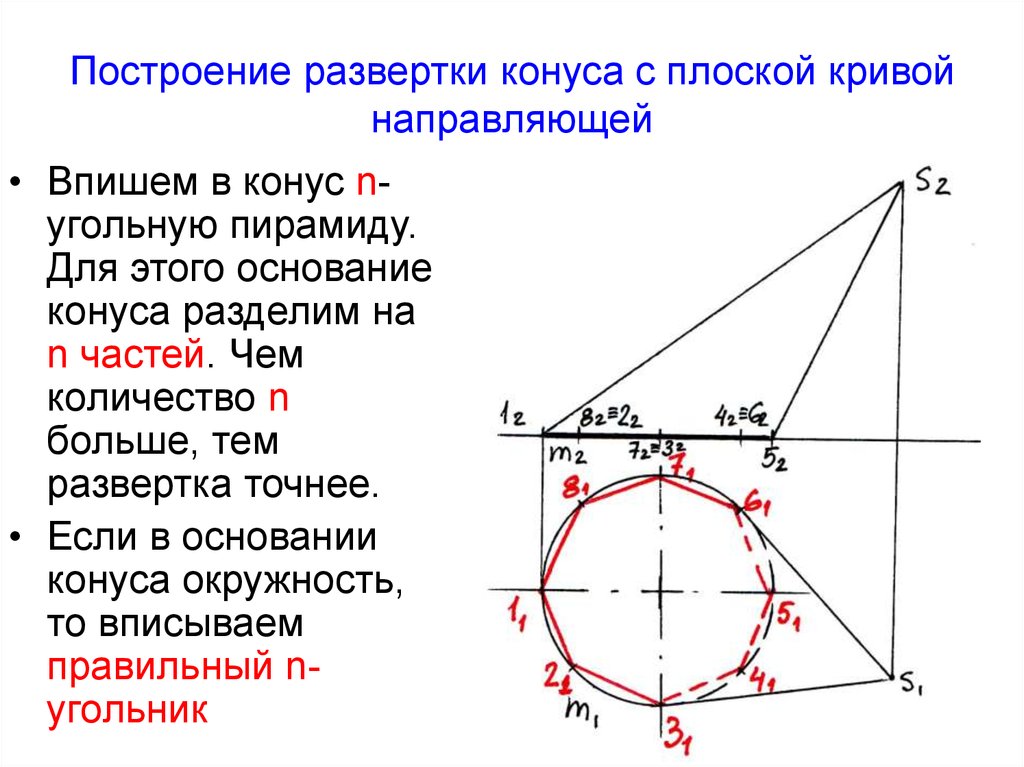
Построение развертки конуса с плоской кривойнаправляющей
• Впишем в конус nугольную пирамиду.
Для этого основание
конуса разделим на
n частей. Чем
количество n
больше, тем
развертка точнее.
• Если в основании
конуса окружность,
то вписываем
правильный nугольник
11.
Если основание лежитна П1, то оно
проецируется в
натуральную
величину. Остается
найти натуральную
величину ребер
1-S…8-S и
построить развертку
(в данном случае
восьмиугольной
пирамиды)
Н.В.
1
12.
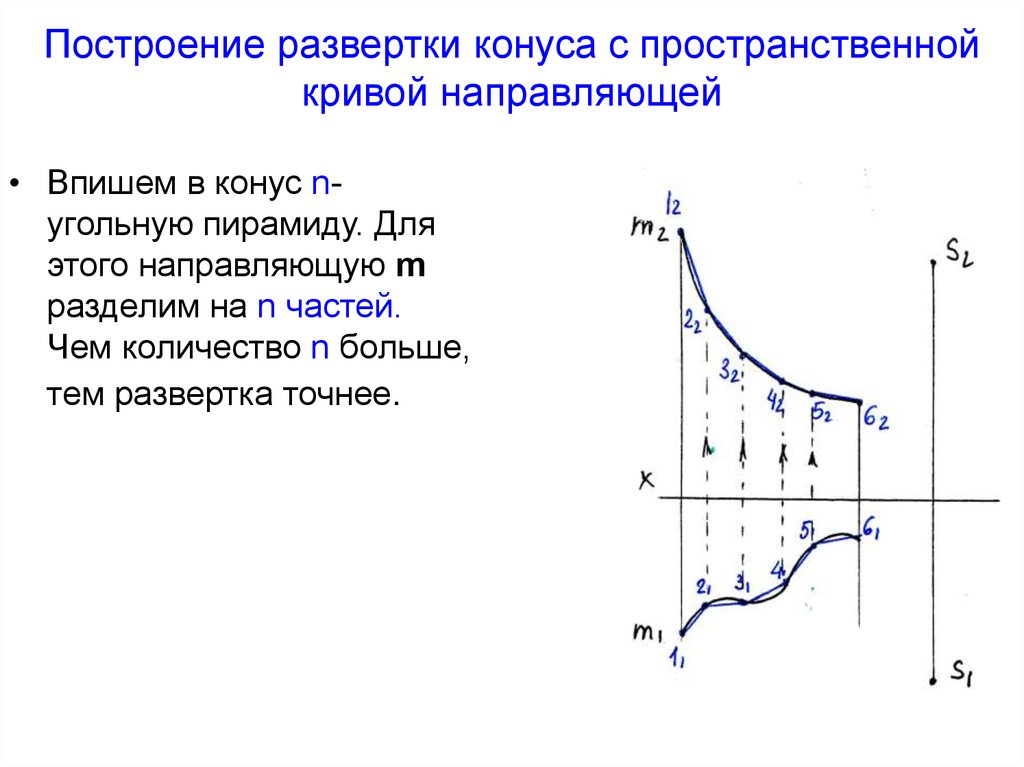
Построение развертки конуса с пространственнойкривой направляющей
• Впишем в конус nугольную пирамиду. Для
этого направляющую m
разделим на n частей.
Чем количество n больше,
тем развертка точнее.
13.
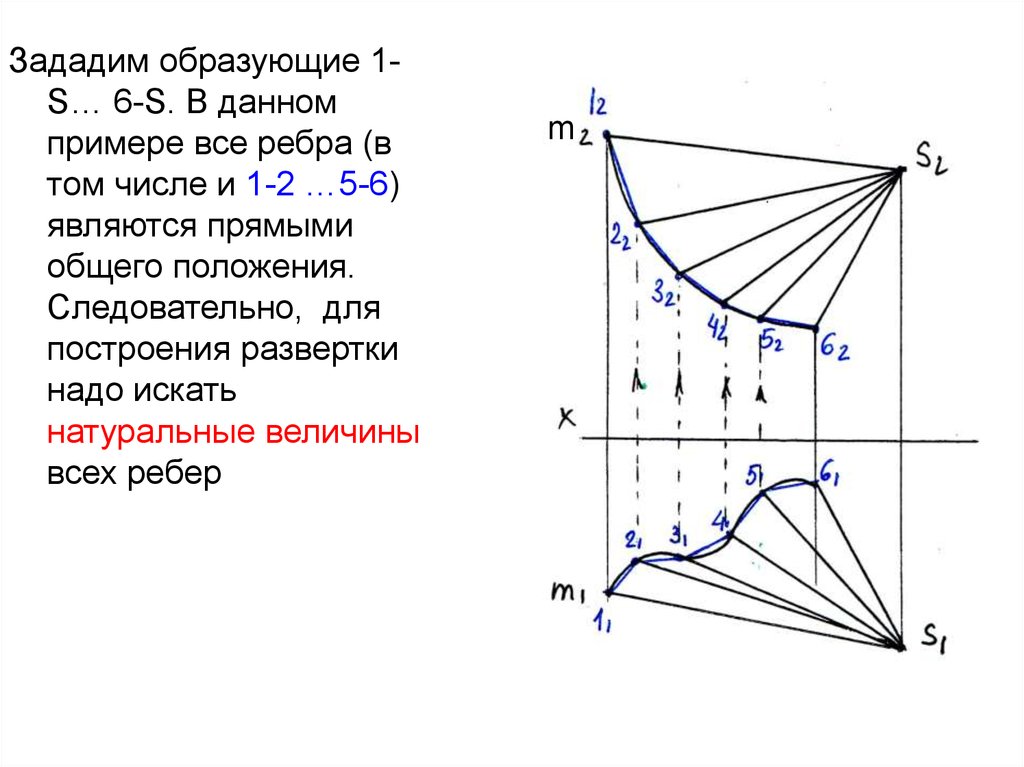
Зададим образующие 1S… 6-S. В данномпримере все ребра (в
том числе и 1-2 …5-6)
являются прямыми
общего положения.
Следовательно, для
построения развертки
надо искать
натуральные величины
всех ребер
m
14.
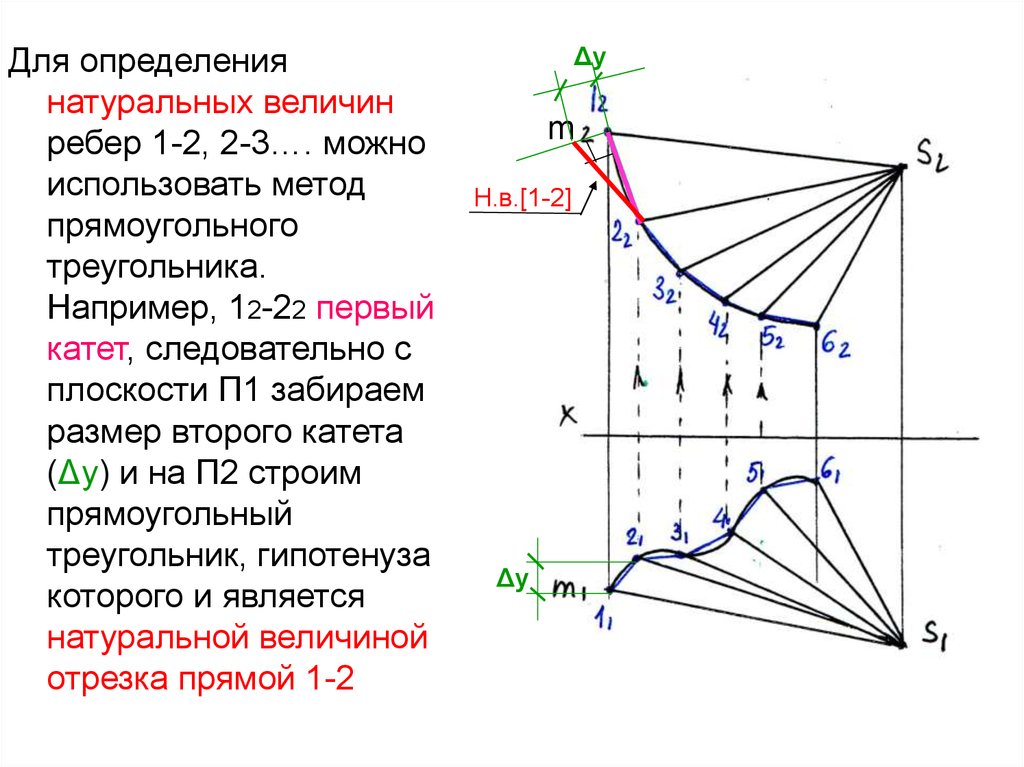
Для определениянатуральных величин
ребер 1-2, 2-3…. можно
использовать метод
прямоугольного
треугольника.
Например, 12-22 первый
катет, следовательно с
плоскости П1 забираем
размер второго катета
(Δу) и на П2 строим
прямоугольный
треугольник, гипотенуза
которого и является
натуральной величиной
отрезка прямой 1-2
Δу
m
Н.в.[1-2]
Δу
15.
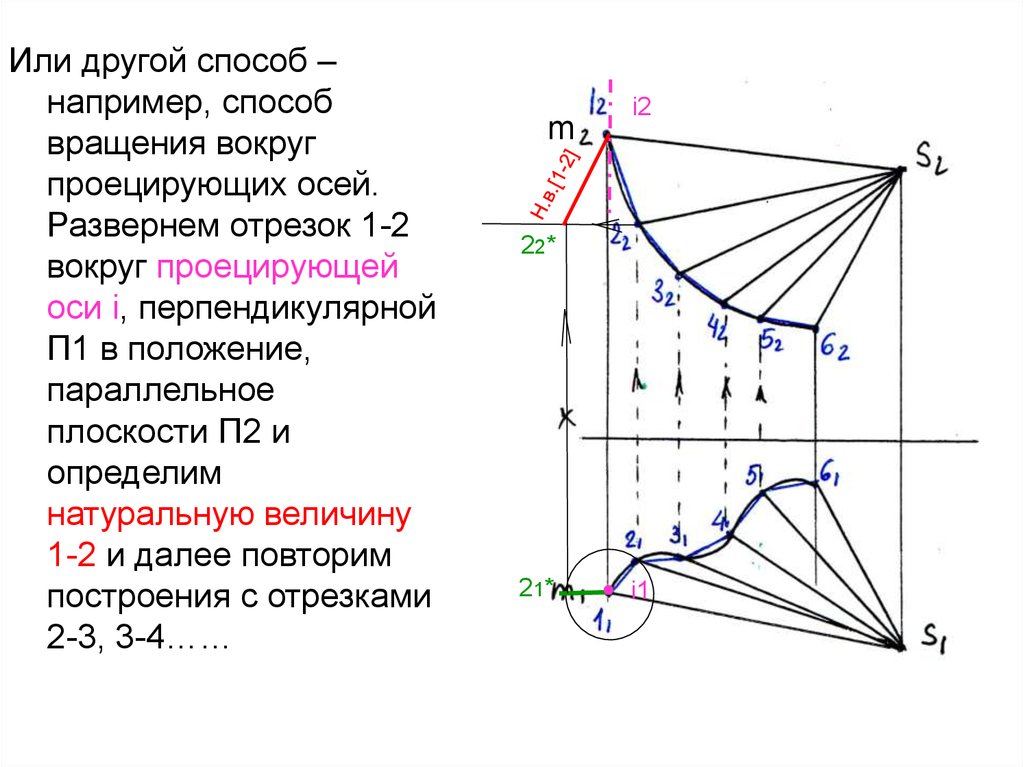
Или другой способ –например, способ
вращения вокруг
проецирующих осей.
Развернем отрезок 1-2
вокруг проецирующей
оси i, перпендикулярной
П1 в положение,
параллельное
плоскости П2 и
определим
натуральную величину
1-2 и далее повторим
построения с отрезками
2-3, 3-4……
m
i2
22*
21*
● i1
16.
i2Применим метод вращения для
определения натуральных величин
образующих 1- S, 2- S, 3- S …..
Ось вращения i проведем через
вершину S , например
перпендикулярно П1. Развернем
образующую 1- S в положение,
параллельное плоскости П2
i1 °
°
11 '
17.
i212'
°
На П2 проекция
точки 12
переместиться в
новое
положение на
высоте точки 1.
Получим
н.в. 1- S
i1 °
°
11 '
18.
i212'
°
Повторим
операцию со
всеми остальными
ребрами 2-S,
3- S… 6- S.
Затем найдем
н.в. отрезков
1-2, 2-3, 3-4…..
И далее строим
развертку
методом
триангуляции
Х
i1 °
°°
2 1 11 '
19.
Эпюр 2(курсовая работа: лист по теме
«Поверхности»)
• Эпюр 2: На листе формата А3
самостоятельно задать чертеж (фасад и
план) усечённой поверхности пирамиды
(основание-многоугольник: 4 и более
сторон) или конуса. Построить
развертку.
20.
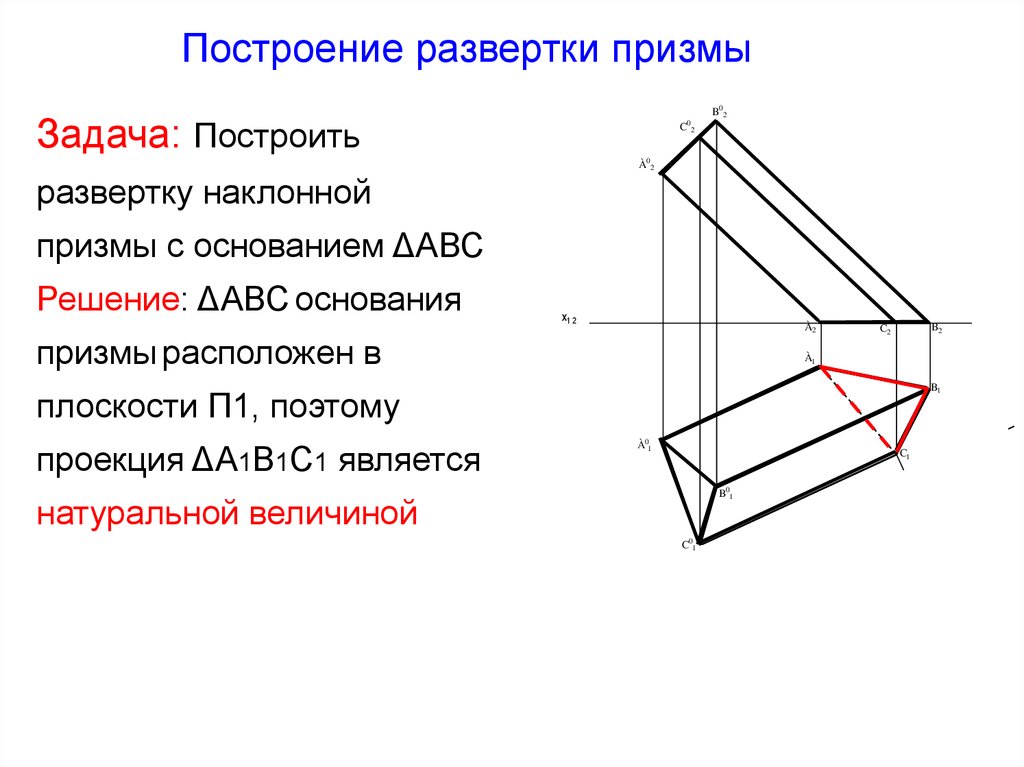
Построение развертки призмыB02
Задача: Построить
C02
À02
развертку наклонной
призмы с основанием ΔАВС
Решение: ΔАВС основания
x1 2
À2
призмы расположен в
B2
C2
À1
B1
плоскости П1, поэтому
À01
проекция ΔА1В1С1 является
C1
C4
B01
натуральной величиной
C01
Н.В
.
x1 4
C04
21.
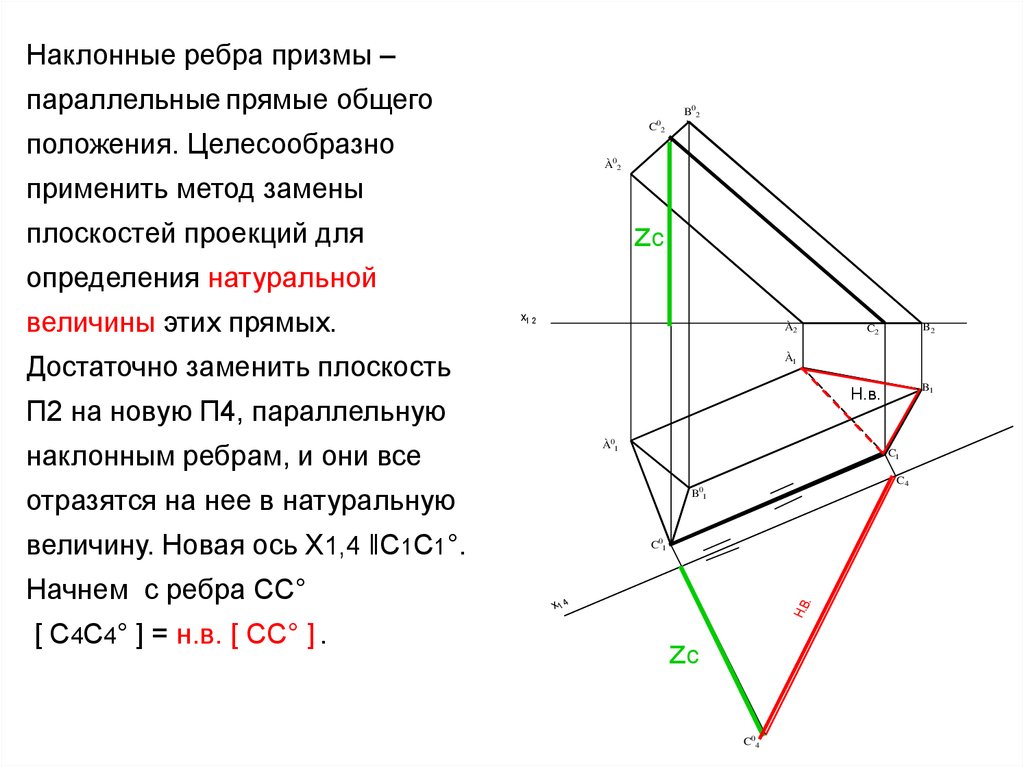
Наклонные ребра призмы –параллельные прямые общего
B02
C02
положения. Целесообразно
À02
применить метод замены
плоскостей проекций для
zc
определения натуральной
величины этих прямых.
x1 2
À2
Достаточно заменить плоскость
À01
наклонным ребрам, и они все
Н.в.
B1
C1
отразятся на нее в натуральную
C4
B01
величину. Новая ось Х1,4 ‖С1С1°.
C01
.
x1 4
Н.В
[ C4C4° ] = н.в. [ CC° ] .
B2
À1
П2 на новую П4, параллельную
Начнем с ребра СС°
C2
zc
C04
22.
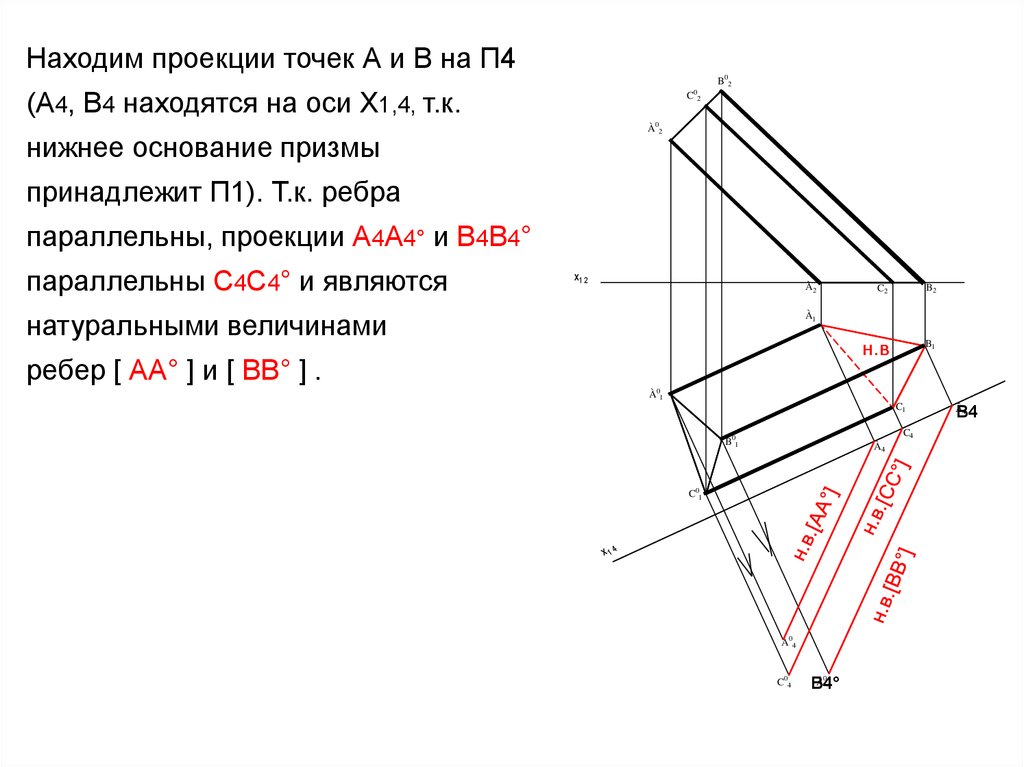
Находим проекции точек А и В на П4B02
(А4, В4 находятся на оси Х1,4, т.к.
C02
À02
нижнее основание призмы
принадлежит П1). Т.к. ребра
параллельны, проекции А4А4° и В4В4°
параллельны С4С4° и являются
x1 2
À2
натуральными величинами
C2
B2
н.в
B1
À1
ребер [ АА° ] и [ ВВ° ] .
.
À01
C1
C4
B01
À4
C01
x1 4
À04
C04
Â04
В4°
В4
Â4
23.
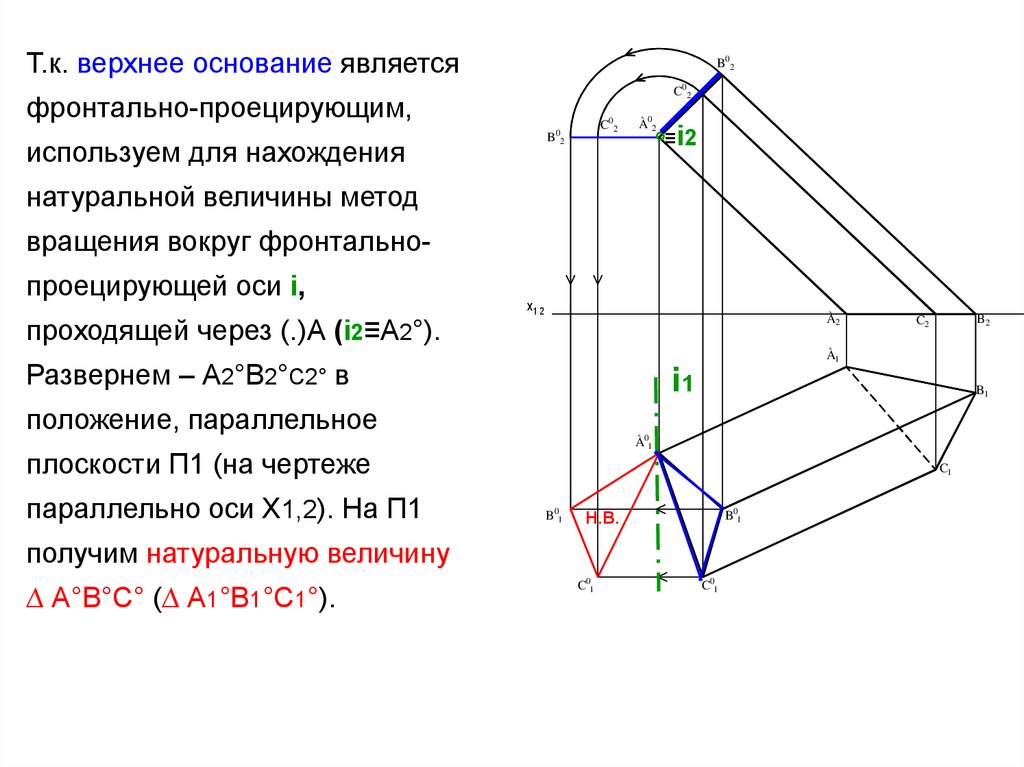
Т.к. верхнее основание являетсяB02
C02
фронтально-проецирующим,
C02
B02
используем для нахождения
À02
°≡i2
натуральной величины метод
вращения вокруг фронтальнопроецирующей оси i,
проходящей через (.)А (i2≡A2°).
x1 2
À2
À1
Развернем – А2°В2°С2° в
i1
положение, параллельное
B1
À01
плоскости П1 (на чертеже
параллельно оси Х1,2). На П1
C1
B01
B01
Н.В.
получим натуральную величину
∆ А°В°С° (∆ А1°В1°С1°).
B2
C2
C01
C01
24.
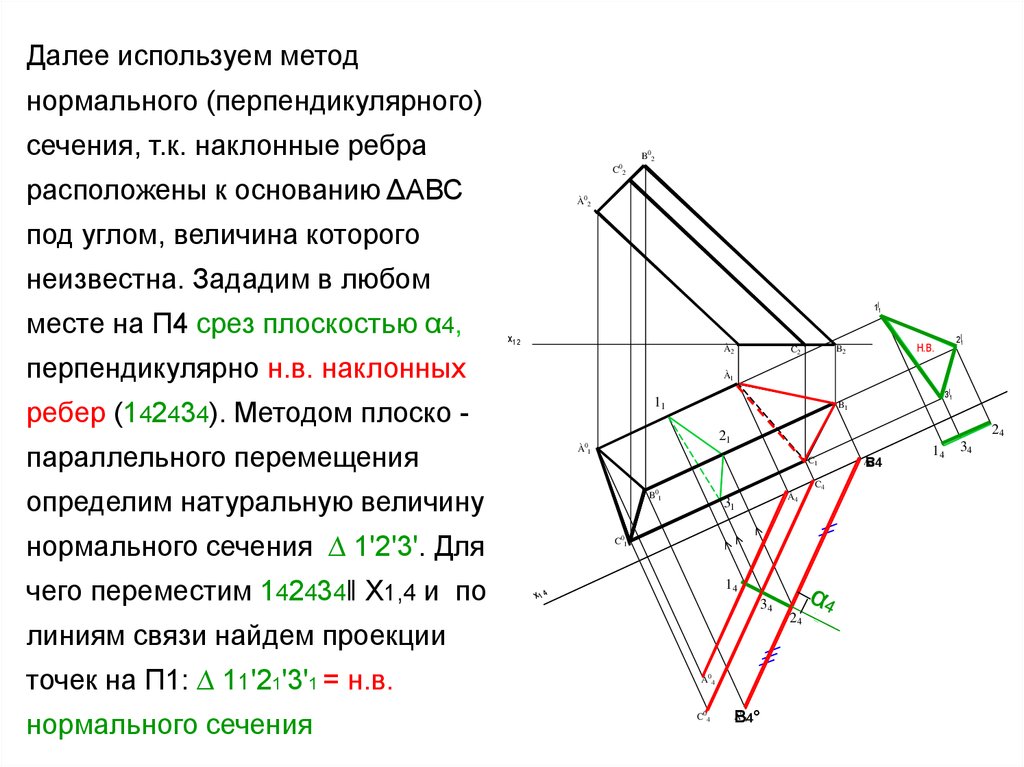
Далее используем методнормального (перпендикулярного)
сечения, т.к. наклонные ребра
B02
C02
расположены к основанию ΔАВС
À02
под углом, величина которого
неизвестна. Зададим в любом
месте на П4 срез плоскостью α4,
1|1
x1 2
À2
перпендикулярно н.в. наклонных
À1
ребер (142434). Методом плоско -
11
параллельного перемещения
24
21
C1
C4
B01
нормального сечения ∆ 1'2'3'. Для
À4
31
C01
14
x1 4
34
линиям связи найдем проекции
точек на П1: ∆ 11'21'3'1 = н.в.
нормального сечения
3|1
B1
À01
определим натуральную величину
чего переместим 142434‖ Х1,4 и по
2|1
Н.В.
B2
C2
À04
C04
 4°
В
0
4
24
4
в
Â4 4
14
34
25.
Порядок построения развертки.• Развернем в линию
натуральную величину
нормального сечения
На горизонтальной линии
откладываем отрезки
[ 1‘-2' ], [ 2‘-3' ], [ 3‘-1' ].
À0
C0
0
À
B0
1|
2|
À0
1|
3|
À
À
C
B
À
26.
Через отмеченные точки проводимлинии, перпендикулярные отрезкам и
À0
откладываем на них натуральные
величины наклонных ребер призмы.
Вниз от нормального сечения
C0
0
À
B0
1|
2|
À0
откладываем отрезки [ 14А4 ], [ 24В4 ],
[ 34С4 ].
1|
3|
Вверх от нормального сечения
откладываем отрезки
[ 14А4° ], [ 24В4° ], [ 34С4° ], измеряя
À
À
данные отрезки на П4
C
B
À
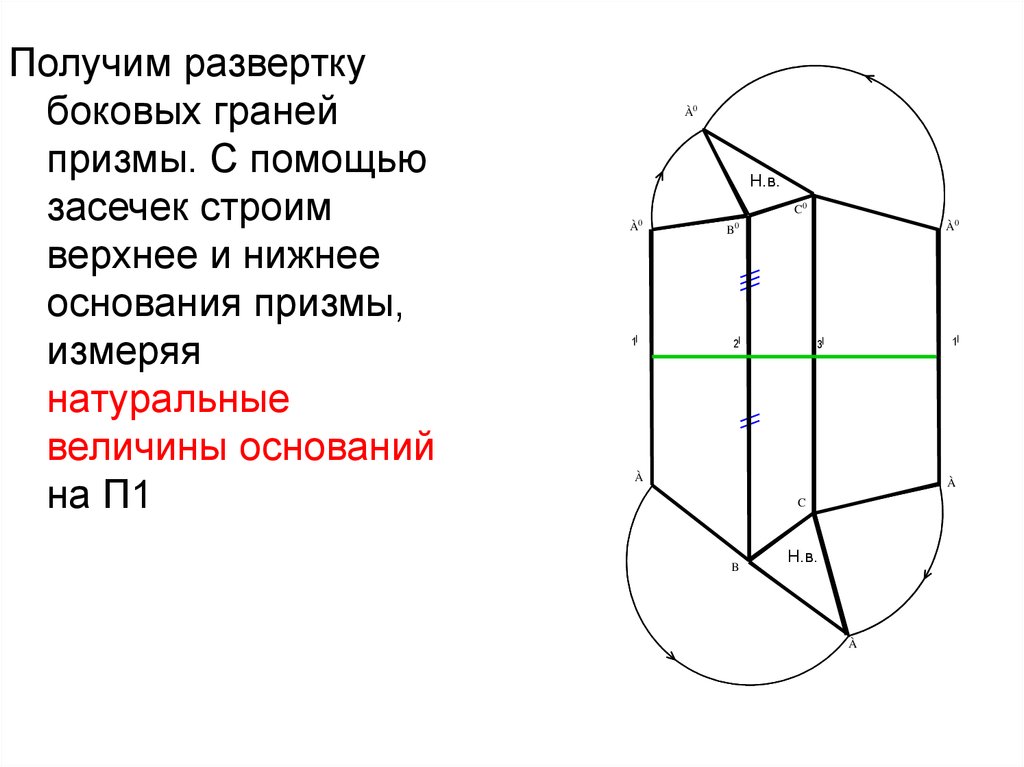
27.
Получим разверткубоковых граней
призмы. С помощью
засечек строим
верхнее и нижнее
основания призмы,
измеряя
натуральные
величины оснований
на П1
À0
Н.в.
C0
0
À
B0
1|
2|
À0
1|
3|
À
À
C
B
Н.в.
À
28.
Построение развертки цилиндраОпределитель:
направление S и
направляющая mплоская замкнутая
кривая (окружность)
S2
S1
Определитель: направление S и направляющая
m- пространственная не замкнутая кривая
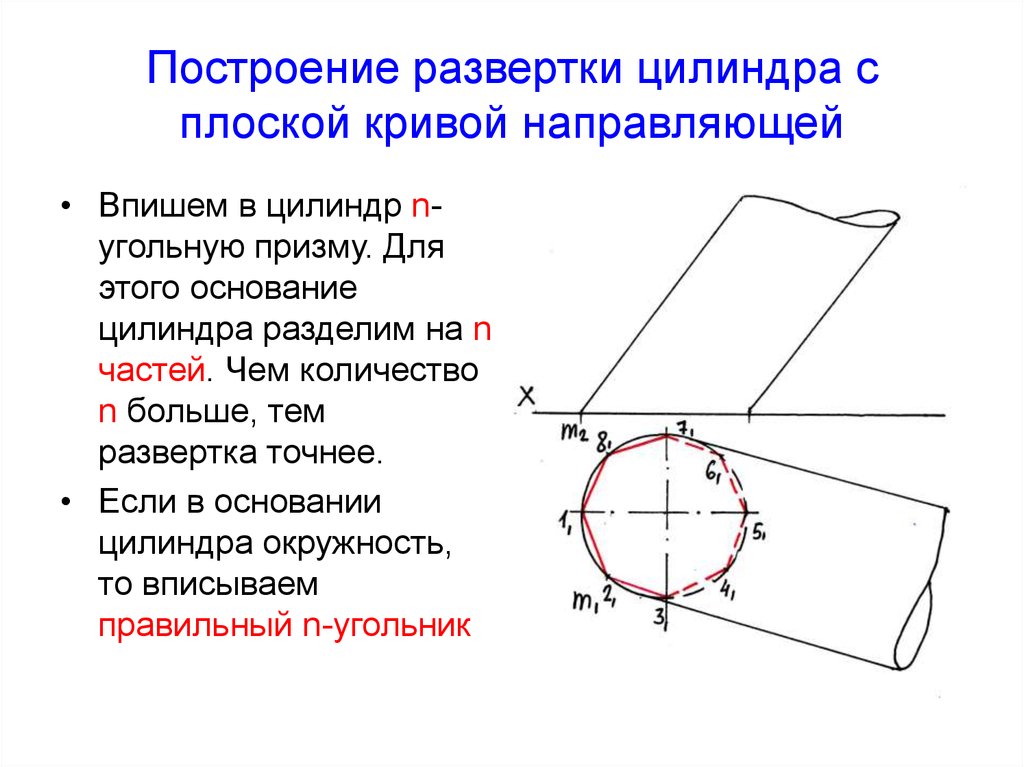
29.
Построение развертки цилиндра сплоской кривой направляющей
• Впишем в цилиндр nугольную призму. Для
этого основание
цилиндра разделим на n
частей. Чем количество
n больше, тем
развертка точнее.
• Если в основании
цилиндра окружность,
то вписываем
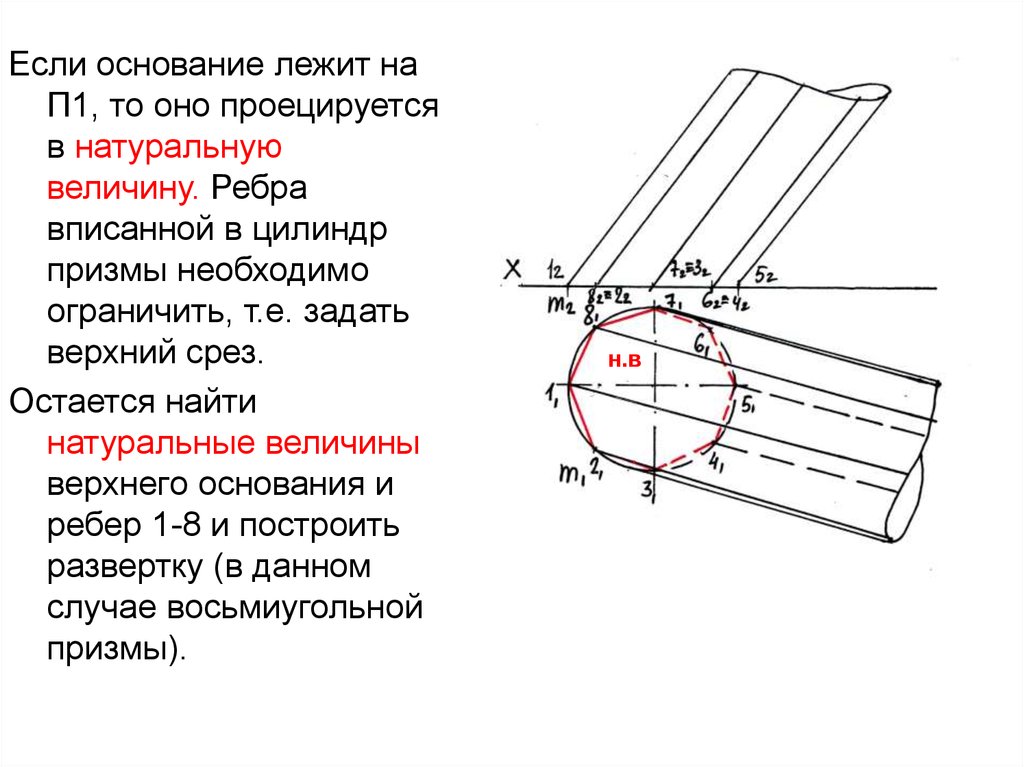
правильный n-угольник
30.
Если основание лежит наП1, то оно проецируется
в натуральную
величину. Ребра
вписанной в цилиндр
призмы необходимо
ограничить, т.е. задать
верхний срез.
Остается найти
натуральные величины
верхнего основания и
ребер 1-8 и построить
развертку (в данном
случае восьмиугольной
призмы).
н.в
.
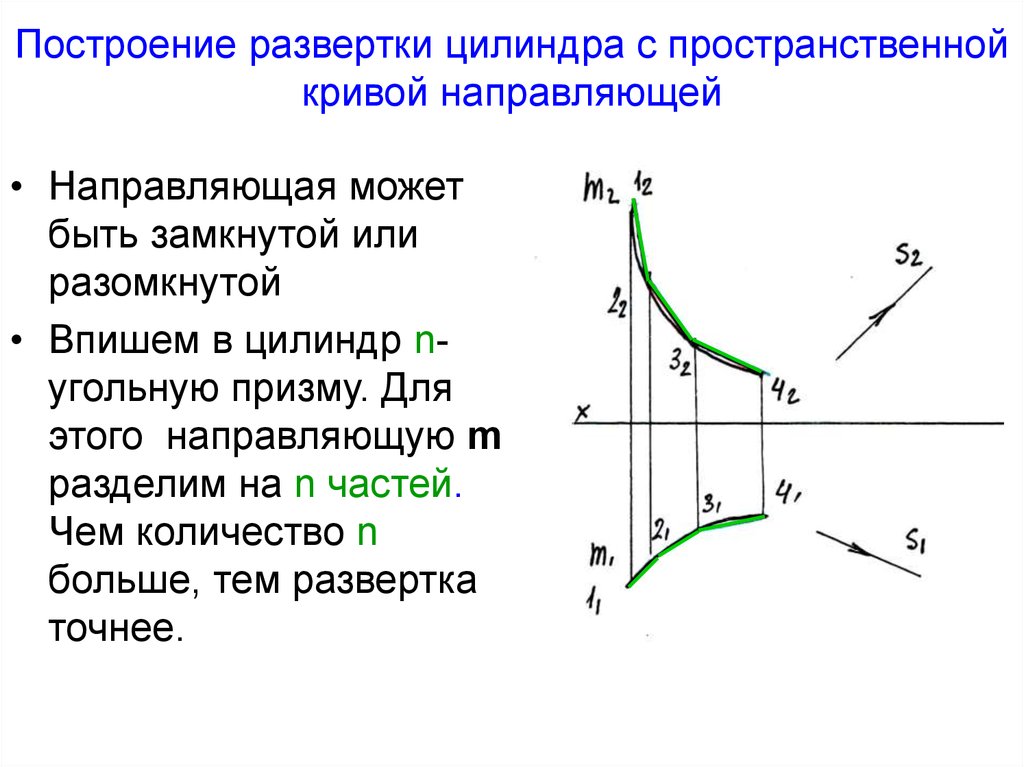
31.
Построение развертки цилиндра с пространственнойкривой направляющей
• Направляющая может
быть замкнутой или
разомкнутой
• Впишем в цилиндр nугольную призму. Для
этого направляющую m
разделим на n частей.
Чем количество n
больше, тем развертка
точнее.
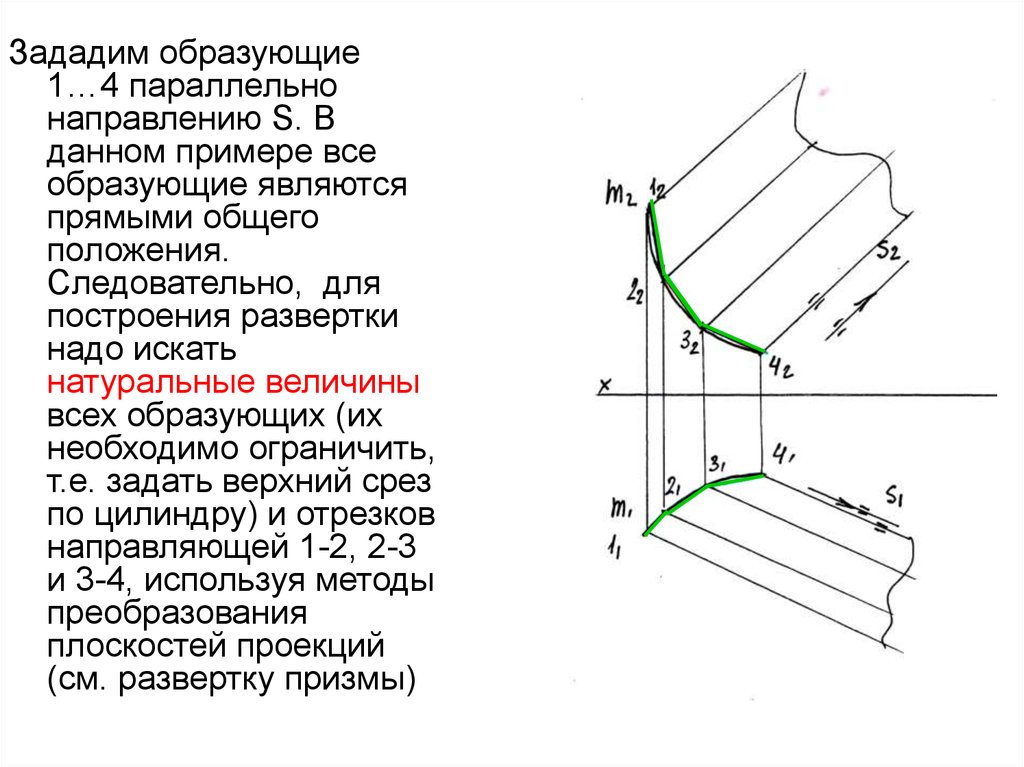
32.
Зададим образующие1…4 параллельно
направлению S. В
данном примере все
образующие являются
прямыми общего
положения.
Следовательно, для
построения развертки
надо искать
натуральные величины
всех образующих (их
необходимо ограничить,
т.е. задать верхний срез
по цилиндру) и отрезков
направляющей 1-2, 2-3
и 3-4, используя методы
преобразования
плоскостей проекций
(см. развертку призмы)
33.
Эпюр 3(курсовая работа: лист по теме
«Поверхности»)
• Эпюр 3: На листе формата А3
самостоятельно задать чертеж (фасад и
план) усечённой поверхности призмы
(основание: многоугольник 4 и более
сторон) или цилиндра. Построить
развертку.
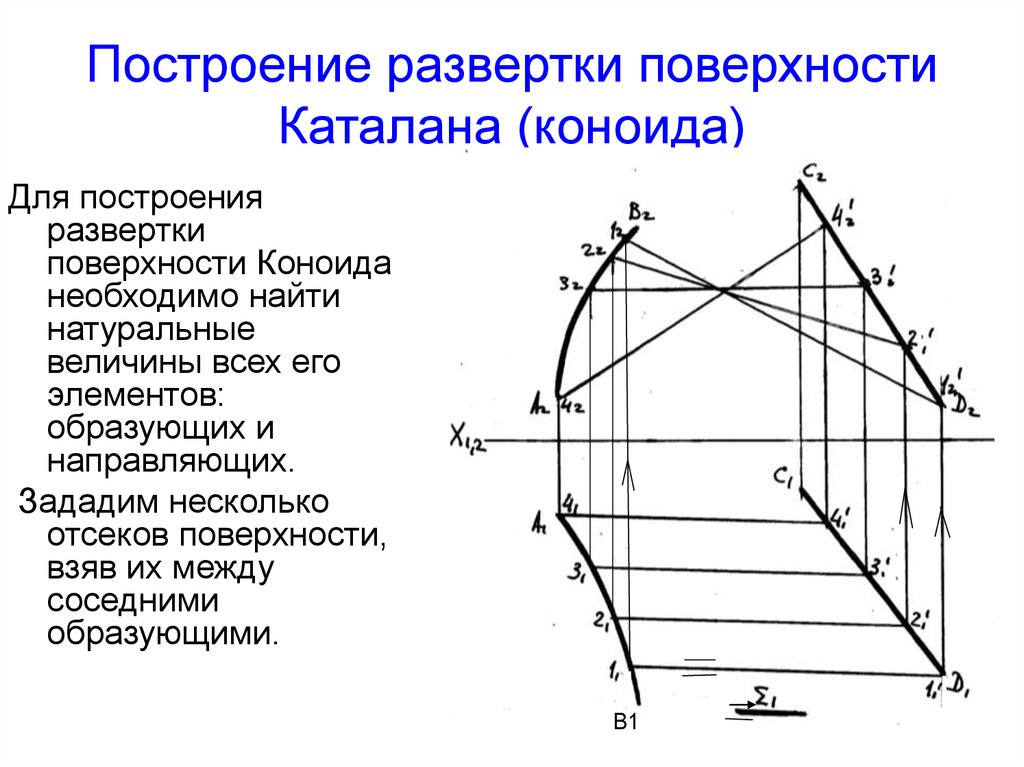
34.
Построение развертки поверхностиКаталана (коноида)
Для построения
развертки
поверхности Коноида
необходимо найти
натуральные
величины всех его
элементов:
образующих и
направляющих.
Зададим несколько
отсеков поверхности,
взяв их между
соседними
образующими.
В1
35.
Т.к. образующие 1-1', 2-2 ‘, 3-3 ‘ и4-4 ‘ расположены
параллельно плоскости Σ1, их
натуральную величину
следует искать методом
замены плоскостей проекций.
Заменим плоскость П2 на
новую П4 ‖ Σ1 (на чертеже
новая ось Х1,4 ‖ Σ1).
Забираем высоты точек с П2
и откладываем их по линиям
связи с соответствующими
горизонтальными проекциями
этих точек на П4. Проекция
образующей 14-14' на П4 =
натуральной величине.
Z1
Z1'
Z1'
Z1
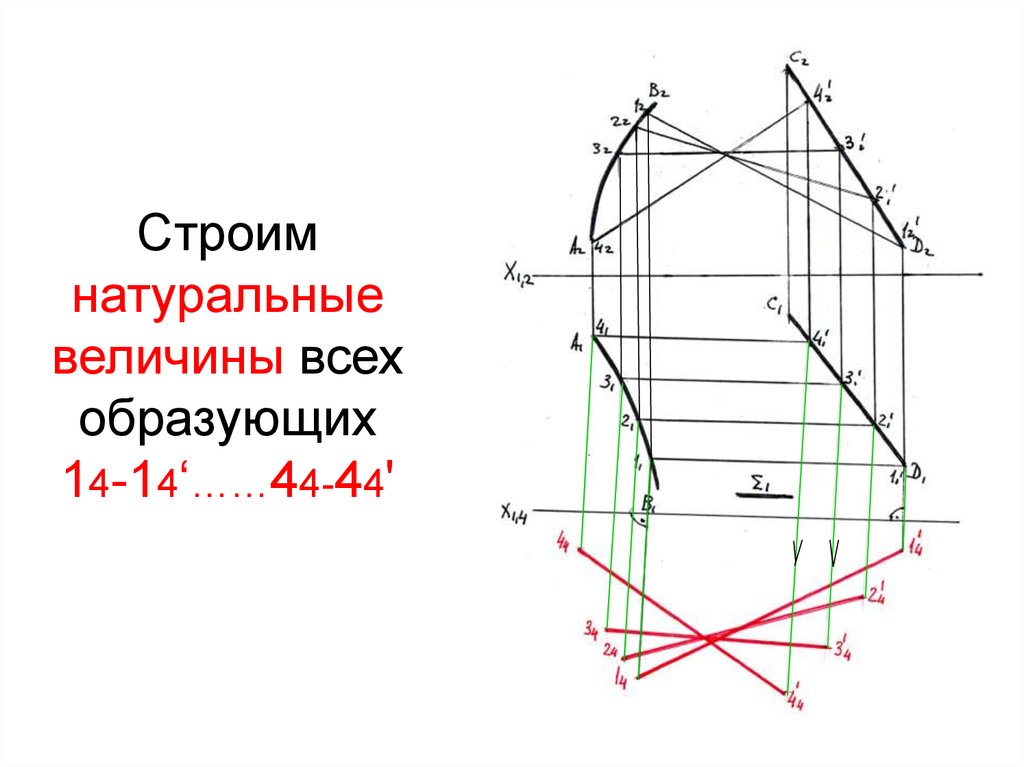
36.
Строимнатуральные
величины всех
образующих
14-14‘……44-44'
37.
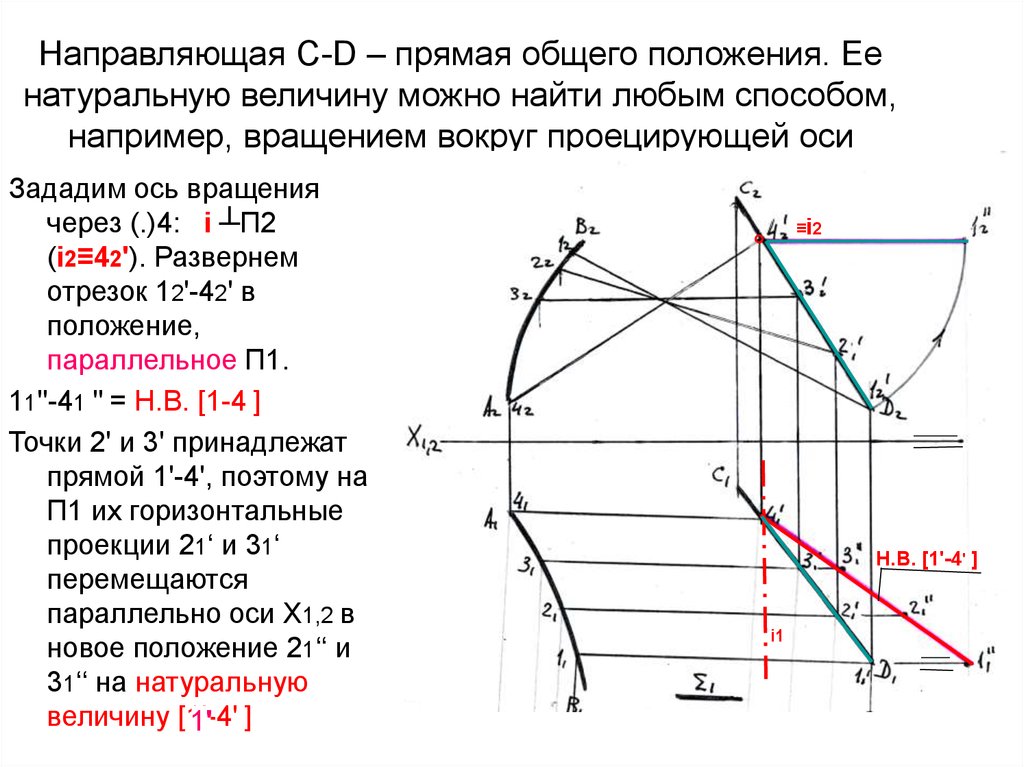
Направляющая С-D – прямая общего положения. Еенатуральную величину можно найти любым способом,
например, вращением вокруг проецирующей оси
Зададим ось вращения
через (.)4: i ┴П2
(i2≡42'). Развернем
отрезок 12'-42' в
положение,
параллельное П1.
11''-41 '' = Н.В. [1-4 ]
Точки 2' и 3' принадлежат
прямой 1'-4', поэтому на
П1 их горизонтальные
проекции 21‘ и 31‘
перемещаются
параллельно оси Х1,2 в
новое положение 21‘‘ и
31‘‘ на натуральную
величину [1'-4'
1' ]
≡i2
°
Н.В. [1'-4' ]
i1
38.
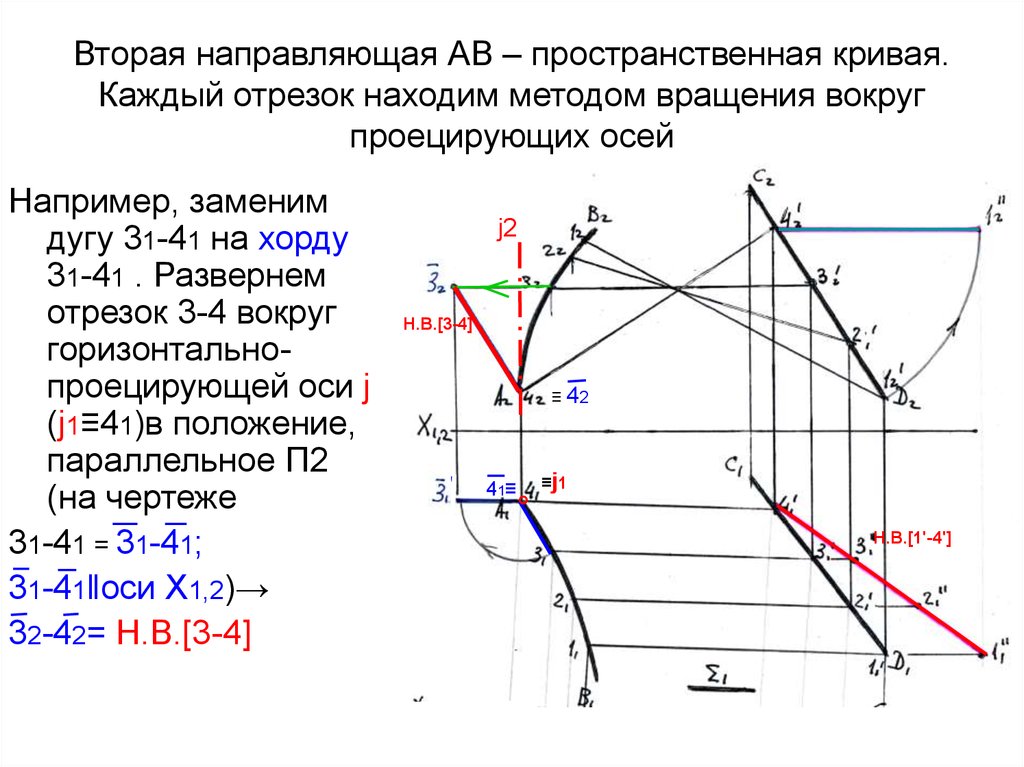
Вторая направляющая АВ – пространственная кривая.Каждый отрезок находим методом вращения вокруг
проецирующих осей
Например, заменим
дугу 31-41 на хорду
31-41 . Развернем
отрезок 3-4 вокруг
горизонтальнопроецирующей оси j
(j1≡41)в положение,
параллельное П2
(на чертеже
31-41 = 31-41;
31-41‖оси Х1,2)→
32-42= Н.В.[3-4]
j2
'
Н.В.[3-4]
≡ 42
'
41≡
°
≡j1
Н.В.[1'-4']
39.
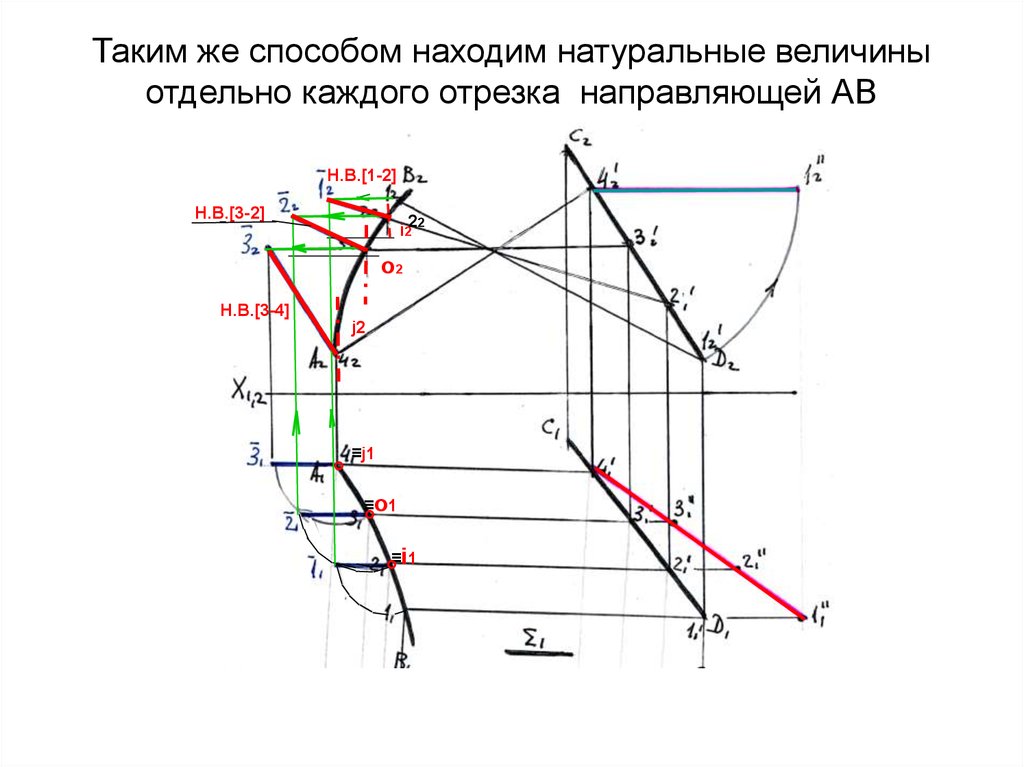
Таким же способом находим натуральные величиныотдельно каждого отрезка направляющей АВ
Н.В.[1-2]
Н.В.[3-2]
i222
о2
Н.В.[3-4]
j2
°
≡j1
≡о1
°
≡i1
°
40.
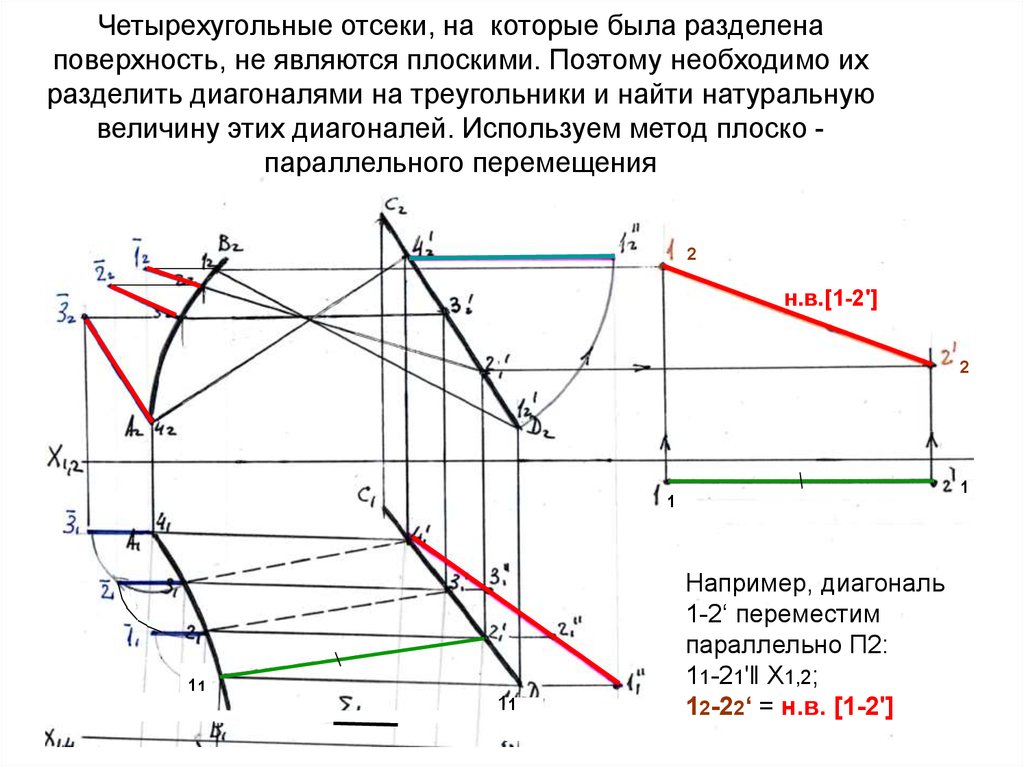
Четырехугольные отсеки, на которые была разделенаповерхность, не являются плоскими. Поэтому необходимо их
разделить диагоналями на треугольники и найти натуральную
величину этих диагоналей. Используем метод плоско параллельного перемещения
2
н.в.[1-2']
2
1
1
11
11
Например, диагональ
1-2‘ переместим
параллельно П2:
11-21'‖ Х1,2;
12-22‘ = н.в. [1-2']
41.
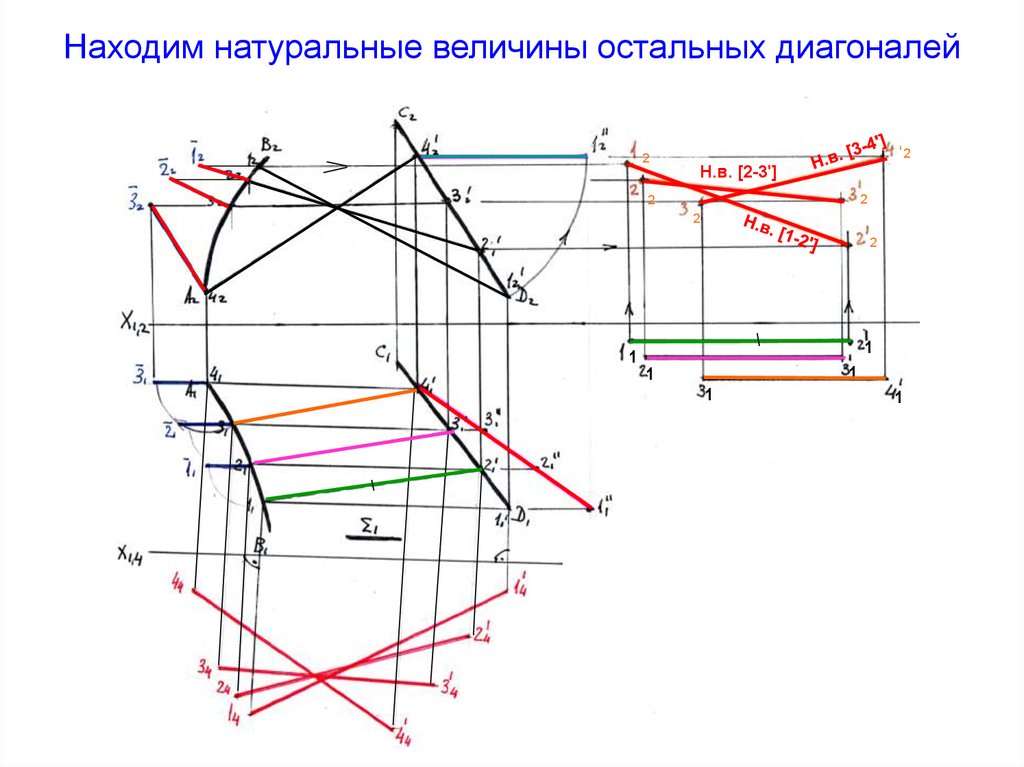
Находим натуральные величины остальных диагоналей2
‘2
Н.в. [2-3']
2
2
2
2
1
1
1
1
1
1
42.
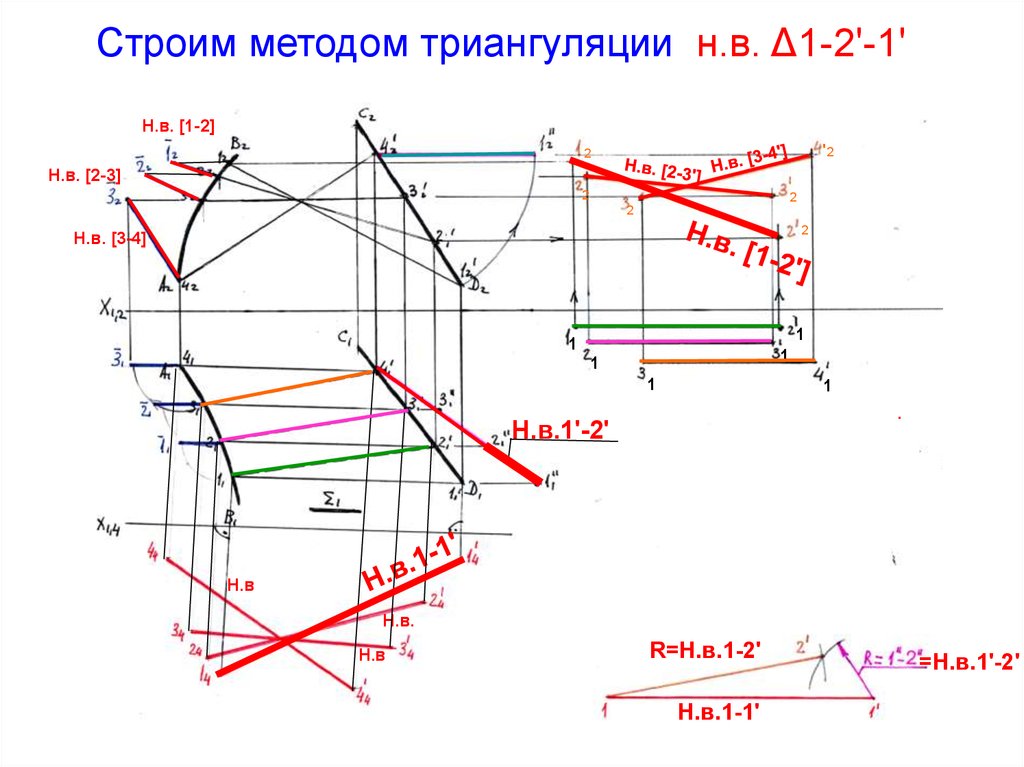
Строим методом триангуляции н.в. Δ1-2'-1'Н.в. [1-2]
'2
2
Н.в. [2-3]
2
2
2
2
Н.в. [3-4]
1
1
1
1
1
1
.
Н.в.1'-2'
Н.в
Н.в.
Н.в
R=Н.в.1-2'
Н.в.1-1'
=Н.в.1'-2'
43.
Завершаем построение развертки, последовательно выстраиваяследующие треугольники. Используем только натуральные величины
найденных отрезков
Н.в.1-2
'
R=Н.в.2-2'
R=Н.в.1-2
44.
Эпюр 4(курсовая работа: лист по теме
«Поверхности»)
• Эпюр 4: На листе формата А3
самостоятельно задать чертеж (фасад и
план) поверхности Каталана
(цилиндроид, или коноид, или косая
плоскость). Построить развертку (не
менее 5-и отсеков)
45.
Построение разверткиповерхности сферы
Сферическая поверхность не
развертываемая. Сферу нельзя
развернуть в плоскость без
разрывов и складок. Поэтому
можно построить лишь условную
развертку.
Один из способов построения
развертки заключается в
аппроксимации (замене)
сферических элементов на
цилиндрические.
Поверхность сферы разделим
меридианами на части (доли). Чем
количество долей больше, тем
развертка точнее.
Участки поверхности, заключенные между
смежными меридианами, заменяются
цилиндрической поверхностью,
касательной к сфере по главному
меридиану.
46.
Построим развертку одной доли. Наметим ось симметрии элемента, накоторой отложим длину главного меридиана = н.в. Для этого разделим
главный меридиан на 6 равных частей.
Н.в.главного меридиана
.
2
1
2
3
3
4
4
5
1
5
2
3
4
5
Н.в.главного меридиана
1
6 штук
В точках 1,2….5. на развертке отложим размер ширины доли , который берем с П1
47.
Эпюр 5(курсовая работа: лист по теме
«Поверхности»)
• Эпюр 5: На листе формата А3
самостоятельно задать чертеж (фасад и
план) поверхности вращения (сферу не
задавать!). Построить развертку: план
разбить минимум на 8 частей.
Криволинейные участки образующей
(главный меридиан) на фасаде заменить
ломаной линией, максимально приближенной
к кривой образующей.




















 Инженерная графика
Инженерная графика








