Алгоритмы комбинаторной оптимизации. Тема 10 - 11

1. Тема 10. Алгоритмы комбинаторной оптимизации

Программирование и основы алгоритмизации
Тема 10. Алгоритмы
комбинаторной оптимизации
Шевченко А. В.
Тема 11. Алгоритмы комбинаторной оптимизации
1

2. Задачи комбинаторной оптимизации

Программирование и основы алгоритмизации
Задачи комбинаторной оптимизации
Пример 1. Производство краски
В производстве краски при смене цвета требуется
очистка оборудования. Время очистки зависит от
того, с какой краски на какую осуществляется
переход. Требуется выбрать последовательность
смены цвета, которая давала бы минимальную
длительность производственного цикла.
Шевченко А. В.
Тема 11. Алгоритмы комбинаторной оптимизации
2

3. Задачи комбинаторной оптимизации

Программирование и основы алгоритмизации
Задачи комбинаторной оптимизации
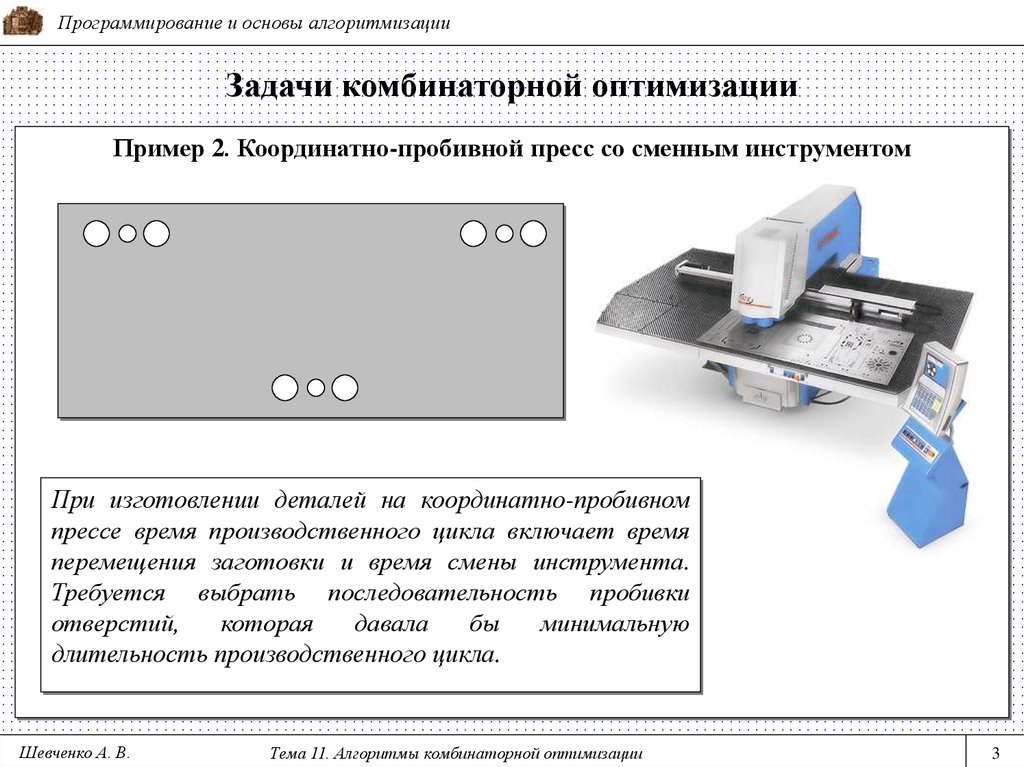
Пример 2. Координатно-пробивной пресс со сменным инструментом
При изготовлении деталей на координатно-пробивном
прессе время производственного цикла включает время
перемещения заготовки и время смены инструмента.
Требуется выбрать последовательность пробивки
отверстий,
которая
давала
бы
минимальную
длительность производственного цикла.
Шевченко А. В.
Тема 11. Алгоритмы комбинаторной оптимизации
3

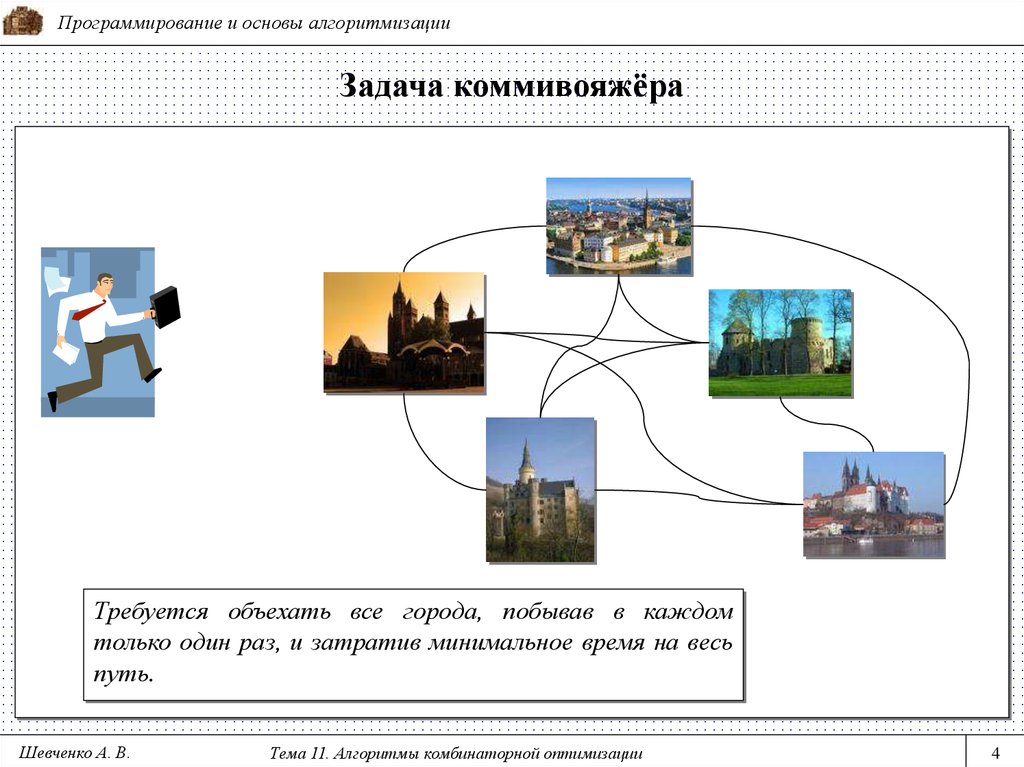
4. Задача коммивояжёра

Программирование и основы алгоритмизации
Задача коммивояжёра
Требуется объехать все города, побывав в каждом
только один раз, и затратив минимальное время на весь
путь.
Шевченко А. В.
Тема 11. Алгоритмы комбинаторной оптимизации
4

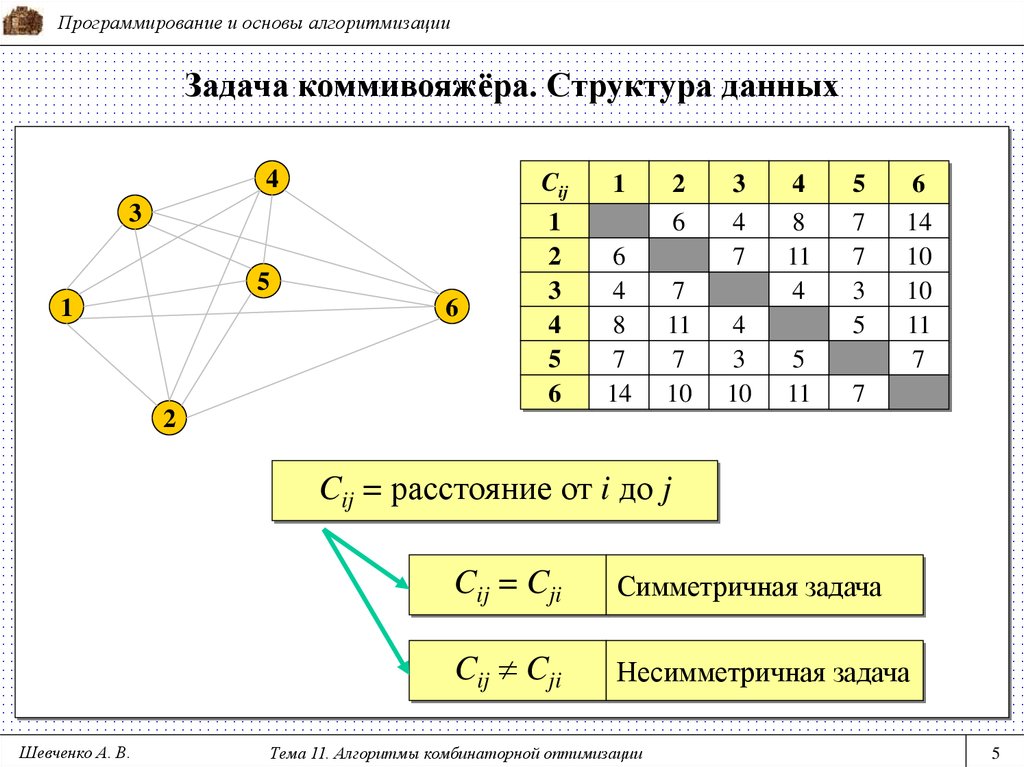
5. Задача коммивояжёра. Структура данных

Программирование и основы алгоритмизации
Задача коммивояжёра. Структура данных
4
Cij
3
5
1
6
1
2
3
4
5
6
1
6
4
8
7
14
2
3
4
5
6
6
4
7
8
11
4
7
7
3
5
14
10
10
11
7
7
11
7
10
4
3
10
5
11
7
2
Cij = расстояние от i до j
Шевченко А. В.
Cij = Cji
Симметричная задача
Cij Cji
Несимметричная задача
Тема 11. Алгоритмы комбинаторной оптимизации
5

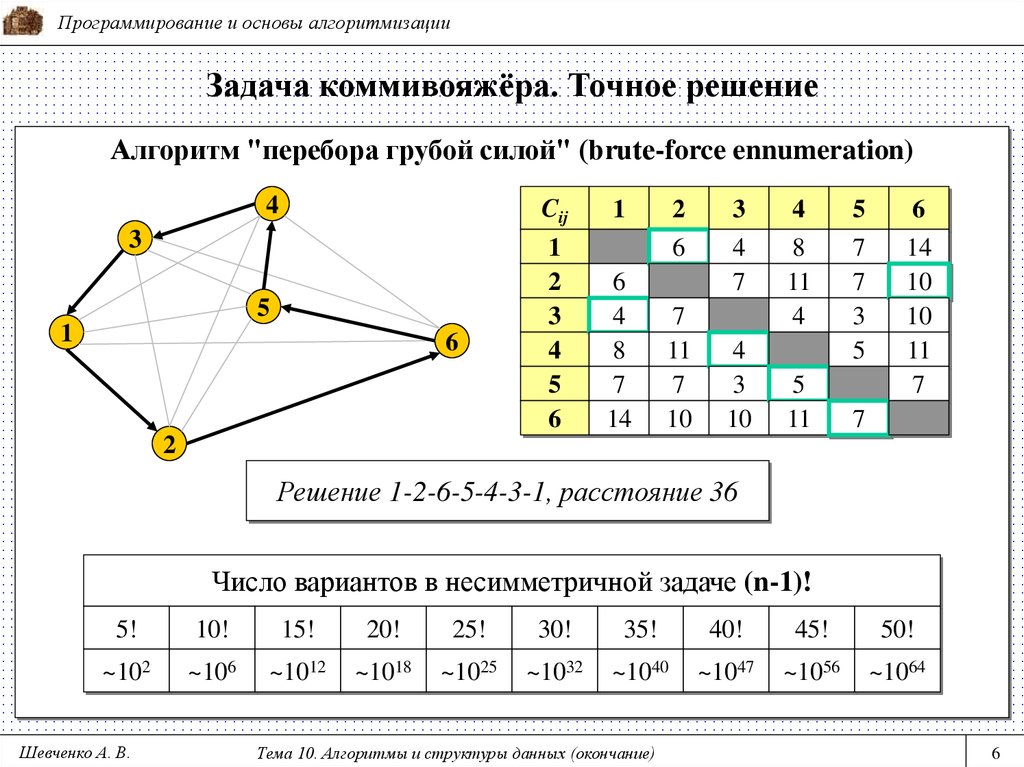
6. Задача коммивояжёра. Точное решение

Программирование и основы алгоритмизации
Задача коммивояжёра. Точное решение
Алгоритм "перебора грубой силой" (brute-force ennumeration)
4
3
5
1
6
Cij
1
1
2
3
4
5
6
6
4
8
7
14
2
6
7
11
7
10
3
4
7
4
3
10
4
8
11
4
5
11
5
7
7
3
5
6
14
10
10
11
7
7
2
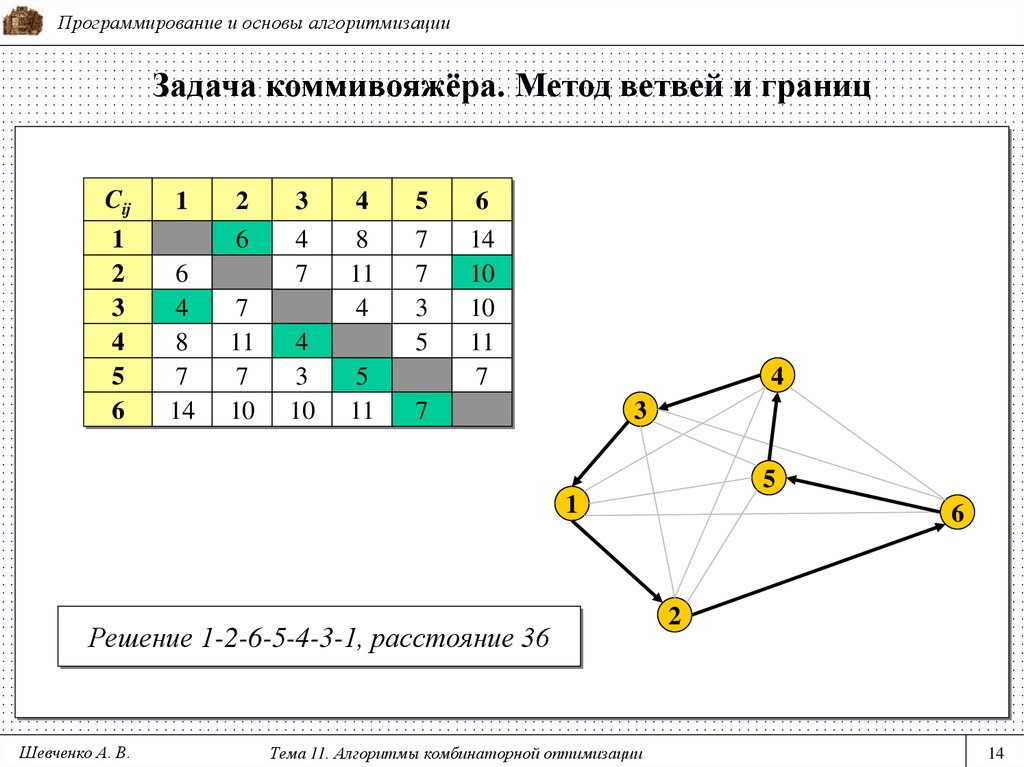
Решение 1-2-6-5-4-3-1, расстояние 36
Число вариантов в несимметричной задаче (n-1)!
5!
10!
15!
20!
25!
30!
35!
40!
45!
50!
~102
~106
~1012
~1018
~1025
~1032
~1040
~1047
~1056
~1064
Шевченко А. В.
Тема 10. Алгоритмы и структуры данных (окончание)
6

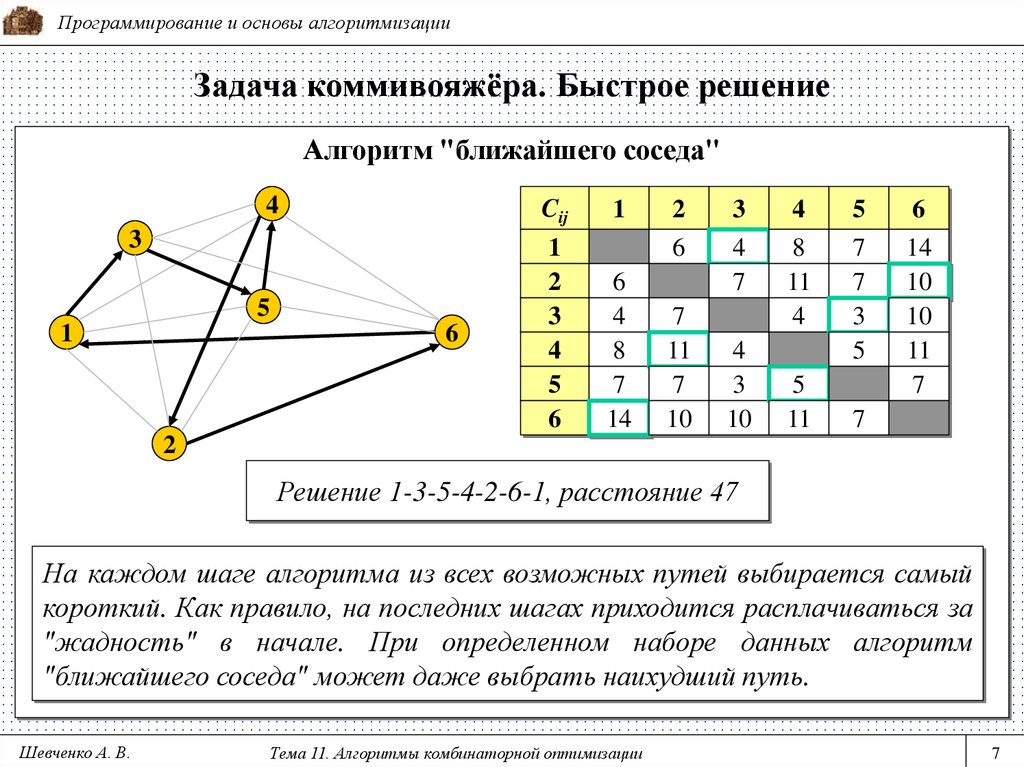
7. Задача коммивояжёра. Быстрое решение

Программирование и основы алгоритмизации
Задача коммивояжёра. Быстрое решение
Алгоритм "ближайшего соседа"
4
3
5
1
6
Cij
1
1
2
3
4
5
6
6
4
8
7
14
2
6
7
11
7
10
3
4
7
4
3
10
4
8
11
4
5
11
5
7
7
3
5
6
14
10
10
11
7
7
2
Решение 1-3-5-4-2-6-1, расстояние 47
На каждом шаге алгоритма из всех возможных путей выбирается самый
короткий. Как правило, на последних шагах приходится расплачиваться за
"жадность" в начале. При определенном наборе данных алгоритм
"ближайшего соседа" может даже выбрать наихудший путь.
Шевченко А. В.
Тема 11. Алгоритмы комбинаторной оптимизации
7

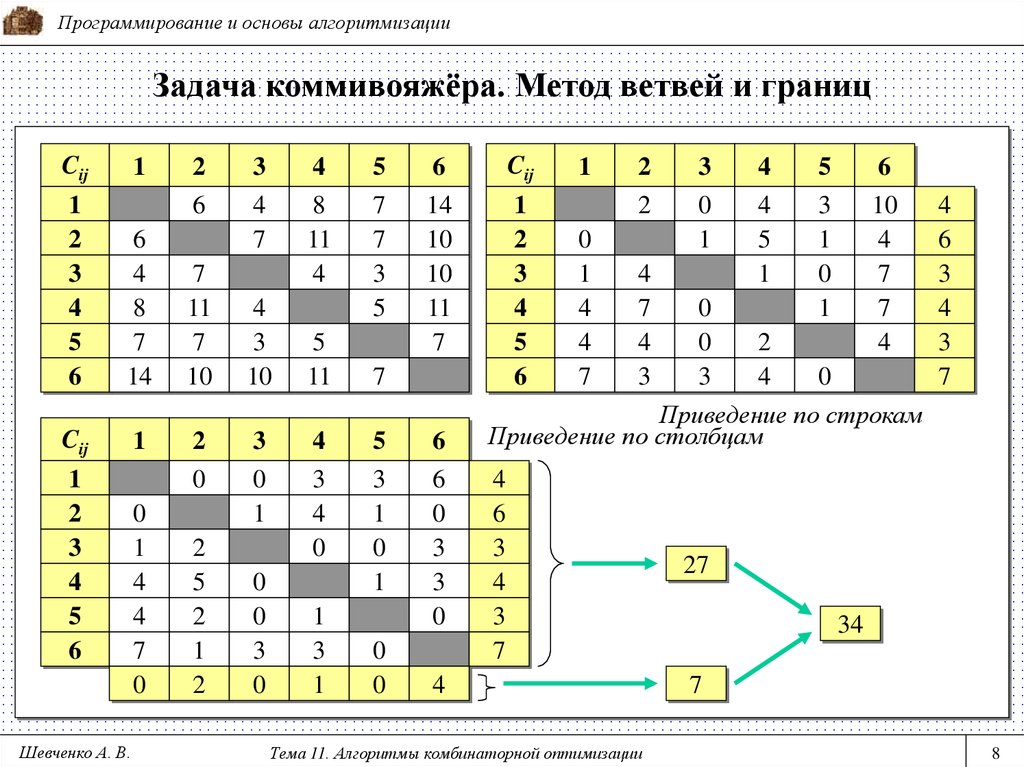
8. Задача коммивояжёра. Метод ветвей и границ

Программирование и основы алгоритмизации
Задача коммивояжёра. Метод ветвей и границ
Cij
1
1
2
3
4
5
6
6
4
8
7
14
Cij
1
1
2
3
4
5
6
Шевченко А. В.
0
1
4
4
7
0
2
6
7
11
7
10
2
0
2
5
2
1
2
3
4
7
4
8
11
4
4
3
10
3
0
1
0
0
3
0
5
11
4
3
4
0
1
3
1
5
7
7
3
5
6
14
10
10
11
7
7
5
3
1
0
1
0
0
6
6
0
3
3
0
Cij
1
2
3
4
5
6
1
0
1
4
4
7
2
2
3
0
1
4
7
4
3
4
4
5
1
5
3
1
0
1
6
10
4
7
7
4
0
0
2
3
4
0
Приведение по строкам
Приведение по столбцам
4
6
3
4
3
7
4
Тема 11. Алгоритмы комбинаторной оптимизации
4
6
3
4
3
7
27
34
7
8

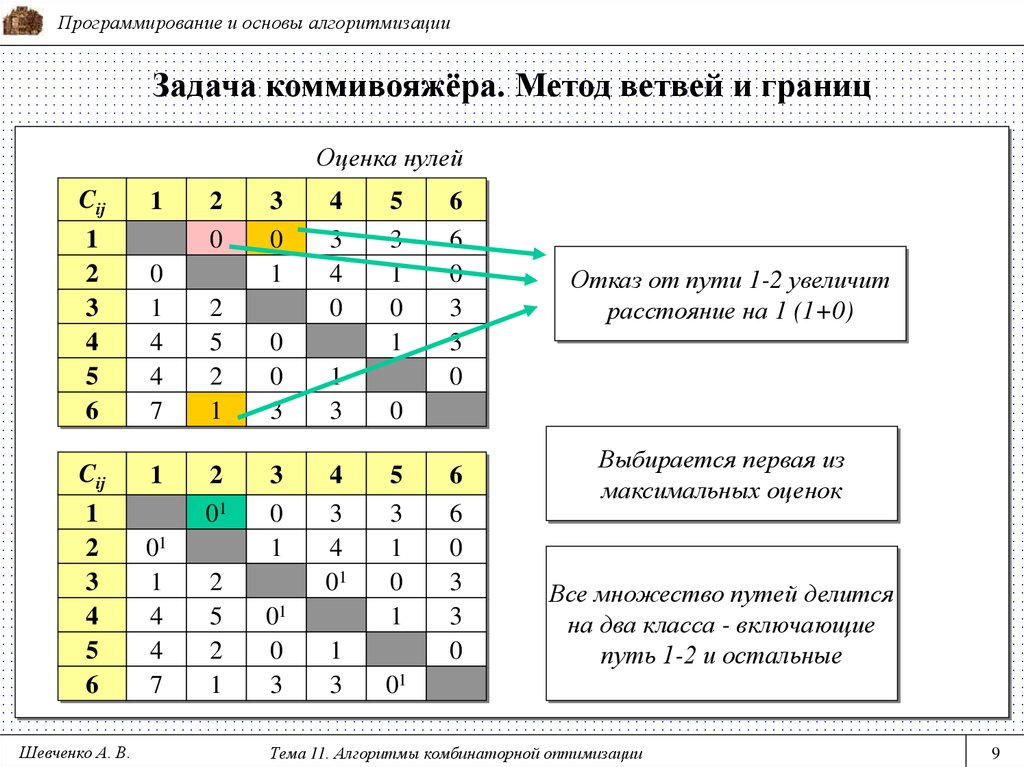
9. Задача коммивояжёра. Метод ветвей и границ

Программирование и основы алгоритмизации
Задача коммивояжёра. Метод ветвей и границ
Оценка нулей
Cij
1
1
2
3
4
5
6
0
1
4
4
7
Cij
1
1
2
3
4
5
6
01
1
4
4
7
Шевченко А. В.
2
0
2
5
2
1
2
01
2
5
2
1
3
0
1
0
0
3
3
0
1
4
3
4
0
1
3
4
3
4
01
01
0
3
1
3
5
3
1
0
1
6
6
0
3
3
0
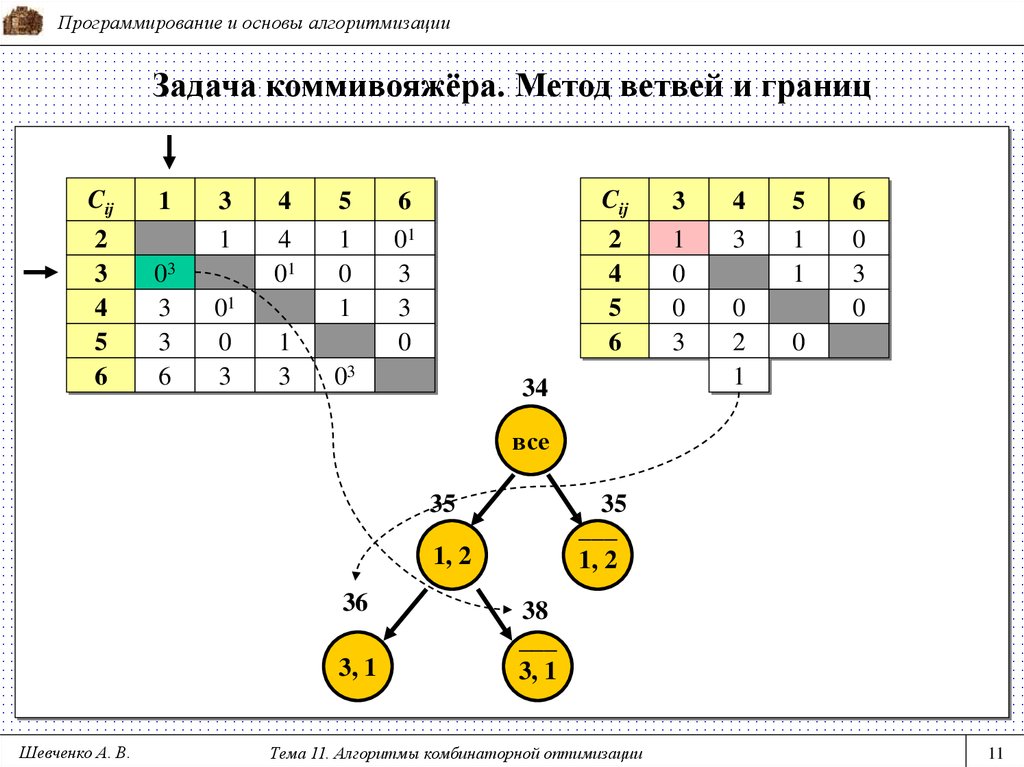
Отказ от пути 1-2 увеличит
расстояние на 1 (1+0)
0
5
3
1
0
1
6
6
0
3
3
0
Выбирается первая из
максимальных оценок
Все множество путей делится
на два класса - включающие
путь 1-2 и остальные
01
Тема 11. Алгоритмы комбинаторной оптимизации
9

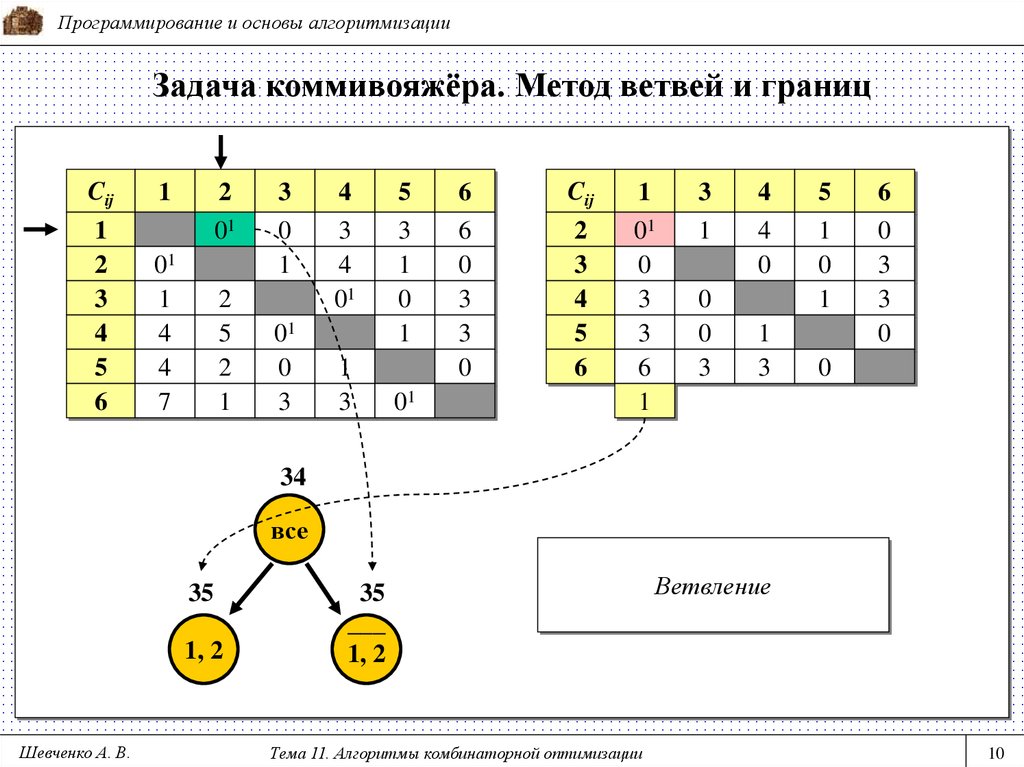
10. Задача коммивояжёра. Метод ветвей и границ

Программирование и основы алгоритмизации
Задача коммивояжёра. Метод ветвей и границ
Cij
1
2
3
4
5
6
1
01
1
4
4
7
2
3
4
5
6
Cij
1
3
4
5
6
01
0
1
3
4
01
3
1
0
1
6
0
3
3
0
2
3
4
5
6
01
0
3
3
6
1
1
4
0
1
0
1
0
3
3
0
2
5
2
1
01
0
3
1
3
01
0
0
3
1
3
0
34
все
35
1, 2
Шевченко А. В.
35
___
1, 2
Тема 11. Алгоритмы комбинаторной оптимизации
Ветвление
10

11. Задача коммивояжёра. Метод ветвей и границ

Программирование и основы алгоритмизации
Задача коммивояжёра. Метод ветвей и границ
Cij
2
3
4
5
6
1
03
3
3
6
3
1
01
0
3
4
4
01
1
3
5
1
0
1
Cij
6
01
3
3
0
2
4
5
6
03
34
3
1
0
0
3
4
3
0
2
1
5
1
1
6
0
3
0
0
все
35
35
___
1, 2
1, 2
36
3, 1
Шевченко А. В.
38
___
3, 1
Тема 11. Алгоритмы комбинаторной оптимизации
11

12. Задача коммивояжёра. Метод ветвей и границ

Программирование и основы алгоритмизации
Задача коммивояжёра. Метод ветвей и границ
34
Cij
2
4
5
6
3
01
0
3
4
5
6
3
1
1
01
3
0
02
2
все
35
1, 2
36
03
38
___
3, 1
3, 1
Cij
3
2
4
5
03
Cij
4
5
4
3
0
03
3
0
4
6
06
3
36
39
___
6, 5
6, 5
36
2, 6
39
___
2, 6
36
5, 4
0
35
___
1, 2
36
Конец ветви
4, 3
Шевченко А. В.
Тема 11. Алгоритмы комбинаторной оптимизации
12

13. Задача коммивояжёра. Метод ветвей и границ

Программирование и основы алгоритмизации
Задача коммивояжёра. Метод ветвей и границ
Cij
1
2
3
4
5
6
1
2
3
4
5
6
34
01
03
1
3
4
01
3
1
0
1
6
0
3
3
0
все
01
1
4
4
7
2
5
2
1
01
0
3
1
3
35
___
1, 2
36
01
1, 3
Cij
2
3
4
5
6
Шевченко А. В.
1
0
1
4
4
7
2
1
4
1
0
1
4
4
0
1
3
5
1
0
1
0
6
0
3
3
0
38
___
1, 3
Проверка альтернативных
вариантов
Тема 11. Алгоритмы комбинаторной оптимизации
13

14. Задача коммивояжёра. Метод ветвей и границ

Программирование и основы алгоритмизации
Задача коммивояжёра. Метод ветвей и границ
Cij
1
1
2
3
4
5
6
6
4
8
7
14
2
6
7
11
7
10
3
4
7
4
3
10
4
8
11
4
5
11
5
7
7
3
5
6
14
10
10
11
7
4
7
3
5
1
Решение 1-2-6-5-4-3-1, расстояние 36
Шевченко А. В.
Тема 11. Алгоритмы комбинаторной оптимизации
6
2
14

15. Динамическое программирование

Программирование и основы алгоритмизации
Динамическое программирование
Метод динамического программирования состоит в том, что
оптимальное управление строится постепенно. На каждом шаге оптимизируется
управление только этого шага. Вместе с тем на каждом шаге управление
выбирается с учетом последствий, так как управление, оптимизирующее целевую
функцию только для данного шага, может привести к неоптимальному эффекту
всего процесса. Управление на каждом шаге должно быть оптимальным с точки
зрения процесса в целом.
Каково бы ни было начальное состояние системы перед очередным
шагом, управление на этом этапе выбирается так, чтобы выигрыш на данном шаге
плюс оптимальный выигрыш на всех последующих шагах был максимальным.
Ричард Эрнст Беллман (1920 - 1984)
Шевченко А. В.
Тема 11. Алгоритмы комбинаторной оптимизации
15

16. Пример задачи динамического программирования

Программирование и основы алгоритмизации
Пример задачи динамического программирования
Оптимизация последовательности работ
штамповочной машины Strippit-1250
Шевченко А. В.
Тема 11. Алгоритмы комбинаторной оптимизации
16

17. Схема работы машины

Программирование и основы алгоритмизации
Схема работы машины
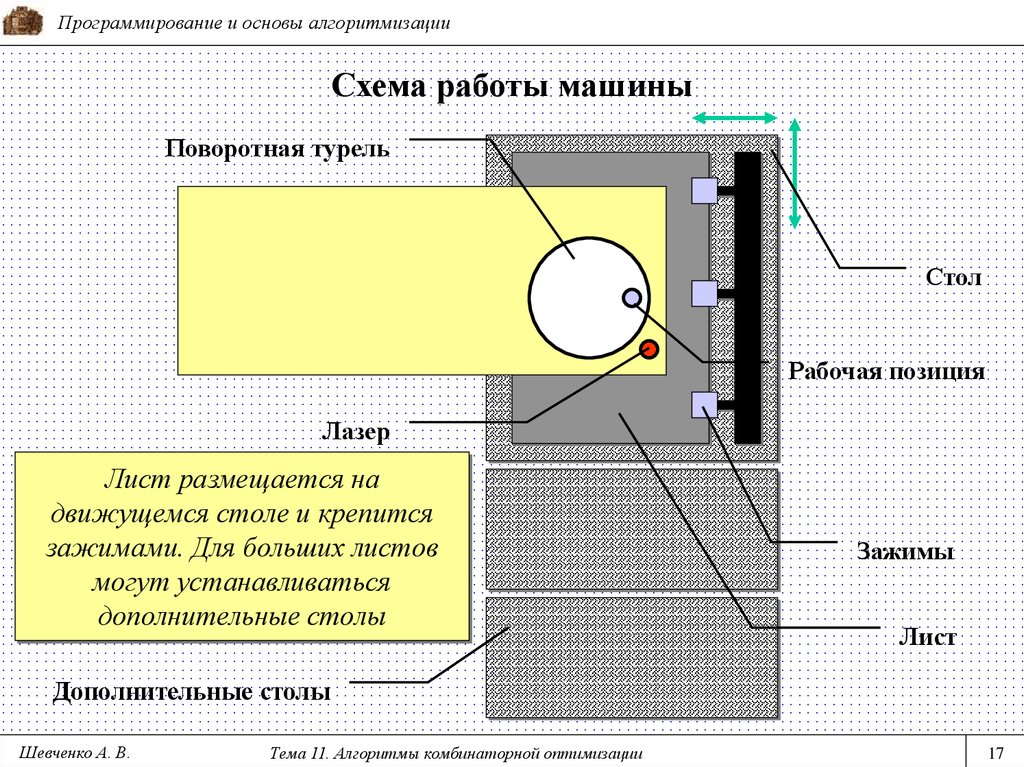
Поворотная турель
Стол
Рабочая позиция
Лазер
Лист размещается на
движущемся столе и крепится
зажимами. Для больших листов
могут устанавливаться
дополнительные столы
Зажимы
Лист
Дополнительные столы
Шевченко А. В.
Тема 11. Алгоритмы комбинаторной оптимизации
17

18. Пробивной инструмент

Программирование и основы алгоритмизации
Пробивной инструмент
Пуансон
Лист
Зазор
Матрица
Для пробивки отверстий используется пара инструментов - пуансон и
матрица. Для одного пуансона могут применяться разные матрицы.
Выбор матрицы зависит от толщины листа. Чем толще лист, тем
больше должен быть зазор между пуансоном и матрицей.
Шевченко А. В.
Тема 11. Алгоритмы комбинаторной оптимизации
18

19. Поворотная турель

Программирование и основы алгоритмизации
Поворотная турель
Пробивной инструмент (пуансоны и матрицы) устанавливается в
поворотную турель, имеющую 20 станций (16 нормальных и 4 большие)
Шевченко А. В.
Тема 11. Алгоритмы комбинаторной оптимизации
19

20. Задача оптимизации последовательности заданий

Программирование и основы алгоритмизации
Задача оптимизации последовательности заданий
Задание
В малосерийном производстве через
штамповочную машину за день проходит
до 50 партий изделий (заданий). Для
каждого задания требуется установка в
турель от 1 до 19 инструментов. Для
минимизации общего времени производства
требуется
подобрать такую
последовательность выполнения заданий,
при которой время смены инструмента
было бы минимальным.
Шевченко А. В.
Общее время производства
Выполнение
программы
Тема 11. Алгоритмы комбинаторной оптимизации
Смена
инструмента
20

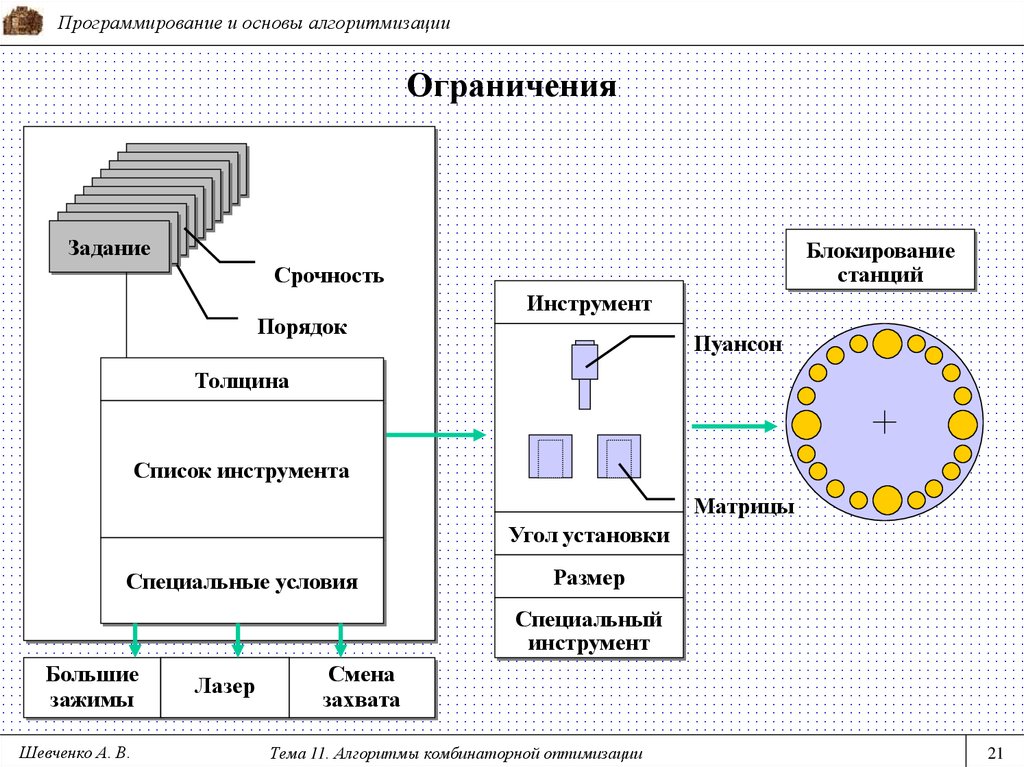
21. Ограничения

Программирование и основы алгоритмизации
Ограничения
Задание
Блокирование
станций
Срочность
Порядок
Инструмент
Пуансон
Толщина
Список инструмента
Матрицы
Угол установки
Специальные условия
Размер
Специальный
инструмент
Большие
зажимы
Шевченко А. В.
Лазер
Смена
захвата
Тема 11. Алгоритмы комбинаторной оптимизации
21

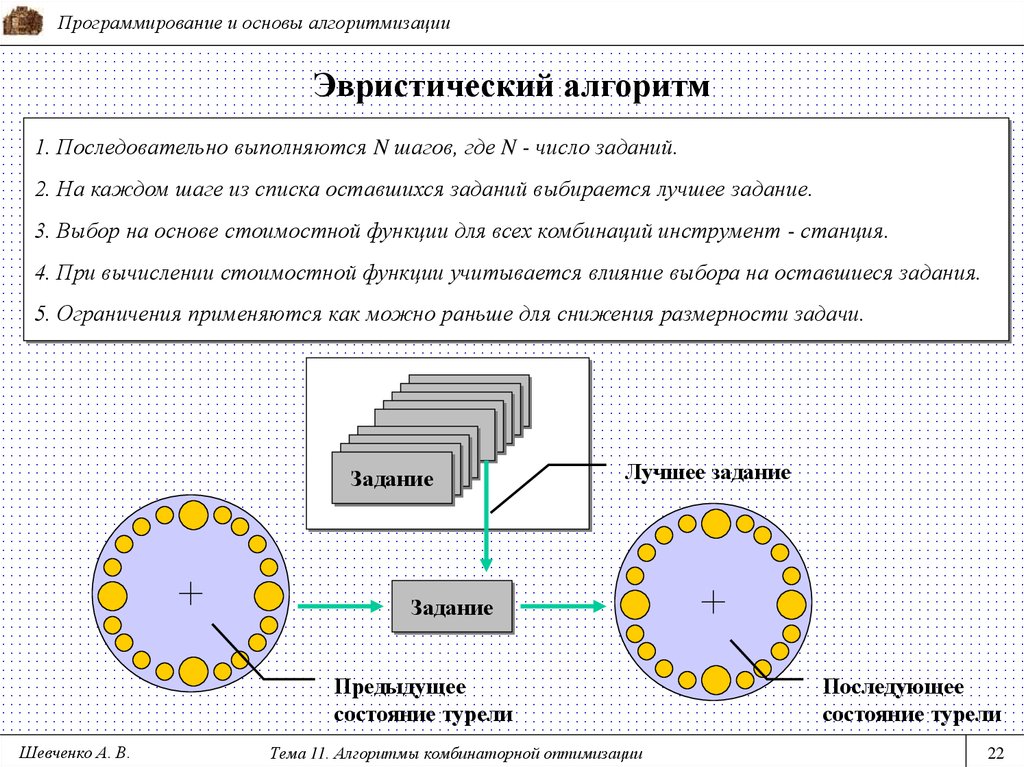
22. Эвристический алгоритм

Программирование и основы алгоритмизации
Эвристический алгоритм
1. Последовательно выполняются N шагов, где N - число заданий.
2. На каждом шаге из списка оставшихся заданий выбирается лучшее задание.
3. Выбор на основе стоимостной функции для всех комбинаций инструмент - станция.
4. При вычислении стоимостной функции учитывается влияние выбора на оставшиеся задания.
5. Ограничения применяются как можно раньше для снижения размерности задачи.
Задание
Лучшее задание
Задание
Предыдущее
состояние турели
Шевченко А. В.
Тема 11. Алгоритмы комбинаторной оптимизации
Последующее
состояние турели
22

23. Учет ограничений

Программирование и основы алгоритмизации
Учет ограничений
Задания
1
2
3
4
5
Станции
6
7
Большой инструмент
8
Малый инструмент
Угол 0°
Угол 45°
Угол 90°
3 и 5 - срочные задания
Специальный инструмент
6 перед 2
7 перед 6
Шевченко А. В.
Тема 11. Алгоритмы комбинаторной оптимизации
23

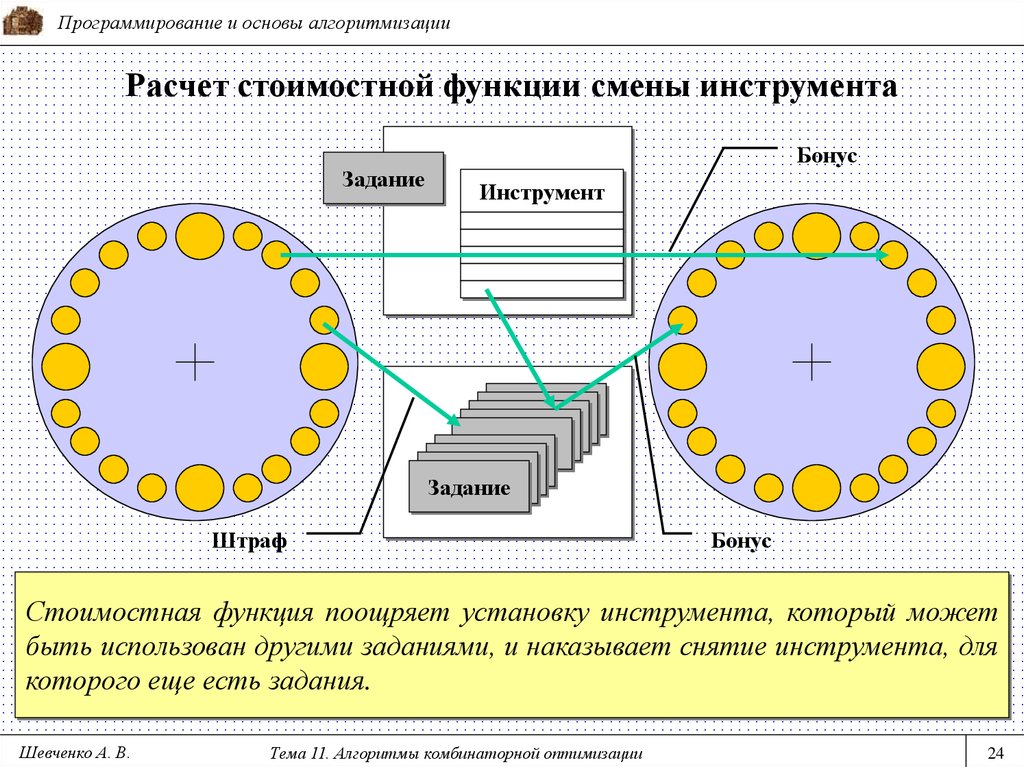
24. Расчет стоимостной функции смены инструмента

Программирование и основы алгоритмизации
Расчет стоимостной функции смены инструмента
Задание
Бонус
Инструмент
Задание
Штраф
Бонус
Стоимостная функция поощряет установку инструмента, который может
быть использован другими заданиями, и наказывает снятие инструмента, для
которого еще есть задания.
Шевченко А. В.
Тема 11. Алгоритмы комбинаторной оптимизации
24

25. Пример стоимостной функции для 8 инструментов

Программирование и основы алгоритмизации
Пример стоимостной функции для 8 инструментов
Станции
1
И1
2
3
4
5
6
7
8
9
10 11 12 13 14 15 16 17 18 19 20
-60
44
И2
-40
36
И3
40 42 42 40
42 44 44 42
40 42 42 42
40
И4
40 42 42 42
40 42 42 42
40 44 -20 44
42 40 40 44
И5
46 44
28 42
36 42
40 40
32
И6
28
48 42
42
И7
44 42 48
44 -60 46
42 42 40
42 40 44
И8
42 42 42 44
42 44 44 42
46 42 42 44
42 44 44 44
Ищется вариант размещения инструментов, который
даст минимальное значение стоимостной функции
Шевченко А. В.
Тема 11. Алгоритмы комбинаторной оптимизации
25

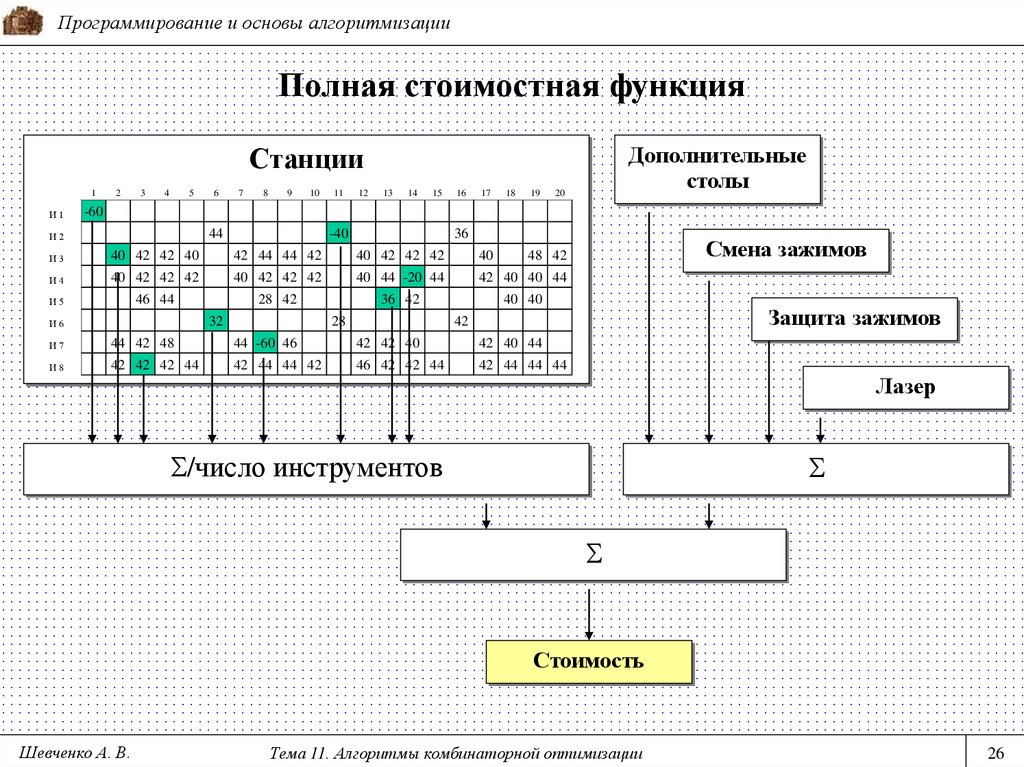
26. Полная стоимостная функция

Программирование и основы алгоритмизации
Полная стоимостная функция
Дополнительные
столы
Станции
1
И1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
-60
44
И2
-40
36
И3
40 42 42 40
42 44 44 42
40 42 42 42
40
И4
40 42 42 42
40 42 42 42
40 44 -20 44
42 40 40 44
И5
46 44
28 42
36 42
40 40
32
И6
28
Смена зажимов
48 42
Защита зажимов
42
И7
44 42 48
44 -60 46
42 42 40
42 40 44
И8
42 42 42 44
42 44 44 42
46 42 42 44
42 44 44 44
Лазер
/число инструментов
Стоимость
Шевченко А. В.
Тема 11. Алгоритмы комбинаторной оптимизации
26

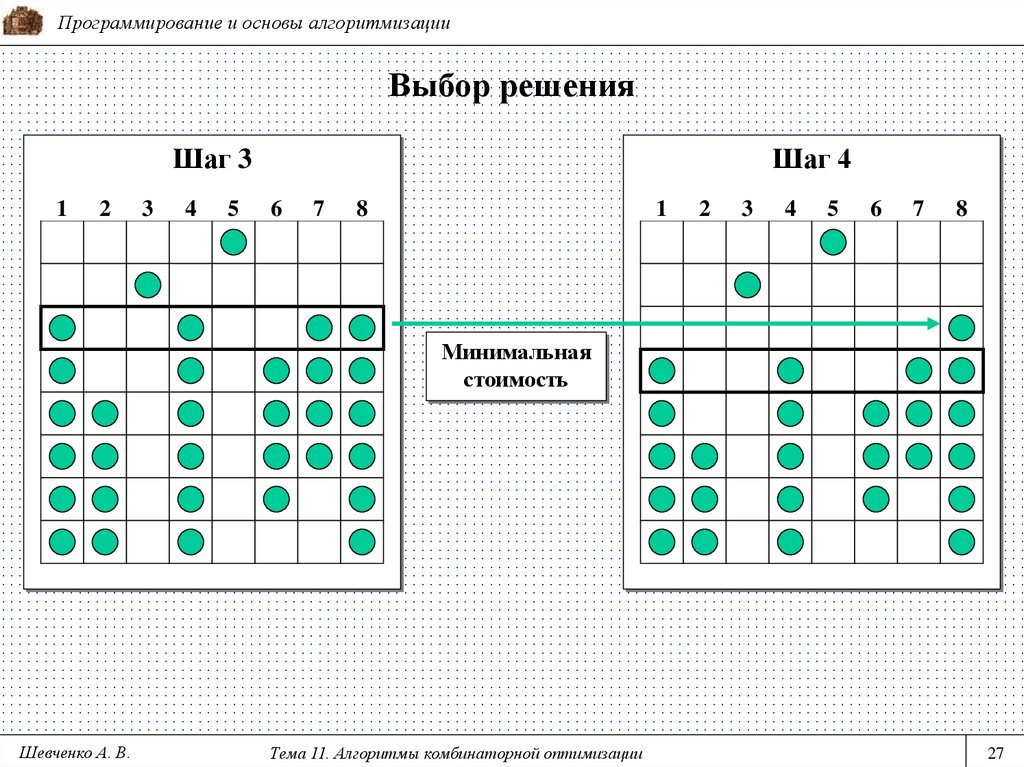
27. Выбор решения

Программирование и основы алгоритмизации
Выбор решения
Шаг 3
1
2
3
4
5
Шаг 4
6
7
8
1
2
3
4
5
6
7
8
Минимальная
стоимость
Шевченко А. В.
Тема 11. Алгоритмы комбинаторной оптимизации
27

28. Результаты оптимизации

Программирование и основы алгоритмизации
Результаты оптимизации
INIT STATE-------------------------------------------------------------------------------Punch [
0 287 292 281 35 302 316 302 44 81 17 316 45 249 14 133 169 323 281 275 ]
Matrix [
0 459 476 442 28 507 535 495 37 78 15 535 43 364
8 134 206 550 442 423 ]
Angle [
0 90
0
0 90
0
0
0
0
0 90
0 90
0
0
0
0 45
0
0 ]
0: 0
0: 0
RETOOLING--------------------------------------------------------------------------------Punch [ 287 91 40 281 138 316 323 302 44 289 17 316 45 249 14 133 169 281 281 275 ]
Matrix [ 458 85 35 442 142 531 548 495 37 463 15 535 43 364
8 134 206 440 442 423 ]
Angle [
0
0
0
0
0 90
0
0
0 90 90
0 90
0
0
0
0 45
0
0 ]
2: 6
2: 6
Job
Job
Job
Job
Job
Job
Job
Job
Job
15
14
16
17
18
19
20
4
3
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
RETOOLING--------------------------------------------------------------------------------Punch [ 287 91 40 281 138 316 323 302 44 60 316 139
6 17 14 133 54 297 302 275 ]
Matrix [ 458 85 35 440 142 531 548 495 37 53 531 143
2 10
8 134 47 484 495 423 ]
Angle [
0
0
0
0
0 90
0
0
0
0
0
0
0
0
0
0
0
0 90
0 ]
Job
Job
1
2
Шевченко А. В.
*
*
*
*
*
*
*
*
*
*
Тема 11. Алгоритмы комбинаторной оптимизации
1: 7
1: 8
*
*
*
28

29. Результаты оптимизации

Программирование и основы алгоритмизации
Результаты оптимизации
RETOOLING--------------------------------------------------------------------------------Punch [ 287 91 40 281 138 316 323 302 44 60 316 139
6 110 14 133 54 297 302 275 ]
Matrix [ 458 85 35 440 142 535 550 495 37 53 535 143
2 111
8 134 47 484 495 423 ]
Angle [
0
0
0
0
0 90
0
0
0
0
0
0
0
0
0
0
0
0 90
0 ]
Job 13
*
*
*
*
RETOOLING--------------------------------------------------------------------------------Punch [ 287 91 40 281 138 316 323 302 44 60 316 139
1 110 14 169 155 35 302 275 ]
Matrix [ 458 85 33 440 142 531 550 495 37 53 531 143
2 111
8 206 172 28 495 423 ]
Angle [
0
0
0
0
0 90
0
0
0
0
0
0
0
0
0
0
0
0 90
0 ]
Job 5
Job 6
Job 7
Job 21
Job 28
Job 27
8
9
10
11
12
25
24
23
1: 3
3: 3
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
RETOOLING--------------------------------------------------------------------------------Punch [ 287 91 40 281 249 163 323 302 70 60 316 139
1 25 14 169 155 35 302 133 ]
Matrix [ 459 85 33 440 364 191 549 495 66 53 531 143
1 21
8 206 173 28 495 134 ]
Angle [
0
0
0
0 90
0
0
0
0
0
0
0
0
0
0
0
0
0 90
0 ]
Job
Job
Job
Job
Job
Job
Job
Job
0: 1
2: 2
1: 4
2: 7
*
*
*
*
*
*
*
*
*
Шевченко А. В.
*
*
*
*
*
*
Тема 11. Алгоритмы комбинаторной оптимизации
*
29

30. Результаты оптимизации

Программирование и основы алгоритмизации
Результаты оптимизации
RETOOLING--------------------------------------------------------------------------------Punch [ 287 91 40 281 249 163 323 302 70 60 316 139
1 25 14 169 155 35 302 133 ]
Matrix [ 459 85 33 440 364 191 548 495 66 53 531 143
1 21
8 206 173 28 495 134 ]
Angle [
0
0
0
0 90
0
0
0
0
0
0
0
0
0
0
0
0
0 90
0 ]
Job 22
*
*
RETOOLING--------------------------------------------------------------------------------Punch [ 287 64 40 36 26 163 323 264 70 60 284 139
1 45 114 169 155 35 102 107 ]
Matrix [ 459 63 33 36 26 191 551 406 66 59 453 143
1 45 115 206 174 28 104 108 ]
Angle [
0
0
0
0
0
0
0 90
0
0
0
0
0
0
0
0
0
0
0
0 ]
Job 33
Job 30
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
Шевченко А. В.
*
*
*
*
*
*
*
*
*
*
1: 4
1: 5
*
*
RETOOLING--------------------------------------------------------------------------------Punch [ 287 120 40 36 105 311 323 127 91 144 284 139
1 45 97 311 51 157 321 112 ]
Matrix [ 459 120 39 36 106 523 551 127 88 153 453 145
1 45 98 523 50 177 546 114 ]
Angle [
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0 90
0
0
0
0 ]
Job 29
Job 26
1: 8
1:11
*
RETOOLING--------------------------------------------------------------------------------Punch [ 287 120 40 36 26 164 323 264 91 144 284 139
1 45 114 169 51 35 102 107 ]
Matrix [ 459 120 33 36 26 195 551 406 88 153 453 143
1 45 115 206 50 35 104 108 ]
Angle [
0
0
0
0
0
0
0 90
0
0
0
0
0
0
0
0
0
0
0
0 ]
Job 31
Job 34
Job 32
0: 0
0: 1
*
*
*
2: 6
2: 8
*
*
Тема 11. Алгоритмы комбинаторной оптимизации
30