Векторы плоскости

1. Тема: «Векторы плоскости»

Выполнил: Календарев Равиль 9 «Г»

2. Определение вектора

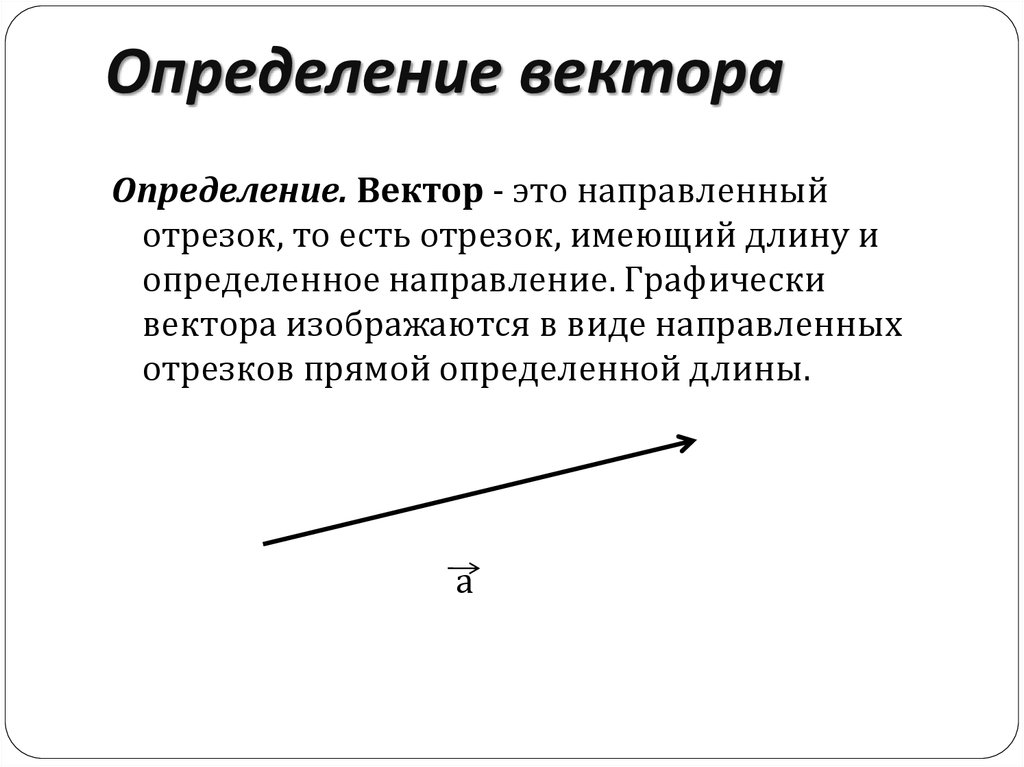
Определение. Вектор - это направленный
отрезок, то есть отрезок, имеющий длину и
определенное направление. Графически
вектора изображаются в виде направленных
отрезков прямой определенной длины.
а
A

3. Обозначение вектора

Вектор началом которого есть точка
А, а концом - точка В,
обозначается AB.Также вектора
обозначают одной маленькой буквой,
например a.
В
А
АВ

4. Длина вектора

Определение. Длина направленного отрезка
определяет числовое значение вектора и
называется длиной вектораили модулем
вектора AB.
Для обозначения длины вектора используются
две вертикальные линии слева и справа |AB|.

5. Нулевой вектор

Определение. Нулевым
вектором называется вектор, у которого
начальная и конечная точка совпадают.
Нулевой вектор обычно обозначается как 0.
Длина нулевого вектора равна нулю.
.0

6. Коллинеарные вектора

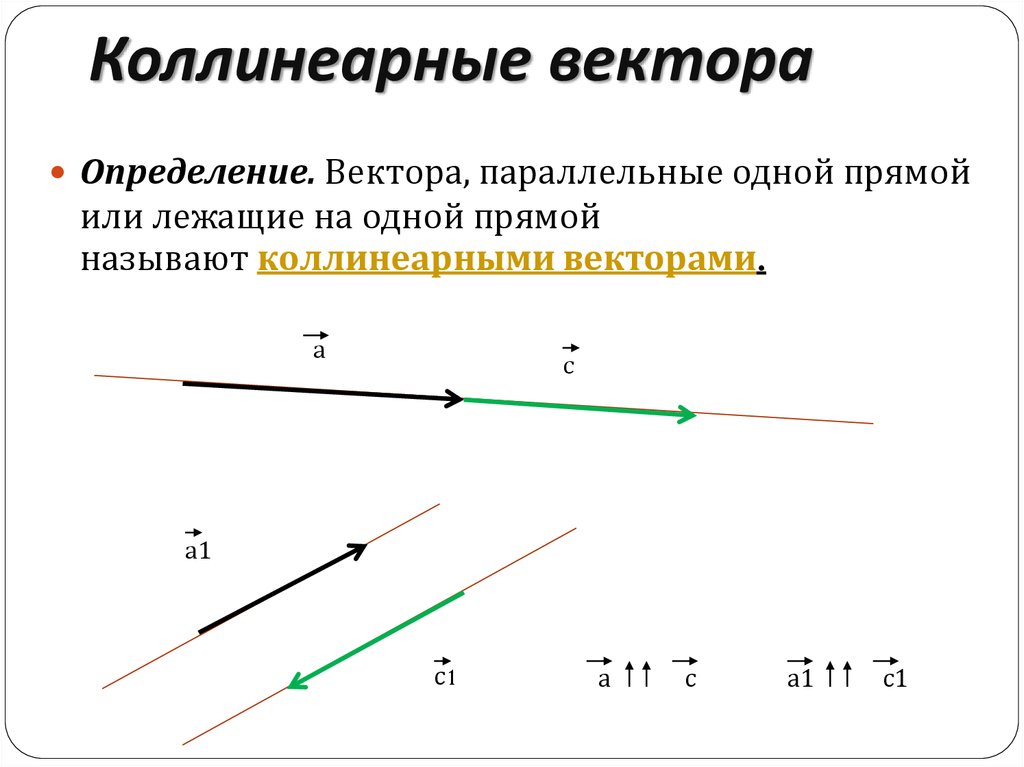
Определение. Вектора, параллельные одной прямой
или лежащие на одной прямой
называют коллинеарными векторами.
а
с
а1
с1
а
с
а1
с1

7. Сонаправленные вектора

Определение. Два коллинеарных
вектора a и b называются сонаправленными
векторами, если их направления
совпадают: a↑↑b
а
в

8. Противоположно направленные вектора

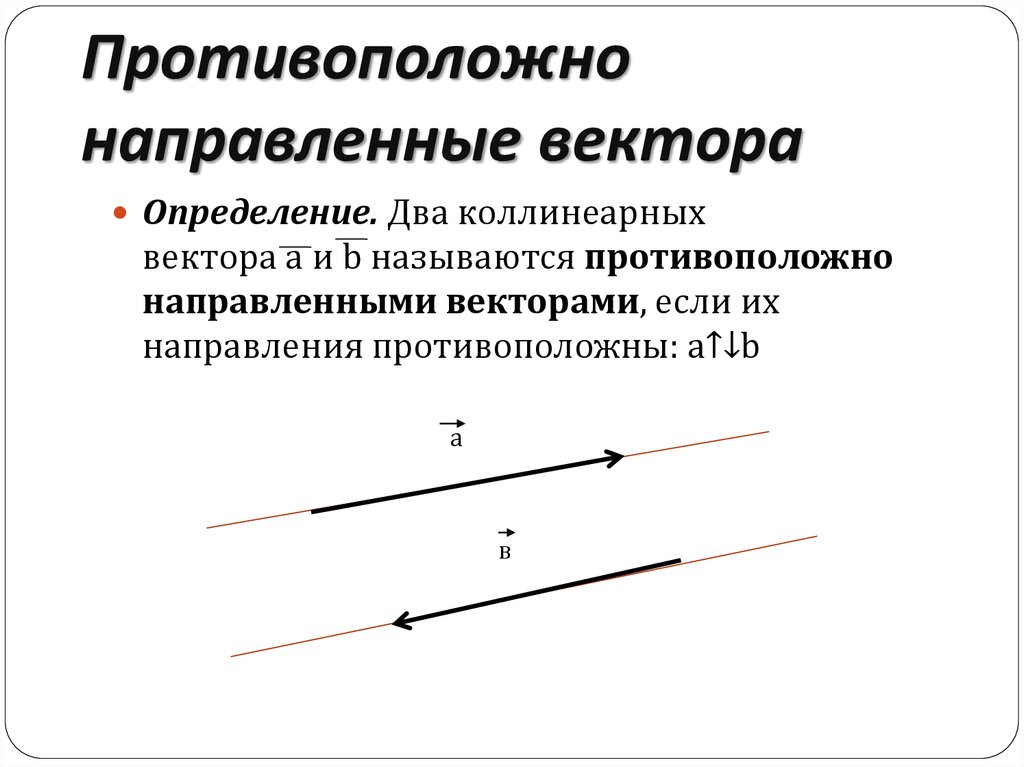
Определение. Два коллинеарных
вектора a и b называются противоположно
направленными векторами, если их
направления противоположны: a↑↓b
а
в

9. Равные вектора

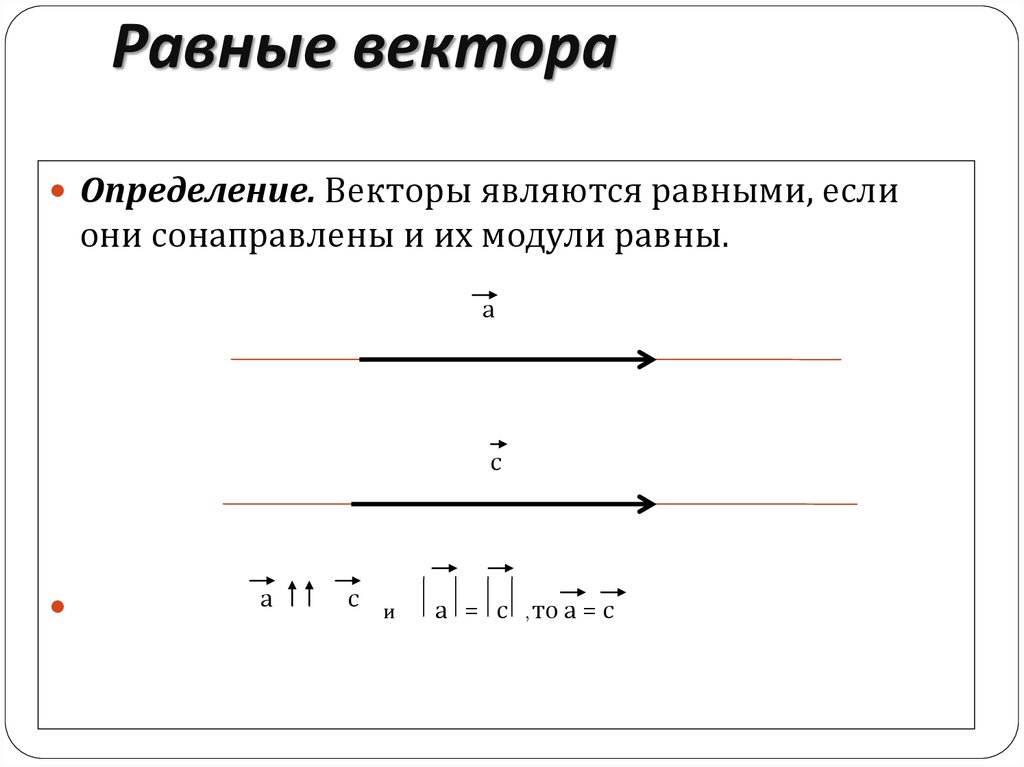
Определение. Векторы являются равными, если
они сонаправлены и их модули равны.
а
с
а
с
и
а = с ,то а = с

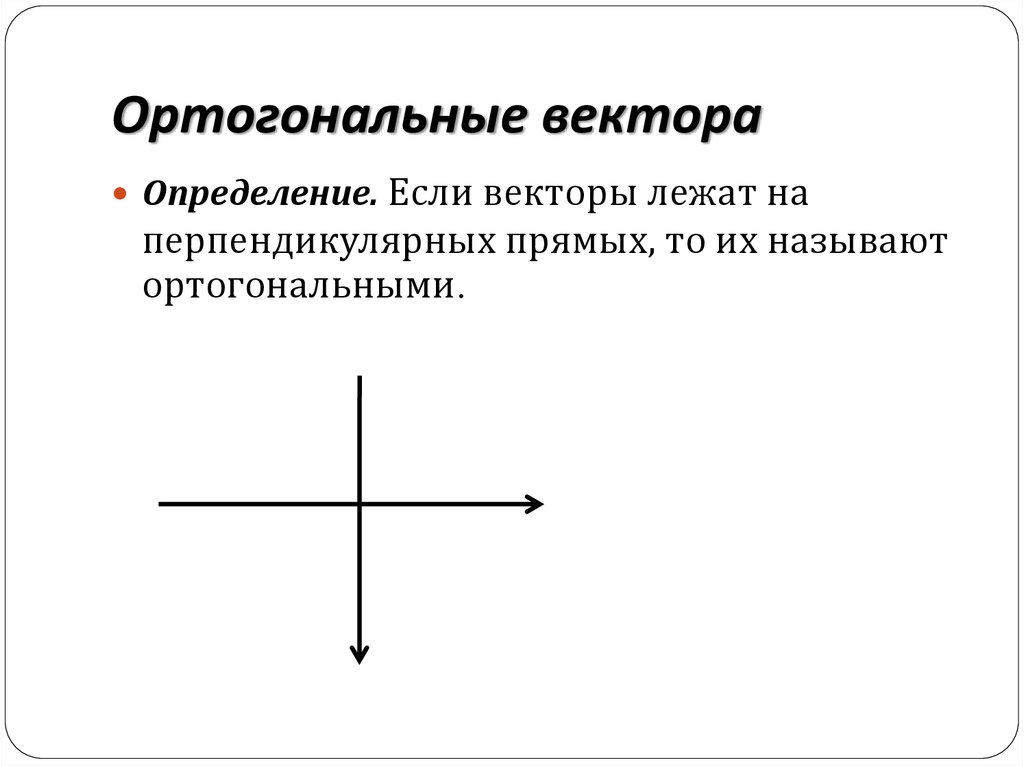
10. Ортогональные вектора

Определение. Если векторы лежат на
перпендикулярных прямых, то их называют
ортогональными.

11.  Сложение векторов по правилу параллелограмма

Сложение векторов по
правилу параллелограмма
Определение. Сложение векторных величин
производится по правилу параллелограмма:
сумма двух векторов а и в, приведенных к
общему началу, есть третий вектор с, длина
которого равна длине параллелограмма,
построенного на векторах а и в, а направлен
он от точки A к точке B

12.  Сложение векторов по правилу параллелограмма

Сложение векторов по правилу
параллелограмма
в
а

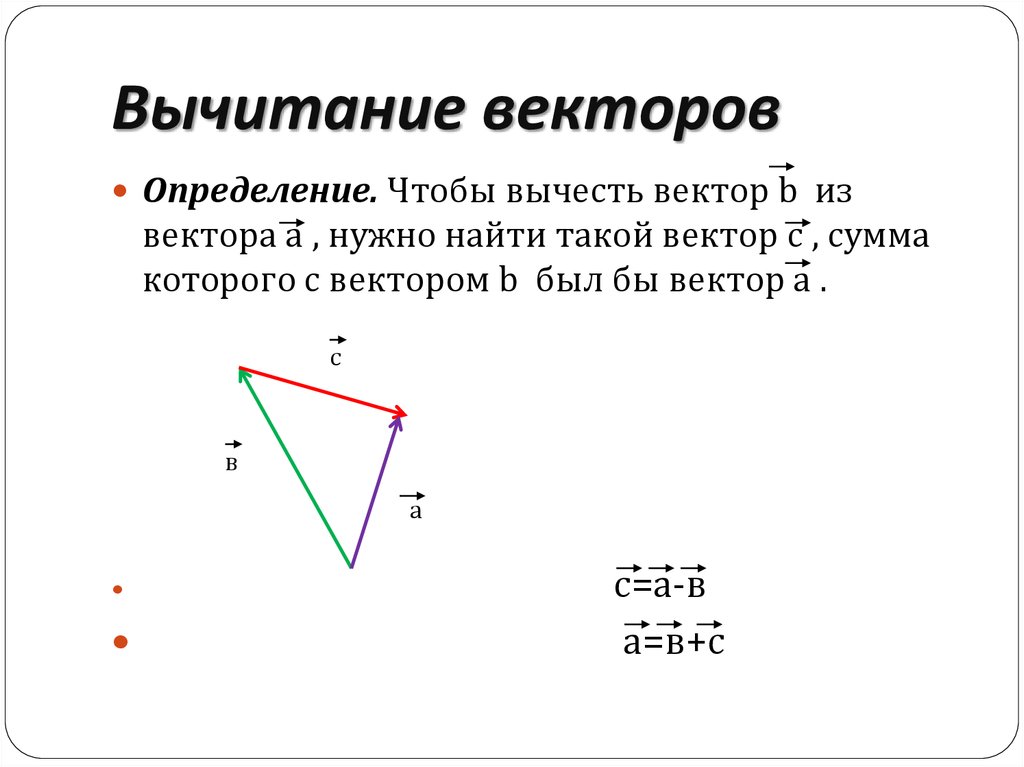
13. Вычитание векторов

Определение. Чтобы вычесть вектор b из
вектора a , нужно найти такой вектор c , сумма
которого с вектором b был бы вектор a .
с
в
а
с=а-в
а=в+с

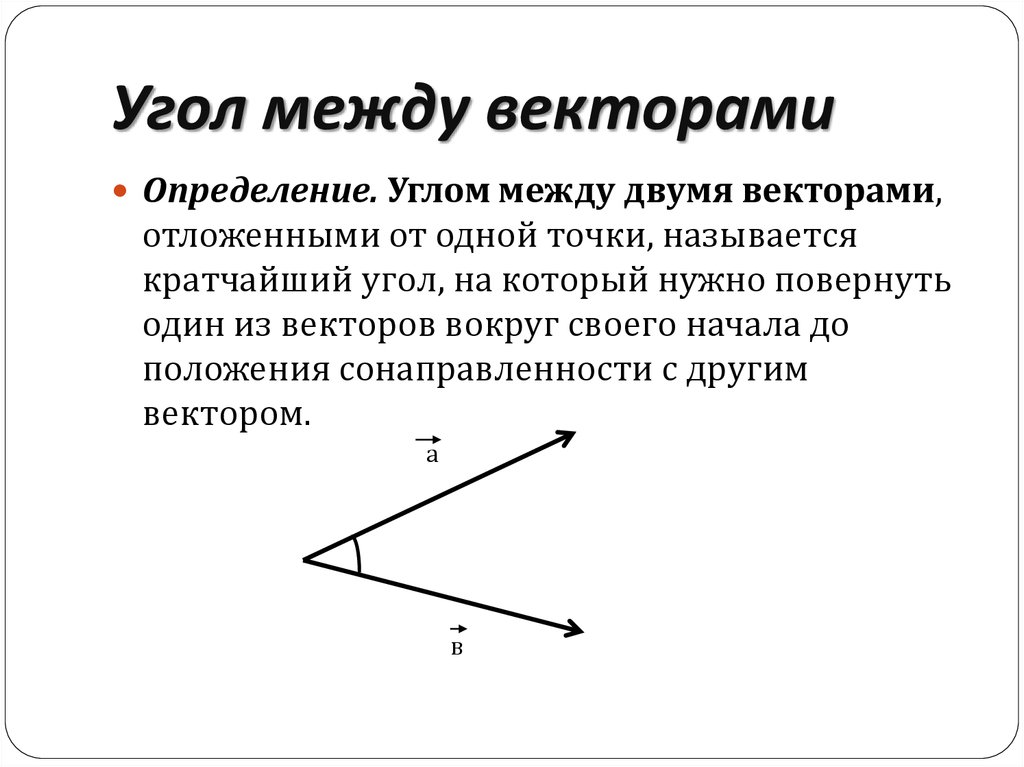
14. Угол между векторами

Определение. Углом между двумя векторами,
отложенными от одной точки, называется
кратчайший угол, на который нужно повернуть
один из векторов вокруг своего начала до
положения сонаправленности с другим
вектором.
а
в

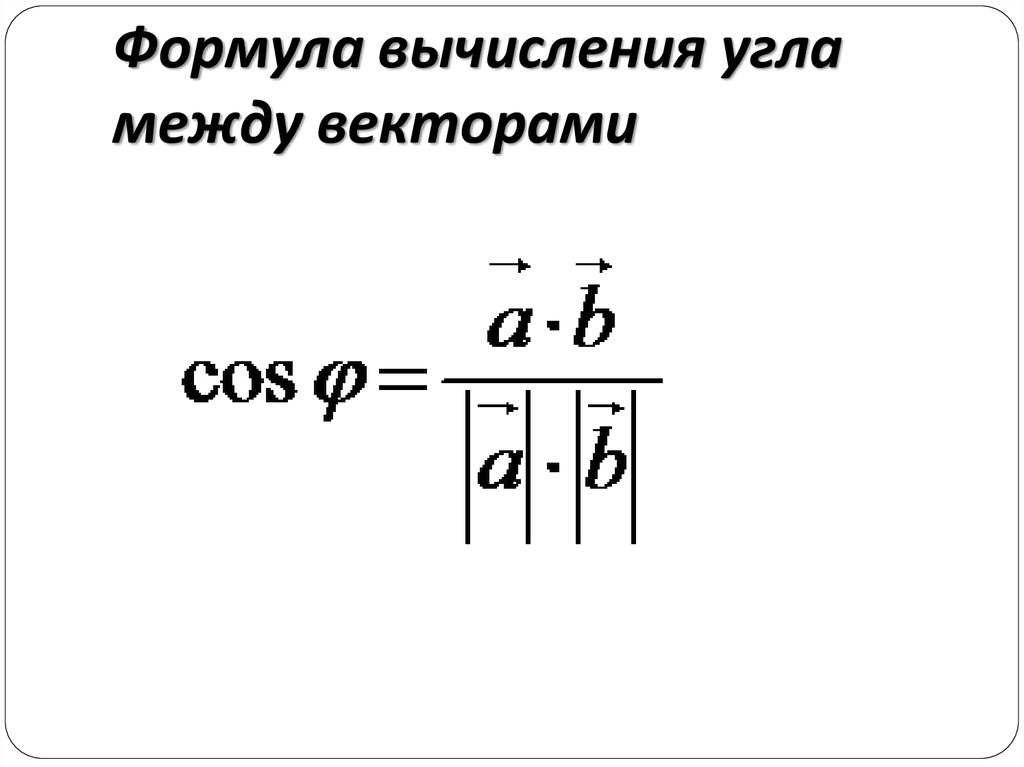
15. Формула вычисления угла между векторами

16. КООРДИНАТЫ ВЕКТОРА

Основное соотношение. Чтобы найти
координаты вектора AB, зная координаты его
начальной точек А и конечной точки В,
необходимо из координат конечной точки
вычесть соответствующие координаты
начальной точки.