Определение ряда и его суммы. (Лекция 2.15)

1. Лекция 2-15. 13. Ряды. 13.1. Числовые ряды. 13.1.1. Определение ряда и его суммы.

Пусть дана бесконечная последовательность
u1, u2 ,..., un ,... .
u1 + u2 + ... + un + ...
Определение. Выражение
называется рядом, а числа u1, u2 ,..., un ,...
- членами
ряда.
¥
Краткая запись
å un
n =1
.
un - общий член ряда.
Ряд считается заданным, если задана функция
un = f ( n ) .

2. Примеры

1
1 1
1
un = n Þ + + ... + n + ... .
2 4
2
2
1
1 1
1
un = Þ + + ... + + ... .
n! 1! 2!
n!
1)
2)
Иногда ряд задают рекуррентной формулой.
1
1
1
Пример. u1 = 1, u2 = , un = un -1 + un -2 .
2
1 1 1
7
,
Тогда u3 = × + × 1 =
2 2 3
12
2
и т.д.
3

3. Пусть дан ряд . Обозначим частичной суммой ряда.

u1 + u2 + ... + un + ...
Пусть дан ряд
.
Sn = u1 + u2 + ... + un
Обозначим
частичной суммой ряда.
Образуем последовательность частичных сумм
S1 = u1,
S2 = u1 + u2 , .............,
Sn = u1 + u2 + ... + un .
Определение. Если существует предел
lim Sn = S ,
последовательности { S n }
n®¥
S
то ряд сходящийся и
- его сумма.
Если последовательность { S n } не стремится к пределу,
то ряд расходящийся.
Последнее имеет место в двух случаях:
lim Sn = ¥;
1)
n®¥
2) не существует lim S n .
n®¥

4. Примеры:

¥
n
q
-1
n
,
1) å aq ( a ¹ 0, q < 1) ; Sn = a
q
1
n =1
qn - 1
a
lim Sn = a lim
=
= S.
1- q
n®¥ q - 1
¥ n®¥
2)
n
å aq ( a ¹ 0, q = 1) ; Sn = na, lim Sn = ¥.
n =1
3)
n®¥
¥
n
aq
å
( a ¹ 0,
q = -1) ;
n =1
S1 = - a, S2 = 0, S3 = - a, ...;
lim Sn
n®¥
не существует.

5. Свойства сходящихся рядов.

то сходится ряд
u1 + u2 + ... + un +сходится,
...
lu1 + lu2 + .... + lun + ...
Доказательство.
sn = lu1 + lu2 + ... + lun = lSn ;
lim sn = lim ( lSn ) = l lim Sn = lS .
®¥
n®¥
2) Если nряды
и n®¥
сходятся, то
v
+
v
u1 + u2 + ... + un + ...
1
2 + ... + vn + ...
1) Если ряд
сходится ряд
u1 ± v1 ) + ( u2 ± v2 ) + ... + ( un ± vn ) + ... = S ¢ ± S ¢¢.
(
Доказательство.
sn = ( u1 ± v1 ) + ( u2 ± v2 ) + ... + ( un ± vn ) = Sn¢ ± S n¢¢ ,
lim s = lim ( S ¢ ± S ¢¢ ) = S ¢ ± S ¢¢.
n
n
n и ряд, в котором выброшено
3) Если ряд nсходится,
то
сходится
®¥
n®¥
конечное число членов.

6. Следствие.

Если ряд сходится, то сходится и любой его остаток.

7. 13.1.2. Необходимый признак сходимости ряда. Гармонический ряд.

Необходимый признак. Если ряд сходится, то
n®¥
Доказательство. Sn = u1 + u2
lim un = 0.
lim Sn-1 = S , lim Sn = S ,
n®¥
n®¥
lim un ¹ 0,
n®¥
Если
Пример.
+ ... + un = S n-1 + un ,
lim un = lim ( S n - Sn-1 ) = S - S = 0.
n®¥
n®¥
то ряд расходится.
1
2
n
+
+ ... +
+ ...,
101 201
100n + 1
n
1
lim un = lim
=
¹ 0.
Ряд расходится.
n®¥
n®¥ 100n + 1 100
lim un = 0
Вообще стремление
не означает
n®¥
сходимости ряда.

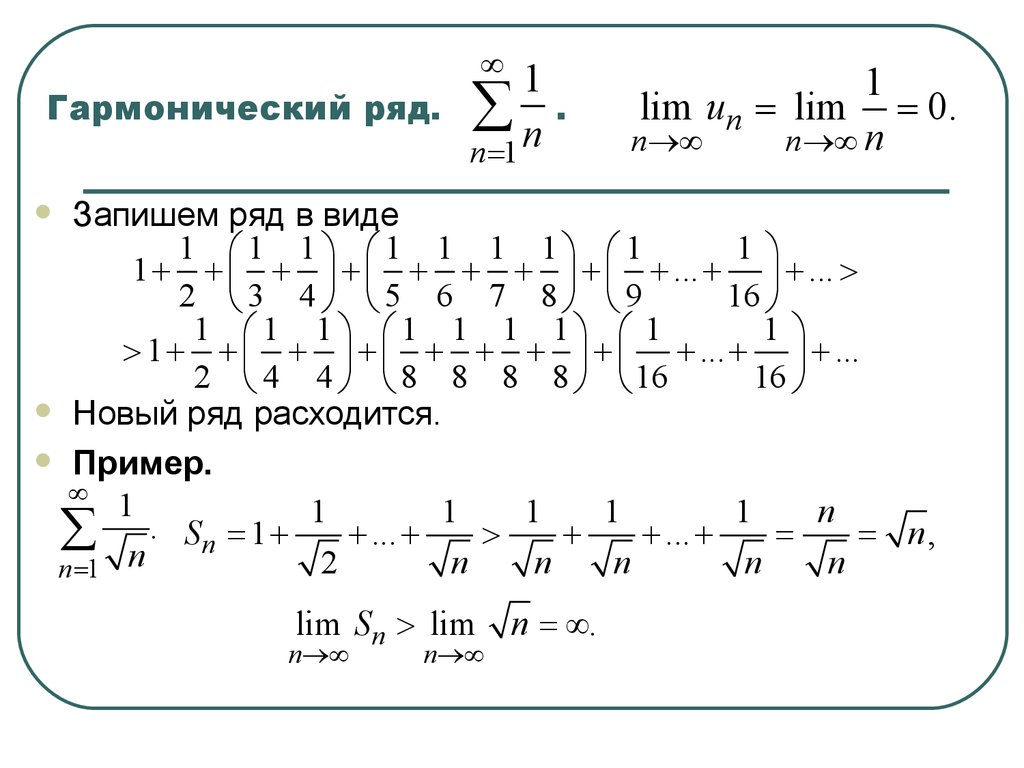
8. Гармонический ряд. .

¥
1
Гармонический ряд. å .
n =1 n
1
lim un = lim = 0.
n®¥
n®¥ n
Запишем ряд в виде
1 æ1 1ö æ1 1 1 1ö æ1
1 ö
1 + + ç + ÷ + ç + + + ÷ + ç + ... + ÷ + ... >
2 è3 4ø è5 6 7 8ø è9
16 ø
1 æ1 1ö æ1 1 1 1ö æ 1
1 ö
> 1 + + ç + ÷ + ç + + + ÷ + ç + ... + ÷ + ...
2 è 4 4 ø è 8 8 8 8 ø è 16
16 ø
Новый ряд расходится.
Пример.
¥
1
1
1
1
1
1
n
.
å n Sn = 1 + + ... + > + + ... + = = n ,
2
n
n
n
n
n
n=1
lim Sn > lim
n®¥
n®¥
n = ¥.

9. 13.1.3. Ряды с положительными членами. Достаточные признаки сходимости ряда. 13.1.3.1. Признаки сравнения.

Рассмотрим ряд u1 + u2 + ... + un + ... такой, что "n un > 0.
Лемма. Если частичные суммы ряда с положительными
членами ограничены сверху S n < M , то ряд сходится.
Доказательство. S1 < S 2 < ... < S n < ..., т.к. un > 0. Если
последовательность монотонно возрастает и ограничена
сверху, то по признаку сходимости Вейерштрасса она
lim Sn = S < M .
имеет предел
n®¥
Если ряд сходится, то S n < S .
Если ряд с положительными членами расходится, то
lim Sn = +¥.
n®¥

10. Признак сравнения.

Пусть
¥ даны два
¥ ряда с положительными членами
å un
n =1
(1),å vn (2), ( un > 0, vи
n > 0)
"n un £ vn . (*)
n =1
Тогда:
1) если сходится ряд (2), то сходится ряд(1);
2) если расходится ряд (1), то
n расходится
n ряд(2).
Sn = å uk , sn = å vk ,
Доказательство. 1)
sn < s Þ Sn £ s n < s.
k =1
k =1
В силу леммы ряд (1) сходится.
2) Sn ® ¥, s n ³ Sn Þ s n ® ¥.
Признак справедлив, если условие (*) выполняется с
какого-либо номера N в силу 3-го свойства сходящихся
рядов.

11. Пример

¥
1
å n.
n =1
Сравним с расходящимся рядом
1
1
"n
³ Þ
n n
¥
1 .
ån
n =1
исходный ряд расходится.

12. Предельный признак сравнения.

un
lim
= A > 0, то ряды (1) и (2) сходятся или
Если
n®¥ vn
расходятся одновременно.
un
"e > 0 $N : "n > N
- A < e или
Доказательство.
u
vn
A - e < n < A + e.
vn
Пусть ряд (2) сходится.
¥ Тогда по свойству 1 сходящихся
рядов сходится ряд å ( A + e ) vn и т.к. un < ( A + e ) vn "n > N
n =1
следовательно ряд (1) сходится. Если ряд (2) расходится,
то в силу un > ( A - e ) vn "n > N
ряд (1) расходится.

13. Пример.

¥
¥
n =1
n =1
2n
å un = å 3n2 - 1.
¥
¥
1
Сравним с расходящимся рядом å vn = å .
n =1
n =1 n
un
2n
2
lim
= lim 2 × n = .
3
n®¥ vn
n®¥ 3n - 1
Исходный ряд расходится.

14. 13.1.3.2. Признак д’Аламбера.

¥
Пусть дан ряд
å u n ( un > 0 ) .
n=1
Если существует предел
un+1
lim
= r,
n®¥ un
то
при r < 1 - ряд сходится,
при r > 1 - ряд расходится,
при r = 1 - ряд может сходится или расходиться.

15. Доказательство.

un+1
Пусть r < 1 Þ $N : "n > N
< r + e = r1, e. > 0
un
r + e = r1 < Тогда
1.
Следовательно
т.е.
u N +1
uN +2
< r1,
< r1 , ... Þ u N +1 < r1u N , u N +2 < r12u N , ...
uN
u N +1
¥
¥
n =1
n =1
å un < u N å
Т.к. последний ряд есть бесконечно
r1n .
убывающая геометрическая прогрессия, то исходный ряд
сходится.
Пусть
и
т.е. ряд расходится.
r > 1 Þ un+1 > un
lim un ¹ 0,
n®¥

16. Примеры.

¥
1)
n
å 2n .
n =1
Применим признак д’Аламбера.
n + 1 2n 1
lim n +1 ×
= < 1.
n 2
n®¥ 2
Ряд сходится.
¥
1
2)
д’Аламбера.
å n2 . Применим признак
n2
n=1
lim
= 1.
2
n®¥ ( n + 1)
О сходимости ряда ничего сказать нельзя. Необходимо
применить другой достаточный признак сходимости.

17. 13.1.3.3. Радикальный признак Коши.

¥
Пусть дан ряд
å un ( un > 0 ) .
n =1
Если существует предел
lim n un = l ,
n®¥
то
при l < 1 - ряд сходится,
при l > 1 - ряд расходится,
при l = 1 - ряд может сходится или расходиться.

18. Пример.

¥
Пример.
å ln n
n =1
1
( n + 1)
.
Применим радикальный признак Коши.
1
1
lim n n
= lim
= 0 < 1.
n®¥ ln ( n + 1)
n®¥ ln ( n + 1)
Ряд сходится.