ЕГЭ. Задачи на смеси и сплавы

2.

ГБОУ СОШ с. Пестравка
Пестравского района Самарской области
ЕГЭ
ЗАДАЧИ
НА СМЕСИ И СПЛАВЫ
золото
серебро
В 13

3.

Способы решения задач
на смеси и сплавы
Арифметический
Применение уравнения
Применение систем уравнений

1
В сосуд, содержащий 5 литров 12 процентного
водного раствора некоторого вещества, добавили
7 литров воды. Сколько процентов составляет
концентрация получившегося раствора?
I способ
12 % 0,6л
5л
+
0%
7л
5 7 12( л)
=
0,6л
12 л
5 0,12 0,6( л)
0,6
100 5%
12
Ответ: 5%
Решение

6.

7.

В сосуд, содержащий 5 литров 12 процентного
водного раствора некоторого вещества, добавили
7 литров воды. Сколько процентов составляет
концентрация получившегося раствора?
III способ
Объем раствора увеличился в 2,4 раза
(было 5 л, стало 12 л 12:5 = 2,4),
содержание вещества не изменилось, поэтому
процентная концентрация получившегося
раствора уменьшилась в 2,4 раза.
12:2,4=5(%)
Ответ: 5%
Решение

8.

Смешали 4 литра 15 процентного водного
2
раствора с 6 литрами 25 процентного водного
раствора этого же вещества. Сколько процентов
составляет концентрация получившегося раствора?
p1V1 p2V2
p
V1 V2
15 4 25 6 210
p
21%
4 6
10
Ответ: 21%
Решение

9.

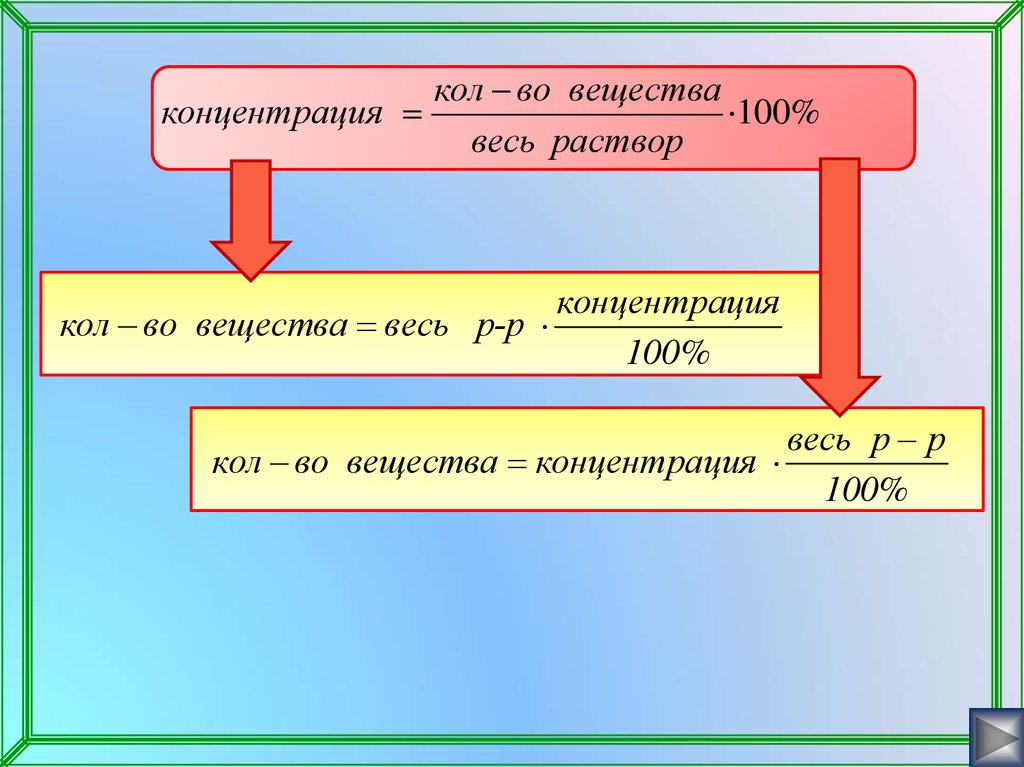
кол во вещества
концентрация
100%
весь раствор
концентрация
кол во вещества весь р-р
100%
весь р р
кол во вещества концентрация
100%

10.

3
15% = 0,15
25% = 0,25
Смешали 4 литра 15-процентного водного раствора
некоторого вещества с 6 литрами 25-процентного водного
раствора этого же вещества. Сколько процентов составляет
концентрация получившегося раствора?
Сколько вещества
было в растворе?
1) 4 · 0,15 = 0,6 (л)
в 1 растворе
кол вещества
во вещества
концентрация
100%
раствор
2) 6 · 0,25 = 1,5 (л)весь
вещества
во 2
растворе Весь
Вещество в
Задачи 21-22
+
+
раствор
растворе
1 р-р
4
0,6
2 р-р
6
1,5
100%
Ответ: 21

11.

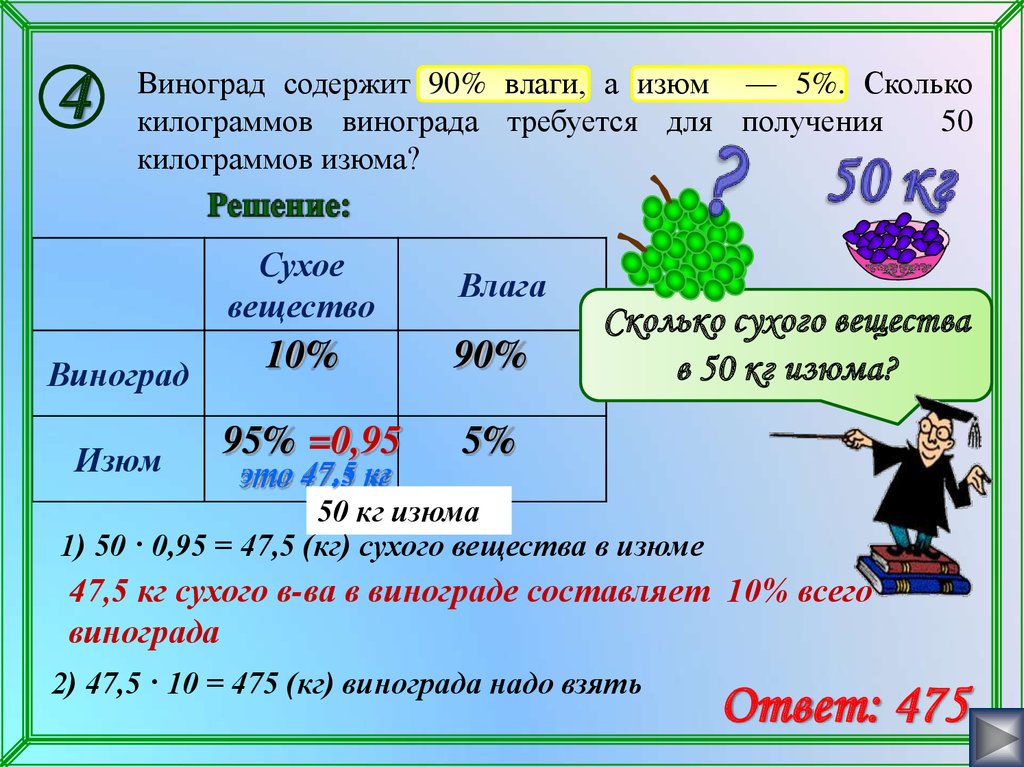
4
Виноград содержит 90% влаги, а изюм — 5%. Сколько
килограммов винограда требуется для получения
50
килограммов изюма?
Сухое
вещество
Влага
Виноград
10%
90%
Изюм
95% =0,95
5%
Сколько сухого вещества
в 50 кг изюма?
это 47,5 кг
50 кг изюма
1) 50 · 0,95 = 47,5 (кг) сухого вещества в изюме
47,5 кг сухого в-ва в винограде составляет 10% всего
винограда
2) 47,5 · 10 = 475 (кг) винограда надо взять
Ответ: 475

12.

Самостоятельная работа.
Собрали 8 кг свежих цветков ромашки,
влажность которых 85%. После того как
цветки высушили, их влажность составила
20%. Чему равна масса цветков ромашки
после сушки?

13.

Решение задач
с помощью уравнений

14.

5
15% = 0,15
21% = 0,21
Смешали некоторое количество 15-процентного раствора
некоторого вещества с таким же количеством 21-процентного
раствора этого вещества. Сколько процентов составляет
концентрация получившегося раствора?
кол во вещества
конц ция
100%
весь раствор
Весь
раствор
15% р-р
21 % р-р
Задачи 19-20
Вещество в
растворе
1 р-р
x
0,15x
2 р-р
x
0,21x
+
+
100%
Ответ: 18

15.

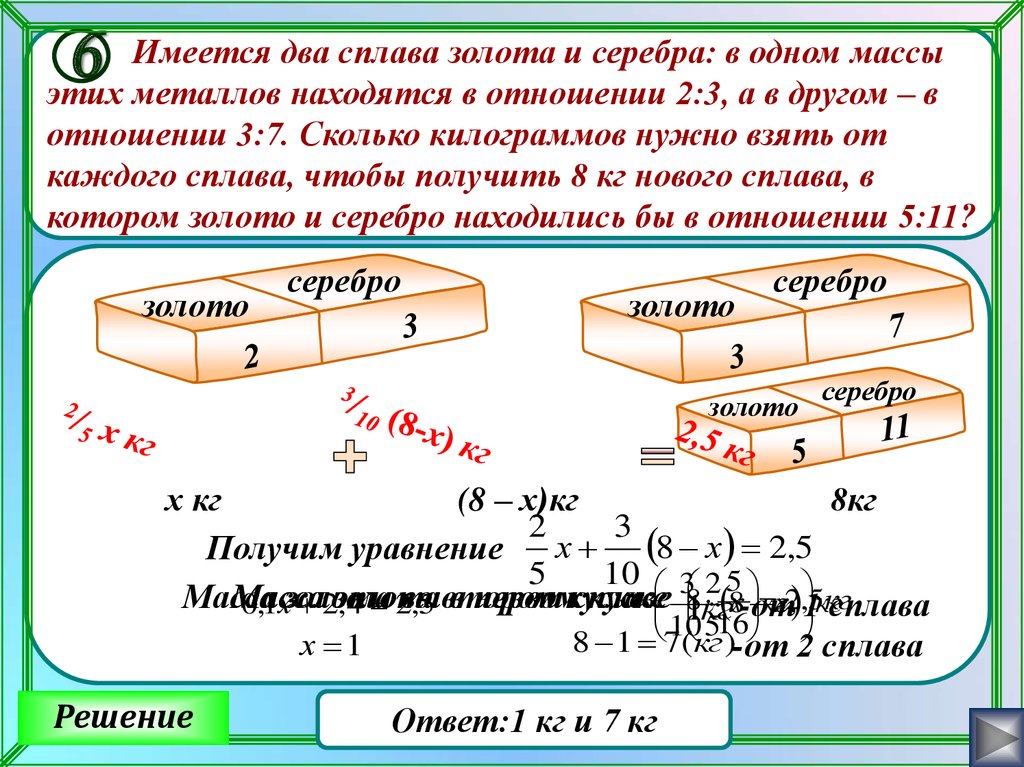
Имеется два сплава золота и серебра: в одном массы
6
этих металлов находятся в отношении 2:3, а в другом – в
отношении 3:7. Сколько килограммов нужно взять от
каждого сплава, чтобы получить 8 кг нового сплава, в
котором золото и серебро находились бы в отношении 5:11?
серебро
серебро
золото
золото
серебро
серебро
золото
золото
золото
серебро
х кг
(8 – х)кг
8кг
2
3
8 х 2,5
х
Получим уравнение
5
10 3 2 5
Масса
Масса
в первом
новом куске
сплаве
куске 1
8
8х-от
кг
кгх2. , 15кг
0,1хзолота
2золота
,4 2во
,5 втором
кг
сплава
16
10
5
8 1 7( кг )-от
х 1
2 сплава
Решение
Ответ:1 кг и 7 кг

16.

Решение задач
с помощью
систем уравнений

17.

Первый раствор содержит 40% кислоты, а второй 7
60% кислоты. Смешав эти растворы и добавив 5 л воды,
получили 20 процентный раствор. Если бы вместо воды
добавили 5 л 80 процентного раствора, то получился бы
70 процентный раствор. Сколько литров 60 процентного
раствора кислоты было первоначально?
80%
60% + 0%
4л
0,6у л
70%
20%
0,7(х+у+5)
0,2(х+у+5) л
л
40% +
=
0,4х 0,6 у 0,2 х у 5 ;
0,4х л
хл
ул
(х+у+5) л 0,4х 0,6 у 4 0,7 х у 5 .
5л
х 0,6 у 0,2 х 0,2 у 1;
0,40,2(х+у+5)
х 1;
0
,
2
х
0
,
4
у
1
;
0,6у
0,7(х+у+5)
(л)
кислоты
(л)
(л)
кислоты
кислоты
во
втором
в
в
новом
новом
растворе
растворе
растворе
кислоты
растворе
0,4х (л) 0-,8
кислоты
в 5 литрах
5 4( л)в первом
0,4 х 0,6 у 4 0,7 х 0,7 у 3,5. 0,3х 0,1у 0,5. у 2.
Решение
Ответ: 2 л

18.

8
Смешав 91-процентный и 93-процентный растворы кислоты
и добавив 10 кг чистой воды, получили 55-процентный
раствор кислоты. Если бы вместо 10 кг воды добавили 10 кг
50-процентного раствора той же кислоты, то получили бы
75-процентный раствор кислоты. Сколько килограммов 91процентного раствора использовали для получения смеси?
Весь
раствор
Вещество в
растворе
1 р-р
x
0,91x
2 р-р
y
0,93y
+
+
+ 10
10 кг
·100% = 55
93 % р-р
55% р-р

19.

Смешав 91-процентный и 93-процентный растворы
50%кислоты
= 0,5 и
добавив 10 кг чистой воды, получили 55-процентный раствор
кислоты. Если бы вместо 10 кг воды добавили 10 кг 50процентного раствора той же кислоты, то получили бы 75процентный раствор кислоты. Сколько килограммов 91процентного раствора использовали для получения смеси?
Весь
раствор
1 р-р
?
x
Искомая
Вещество в
растворе
0,91x
величина
2 р-р
y
0,93y
10 · 0,5 = 5 (кг) кислоты в р-ре
+
+
+ 5· 100 = 75
+ 10

20.

Составим и решим систему уравнений:
0,91х 0,93 у
х у 10 100 55
0,91х 0,93 у 5 100 75
Задачи 25-28
х у 10
(0,91х 0,93 у ) 100 55( х у 10)
(0,91х 0,93 у 5) 100 75( х у 10)
18 х 19 у 275
8 х 9 у 125
Ответ: 10

English Русский Правила