Геология. Строение зон разрывных нарушений в горных породах. (Лекция 9)

1. Строение зон разрывных нарушений

2.

«Разрыв – поверхность или зона в горных породах, по которой
произошло смещение разделяемых этой поверхностью блоков»,
то есть разрывы не всегда имеют вид одной поверхности,
часто они представляют собой зоны различной мощности,
имеющие сложное строение.
Поскольку при смещении блоков друг относительно друга требуется
преодолевать силу трения, в зоне сместителя возникают разнообразные
структурные элементы, связанные с этим процессом:
– зоны дробления (тектонические брекчии);
– зеркала скольжения;
– зоны рассланцевания;
– зоны истирания (милониты).

3. Тектонические брекчии

Крупноглыбовая тектоническая брекчия. Долина
Смерти. Калифорния.
http://www.portervillecollege.edu/…/ Breccia202.JPG
Слабо сцементированная тектоническая
брекчия. В матриксе – лимонитизированная
глина
Тектонические брекчии образуются за
счет разрушения пород,
соприкасающихся по разрыву. Обломки
имеют угловатую форму, обычно они
сцементированы гидротермальными
минералами (кварц, кальцит, лимонит)
Среднеобломочная тектоническая
брекчия. Траппы Норильской
мульды. Фото А.В. Рудаковой

4.

Тектонические брекчии по кварцевым
жилам – очень распространенный вид
тектонических брекчий. Кварцевые
жилы формируются в зонах разрывов,
а последующие движения по этим
разрывам приводят к разрушению
монолитного жильного кварца.
Тектоническая брекчия с лимонитовым цементом.
В обломках – жильный кварц. Ю. Урал
В условиях высокой проницаемости
зон разрывов матрикс часто
замещается различными
гидротермальными минералами, в
том числе, и более поздним кварцем
Тектоническая брекчия с кварцевым цементом.
В обломках – жильный кварц. Ю. Урал

5.

Мелкообломочная тектоническая
брекчия с лимонитизированным
матриксом. Ю. Урал
Тектоническая брекчия с
лимонитовым цементом
по кварцевой жиле. Ю. Урал
При продолжительных деформациях тектонические брекчии могут подвергаться
повторной тектонизации, обломки расплющиваются и разворачиваются,
появляется ориентировка раздавленных обломков, параллельная сместителю.
Тектонические брекчии с кварцевым цементом
и линейной текстурой по кварцитам. Ю. Урал

6.

Зеркала скольжения
Схема формирования
зеркал скольжения. По
Ramsay, Huber, 1983
Зеркала скольжения представляют
собой субпараллельные борозды на поверхности
сместителя.
Они образуются за счет трения между
перемещаемыми блоками пород и трассируют
направление смещения.
По положению зеркала в пространстве и
характеру борозд можно определить тип разлома
и направление смещения по нему.
Определение направления
смещения. По Хоку и
Миллеру, 1993
На поверхности зеркал скольжения
часто присутствуют мелкие
уступчики, поперечные к бороздкам,
и ямки. Они могут образовываться:
1) за счет образования мелких
отрывов, не мешающих
скольжению;
2) за счет формирования мелких
упоров, препятствующих скольжению
и сопровождающихся вследствие
этого мелкими трещинами скола.

7.

8.

Поскольку зеркало скольжения представляет собой поверхность, ее ориентировка
в пространстве определяется элементами залегания – азимутом и углом падения
этой поверхности.
Борозды на поверхности сместителя (штриховка) представляют собой линии,
которые обычно ориентированы косо к поверхности зеркала, а поэтому имеют
свои собственные элементы залегания.
Азимут падения штриховки отличается от азимута падения поверхности зеркала
в пределах ±90 , а угол падения штриховки колеблется от 0 до собственного
угла падения поверхности зеркала.
По положению зеркала в пространстве и характеру борозд можно определить
тип разлома и направление смещения по нему.
Штриховки на зеркале
при сбросе или взбросе
60
при сдвиге
60
при комбинированном
разрыве
60
30

9.

Штриховка на зеркале
при сбросе или взбросе
Зеркало скольжения взброса,
штрихи направлены по падению
наклонного сместителя. Ю. Урал
Зеркало скольжения надвига,
штрихи направлены по падению
пологого сместителя. Ю. Урал

10.

Штриховка на зеркале
при сдвиге
Зеркало скольжения сдвига с вертикальным
сместителем, штрихи на сместителе
горизонтальны. Ю. Урал
Зеркало скольжения сдвига с
вертикальным сместителем,
штрихи на сместителе
горизонтальны. Ю. Урал

11.

Штриховка на
зеркале при сдвиге
Зеркало скольжения пологого сдвига,
штрихи ориентированы горизонтально
на наклонном сместителе. Ю. Урал
Зеркало скольжения горизонтального надвига,
штрихи показывают направление смещения
на горизонтальном сместителе. Ю. Урал

12.

Зеркало скольжения горизонтального надвига,
штрихи показывают направление смещения
на почти горизонтальном сместителе. Ю. Урал
Зеркало скольжения горизонтального надвига,
штрихи показывают направление смещения
на почти горизонтальном сместителе. Ю. Урал

13.

Зеркало скольжения взбросо-сдвига,
штрихи показывают направление
смещения на крутом сместителе. Ю. Урал.
Фото из архива ОАО Челябинскгеосъемка
Штриховка на зеркале при
разрыве комбинированной
кинематики
В названии разрыва в
конце – компонента с
большей амплитудой!
Зеркало скольжения взбросо-сдвига,
штрихи показывают направление
смещения на крутом сместителе. Ю. Урал

14. Зоны рассланцевания

Сланцеватость – плоскостная текстура горных пород, образованная плоско
параллельным расположением пластинчатых или листоватых минералов.
Как правило, сланцеватость параллельна
поверхности сместителя, что позволяет
использовать ее для определения
морфологии разрыва даже в том случае,
когда он непосредственно не наблюдается.
При этом зоны рассланцевания не имеют
резких границ.
Приразломная зона
рассланцевания
алевролитов. Ю. Урал.
Приразломная зона
рассланцевания
известняков. Ю. Урал

15.

Принадвиговые зоны
рассланцевания
метапесчаников. Ю. Урал.
Фрагмент геологической
карты Южного Урала

16. Милониты

Милониты протерозоя по архейским гнейсам
и кристаллическим сланцам. Ю. Урал.
Милониты – агрегаты тонкоперетертых
зерен первичных пород, частично
перекристаллизованных.
Милониты образуются при фрикционном
скольжении между плоскостями, они
могут проникать
в трещины вмещающей породы.
Смятые в складки
милониты по долеритам.
Фото А.Б. Кирмасова

17.

Мигматизированные архейские
гнейсы, пересеченные зоной
милонитов. Ю. Урал.
Керн с глубины 214 м.
Милониты раннего протерозоя
по архейским мигматитам. Ю.
Урал. Керн с глубины 150 м.

18. Модели формирования разрывов

19. Понятие о деформациях

20.

Общая деформация геологических объектов это изменение:
во-первых – местоположения (перемещение, перенос, трансляция);
во-вторых – ориентировки (вращение);
в-третьих – объема и формы:
дилатация – изменение объема при сохранении формы
дисторсия – искажение формы
Вращение
Перемещение
Дилатация
Дисторсия
Строго говоря,перемещение
и вращение– не деформации
Простейшие примеры:
перемещения – смещения блоков по разрывам;
вращения – поворот крыльев складки при изгибе;
дилатации – уплотнение нелитифицированных осадков;
дисторсии – раздавливание, складчатость, рассланцевание, будинаж и пр.
Общая деформация геологических объектов происходит в результате
приложения самых разных сил, что чаще всего приводит к изменению и
формы, и положения объектов.

21. Меры деформаций

Для описания количественных характеристик деформаций различают три их типа:
линейная
– изменение формы в одном направлении;
плоская
– изменение формы в двух направлениях;
объемная
– изменение формы в трех направлениях.
Линейная деформация
Реальные деформации тел
практически всегда объемны, а
линейные и плоские деформации
являются лишь удобными
моделями!
L0 – начальная длина очень тонкого стержня, толщиной которого
можно пренебречь;
L1 – конечная длина очень тонкого стержня;
L – абсолютное удлинение
L
Меры линейной деформации:
– относительное удлинение (L1 – L0) / L0 L / L0
– растяжение
S L1 / L0 (1 + )
1
L0
2
L1

22.

Плоская деформация
Общая ситуация заключается в том, линейной деформации в чистом виде в
природе не существует, при растяжении физического тела в одном направлении,
оно неизбежно сжимается в другом. И наоборот, при сжатии в одном
направлении, оно растягивается в другом. Поэтому гораздо удобнее
рассматривать особенности деформации тел в плоскости, которую легко
представить как сечение тела.
Плоские деформации принято делить на однородные и неоднородные.
Бóльшая часть деформаций в природе относится к неоднородным, которые очень
разнообразны. Однородной называется деформация, при которой все
материальные прямые линии, отмеченные в объекте до деформации, остаются
прямыми и после деформации. К однородным деформациям относятся:
1 – чистый сдвиг (удлинение – укорочение); 2 – простой сдвиг (скашивание).
Для упрощения интерпретации характера деформаций часто принимается
допущение об однородности деформаций во всем объеме геологического тела.
"Чистый сдвиг" и "простой сдвиг" не являются "сдвигами"
в геологическом смысле слова! Это только обстановки деформаций.

23. Чистый сдвиг

Чистый сдвиг (удлинение –
укорочение) есть деформация под
действием нормальных напряжений.
Мерами деформации могут служить
два коэффициента:
– продольное относительное удлинение
пр = (L1 – L0) / L0 = L / L0
– поперечное относительное удлинение
поп = (W1 – W0) / W0 = W / W0
W1
W0
L
L1
L0
2
1
W
При деформации чистого сдвига равны
площади прямоугольников 1 и 2, а также
скорости смещения точек на их сторонах.
Деформация
положительна при растяжении
и отрицательна при сжатии!

24. Простой сдвиг

Простой сдвиг (скол) есть деформация
под действием тангенциальных
(касательных) напряжений.
Мерами деформации служат:
– угол , на который отклоняется при сдвиге
сторона мысленного квадрата
– tg .
При деформации простого сдвига площадь
первичного прямоугольника равна площади
полученного параллелограмма.
Скорости смещения точек на скосах изменяются
от нулевой до максимальной, из-за чего
возникает градиент скоростей.
В природе оба типа однородных деформаций
часто встречаются в сочетании.

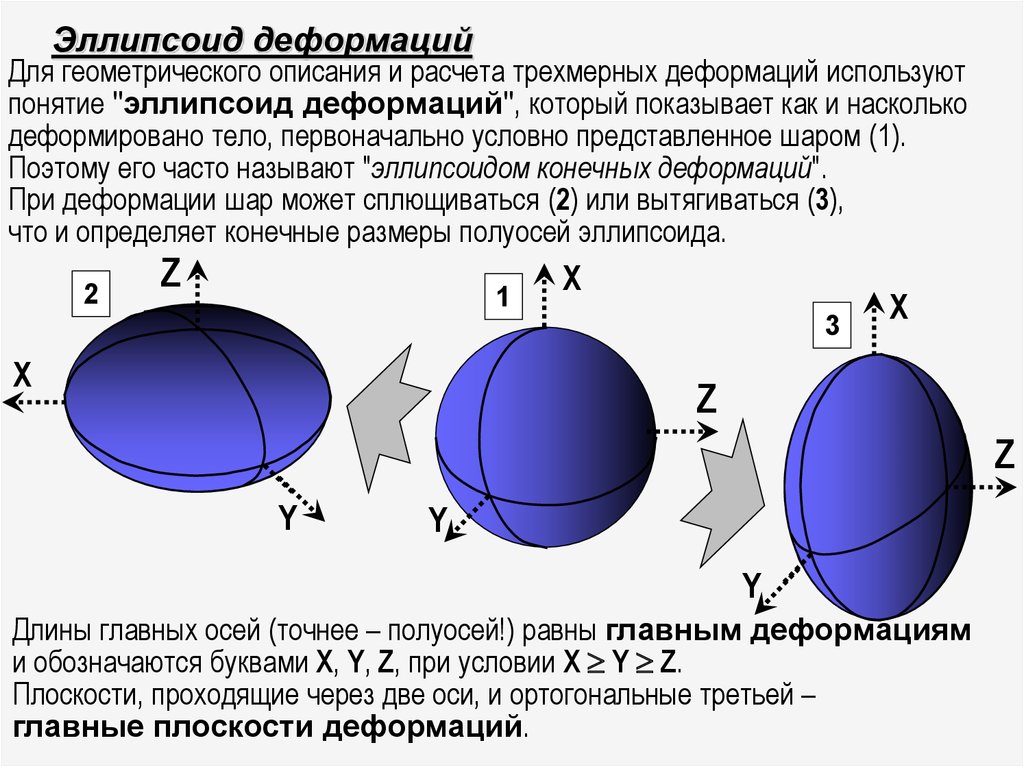
25. Эллипсоид деформаций

Для геометрического описания и расчета трехмерных деформаций используют
понятие "эллипсоид деформаций", который показывает как и насколько
деформировано тело, первоначально условно представленное шаром (1).
Поэтому его часто называют "эллипсоидом конечных деформаций".
При деформации шар может сплющиваться (2) или вытягиваться (3),
что и определяет конечные размеры полуосей эллипсоида.
2
Z
1
X
3
X
X
Z
Z
Y
Y
Y
Длины главных осей (точнее – полуосей!) равны главным деформациям
и обозначаются буквами X, Y, Z, при условии X Y Z.
Плоскости, проходящие через две оси, и ортогональные третьей –
главные плоскости деформаций.

26.

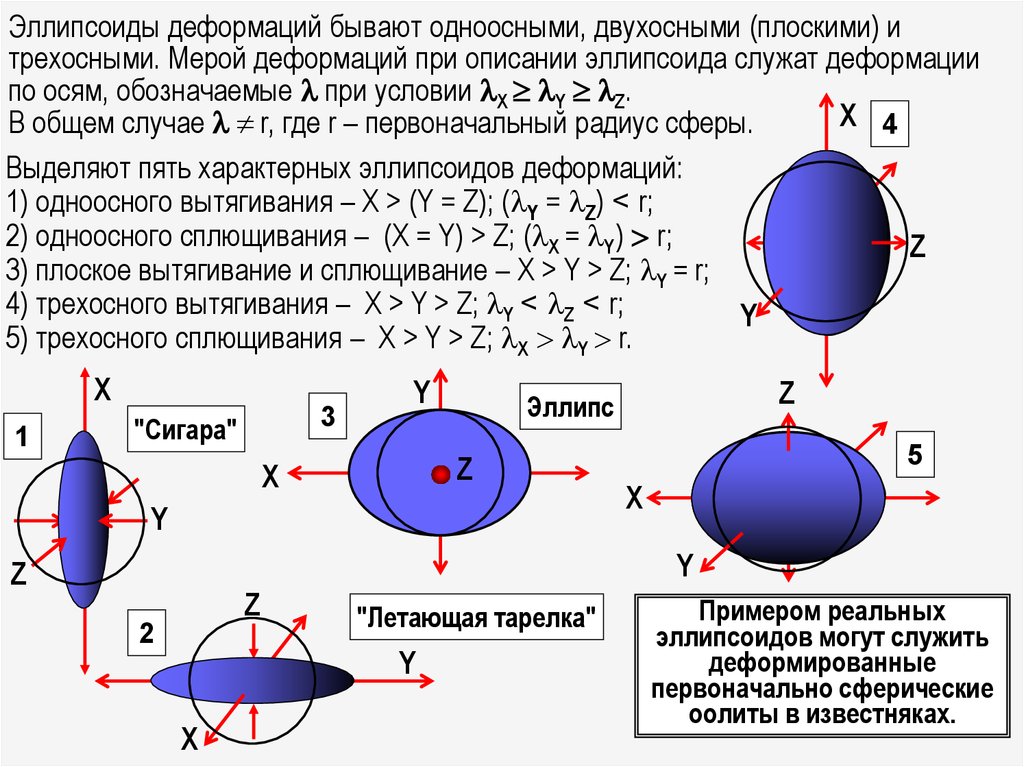
Эллипсоиды деформаций бывают одноосными, двухосными (плоскими) и
трехосными. Мерой деформаций при описании эллипсоида служат деформации
по осям, обозначаемые при условии X Y Z.
X 4
В общем случае r, где r – первоначальный радиус сферы.
Выделяют пять характерных эллипсоидов деформаций:
1) одноосного вытягивания – X > (Y = Z); ( Y = Z) < r;
2) одноосного сплющивания – (X = Y) > Z; ( X = Y) r;
Z
3) плоское вытягивание и сплющивание – X > Y > Z; Y = r;
4) трехосного вытягивания – X > Y > Z; Y < Z < r;
Y
5) трехосного сплющивания – X > Y > Z; X Y r.
X
1
3
"Сигара"
Y
Z
X
Z
Эллипс
Y
5
X
Y
Z
Z
2
"Летающая тарелка"
Y
X
Примером реальных
эллипсоидов могут служить
деформированные
первоначально сферические
оолиты в известняках.

27. Понятие о напряжениях

28.

"Напряжения – это внутренние силы, возникающие в твердом теле под
действием приложенных к нему внешних сил или за счет действия других
факторов, приводящих к деформации этого тела" (А.Б. Кирмасов, 2011).
Сила – величина векторная, т.е. имеет две характеристики:
1 – скалярное значение; 2 – направление приложения.
Напряжение (по идее Коши)
определяется как сила, приложенная к
единице площади – равнодействующая
(F S)
всех сил делится на площадь, к которой
они приложены.
Сила приложена к конкретной площадке, однако
она вызывает трехмерные напряжения и деформации,
которые при неоднородном строении геологических тел
Огюстен Луи Коши
(1789-1857)
очень сложно описывать, а тем более – рассчитывать.
Для «небольших» геологических тел обычно принимается допущение об
«однородности напряжений», т.е. о том, что величина и направление напряжений
равны во всех точках тела. Это допущение далеко не всегда приемлемо для
крупных структур. Поэтому для анализа распределения напряжений используют
бесконечно малый виртуальный куб породы, считая, что уж внутри-то этого
маленького куба напряжение точно однородно. Напряжение рассчитывают для
грани этого куба (для бесконечно малой площадки).

29.

Виртуальный элементарный куб мысленно располагают в определенной
системе координат. Очень удобно рассматривать напряжения
относительно граней этого куба.
Действующая на тело (на площадку) сила (F) вызывает напряжение,
которое по правилу параллелограмма можно разложить
на этой площадке на две составляющие:
– нормальное ( )
напряжение перпендикулярно
x
поверхности (грани куба)
– тангенциальное ( ), или
y
касательное напряжение выражено
на поверхности (или на площадке).
Тангенциальное напряжение в свою
очередь тоже может быть разложено
на составляющие x и y
соответственно осям х и у
виртуального куба.
Напряжения уравновешивают тело:
оно не движется ( уравновешивает
нормальную составляющую силы)
и не вращается ( уравновешивает
тангенциальную составляющую силы)
z
y
F
x

30.

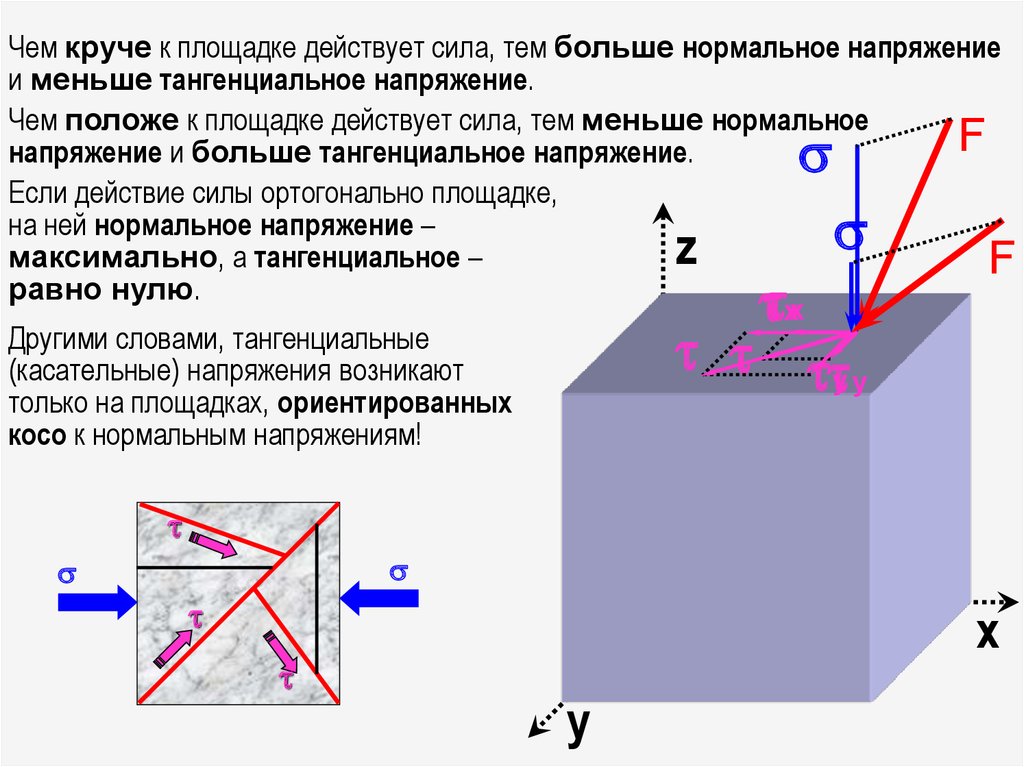
Чем круче к площадке действует сила, тем больше нормальное напряжение
и меньше тангенциальное напряжение.
Чем положе к площадке действует сила, тем меньше нормальное
F
напряжение и больше тангенциальное напряжение.
Если действие силы ортогонально площадке,
на ней нормальное напряжение –
максимально, а тангенциальное –
F
равно нулю.
z
xx
y y
Другими словами, тангенциальные
(касательные) напряжения возникают
только на площадках, ориентированных
косо к нормальным напряжениям!
x
y

31.

Мы не в силах менять направление сил,
но мы можем выбрать любую систему
координат относительно направления
приложения силы. В том числе и такую, в
которой на всех трех взаимно
перпендикулярных плоскостях
тангенциальные напряжения обращаются
в нуль.
В этом случае поле напряжений
можно будет описать только
нормальными напряжениями.
Такие напряжения называют главными
нормальными напряжениями.
Главные нормальные напряжения
обозначают буквами
1, 2 и 3, где
1 – максимальное,
2 – среднее,
3 – минимальное.
z
3
x
1
1– 2
y
2
3
Разница между максимальным и
минимальным напряжениями называется
дифференциальным напряжением.
Направления действия главных напряжений называются главными
направлениями напряжения, а плоскости, проходящие через две оси,
и ортогональные третьей – главными плоскостями напряжений.
1

32.

•Условия, при которых 1 = 2 = 3, называются
литостатическими.
Такие условия возникают при погружении тела на
глубину.
Литостатическое давление просто равно
весу колонны вышележащих пород.
Геологическое тело в
литостатических условиях находится
под равномерными всесторонними и
одинаковыми напряжениями, а
поэтому оно (в простом случае!)
не деформируется.
В литостатических условиях
тангенциальные напряжения
не возникают!
z
3
1
y
1
x
2
3
Среднее нормальное напряжение в литостатических условиях:
ср = ( 1 + 2 + 3) / 3 = 3 1 / 3 = 1

33.

Если главные напряжения не равны друг другу, но литостатическая компонента
присутствует, то ее принято вычитать. Остаток от вычитания называют
девиаторным напряжением
z
1д = ( 1 – л)
2д = ( 2 – л)
3д = ( 3 – л)
В тех случаях, когда, условия не
вполне отвечают литостатическим,
за литостатическую компоненту
принимают усредненное значение
напряжений. Поэтому девиаторные
напряжения можно определить и
через среднее арифметическое:
= ( 1+ 2 + 3)/3
1д = ( 1 – )
2д = ( 2 – )
3д = ( 3 – )
л
3д
л
1д
1
1д
2
л
y
3
3
2д
л
3д
1
x
л

34.

В приповерхностных условиях (при малом литостатическом давлении) одни
напряжения будут растягивающими, а другие – сжимающими,
т.е. будут иметь разные знаки.
В глубине Земли все напряжения будут сжимающими, т.е. будут иметь
одинаковый знак, но при условии их неравенства, одни из них окажутся
относительно растягивающими,
а другие – относительно сжимающими.
В отечественной литературе приняты
3
следующие буквенные обозначения
напряжений:
1 – растягивающее,
2 – среднее,
3 – сжимающее.
z
1
В западной литературе
приняты обратные
обозначения напряжений:
1 – сжимающее
3 – растягивающее!
x
2
y
1
3

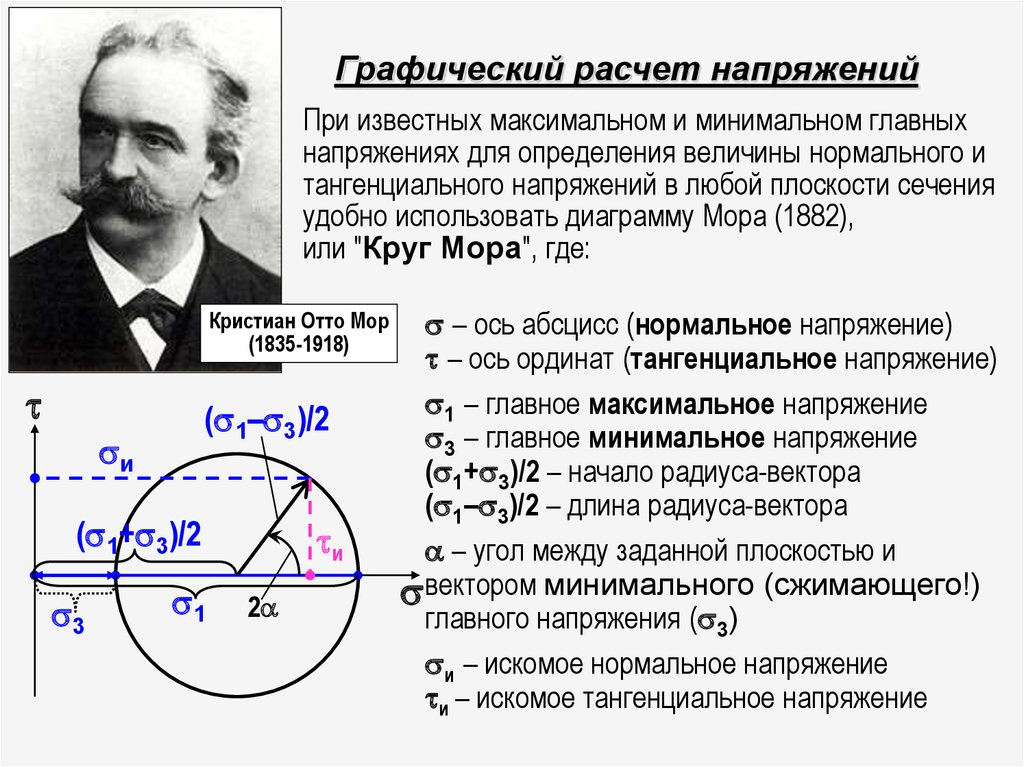
35. Графический расчет напряжений

При известных максимальном и минимальном главных
напряжениях для определения величины нормального и
тангенциального напряжений в любой плоскости сечения
удобно использовать диаграмму Мора (1882),
или "Круг Мора", где:
Кристиан Отто Мор
(1835-1918)
( 1– 3)/2
и
( 1+ 3)/2
3
1
и
2
– ось абсцисс (нормальное напряжение)
– ось ординат (тангенциальное напряжение)
1 – главное максимальное напряжение
3 – главное минимальное напряжение
( 1+ 3)/2 – начало радиуса-вектора
( 1– 3)/2 – длина радиуса-вектора
– угол между заданной плоскостью и
вектором минимального (сжимающего!)
главного напряжения ( 3)
и – искомое нормальное напряжение
и – искомое тангенциальное напряжение

36.

и
3
3
и
Величина тангенциального напряжения плавно меняется
по мере изменения угла между вектором главного
сжимающего напряжения и искомой плоскостью
1
1
2
3
Максимальные
тангенциальные
2 3
1
напряжения возникают на площадках,
? под 45
1 1
1 ориентированных
1
1
Как
изобразить
круг
Мора
к
нормальным
напряжениям!
Крайние случаи:
при
условии
1 = 3
Больше
половины
дифференциального они не бывают!
3
3
3
3
1
max
3
1) если = 90 (2 = 180 ), то и = 3, а и = 0;
2) если = 2 = 0 , то и = 1, а и = 0;
3) если = 45 (2 = 90 ), то и = ( 1+ 3)/2, а и = ( 1– 3)/2 (max!)

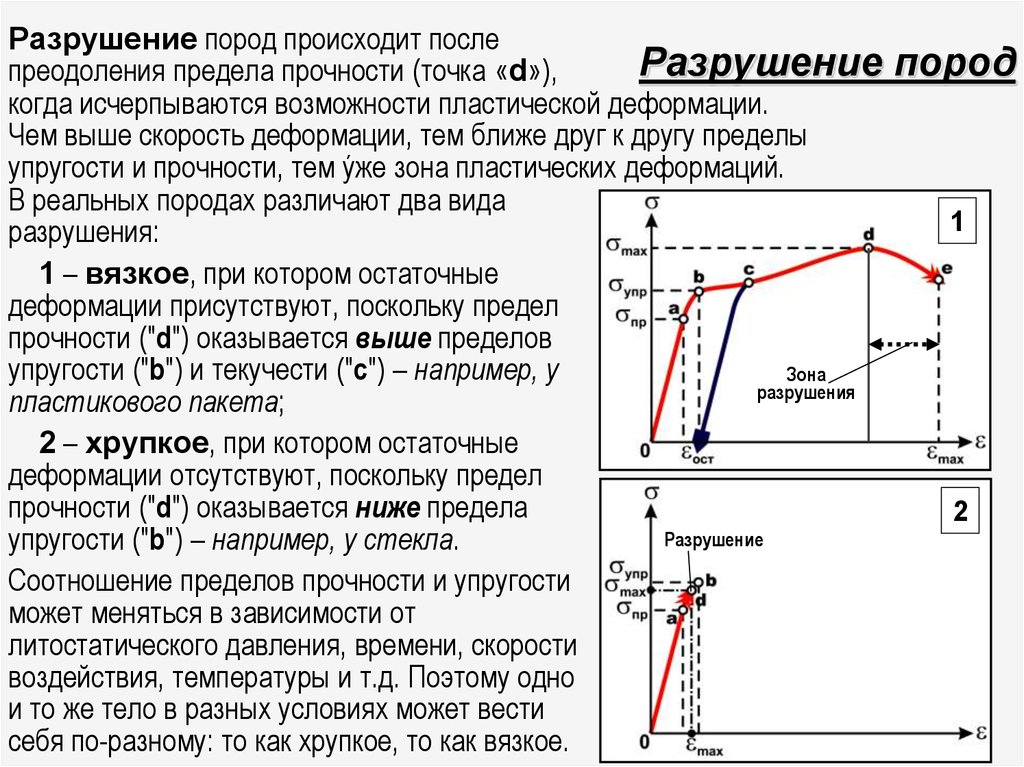
37. Разрушение пород

происходит после
Разрушение
преодоления предела прочности (точка «d»),
когда исчерпываются возможности пластической деформации.
Чем выше скорость деформации, тем ближе друг к другу пределы
упругости и прочности, тем ýже зона пластических деформаций.
В реальных породах различают два вида
разрушения:
1 – вязкое, при котором остаточные
деформации присутствуют, поскольку предел
прочности ("d") оказывается выше пределов
упругости ("b") и текучести ("с") – например, у
Зона
разрушения
пластикового пакета;
2 – хрупкое, при котором остаточные
деформации отсутствуют, поскольку предел
прочности ("d") оказывается ниже предела
Разрушение
упругости ("b") – например, у стекла.
Соотношение пределов прочности и упругости
может меняться в зависимости от
литостатического давления, времени, скорости
воздействия, температуры и т.д. Поэтому одно
и то же тело в разных условиях может вести
себя по-разному: то как хрупкое, то как вязкое.
пород
1
2

38.

Разрушение пород происходит путем образования трещин скалывания и
отрыва, поэтому принято различать пределы прочности пород на отрыв – под
действием нормальных растягивающих напряжений (1) и на скалывание
– под действием касательных напряжений (2), которые для одной и той же
породы могут различаться в зависимости от условий разрушения.
1
3
1
Разрушение образца
гранита в эксперименте
(по Г.Д. Ажгирею, 1956)
1
3
2
1
Разрушение керна
мрамора в эксперименте
(по Э.У. Спенсеру, 1981)
3
3
3
1
1
1
3
Экспериментально показано, что при раздавливании хрупкого образца в прессе
образуются либо трещины отрыва (1), параллельные приложенным силам, либо
трещины скалывания (2), косые по отношению к приложенным силам. При этом
образец укорачивается по направлению сжатия ( 3) и удлиняется по направлению
растяжения ( 1). Первые возникают при низком общем давлении и низком
коэффициенте трения на площадке приложения силы, а вторые – при большом
общем давлении и высоком трении на площадке приложения силы.

39. Прочность пород, угол внутреннего трения

Прочность пород есть свойство сопротивляться воздействию внешних нагрузок
без разрушения. Для того, чтобы разрушить породу необходимо преодолеть вопервых, силу сцепления между зернами и, во-вторых, силу трения между ними.
Прочность породы увеличивается с увеличением всестороннего давления.
Уравнение теории прочности Кулона-Мора: n = n tg + c
где n и n касательное и нормальное напряжения; с – коэффициент сцепления
(зависит от силы связи между зернами); – угол внутреннего трения материала
(зависит от силы трения между зернами при сдвиговой деформации – для горных
пород 35-40 ). tg – называют коэффициентом пропорциональности между
максимальными касательными и нормальными напряжениями.
Для графического определения коэффициента сцепления и угла внутреннего
трения применяют круги Мора для напряжений, разрушающих породу
("предельные круги Мора").
Упрощенная схема результатов
испытаний пород на разрушение
С
"Угол внутреннего трения – показатель прочности горной породы, равный
углу наклона касательной к огибающей предельных кругов напряжений в
точке ее пересечения с осью касательных напряжений" (ГОСТ 30416-96)

40.

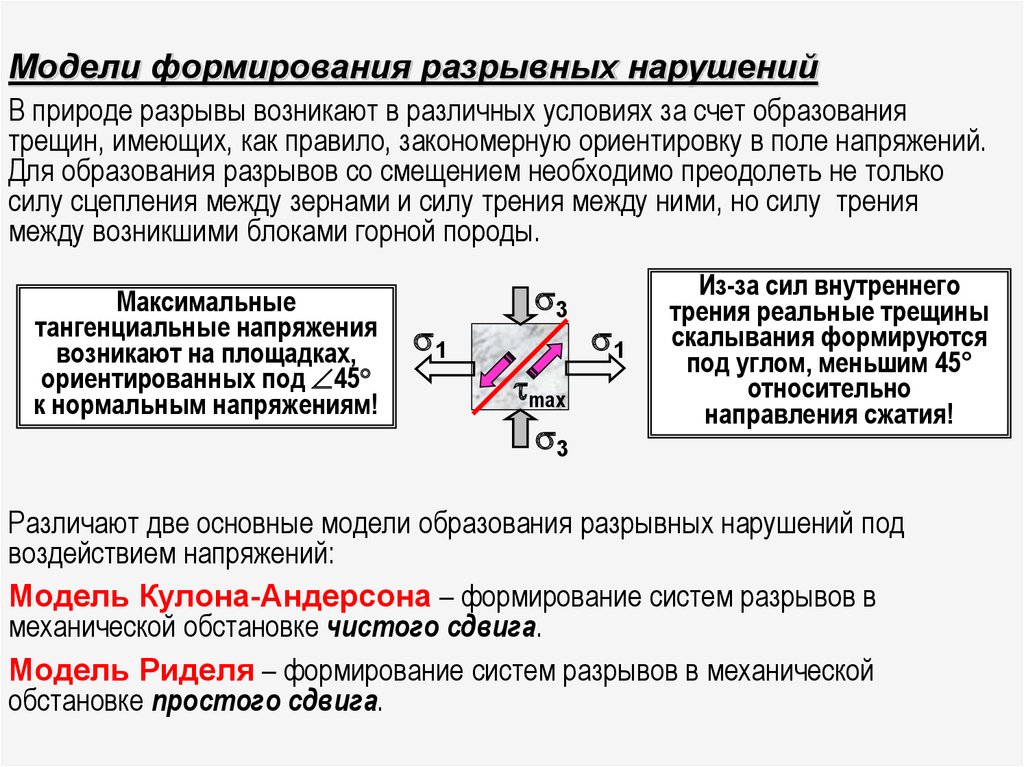
Модели формирования разрывных нарушений
В природе разрывы возникают в различных условиях за счет образования
трещин, имеющих, как правило, закономерную ориентировку в поле напряжений.
Для образования разрывов со смещением необходимо преодолеть не только
силу сцепления между зернами и силу трения между ними, но силу трения
между возникшими блоками горной породы.
Максимальные
тангенциальные напряжения
возникают на площадках,
ориентированных под 45
к нормальным напряжениям!
1
3
max
3
1
Из-за сил внутреннего
трения реальные трещины
скалывания формируются
под углом, меньшим 45°
относительно
направления сжатия!
Различают две основные модели образования разрывных нарушений под
воздействием напряжений:
Модель Кулона-Андерсона – формирование систем разрывов в
механической обстановке чистого сдвига.
Модель Риделя – формирование систем разрывов в механической
обстановке простого сдвига.

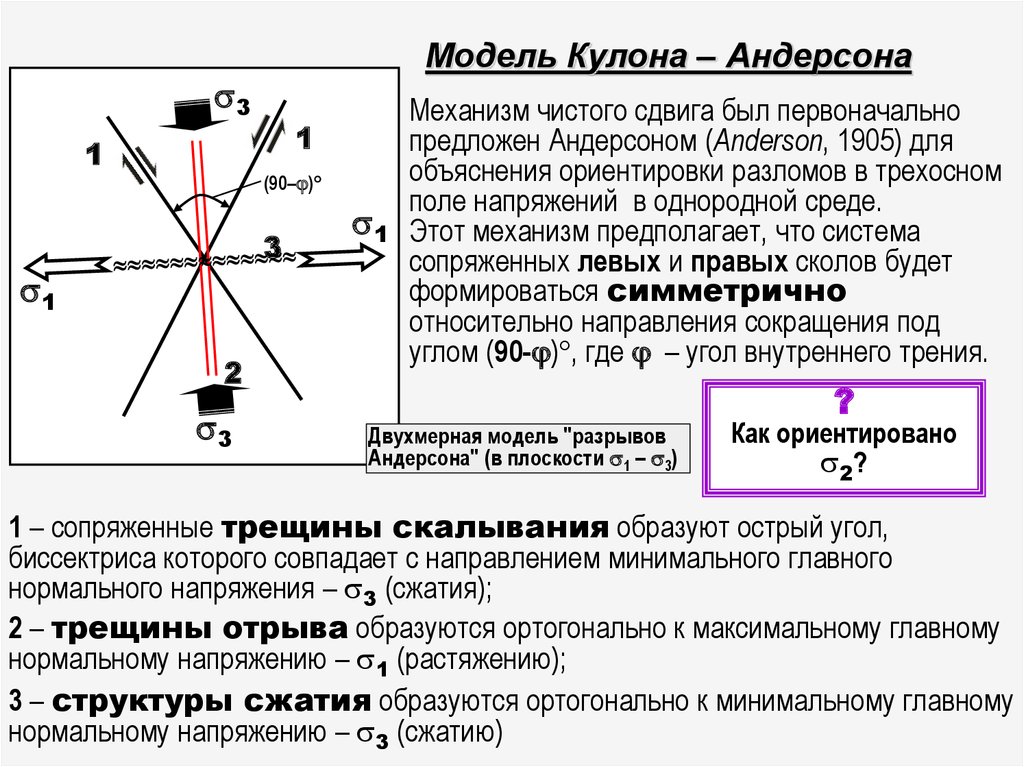
41. Модель Кулона – Андерсона

3
1
1
(90– )
3
1
2
3
1
Механизм чистого сдвига был первоначально
предложен Андерсоном (Anderson, 1905) для
объяснения ориентировки разломов в трехосном
поле напряжений в однородной среде.
Этот механизм предполагает, что система
сопряженных левых и правых сколов будет
формироваться симметрично
относительно направления сокращения под
углом (90- ) , где – угол внутреннего трения.
?
Двухмерная модель "разрывов
Андерсона" (в плоскости 1 – 3)
Как ориентировано
2?
1 – сопряженные трещины скалывания образуют острый угол,
биссектриса которого совпадает с направлением минимального главного
нормального напряжения – 3 (сжатия);
2 – трещины отрыва образуются ортогонально к максимальному главному
нормальному напряжению – 1 (растяжению);
3 – структуры сжатия образуются ортогонально к минимальному главному
нормальному напряжению – 3 (сжатию)

42.

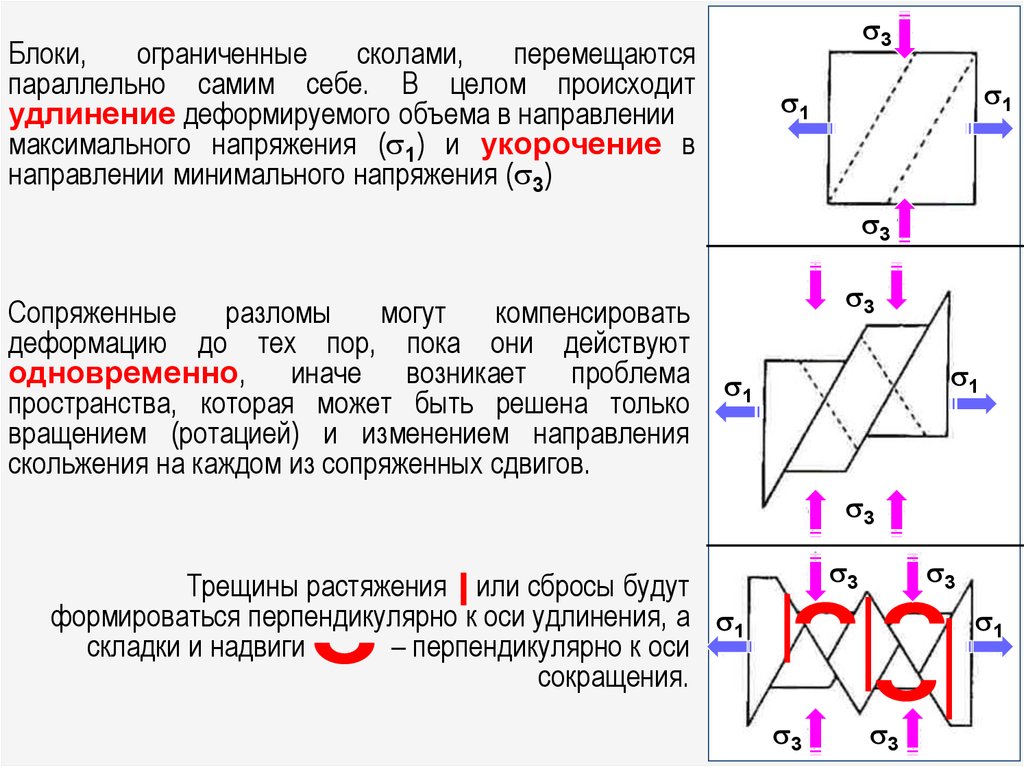
3
Блоки,
ограниченные
сколами,
перемещаются
параллельно самим себе. В целом происходит
удлинение деформируемого объема в направлении
максимального напряжения ( 1) и укорочение в
направлении минимального напряжения ( 3)
1
1
3
Сопряженные
разломы
могут
компенсировать
деформацию до тех пор, пока они действуют
одновременно, иначе возникает проблема
пространства, которая может быть решена только
вращением (ротацией) и изменением направления
скольжения на каждом из сопряженных сдвигов.
3
1
1
3
3
Трещины растяжения или сбросы будут
формироваться перпендикулярно к оси удлинения, а 1
складки и надвиги
– перпендикулярно к оси
сокращения.
3
1
3
3

43.

3
1
2
>90
<90
Таким образом, в модели Андерсона
сдвиги и отрывы всегда строго
ориентированы относительно главных
нормальных напряжений и не меняют
своей ориентировки при развитии
дислокаций
1
1 – отрывы
образуются ортогонально
к направлению растяжения –
максимальному главному нормальному
напряжению ( 1) и лежат в главной
плоскости напряжений 2 – 3
Трёхмерная модель
"разрывов Андерсона"
2 – сопряженные левые и правые сколы образуют:
а) острый плоский угол, биссектриса которого совпадает
с направлением минимального главного нормального
напряжения – сжатия ( 3) и лежит в главной плоскости
напряжений 2– 3,
б) тупой плоский угол, биссектриса которого совпадает
с направлением максимального главного нормального
напряжения – растяжения ( 1) и лежит в главной
плоскости напряжений 2– 1;
Линии пересечения
сколов совпадают
направлением
среднего главного
нормального
напряжения 2!

44. Механизмы сдвигания при чистом сдвиге

Разрывы на геологических картах имеют
конечные размеры. Это не только и даже не
столько результат рисовки карты, сколько
отражение действительности – разрывы на
самом деле имеют конечную длину,
т.е. на концах этих разрывов никакого
смещения нет, а в середине – есть!
Фрагмент Государственной
геологической карты
Южного Урала
Сдвиги Андерсона являются сколами.
Согласно механизму, разработанному самим
Андерсоном, они имеют конечную длину, а
поэтому вдоль всей трассы андерсоновского
сдвига в его крыльях формируются пары
структур: растяжения и сжатия.
Механизм сдвигания
по Андерсону – Риду
(Reid, 1910)

45.

Сжатие
с
Амплитуды смещений
0
Локальные деформации
Растяжение
растяжение
сжатие
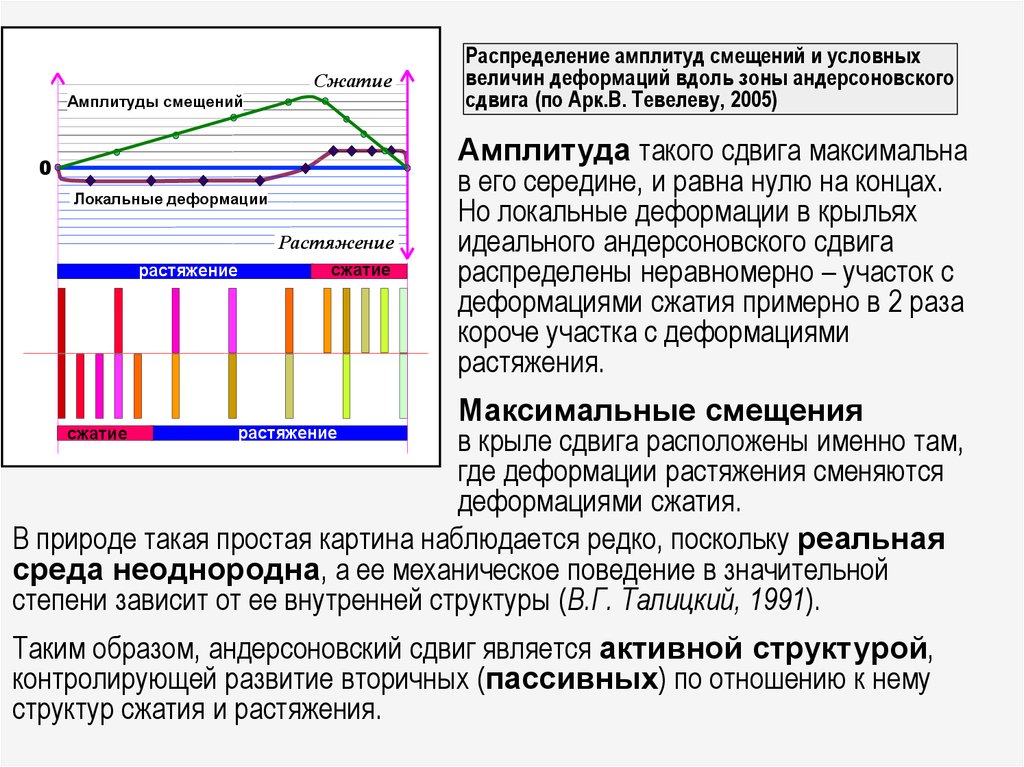
Распределение амплитуд смещений и условных
величин деформаций вдоль зоны андерсоновского
сдвига (по Арк.В. Тевелеву, 2005)
Амплитуда такого сдвига максимальна
в его середине, и равна нулю на концах.
Но локальные деформации в крыльях
идеального андерсоновского сдвига
распределены неравномерно – участок с
деформациями сжатия примерно в 2 раза
короче участка с деформациями
растяжения.
Максимальные смещения
в крыле сдвига расположены именно там,
где деформации растяжения сменяются
деформациями сжатия.
В природе такая простая картина наблюдается редко, поскольку реальная
среда неоднородна, а ее механическое поведение в значительной
степени зависит от ее внутренней структуры (В.Г. Талицкий, 1991).
сжатие
растяжение
Таким образом, андерсоновский сдвиг является активной структурой,
контролирующей развитие вторичных (пассивных) по отношению к нему
структур сжатия и растяжения.

46.

А
Б
А
0
max
А
Как выглядит
разрыв в разрезе?
СБРОС
Б
0
А
?
Б
Б
СДВИГ
СДВИГОСБРОС

47. Модель Риделя

3
Механизм простого сдвига был первоначально
Y R
предложен В. Риделем (Riedel, 1929) для
объяснения ориентировки разломов в
T
однородной среде при преобладании
P
45
тангенциальных напряжений.
В таких условиях возникают серии сколов:
1
синтетических (совпадающих по
1
направлению смещения с главным сдвигом) и
антитетических (с противоположным
90 – 2
смещением) сдвигов.
Y – разломы, параллельные направлению
2
максимальных тангенциальных напряжений
— угол
2
3
внутреннего
(Y-сколы, или генеральные
трения
сдвиги). В данном случае – правые!
R – R-сколы, или сколы Риделя (синтетические сдвиги под + / 2 к
направлению генерального сдвига). В данном случае – тоже правые!
P – Р-сколы, или вторичные сколы Риделя (синтетические сдвиги под - / 2
к направлению генерального сдвига). В данном случае – тоже правые!
R’ – сопряженные сколы Риделя – "антириделевские" (антитетические
сдвиги). В данном случае – левые!
T – трещины отрыва ( ≈ 45° к генеральному сдвигу). Образуются ортогонально
к напряжению растяжения и вдоль напряжения сжатия.

48.

В лабораторных экспериментах
обычно моделируется жесткий
фундамент, включающий разлом
(например из двух жестких досок),
перекрытый покровом осадочных
пород (обычно это слой глины).
Первыми структурами в
перекрывающей глине оказываются
эшелонированные сколы Риделя,
причем их кулисное расположение
прямо зависит от направления
сдвигания в подстилающих досках –
они образуют левокулисное
перекрытие при правом сдвиге
и правокулисный ряд
при левом сдвиге.
В.Г. Талицкий, 1991 (цитируется
по Арк.В. Тевелеву, 2005)
10 см

49.

Направление сдвигания вдоль
сколов R, P, Y то же самое,
что и в разломе фундамента,
а по R’ — противоположное.
Все разломы, исключая надвиги,
близки к вертикальным.
Сколы R и R’ составляют с основной
зоной смещения углы ( 2)° и
(90 – 2)° соответственно,
где – угол внутреннего трения.
Это означает, что риделевские
сколы ориентированы под углом
от 15° до 20° к генеральному сдвигу,
а R’ — под углом от 60° до 75°.
При развитии системы риделевских
сколов возникают сложно
построенные сдвиговые зоны,
составленные из разномасштабных
линзовидных блоков.
В.Г. Талицкий, 1991 (цитируется
по Арк.В. Тевелеву, 2005)
10 см

50.

Набор структур, сформированных
при правом простом сдвиге:
1 – риделевские сколы
(кулисы левосторонние);
2 – складки кулисные
(ориентированы нормально к оси
сжатия, кулисы правосторонние);
3 – сбросы, грабены
(ориентированы нормально к оси
растяжения);
4 – надвиги, взбросы
(ориентированы нормально к оси
сжатия);
5 – сочетание различных
структурных элементов.
Таким образом, в условиях
простого сдвига может
формироваться серия сопряженных
структур сжатия и растяжения.
По Sylvester, 1988 (упрощено,
по Арк.В. Тевелеву, 2000)
1
2
3
4
5
Риделевские
сколы
Складки
кулисные
Сбросы,
грабены
Надвиги,
взбросы
Наложение
разных
структур

51.

Примеры структур, сформированных в обстановке
простого сдвига (модель Риделя)
Зоны
рассланцевания
(Y-сколы)
Дайка аплитов (М=20 см) в габброидах
с трещинами отрыва и Y-сколами на
правом сдвиге. Южный Урал
Трещины
отрыва
(T-трещины)
R
T
T
R
R
T
Правокулисные трещины отрыва и сколы
Риделя на левом сдвиге, выполненные
кальцитом. Ширина зоны 1 см. Известняки
нижнего карбона. Южный Урал
T
R

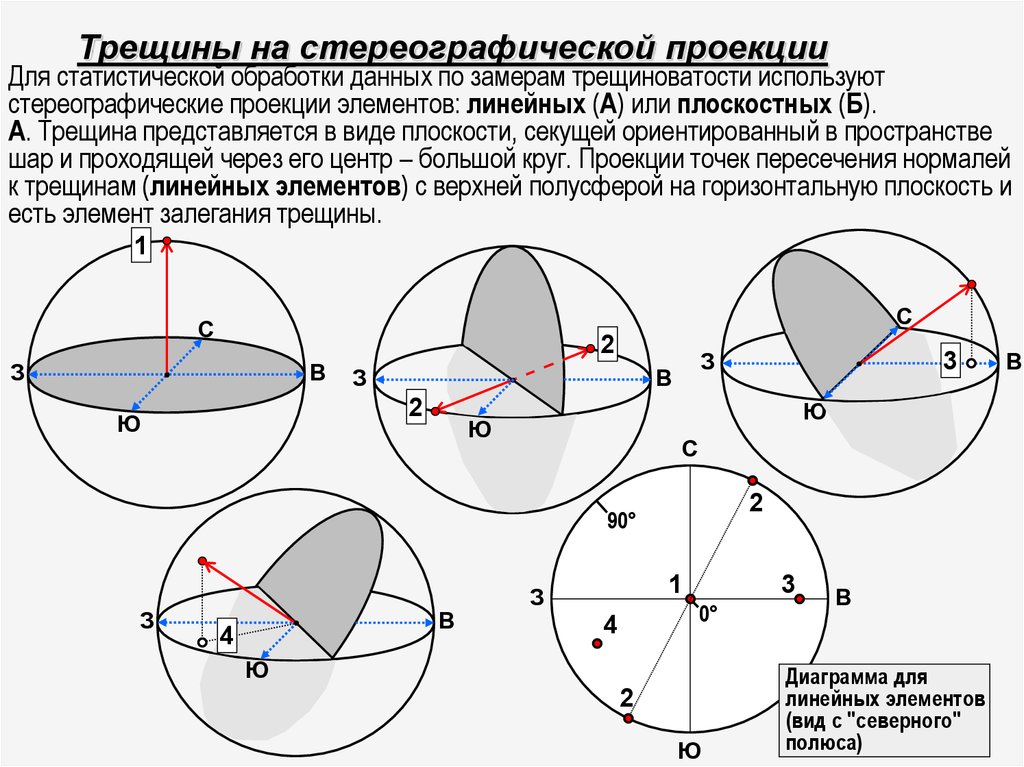
52. Трещины на стереографической проекции

Для статистической обработки данных по замерам трещиноватости используют
стереографические проекции элементов: линейных (А) или плоскостных (Б).
А. Трещина представляется в виде плоскости, секущей ориентированный в пространстве
шар и проходящей через его центр – большой круг. Проекции точек пересечения нормалей
к трещинам (линейных элементов) с верхней полусферой на горизонтальную плоскость и
есть элемент залегания трещины.
1
C
C
2
З
В
З
2
Ю
З
В
Ю
Ю
С
2
90°
З
В
4
3
1
З
3
0°
4
Ю
2
Ю
В
Диаграмма для
линейных элементов
(вид с "северного"
полюса)
В

53.

Б. Трещина представляется в виде плоскости, секущей ориентированный в пространстве
шар и проходящей через его центр – большой круг. Проекции больших кругов
(плоскостных элементов) верхней полусферы на горизонтальную плоскость
представляют собой
дуги разной кривизны.
3
C
2
З
C
З
З
В
В
1
В
Ю
Ю
Ю
Проекция линии
пересечения больших
кругов проводится от
точки пересечения дуг к
центру круга!
С
1
4
4
З
В
Ю
З
Диаграмма
для плоскостных 3
элементов (вид с
"северного"
полюса)
В
2
Ю

54.

С
В
З
Ю

55.

С
В
З
Ю

56. Трансформные разломы, или сдвиги Вилсона

Трансформные разломы со структурнокинематической точки зрения имеют ряд
особенностей, резко отличающих их от
сдвигов Андерсона.
Главное отличие сдвигов Вилсона от
андерсоновских заключается в том,
что они разделяют блоки, площадь
которых не постоянна, а изменяется –
либо увеличивается в кулисно
расположенных узких активных зонах
разрастания, либо уменьшается в
ограниченных по простиранию узких
активных зонах поглощения.
Трансформные разломы представляют собой
согласующие элементы активных зон, они
образуют системы параллельных сдвигов
часто с противоположным направлением
смещения, которые заканчиваются в
активных структурах растяжения или сжатия

57.

Выделяют три основных типа вилсоновских сдвигов,
различающихся по структурно-кинематическим
особенностям (по Вилсону):
1) Сдвиги типа хребет – хребет (R-R);
2) Сдвиги типа дуга – дуга (А-А);
3) Сдвиги типа хребет – дуга (R-A).
Дж. Тузо Вилсон
1908-1993
Названия типам трансформных разломов
дано по наиболее типичным структурам, которые они представляют:
Трансформы типа хребет – хребет (по Арк.В. Тевелеву – Е-трансформы –
от extension – растяжение) соединяют соседние отрезки срединно-океанических
хребтов, т.е. зон разрастания (зон спрединга).
Трансформы типа хребет – дуга (М-трансформы – от mix – смесь)
соединяют срединно-океанические хребты, т.е. зоны разрастания (зоны
спрединга) и островные дуги, т.е. зоны поглощения (зоны субдукции).
Трансформы типа дуга – дуга (С-трансформы – от compression – сжатие)
соединяют отрезки островных дуг, т.е. зон поглощения (зон субдукции).

58. Трансформы типа хребет – хребет

Трансформные разломы
типа хребет – хребет
(Е-трансформы)
Атлантического океана

59. Основные элементы трансформ типа хребет–хребет

Зона разрастания
Пассивный сегмент
("хвост")
Зона разрастания
Активный сегмент
Пассивный сегмент
("хвост")

60. Свойства трансформ типа хребет–хребет

1 – собственно сдвиговые движения присутствуют только в пределах
активного отрезка (сегмента) трансформного разлома;
2 – активный отрезок трансформного разлома расположен между зонами
разрастания, которые смещены изначально, т.е. досдвиговая граница
блоков является первичной;
3 – амплитуды смещения досдвиговых маркеров активного сегмента по всей
длине сдвига одинаковы;
4 – амплитуды смещения
маркеров могут
Зона разрастания
существенно превышать
длину трансформы;
Активный сегмент
5 – длина пассивных
сегментов увеличивается
при развитии трансформы;
6 – зоны разрастания
являются активными
элементами, т.к.
Зона разрастания
именно в них происходит
увеличение площади
блоков.

61.

Для наблюдателей, находящихся на разных крыльях разлома, но в
пределах одного блока, их относительные горизонтальные смещения
будут, естественно, нулевыми, поскольку пассивные отрезки
представляют собой сбросы!
Направление мгновенных смещений по сдвигу Вилсона в принципе
неопределенно!
const

62. Кинематика Е-трансформ

1 – собственно сдвиговые движения присутствуют только в пределах
активного отрезка (сегмента) трансформного разлома;
2 – активный отрезок трансформного разлома расположен между зонами
разрастания, которые смещены изначально, т.е. досдвиговая граница
блоков является первичной;
3 – амплитуды смещения досдвиговых маркеров активного сегмента по всей
длине сдвига одинаковы;
4 – амплитуды смещения
маркеров могут
Зона разрастания
существенно превышать
Трансформа
длину трансформы;
"активный сегмент"
5 – длина пассивных
сегментов увеличивается
при развитии трансформы;
6 – зоны разрастания
являются активными
элементами,
Зона разрастания
т.к. именно в них
происходит увеличение
площади блоков.

63. Трансформы типа дуга – дуга

Свойства и кинематика
С-трансформ в существенной
степени зависят от
взаиморасположения зон
поглощения, которые практически
всегда наклонны.
1
Т. Вилсон выделял три разновидности
трансформ типа дуга – дуга:
1 – моновергентные, т.е.
соединяющие зоны поглощения,
падающие в одну сторону;
2 – синвергентные, т.е.
соединяющие зоны поглощения,
падающие навстречу друг другу;
3 – антивергентные, т.е.
соединяющие зоны поглощения,
падающие друг от друга
2
3

64. Свойства Моновергентных C-трансформ

1 – собственно сдвиговые движения присутствуют только в пределах
активного отрезка (сегмента) трансформного разлома;
2 – трансформный разлом расположен между зонами поглощения, которые
смещены изначально, т.е. досдвиговая граница блоков является
первичной;
3 – длина активного сегмента постоянна;
4 – амплитуды смещения досдвиговых маркеров активного отрезка
одинаковы по всей длине сдвига;
5 – зоны поглощения
являются активными
элементами, т.к. именно в
них происходит
уменьшение площади
блоков
Зона
поглощения
Трансформа
Зона
поглощения

65. Особенности антивергентных С-трансформ

1 – собственно сдвиговые движения присутствуют только в пределах
трансформного разлома;
2 – трансформный разлом расположен между расходящимися зонами
поглощения, которые смещены изначально, т.е. досдвиговая граница
блоков является первичной;
3 – при развитии трансформы длина активного сегмента уменьшается
до нуля, а затем увеличивается;
4 – после прохождения нулевой точки маркеры, располагавшиеся вне
трансформы, попадают в область трансформы; амплитуды их
смещения могут быть любыми;
5 – зоны поглощения
являются активными
элементами, т.к.
именно в них
происходит уменьшение
площади блоков

66. Кинематика трансформ типа хребет – дуга

М-трансформы принципиально отличаются от остальных тем, что сопрягаемые
ими активные зоны находятся по одну сторону от трансформного разлома,
который, таким образом, оказывается как бы рельсом, вдоль которого
обмениваются массами (движениями) активные зоны.
Трансформа
1 – собственно сдвиговые
движения присутствуют
только в пределах
трансформы;
2 – трансформа
расположена между зонами
разрастания и поглощения;
3 – длина трансформы
постоянна
Зона
4 – амплитуды смещения
Зона
поглощения
разрастания
досдвиговых маркеров
активного отрезка
одинаковы по всей длине
сдвига;
5 – активными элементами являются и зоны разрастания,
и зоны поглощения

67. Кинематика трансформ типа хребет – дуга

М-трансформы принципиально отличаются от остальных тем, что сопрягаемые
ими активные зоны находятся по одну сторону от трансформного разлома,
который, таким образом, оказывается как бы рельсом, вдоль которого
обмениваются массами (движениями) активные зоны.
1 – собственно сдвиговые
Трансформа
движения присутствуют
только в пределах
трансформы;
2 – трансформа
расположена между зонами
разрастания и поглощения;
3 – длина трансформы
постоянна
4 – амплитуды смещения
Зона
досдвиговых маркеров
Зона
поглощения
разрастания
активного отрезка
одинаковы по всей
длине сдвига;
6 – При развитии М-трансформ возможно
5 – активными элементами
являются и зоны разрастания, погружение зоны разрастания под
неподвижную плиту в зоне поглощения
и зоны поглощения