Отношения следования и равносильности

1. Отношения следования и равносильности

2.

Импликацией предикатов А(х) и
В(х), заданных на множестве Х,
называется предикат А(х) В(х),
заданный на том же множестве,
который ложен лишь при тех
значениях х Х, при которых
А(х) истинен, а В(х) ложен.

3.

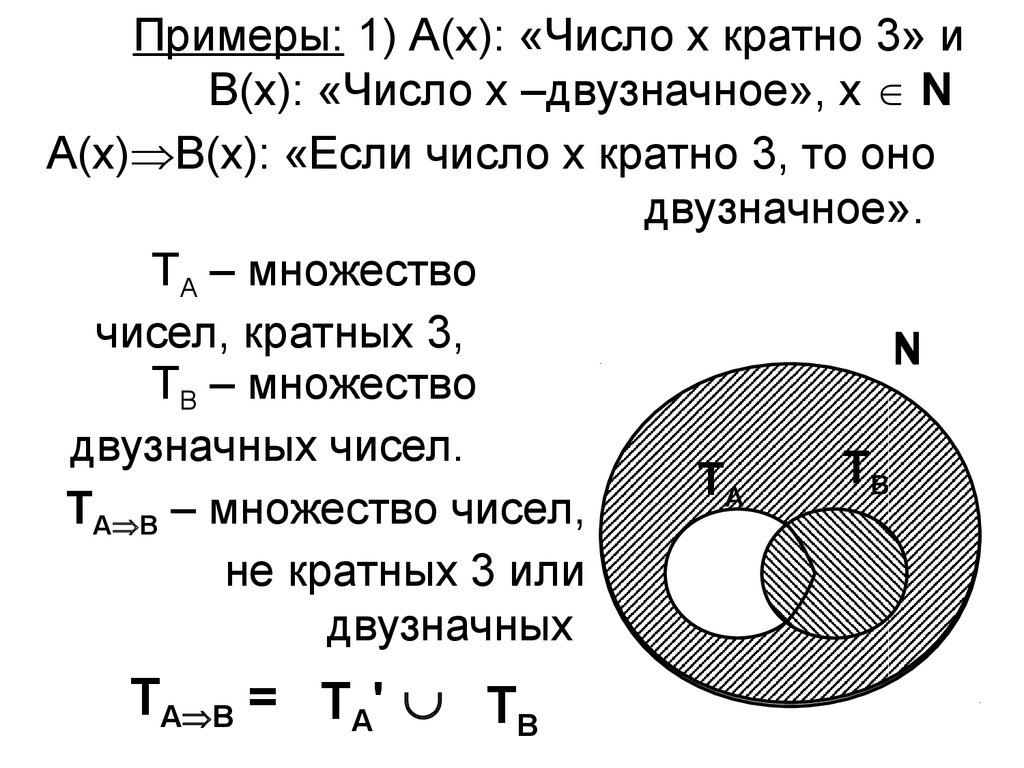
Примеры: 1) А(х): «Число х кратно 3» и
В(х): «Число х –двузначное», х N
А(х) В(х): «Если число х кратно 3, то оно
двузначное».
ТА – множество
чисел, кратных 3,
N
ТВ – множество
двузначных чисел.
ТТВ
ТТАА
В
ТА В – множество чисел,
не кратных 3 или
двузначных
ТА В = ТА' ТВ

4.

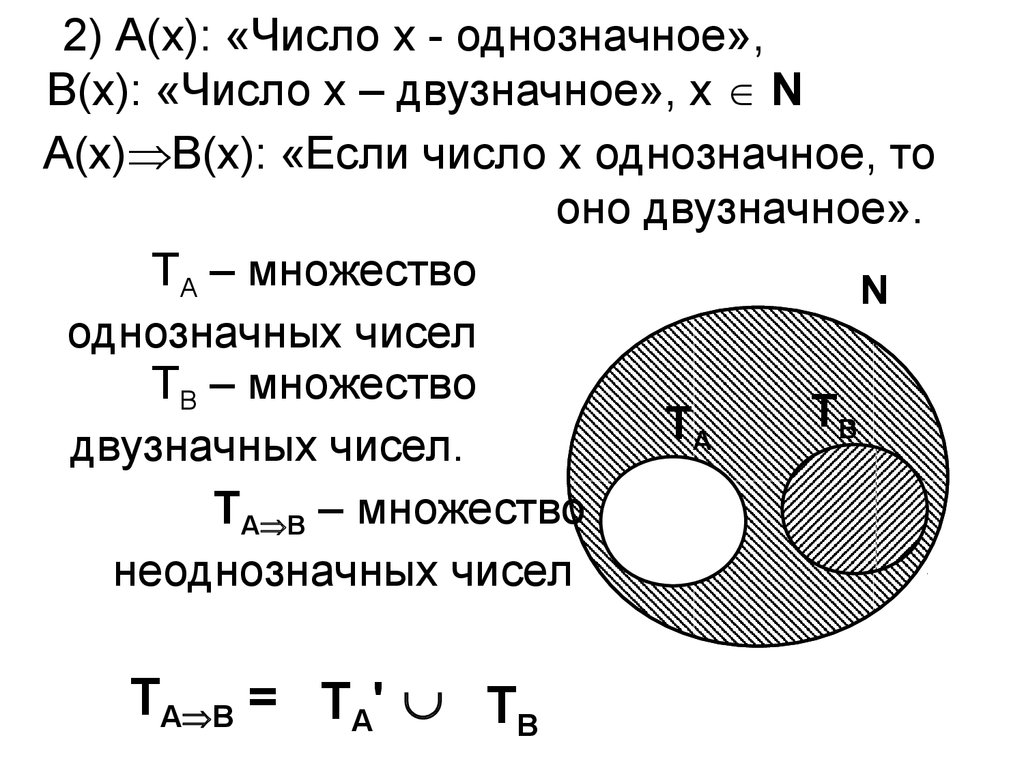
2) А(х): «Число х - однозначное»,
В(х): «Число х – двузначное», х N
А(х) В(х): «Если число х однозначное, то
оно двузначное».
ТА – множество
N
однозначных чисел
ТВ – множество
ТВ
Т
А
двузначных чисел.
ТА В – множество
неоднозначных чисел
ТА В = ТА' ТВ

5.

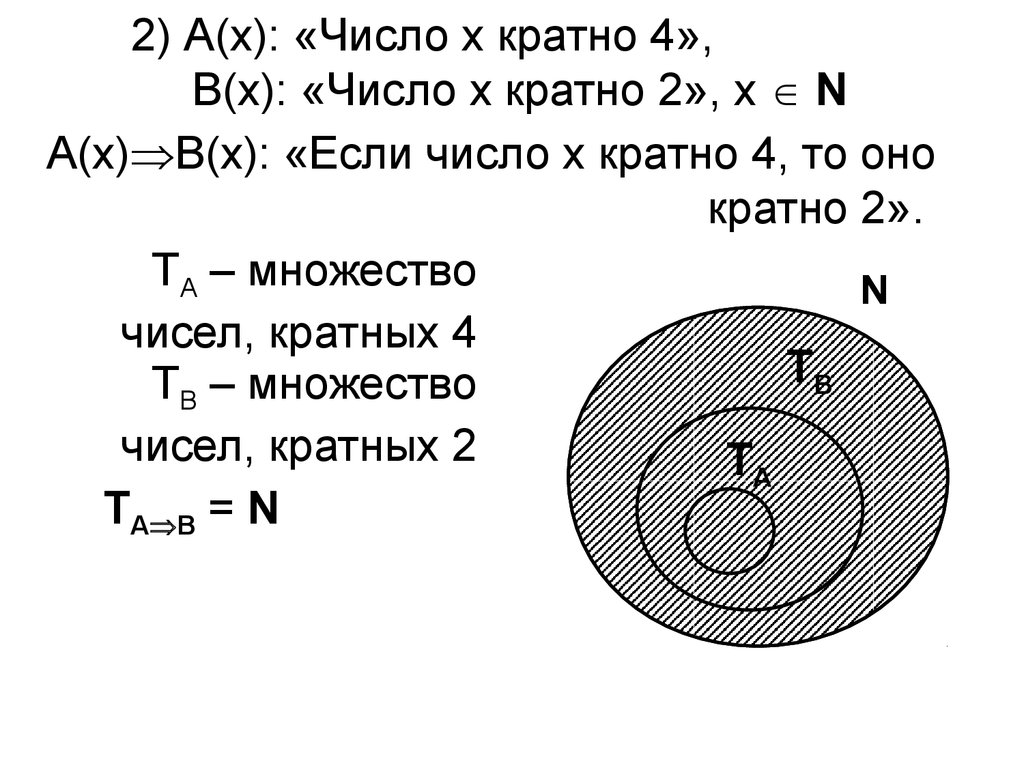
2) А(х): «Число х кратно 4»,
В(х): «Число х кратно 2», х N
А(х) В(х): «Если число х кратно 4, то оно
кратно 2».
ТА – множество
N
чисел, кратных 4
ТВ
ТВ – множество
чисел, кратных 2
ТА
ТА В = N

6.

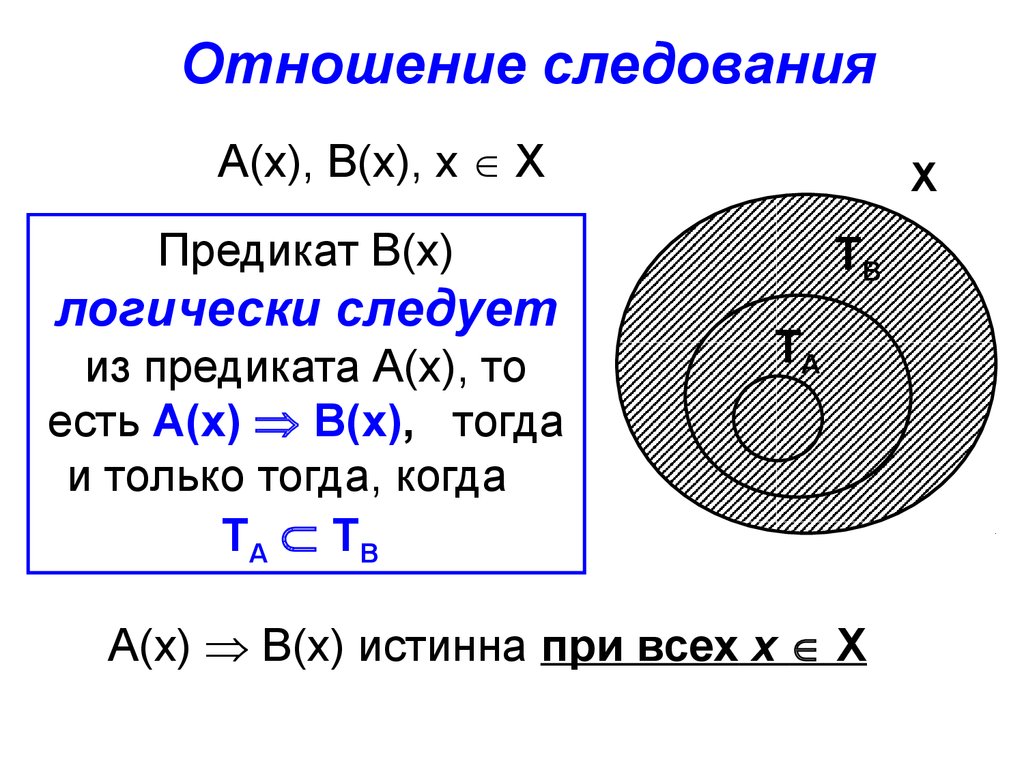
Отношение следования
А(х), В(х), х Х
Х
Предикат В(х)
логически следует
из предиката А(х), то
есть А(х) В(х), тогда
и только тогда, когда
ТА ТВ
ТВ
ТА
А(х) В(х) истинна при всех х Х

7.

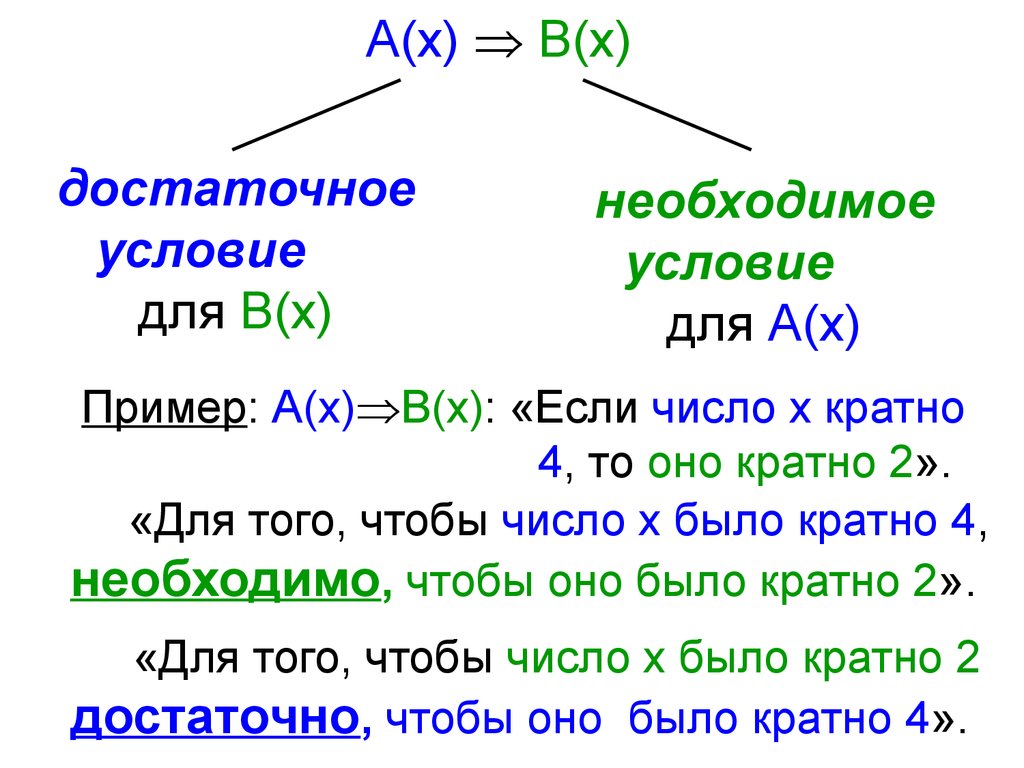
А(х) В(х)
достаточное
условие
для В(х)
необходимое
условие
для А(х)
Пример: А(х) В(х): «Если число х кратно
4, то оно кратно 2».
«Для того, чтобы число х было кратно 4,
необходимо, чтобы оно было кратно 2».
«Для того, чтобы число х было кратно 2
достаточно, чтобы оно было кратно 4».

8.

Эквиваленцией предикатов А(х) и
В(х), заданных на множестве Х,
называется предикат А(х) В(х),
заданный на том же множестве,
который истинен лишь при тех
значениях х Х, при которых
оба предиката истинны или оба
ложны.

9.

Отношение равносильности
Пусть даны предикаты А(х) и В(х), х Х.
Предикаты А(х) и В(х) равносильны,
то есть А(х) В(х), тогда и только
тогда, когда ТА = ТВ
Если предикаты А(х) и В(х) равносильны
на множестве Х, то эквиваленция
предикатов А(х) В(х) истинна при всех х
Х.

10.

Пример: А(х) «Число х делится на 10»,
В(х): «Запись числа х заканчивается
цифрой 0»
А(х) В(х): «Число х делится на 10 тогда и
только тогда, когда его запись
оканчивается 0»
ТА – множество чисел, кратных 10,
ТВ – множество чисел, запись которых
оканчивается цифрой 0.
ТА = ТВ, значит А(х) В(х),
то есть эквиваленция А(х) В(х)
истинна при всех х N

11.

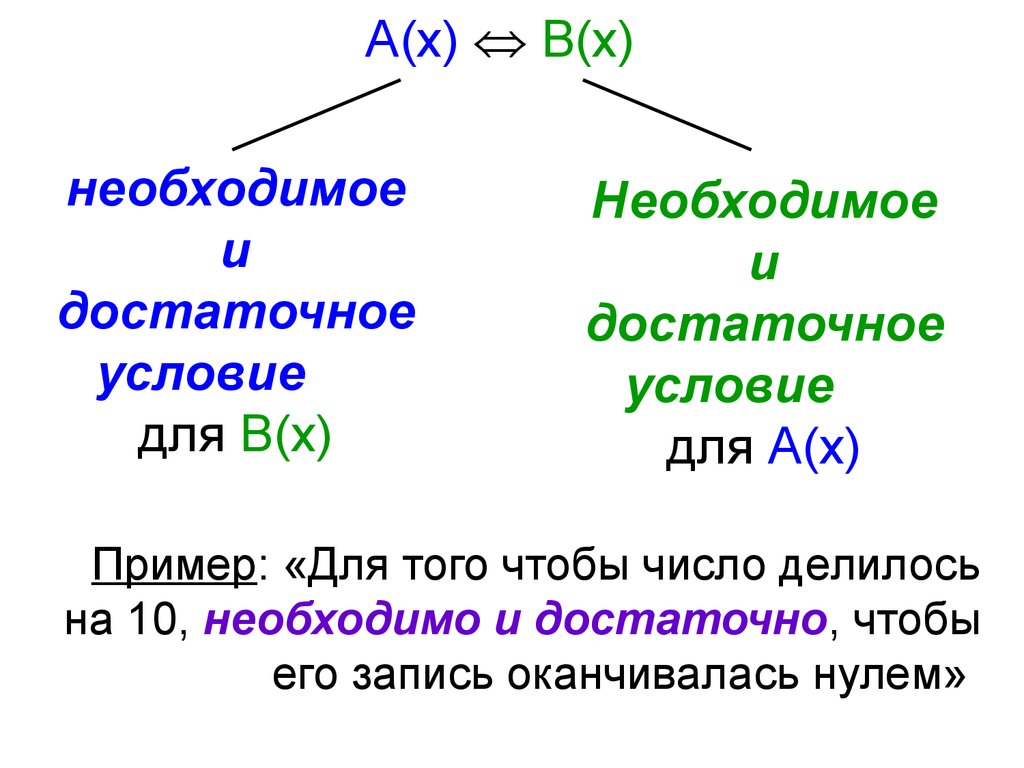
А(х) В(х)
необходимое
и
достаточное
условие
для В(х)
Необходимое
и
достаточное
условие
для А(х)
Пример: «Для того чтобы число делилось
на 10, необходимо и достаточно, чтобы
его запись оканчивалась нулем»

12.

Замечание.
Из
равносильности
предикатов А(х) и В(х) на некотором
множестве Х не следует, что предикаты,
выраженные теми же словами, окажутся
равносильными на другом множестве Y.
Пример:
А(х): «Все стороны четырехугольника
равны»,
В(х): «Диагонали четырехугольника
перпендикулярны».

13.

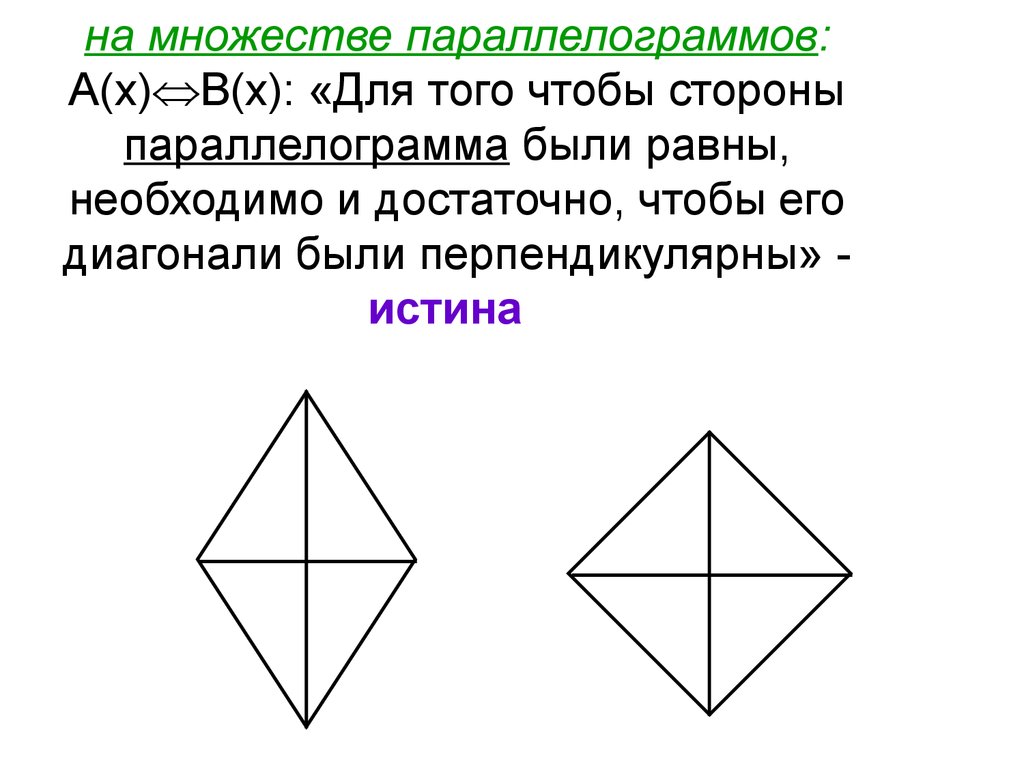
на множестве параллелограммов:
А(х) В(х): «Для того чтобы стороны
параллелограмма были равны,
необходимо и достаточно, чтобы его
диагонали были перпендикулярны» истина

14.

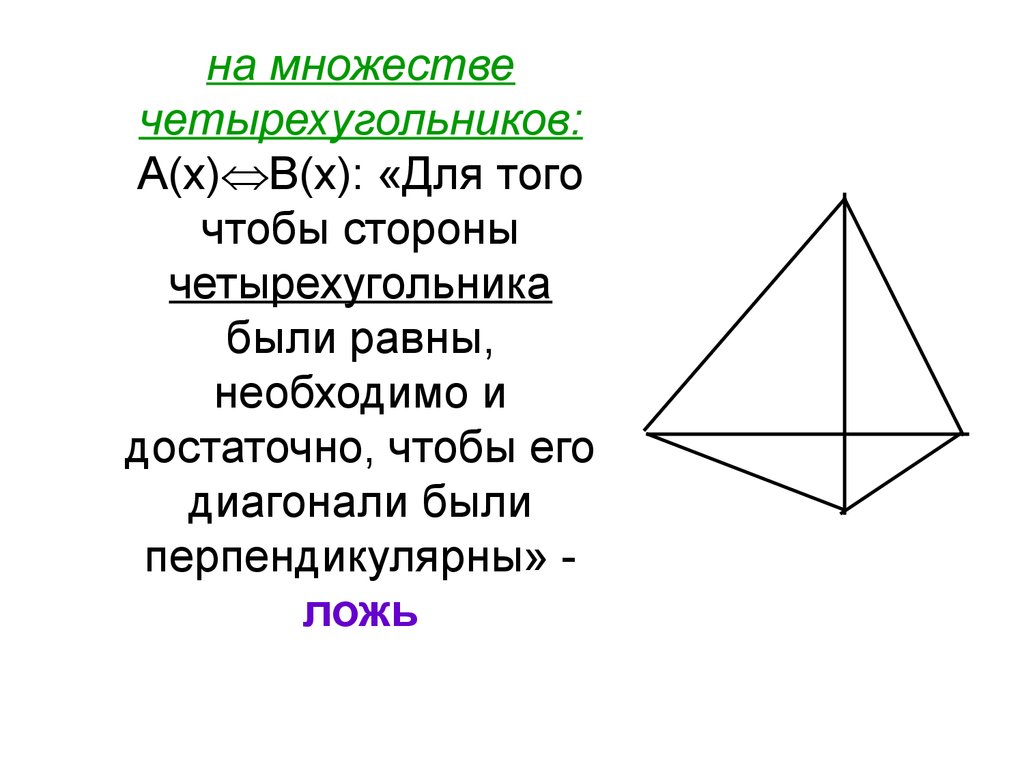
на множестве
четырехугольников:
А(х) В(х): «Для того
чтобы стороны
четырехугольника
были равны,
необходимо и
достаточно, чтобы его
диагонали были
перпендикулярны» ложь

15. Теоремы

16.

Теорема – это высказывание,
истинность которого
устанавливается посредством
рассуждения (доказательства).
Теорема - от греч. представление, зрелище

17.

С логической точки зрения теорема
представляет собой высказывание
А(х) В(х), где А(х) и В(х) – предикаты,
причем В(х) логически следует из
А(х), то есть В(х) обращается в истинное
высказывание при всех тех значениях х,
при которых А(х) истинен.
А(х) – условие теоремы,
В(х) – заключение теоремы.
Теорема может быть сформулирована с
помощью слов «если …, то…», «следует»,
«необходимо», «достаточно», а также без
использования этих слов.

18.

Пример: «В прямоугольнике
диагонали равны».
Если четырехугольник является
прямоугольником, то диагонали в нем равны
Из того, что четырехугольник является
прямоугольником следует, что его диагонали
равны
Для того чтобы в четырехугольнике диагонали
были равны, достаточно, чтобы он был
прямоугольником
Для того чтобы четырехугольник был
прямоугольником, необходимо, чтобы его
диагонали были равны

19.

Кроме условия и заключения теорема
содержит разъяснительную часть
(словесно она обычно не формулируется,
но всегда подразумевается, и при работе с
теоремой ее необходимо выделять).
В рассмотренном выше примере
разъяснительная часть следующая:
работаем на множестве всех
прямоугольников.

20.

В математике кроме теорем
используются предложения,
называемые правилами и формулами.
Пример: правило деления суммы на число:
«для того, чтобы разделить сумму на число,
можно разделить на это число каждое из
слагаемых и полученные результаты сложить»
(а + b) : с = а : с + b : с
Условие: а, b и с – целые неотрицательные
числа (с 0), а с и b с
Заключение: (а + b) : с = а : с + b : с

21.

А(х) В(х) – данная теорема
В(х) А(х) - теорема обратная данной
А( х) В( х) - теорема
противоположная данной
В ( х) А( х) - теорема
обратная
противоположной или
противоположная
обратной

22.

А(х) В(х): «Если сумма цифр числа
кратна 9, то и само число кратно 9»
В(х) А(х):«Если число кратно 9, то и
сумма цифр числа кратна 9»
А( х) В( х) : «Если сумма цифр числа
не кратна 9, то и число не
кратно 9»
В( х) А( х)
: «Если число не кратно 9,
то и сумма цифр числа не
кратна 9»

23.

А(х) В(х) = В( х) А( х)
В(х) А(х) = А( х) В( х)
закон контрапозиции

24.

Замечание. Если условие или заключение
данной теоремы представляет собой
конъюнкцию или дизъюнкцию, то чтобы
получить теорему противоположную
данной и обратную противоположной
(противоположную обратной), нужно
учитывать правила построения отрицания
конъюнкции или дизъюнкции.

25.

ПРИМЕР:
А(х) В(х): «ЕСЛИ ЧИСЛО ДЕЛИТСЯ НА 3 И НА 5,
ТО ОНО ДЕЛИТСЯ НА 15»
А( х) В( х) : «Если число не делится на 3
или не делится на 5, то оно не
делится на 15»
В( х) А( х) : «Если число не делится на 15, то
оно не делится на 3 или не
делится на 5»

26.

Если для данной теоремы А(х) В(х)
истинна обратная теорема В(х) А(х),
то их можно объединить в одну
А(х) В(х), и тогда в формулировке
будут использоваться слова
«необходимо и достаточно»,
«тогда и только тогда, когда»

27.

Пример:
А(х) В(х): «В равнобедренном
треугольнике углы при основании равны»
В(х) А(х): «Если в треугольнике углы при
основании равны, то
треугольник равнобедренный»

28.

А(х) В(х): «Для того, чтобы треугольник
был равнобедренным, необходимо и
достаточно, чтобы в нем углы при
основании были равны»
или
«Треугольник будет равнобедренным тогда
и только тогда, когда в нем углы при
основании будут равны»

29.

ЕСЛИ ТЕОРЕМА ИМЕЕТ ВИД
РАВНОСИЛЬНОСТИ А(Х) В(Х), ТО ЭТО
ЗНАЧИТ, ЧТО ОНА СОСТОИТ ИЗ ДВУХ
ВЗАИМНО ОБРАТНЫХ ТЕОРЕМ:
А(Х) В(Х) И В(Х) А(Х),
И, СЛЕДОВАТЕЛЬНО, ЕЕ ДОКАЗАТЕЛЬСТВО
СВОДИТСЯ К ДОКАЗАТЕЛЬСТВУ ДВУХ
УКАЗАННЫХ ТЕОРЕМ

30.

Упражнения:
1. Выделите условие и заключение в каждой из
следующих теорем:
а) Диагонали прямоугольника равны.
б) Равенство треугольников есть достаточное условие их
равновеликости.
2. Для данной теоремы сформулируйте обратную,
противоположную и обратную противоположной
теоремы : «Диагонали ромба взаимно
перпендикулярны».
3. Покажите, что следующая теорема является
объединением двух теорем: «На 5 делятся те и только
те числа, запись которых оканчивается
цифрой 0 или цифрой 5»