Похожие презентации:
Моделирование марковских случайных процессов
1. Моделирование марковских случайных процессов
Российский государственный университет нефти и газа (НИУ)имени И.М. Губкина
Кафедра автоматизированных систем управления
Моделирование марковских
случайных процессов
асс. Мухина А. Г.
г. Москва
2018 г.
2. Основы теории случайных процессов
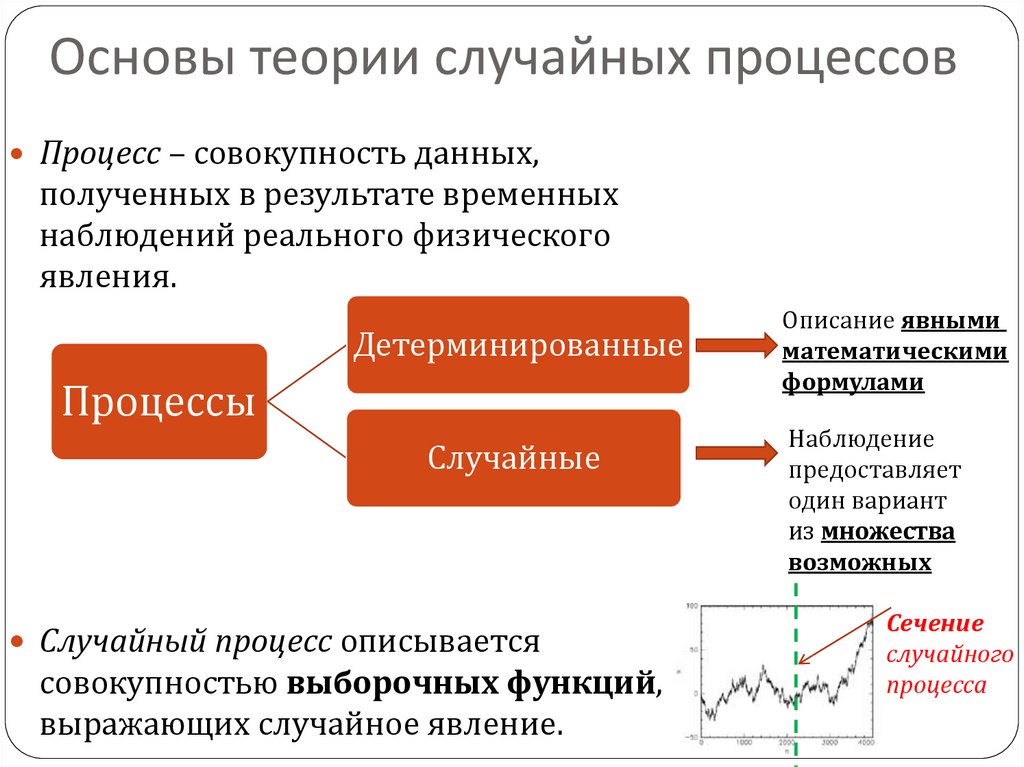
Процесс – совокупность данных,полученных в результате временных
наблюдений реального физического
явления.
Детерминированные
Процессы
Случайные
Случайный процесс описывается
совокупностью выборочных функций,
выражающих случайное явление.
Описание явными
математическими
формулами
Наблюдение
предоставляет
один вариант
из множества
возможных
Сечение
случайного
процесса
3. Марковский случайный процесс
«То, что мы называем случайностями — всего лишьзакономерности, которые мы не в состоянии расшифровать»
Случайный процесс называется марковским, если для
любого момента времени t0 вероятностные характеристики
процесса в будущем зависят только от его текущего
состояния x(t0) и не зависят от того, когда и как система
пришла в это состояние.
Для марковского процесса будущее зависит от прошлого
только через настоящее.
S0
t0
S1
t1
Марковский
процесс
S2
t2
t, с
С дискретными
состояниями
С непрерывным
временем
4. Поток событий и его характеристики
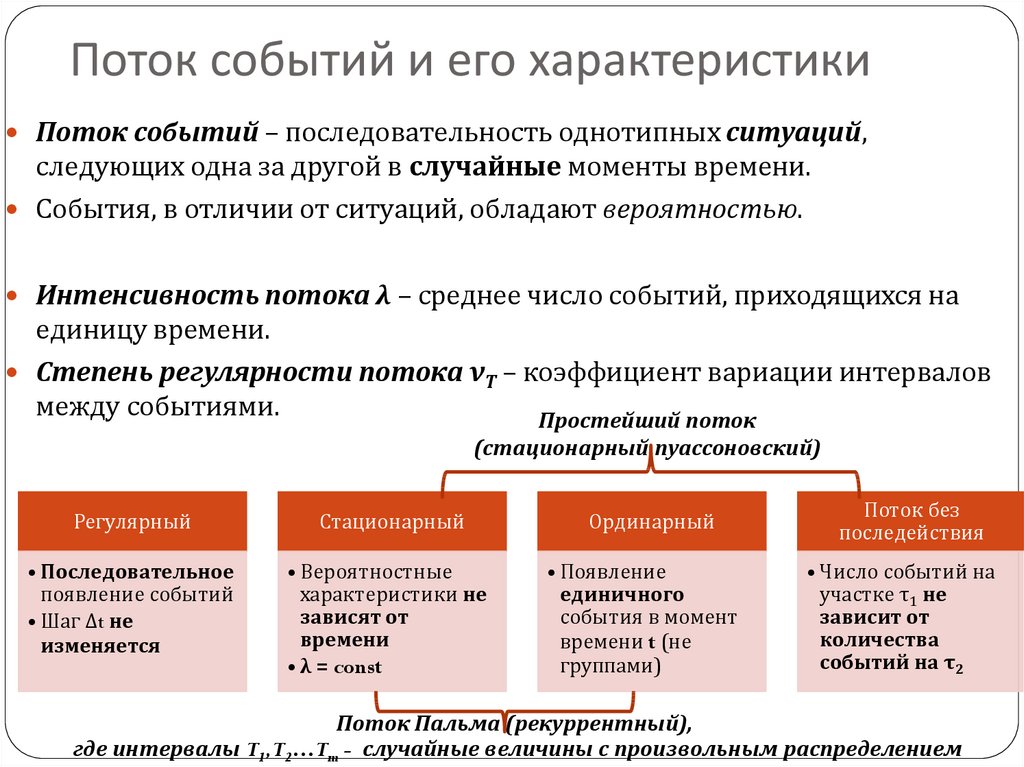
Поток событий – последовательность однотипных ситуаций,следующих одна за другой в случайные моменты времени.
События, в отличии от ситуаций, обладают вероятностью.
Интенсивность потока λ – среднее число событий, приходящихся на
единицу времени.
Степень регулярности потока νT – коэффициент вариации интервалов
между событиями.
Простейший поток
(стационарный пуассоновский)
Регулярный
Стационарный
• Последовательное
появление событий
• Шаг ∆t не
изменяется
• Вероятностные
характеристики не
зависят от
времени
• λ = const
Ординарный
• Появление
единичного
события в момент
времени t (не
группами)
Поток без
последействия
• Число событий на
участке τ1 не
зависит от
количества
событий на τ2
Поток Пальма (рекуррентный),
где интервалы T1,T2…Tm - случайные величины с произвольным распределением
5. К математическому моделированию марковских процессов
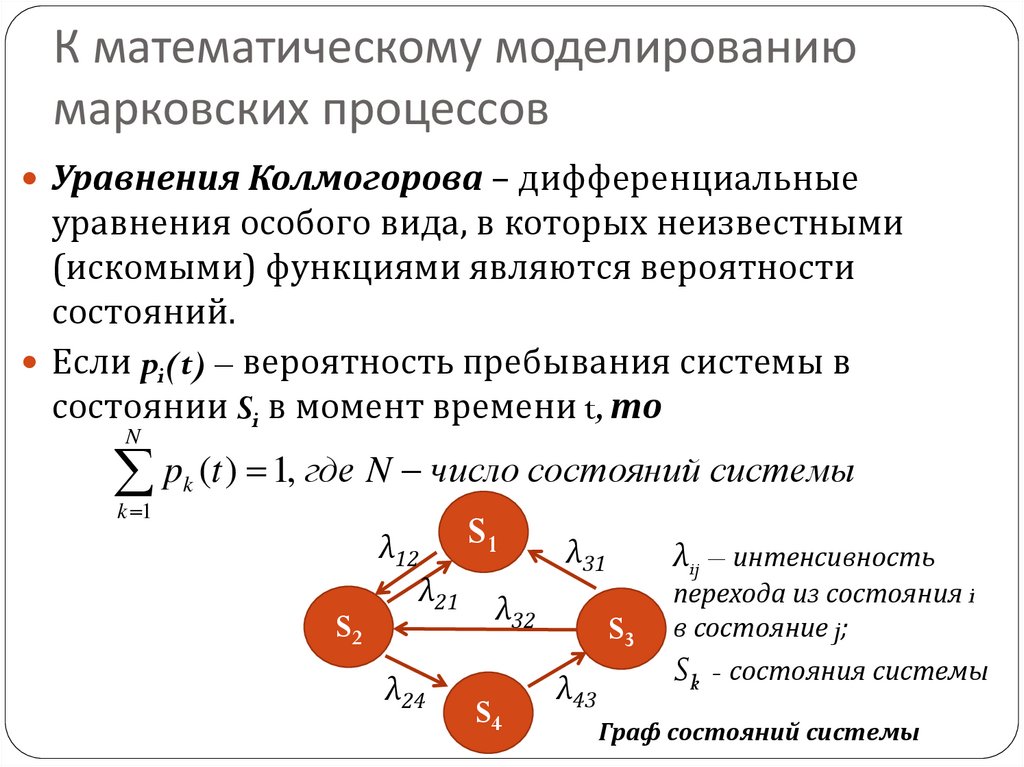
Уравнения Колмогорова – дифференциальныеуравнения особого вида, в которых неизвестными
(искомыми) функциями являются вероятности
состояний.
Если pi(t) – вероятность пребывания системы в
состоянии Si в момент времени t, то
N
p (t ) 1, где N число состояний системы
k 1
k
λ12 S1
λ31
λ21
λ32
S2
S3
λ24
S4
λ43
λij – интенсивность
перехода из состояния i
в состояние j;
Sk - состояния системы
Граф состояний системы
6. Распределение вероятностей состояний. Финальные вероятности
Для решения уравнений Колмогорова необходимо задатьначальные условия, к примеру: p1(0)=1 – система в состоянии S1 в
момент времени t0.
Распределение
вероятностей состояний.
Финальные вероятности – пределы вероятности состояний
системы при t→∞, не зависящие от начального состояния системы: p1,
p2, p3, p4. При этом:
1) pi = const;
2) pi - среднее относительное время пребывания системы в состоянии Sk
7. Системы массового обслуживания
Системы, на вход которых подаётся случайный потокоднотипных заявок (событий), обрабатываемых одним или
несколькими однотипными каналами (устройствами).
Одноканальные
Многоканальные
СМО с очередью
Параметры эффективности СМО (средние показатели):
1. Nr – число заявок;
2.
3.
4.
5.
Nc – число занятых каналов;
Lq - длина очереди;
Thold – время ожидания в очереди;
Ndr – число заявок, получивших отказ в обслуживании.
8. Модель n-канальной СМО с отказами
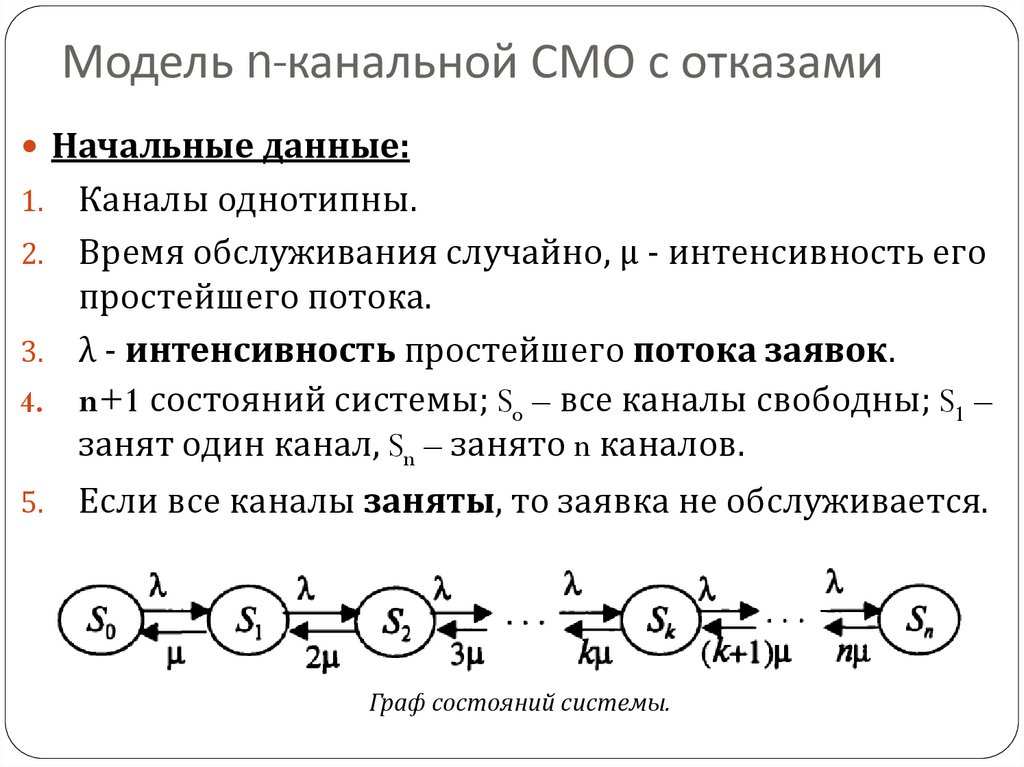
Начальные данные:Каналы однотипны.
2. Время обслуживания случайно, µ - интенсивность его
простейшего потока.
3. λ - интенсивность простейшего потока заявок.
4. n+1 состояний системы; So – все каналы свободны; S1 –
занят один канал, Sn – занято n каналов.
1.
5.
Если все каналы заняты, то заявка не обслуживается.
Граф состояний системы.
9. Параметры СМО. Формулы Эрланга.
Приведённая интенсивность заявок:Вероятность пребывания системы в состоянии Sk:
pk
k
k!
n
p0 , где p0 (
k 0
k
k!
Вероятность отказа системы:
pотк pn
n
p0
n!
Вероятность обслуживания заявки:
Q 1 pотк 1
n
n!
p0
) 1
Формулы Эрланга
10. Показатели эффективности каналов СМО
Абсолютная пропускная способность (среднее числозаявок, обслуженных в единицу времени):
A Q
Среднее число загруженных каналов:
N з p1 2 p2 ... npn
Коэффициент загрузки одного канала:
Nз
Кз
, где n общее число каналов.
n
11. Резюме по системам массового обслуживания
Основными элементами СМО являются:1) входной поток заявок;
2) очередь;
3) каналы обслуживания;
4)выходной поток заявок (обслуженные заявки).
Роль каналов выполняют приборы, операторы, продавцы,
линии связи.
Предназначение СМО состоит в обслуживании потока заявок
(требований), представляющих последовательность
событий, поступающих нерегулярно и в заранее
неизвестные и случайные моменты времени.
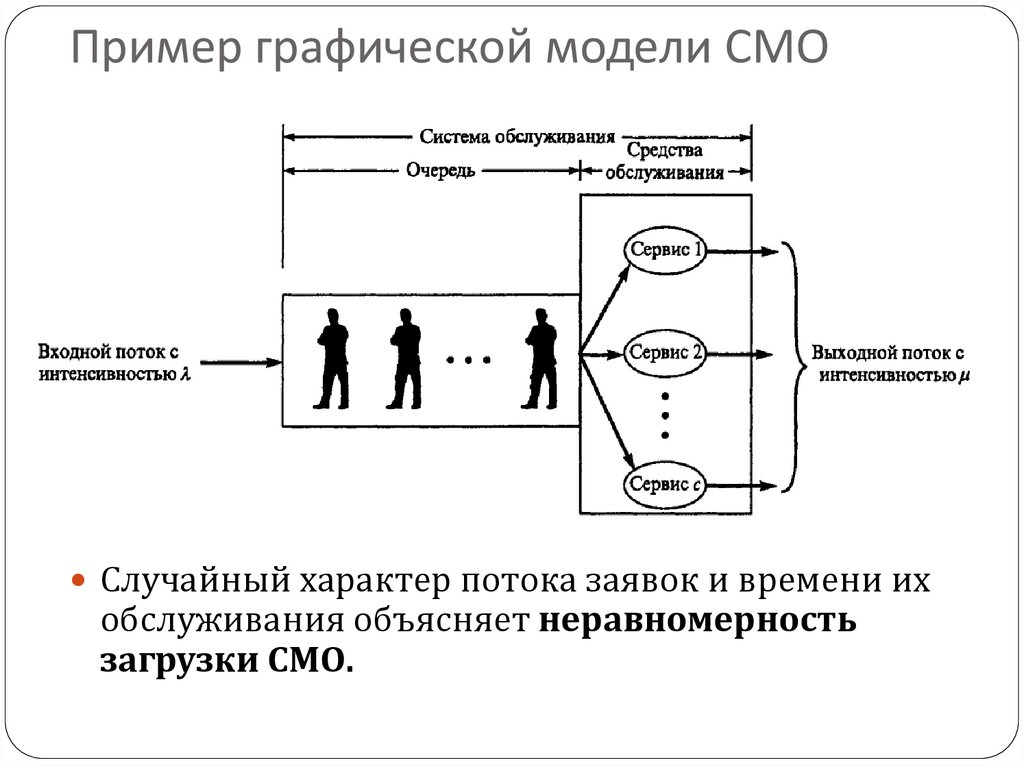
12. Пример графической модели СМО
Случайный характер потока заявок и времени ихобслуживания объясняет неравномерность
загрузки СМО.
13. Примеры применения СМО в нефтегазовой отрасли
Технология реализации СПГ.Распределённые компрессорные станции.
Линейное производственное управление магистральными газопроводами.









 Математика
Математика








