Интеллектуальный поиск путей на графах. Обзор алгоритмов, применение в компьютерных играх

1.

Нижегородский государственный университет им. Н.И. Лобачевского
Национальный исследовательский университет
Факультет ВМК
Кафедра МО ЭВМ
Интеллектуальный поиск путей на графах.
Обзор алгоритмов, применение в
компьютерных играх
Выполнили:
Сударикова М.А.
Филичев Т.А.
2011г.

2. Введение

2
Алгоритм поиска пути на графе, начиная с некоторой
стартовой вершины, исследует достижимые из нее узлы до тех
пор, пока не будет найдена конечная вершина.
Задача поиска путей на графе обычно возникает при
необходимости составления оптимального маршрута, и может
встречаться в экономике, робототехнике и компьютерных играх
(стратегии реального времени).
В практике компьютерных игр часто возникает необходимость
проложить курс из одной в другую точки игрового поля с
отмеченными на нем непроходимыми областями. Примером
может стать движение бота к персонажу игрока.
Сударикова М.А. Филичев Т.А.
Поиск путей на графах. Обзор алгоритмов.
2

3. Основные понятия

3
Путем называется последовательность вершин
в
графе G = (V, Е), такая что каждое из ребер
находится в
наборе Е .
Вес пути это сумма весов каждого ребра пути:
Вес (и, v) кратчайшего пути из вершины и в вершину v —
это минимум весов всех возможных путей из и в v.
Кратчайшим путем называется любой путь, вес которого
равен весу кратчайшего пути
Сударикова М.А. Филичев Т.А.
Поиск путей на графах. Обзор алгоритмов.
3

4. Дискретная модель

4
На карту накладывается
дискретная сетка
Перемещение по карте -
перемещение по клеткам сетки
Математическая модель -
ориентированный граф, вершины
которого соответствуют клеткам, а
рёбра возможностям перехода из
одной клетки в другую. Каждому
ребру можно назначить стоимость
перехода
Сударикова М.А. Филичев Т.А.
- препятствие
- свободная клетка
Поиск путей на графах. Обзор алгоритмов.
4

5. Непрерывная модель

5
Положение объектов на
карте определяется их
геометрической формой и
взаимным
расположением
Вводится набор
абстракций, например:
• точки видимости (на
рисунке)
• выпуклые полигоны
• квадрантные деревья
Сударикова М.А. Филичев Т.А.
Поиск путей на графах. Обзор алгоритмов.
5

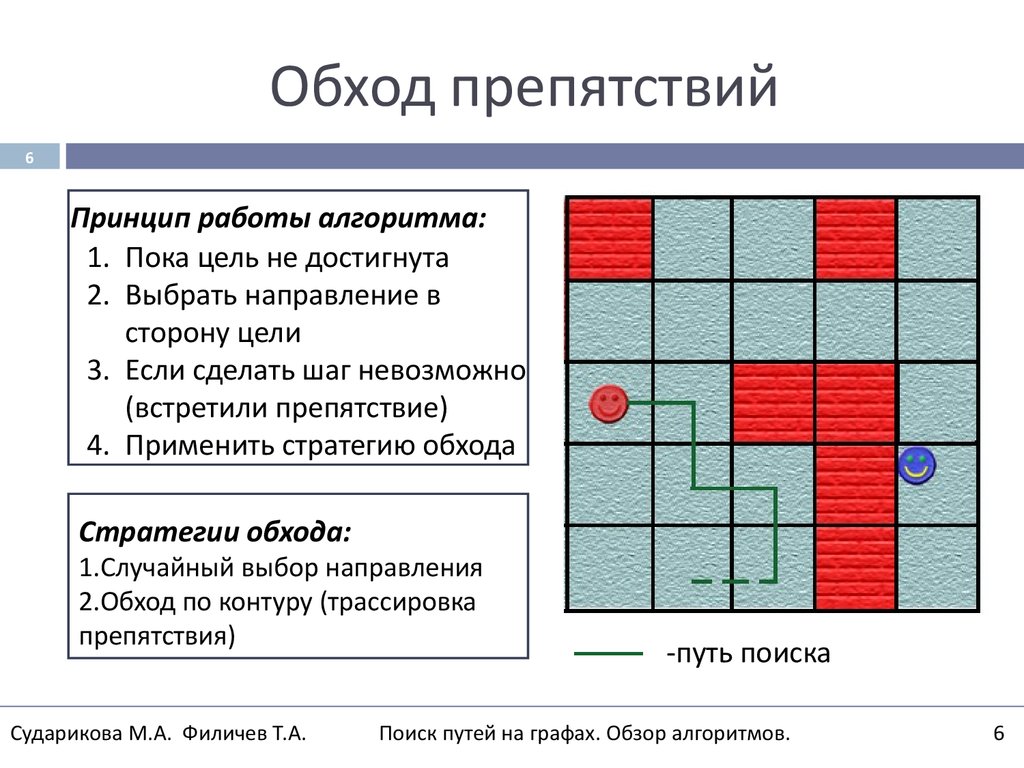
6. Обход препятствий

6
Принцип работы алгоритма:
1. Пока цель не достигнута
2. Выбрать направление в
сторону цели
3. Если сделать шаг невозможно
(встретили препятствие)
4. Применить стратегию обхода
Стратегии обхода:
1.Случайный выбор направления
2.Обход по контуру (трассировка
препятствия)
Сударикова М.А. Филичев Т.А.
-путь поиска
Поиск путей на графах. Обзор алгоритмов.
6

7. Обход препятствий

7
Достоинства:
1. Простота реализации
2. Учет взаимного
расположения стартовой и
финишной точки на карте
Недостатки:
1.При неверном выборе стратегии
обхода препятствий результат
может быть не получен
2.Алгоритм не применим на случай
взвешенных областей
Сударикова М.А. Филичев Т.А.
-путь поиска
Поиск путей на графах. Обзор алгоритмов.
7

8. Поиск в ширину

8
Поиск в ширину — обход графа, который посещает все вершины,
достижимые из данной исходной вершины. Порядок посещения вершин
определяется расстоянием от исходной вершины до каждой вершины графа.
Процедура поиска в ширину
Procedure BFS(a)
Q –очередь открытых вершин
V(x) – вершины, смежные с x
1. посетить вершину a
2. a→Q;
3. x←Q
4. for y∈V(x) do
5. исследовать ребро (x,y)
6. if вершина y новая
7. then посетить вершину y
8. y→Q
Сударикова М.А. Филичев Т.А.
Время работы процедуры BFS(a) есть
O(m), где m - число ребер в компоненте
связности, содержащей вершину.
Максимальное число
ребер
,
т.е. сложность
Для графов с небольшим числом ребер
предпочтительнее задание графа списками
смежности
Если веса ребер одинаковы, то поиск в
ширину находит кратчайший путь
Поиск путей на графах. Обзор алгоритмов.
8

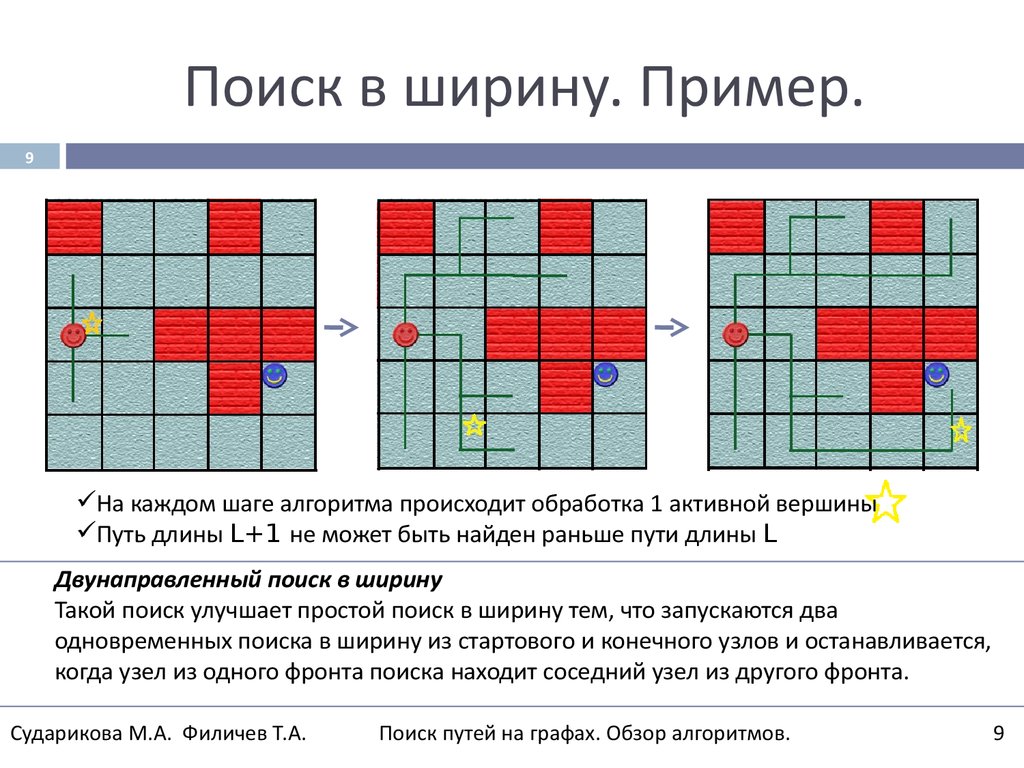
9. Поиск в ширину. Пример.

9
На каждом шаге алгоритма происходит обработка 1 активной вершины
Путь длины L+1 не может быть найден раньше пути длины L
Двунаправленный поиск в ширину
Такой поиск улучшает простой поиск в ширину тем, что запускаются два
одновременных поиска в ширину из стартового и конечного узлов и останавливается,
когда узел из одного фронта поиска находит соседний узел из другого фронта.
Сударикова М.А. Филичев Т.А.
Поиск путей на графах. Обзор алгоритмов.
9

10. Поиск в глубину

10
Поиск в глубину - обход графа, при этом на очередном шаге выбирается смежная с
текущей еще не посещенная вершина, пока не будет достигнута вершина у которой
нет смежных не посещенных вершин. Затем поиск возвращается к предыдущей
вершине и продолжает идти вдоль еще не исследованных ребер, выходящих из
этой вершины.
Время работы процедуры DFS(a)
Процедура поиска в глубину
Procedure DFS(a)
есть O(m), где m - число ребер в
S –стек открытых вершин
компоненте связности, содержащей
1. посетить вершину a; a→S;
вершину или
, n – число
2. While S!=∅
вершин в графе.
Путь, найденный поиском в глубину
3. x = top(S)
4. if ∃ неисследованное ребро (x,y)
не обязательно является
5. исследовать ребро (x,y)
кратчайшим.
При выборе очередной вершины
6. if вершина y новая
7. then посетить вершину y; y→S
можно учитывать оставшееся
8. Если нет неисследованных ребер
расстояние до цели.
x←S;
Сударикова М.А. Филичев Т.А.
Поиск путей на графах. Обзор алгоритмов.
10

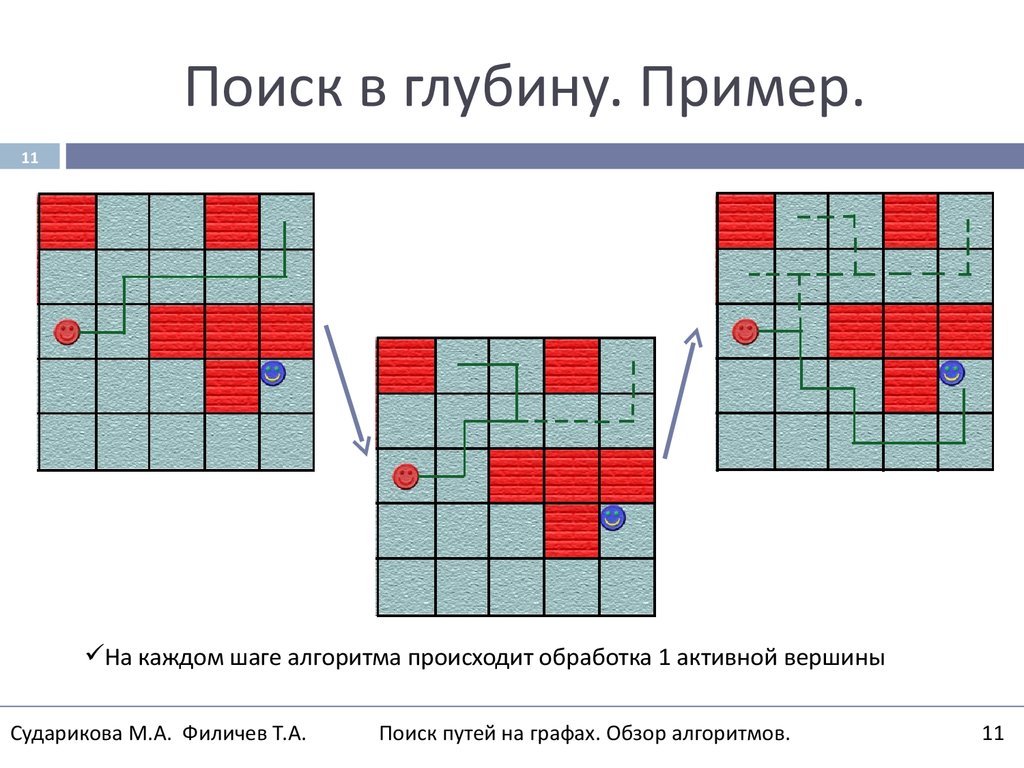
11. Поиск в глубину. Пример.

11
На каждом шаге алгоритма происходит обработка 1 активной вершины
Сударикова М.А. Филичев Т.А.
Поиск путей на графах. Обзор алгоритмов.
11

12. Алгоритм Дейкстры

12
Алгоритм Дейкстры находит все кратчайшие пути взвешенного графа с
неотрицательными весами из исходной вершины до каждой вершины графа,
последовательно наращивая множество вершин S, для которых известен
кратчайший путь
Алгоритм:
В общем случае сложность алгоритма
Q – приоритетная очередь
1. ∀x∈E d(x) = ∞; d(a) = 0;
На каждом шаге для вершин, изъятых
a→Q
из очереди уже найден кратчайший
2. while Q≠∅
путь.
3. x = min(Q); // x←Q выбираем Примени для использования во
элемент с минимальной меткой.
взвешенных областях
4. for y ϵ V(x)
Игнорирует направление к цели
5. if y – новая, d(y) = d(x)
+w(x,y), y→Q
6. else d(y) = min(d(y), d(x)
+w(x,y));
Сударикова
М.А. Филичев Т.А.
Поиск путей на графах. Обзор алгоритмов.
12

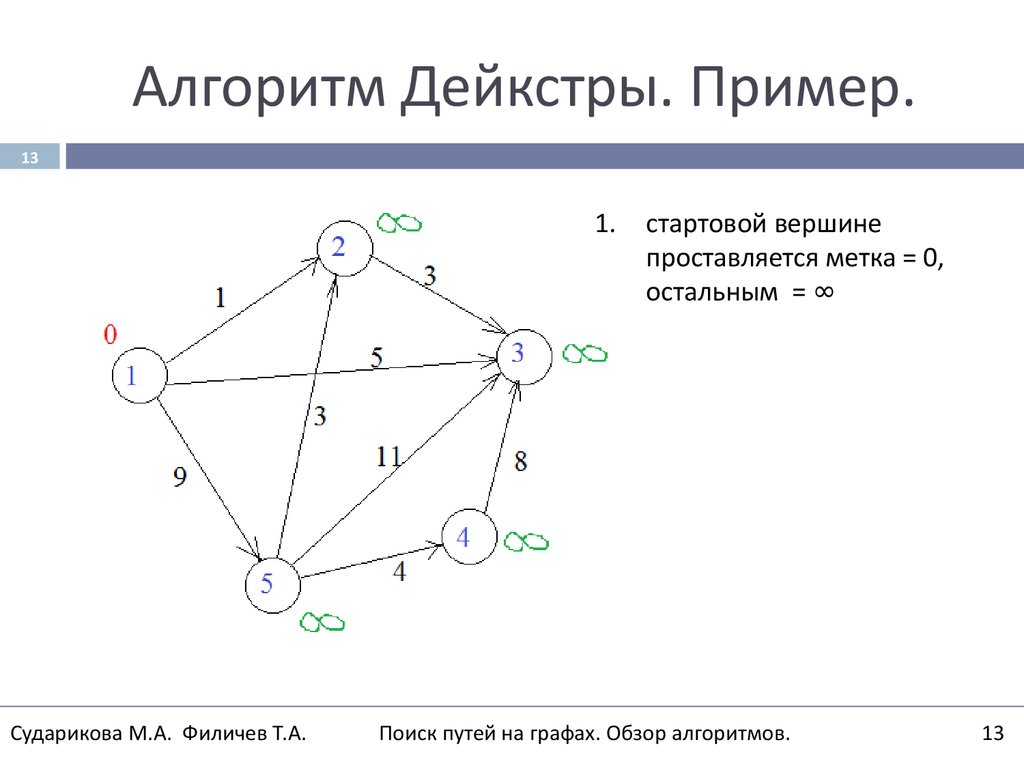
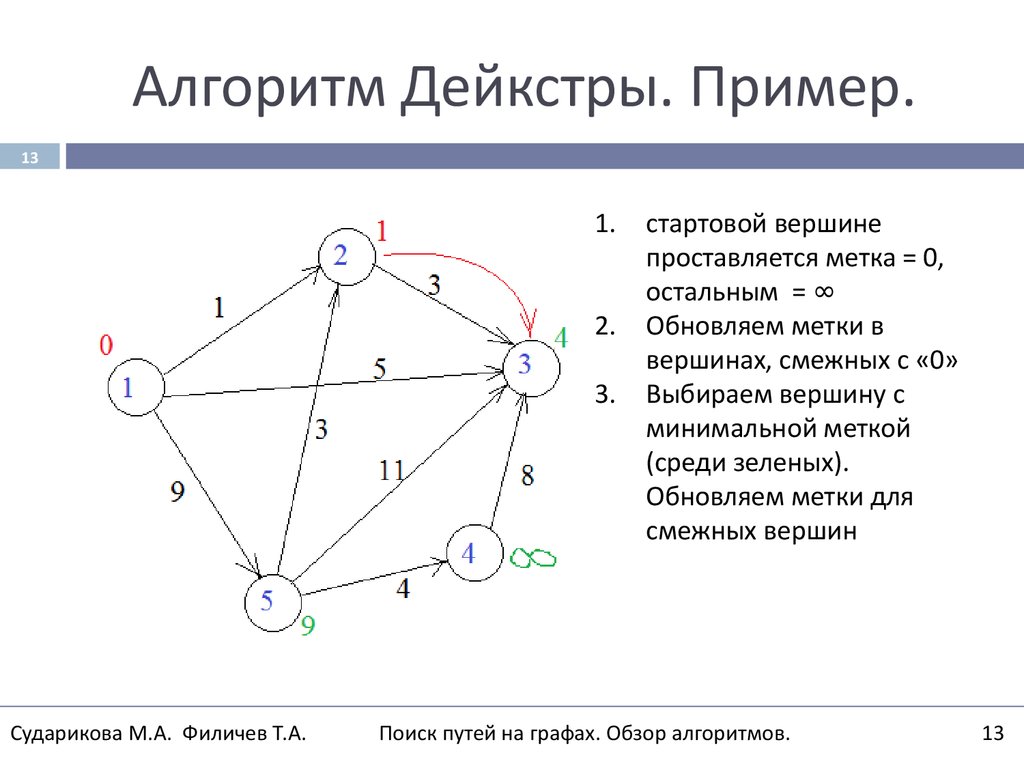
13. Алгоритм Дейкстры. Пример.

13
1.
Сударикова М.А. Филичев Т.А.
стартовой вершине
проставляется метка = 0,
остальным = ∞
Поиск путей на графах. Обзор алгоритмов.
13

14. Алгоритм Дейкстры. Пример.

13
1.
2.
Сударикова М.А. Филичев Т.А.
стартовой вершине
проставляется метка = 0,
остальным = ∞
Обновляем метки в
вершинах, смежных с «0»
Поиск путей на графах. Обзор алгоритмов.
13

15. Алгоритм Дейкстры. Пример.

13
1.
2.
3.
Сударикова М.А. Филичев Т.А.
стартовой вершине
проставляется метка = 0,
остальным = ∞
Обновляем метки в
вершинах, смежных с «0»
Выбираем вершину с
минимальной меткой
(среди зеленых).
Обновляем метки для
смежных вершин
Поиск путей на графах. Обзор алгоритмов.
13

16. Алгоритм Дейкстры. Пример.

13
1.
2.
3.
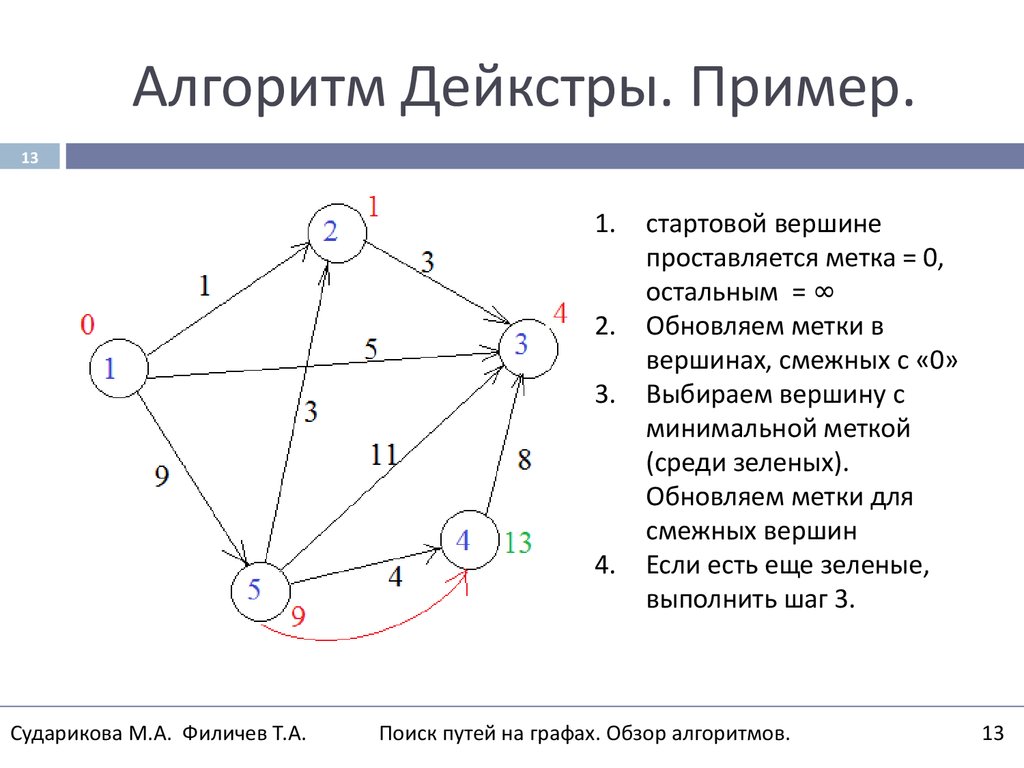
4.
Сударикова М.А. Филичев Т.А.
стартовой вершине
проставляется метка = 0,
остальным = ∞
Обновляем метки в
вершинах, смежных с «0»
Выбираем вершину с
минимальной меткой
(среди зеленых).
Обновляем метки для
смежных вершин
Если есть еще зеленые,
выполнить шаг 3.
Поиск путей на графах. Обзор алгоритмов.
13

17. Эвристические алгоритмы

14
Алгоритм «лучший - первый»
• Алгоритм использует знание о пространстве поиска;
• Работает как алгоритм Дейкстры, но применяет другую тактику выбора
вершины;
• Всегда направляется к цели, но не учитывает накопленной стоимости пути.
Алгоритм «A*»
• поиск оптимального пути
• сочетает достоинства метода «лучший-первый» и метода Дейкстры;
• считается одним из лучших алгоритмов для обоих типов игровых
пространств;
Сударикова М.А. Филичев Т.А.
Поиск путей на графах. Обзор алгоритмов.
14

18. Алгоритм А*

15
Сортировка узлов по приближению наилучшего маршрута:
f(n) = g(n) + h(n)
f(n) - значение оценки, назначенное узлу n
g(n) - наименьшая стоимость достижения узла n из точки старта
h(n) - эвристическое приближение стоимости пути к цели от узла n
A* гарантированно находит кратчайший путь, до тех пор пока
эвристическое приближение h(n) является допустимым, то есть он
никогда не превышает действительного оставшегося расстояния до
цели.
Приближение обычно равняется минимальному расстоянию
между текущим узлом и целью умноженному на минимальную
стоимость передвижения между узлами. Это гарантирует
допустимость эвристики h(n)
Сударикова М.А. Филичев Т.А.
Поиск путей на графах. Обзор алгоритмов.
15

19. Алгоритм А*

16
В компьютерных играх за счет приближения стоимости пути можно
учесть дополнительные ограничения при перемещении по карте:
• Цель не обязательно должна быть единственной позицией.
Приближение тогда выбирается как минимум приближений ко всем
возможным целям
• Изменение состояний в зависимости от локальной ситуации в игре.
Для реализации поиска используются следующие основные структуры
данных.
1) представление игровой области.
2) узел или состояние поиска ( координаты, скорость объекта, g(n), h(n),
f(n), ссылка на родительский узел и т.д.)
3) Структуры хранения списков посещенных/непосещенных вершин
Структура алгоритма аналогична алгоритму Дейкстры
Ограничение: большие затраты памяти при большом числе вершин
качество сильно зависит от качества приближения h(n)
Сударикова М.А. Филичев Т.А.
Поиск путей на графах. Обзор алгоритмов.
16

20. Эксперименты(1)

17
Поиск в ширину
Серия требуемых
экспериментов проведена
на процессоре Intel серии
Core 2 Duo с тактовой
частотой 2.53 GHz
Граф ориентированный
Число ребер в графе
= ¼ максимального
числа ребер
Сударикова М.А. Филичев Т.А.
Поиск путей на графах. Обзор алгоритмов.
17

21. Эксперименты(2)

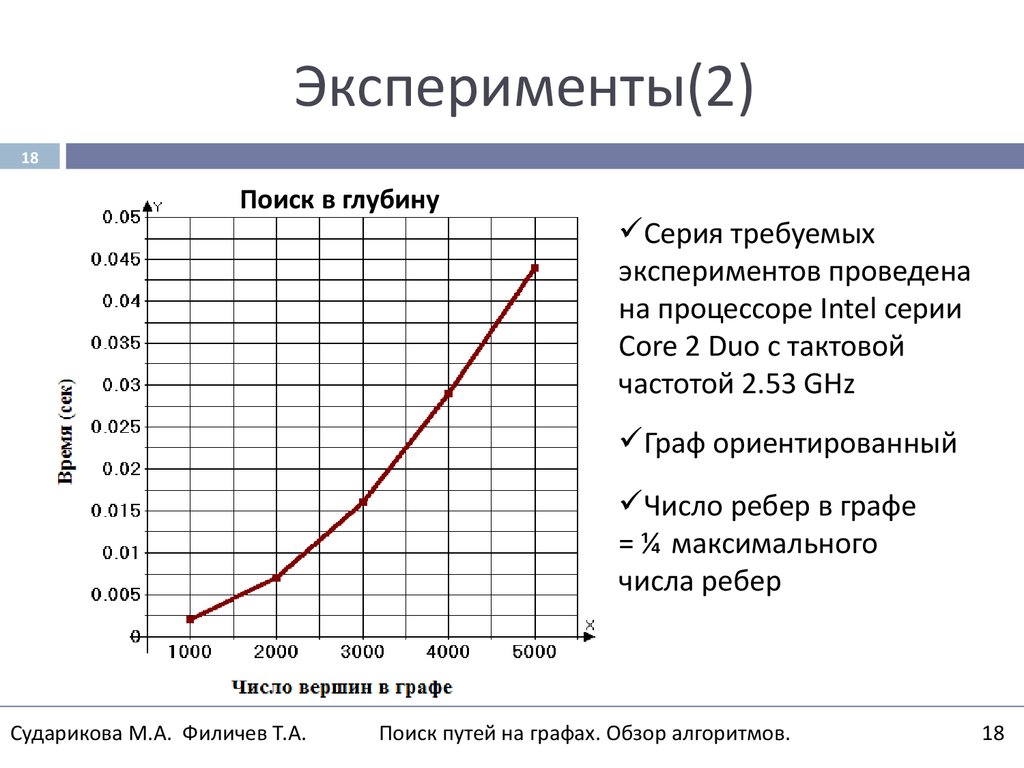
18
Поиск в глубину
Серия требуемых
экспериментов проведена
на процессоре Intel серии
Core 2 Duo с тактовой
частотой 2.53 GHz
Граф ориентированный
Число ребер в графе
= ¼ максимального
числа ребер
Сударикова М.А. Филичев Т.А.
Поиск путей на графах. Обзор алгоритмов.
18

22. Эксперименты(3)

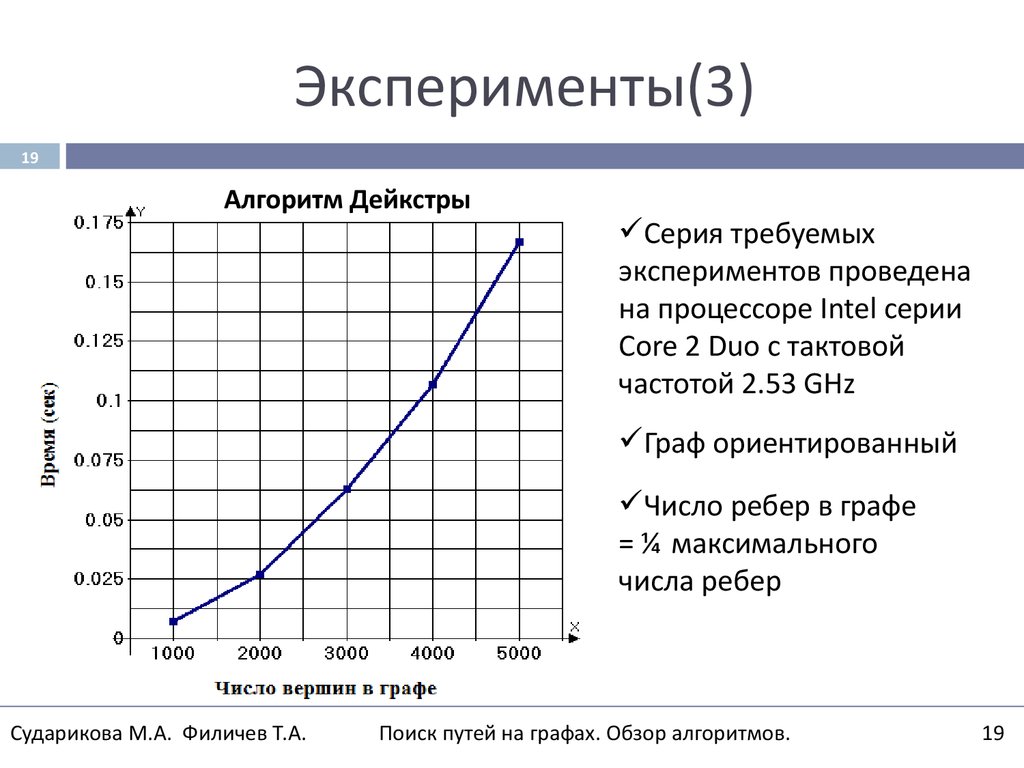
19
Алгоритм Дейкстры
Серия требуемых
экспериментов проведена
на процессоре Intel серии
Core 2 Duo с тактовой
частотой 2.53 GHz
Граф ориентированный
Число ребер в графе
= ¼ максимального
числа ребер
Сударикова М.А. Филичев Т.А.
Поиск путей на графах. Обзор алгоритмов.
19

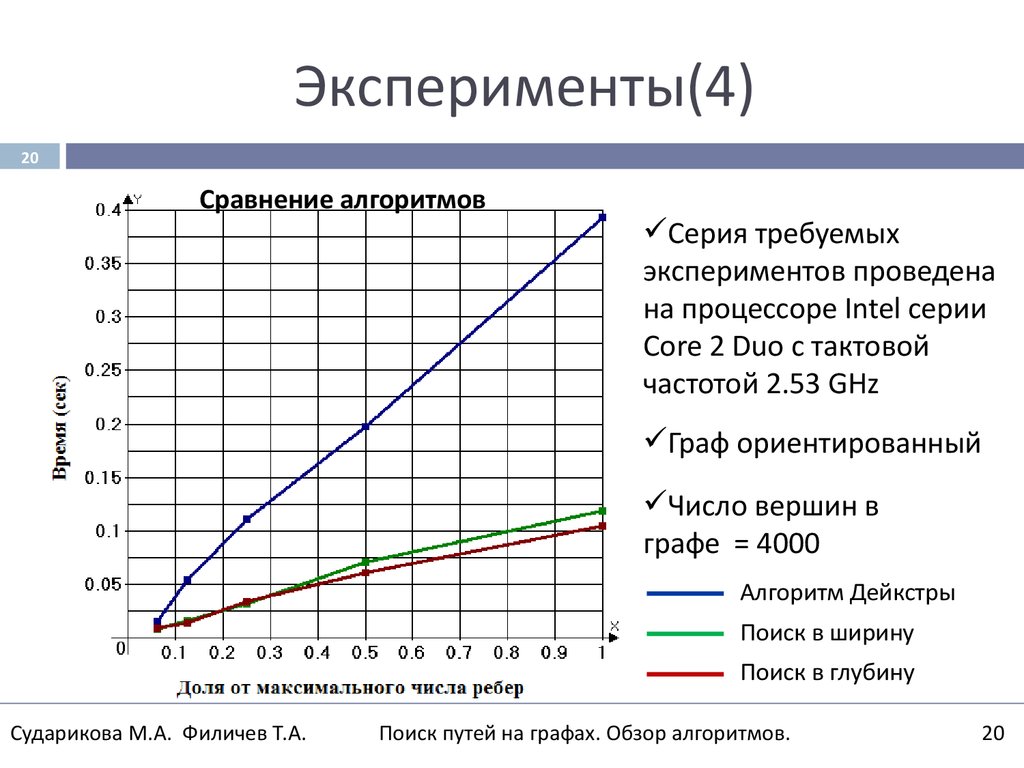
23. Эксперименты(4)

20
Сравнение алгоритмов
Серия требуемых
экспериментов проведена
на процессоре Intel серии
Core 2 Duo с тактовой
частотой 2.53 GHz
Граф ориентированный
Число вершин в
графе = 4000
Алгоритм Дейкстры
Поиск в ширину
Поиск в глубину
Сударикова М.А. Филичев Т.А.
Поиск путей на графах. Обзор алгоритмов.
20

24. Список литературы

21
1. Лекции по курсу «Теория графов», Алексеев В.Е.
2. Лекции по курсу «Анализ и разработка алгоритмов», Таланов В.А.
3. Дж. Сик, Л. Ли, Э. Ламсдэйн, С35 C++ Boost Graph Library.
Библиотека программиста / Пер. с английского Сузи Р. — СПб.:
Питер, 2006. — 304 с:
4. Материалы курса «Параллельные численные методы», Козинов
Е.А., Сиднев А.А. Кафедра математического обеспечения ЭВМ / Н.
Новгород, 243 с
5. Лекции интернет-университета. / Intuit (В.Е. Алексеев, В.А.
Таланов, Графы и алгоритмы) (http://www.intuit.ru).
6. Сайт библиотеки BOOST. / (www.boost.org).
7. Алгоритмы, методы, исходники.
(http://algolist.manual.ru/games/smartmove.php)
Сударикова М.А. Филичев Т.А.
Поиск путей на графах. Обзор алгоритмов.
21

25.

Спасибо за
внимание
Сударикова М.А. Филичев Т.А.
Поиск путей на графах. Обзор алгоритмов.
22