Похожие презентации:
Теплофизические свойства твердых тел
1. Теплофизические свойства твердых тел
zТеплофизические
свойства твердых
тел
2. Лекция 1
zЛекция 1
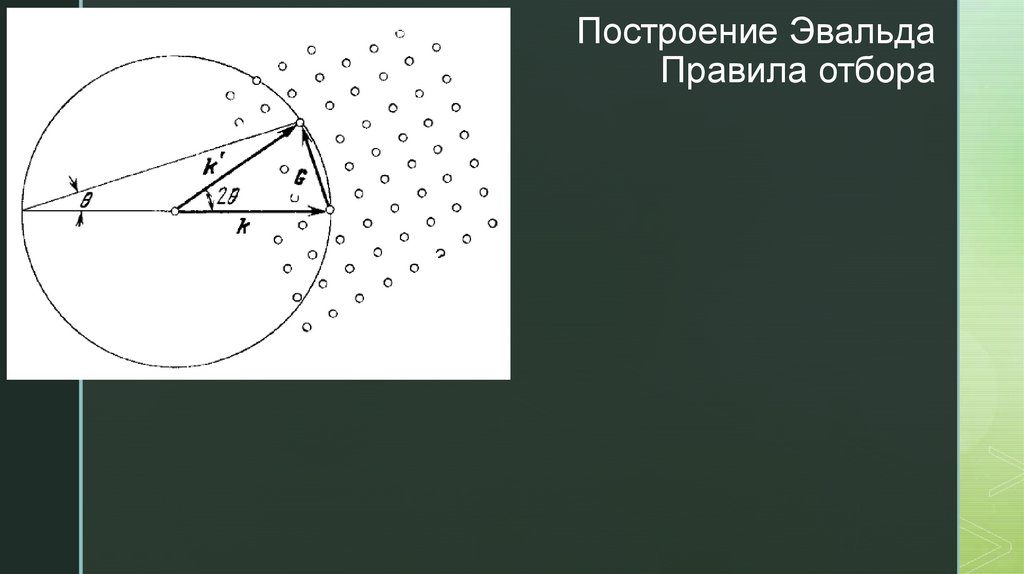
Дифракция в кристаллах.
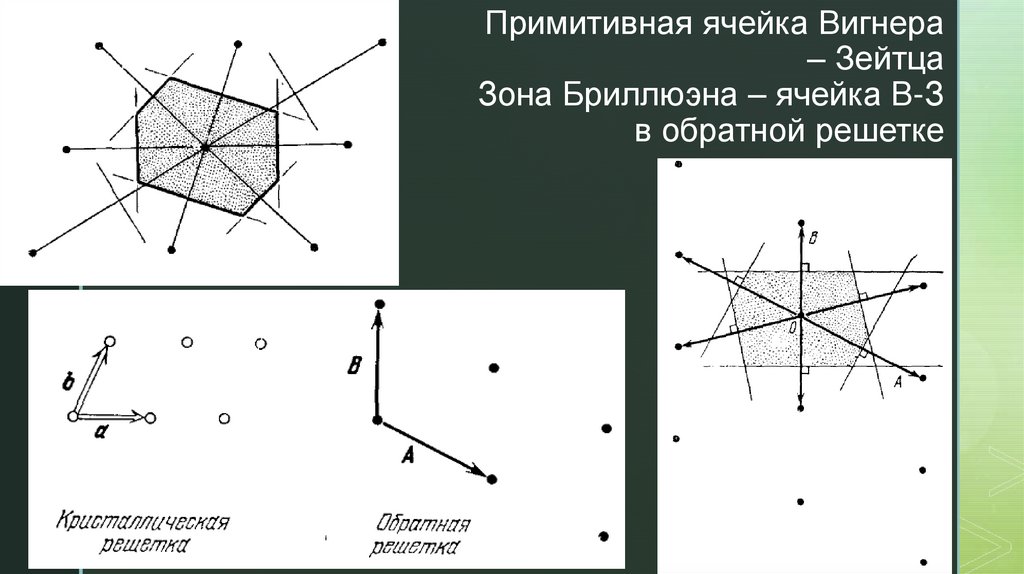
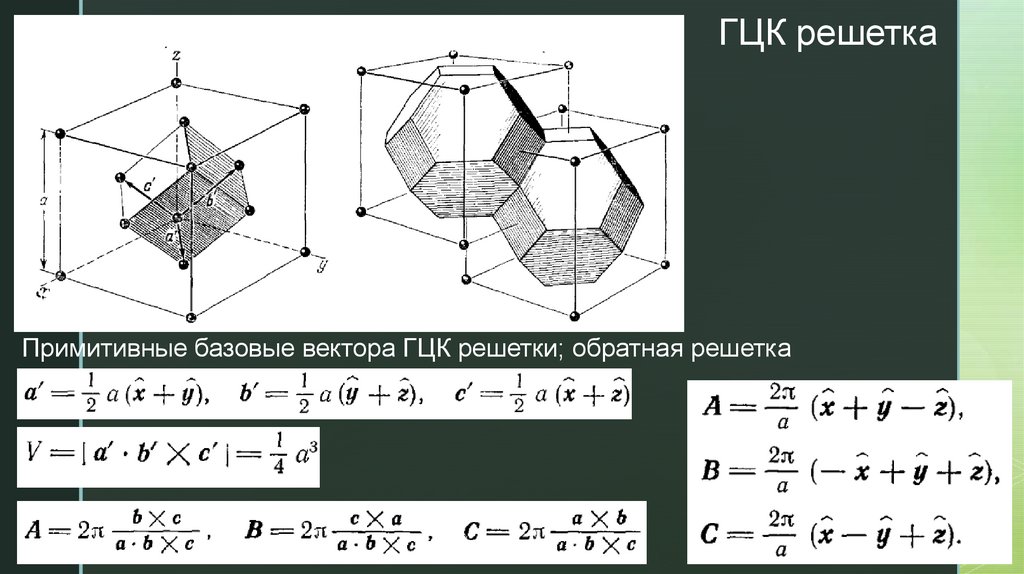
Обратная решетка.
Зоны Бриллюэна.
Форм-фактор.
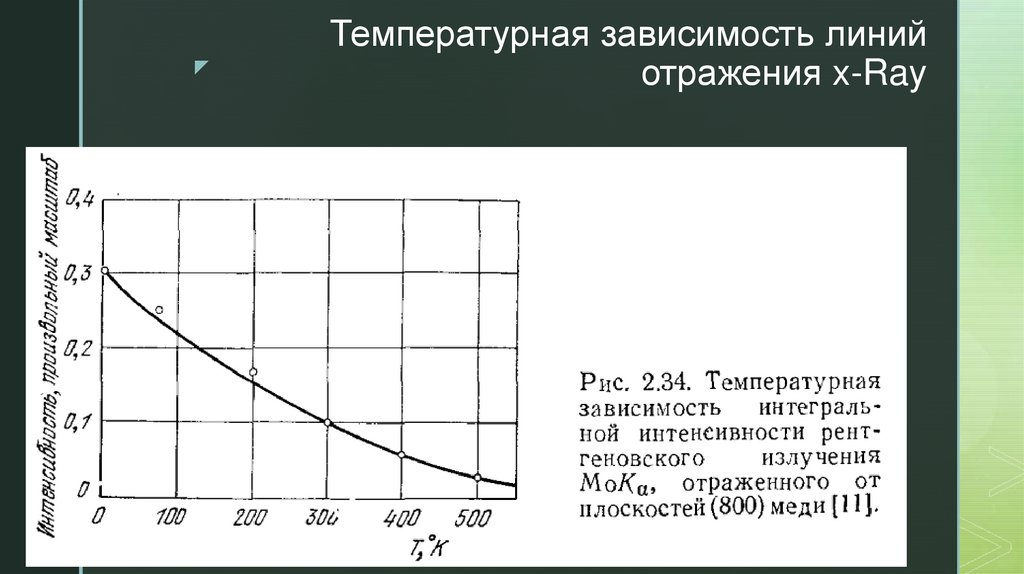
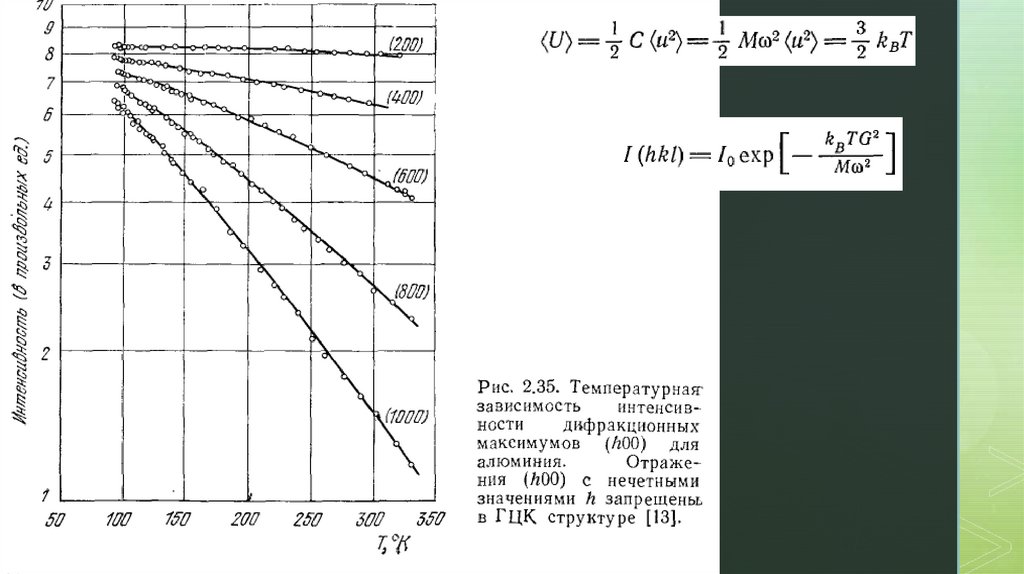
Температурная зависимость линий отражения.
3. Векторные операции: скалярное и векторное произведение
zВекторные операции: скалярное и
векторное произведение
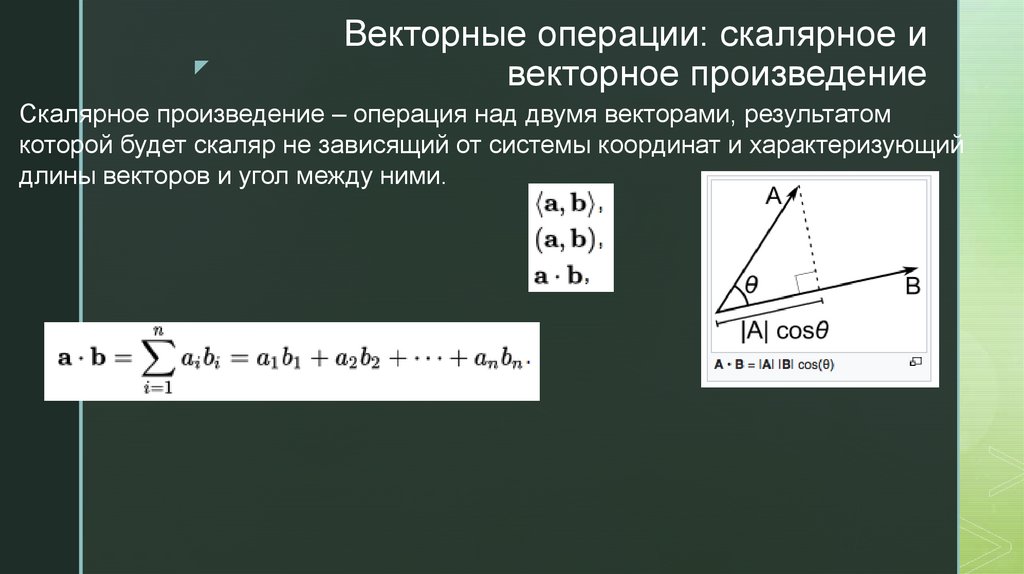
Скалярное произведение – операция над двумя векторами, результатом
которой будет скаляр не зависящий от системы координат и характеризующий
длины векторов и угол между ними.
4. Векторные операции: скалярное и векторное произведение
zВекторные операции: скалярное и
векторное произведение
5.
z6.
zeix=cos(x)+isin(x)
7.
zРотор векторного поля
дивергенция векторного поля, градиент
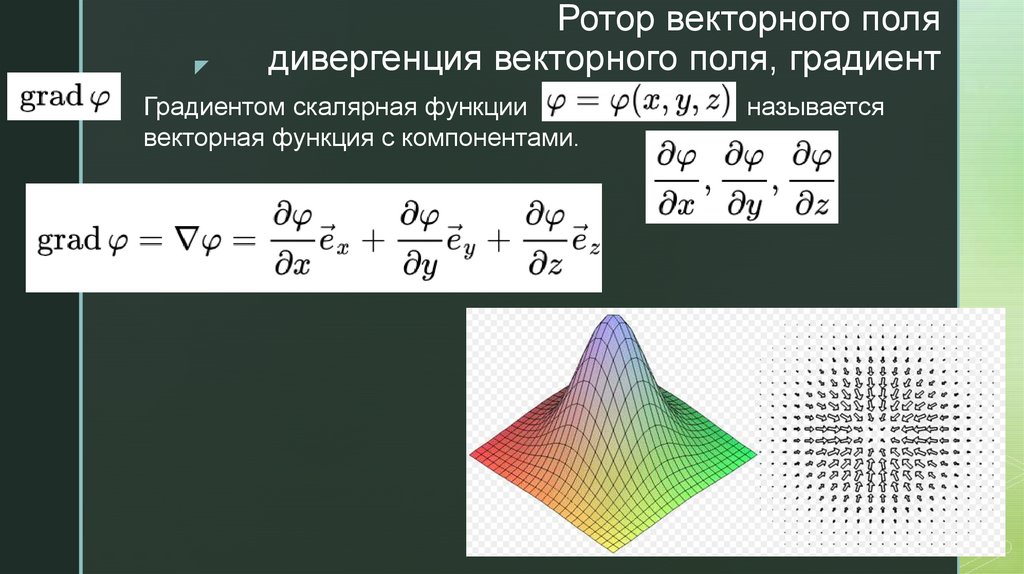
Градиентом скалярная функции
векторная функция с компонентами.
называется
8. Ротор векторного поля дивергенция векторного поля, градиент
zrot (F) =▽xF
Curl
Ротор векторного поля
дивергенция векторного поля, градиент
9.
z10.
zРотор векторного поля
дивергенция векторного поля, градиент
ФF – поток векторного поля F через сферическую поверхность площадью S,
ограничивающую объем V.
11.
z12.
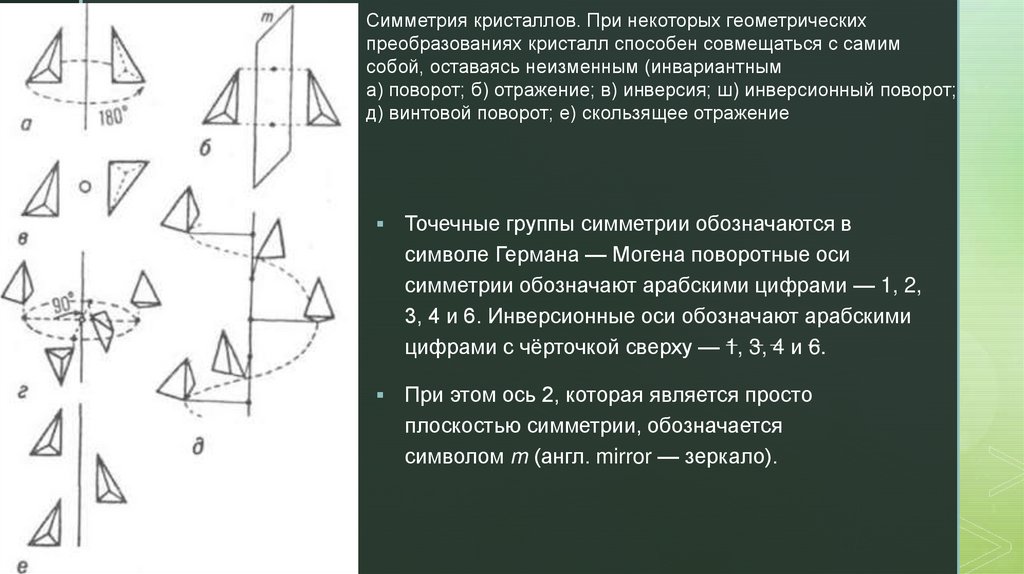
zСимметрия кристаллов. При некоторых геометрических
преобразованиях кристалл способен совмещаться с самим
собой, оставаясь неизменным (инвариантным
а) поворот; б) отражение; в) инверсия; ш) инверсионный поворот;
д) винтовой поворот; е) скользящее отражение
Точечные группы симметрии обозначаются в
символе Германа — Могена поворотные оси
симметрии обозначают арабскими цифрами — 1, 2,
3, 4 и 6. Инверсионные оси обозначают арабскими
_ __ _
цифрами с чёрточкой сверху — 1, 3, 4 и 6.
При этом ось 2, которая является просто
плоскостью симметрии, обозначается
символом m (англ. mirror — зеркало).
13.
z14.
z15.
z16.
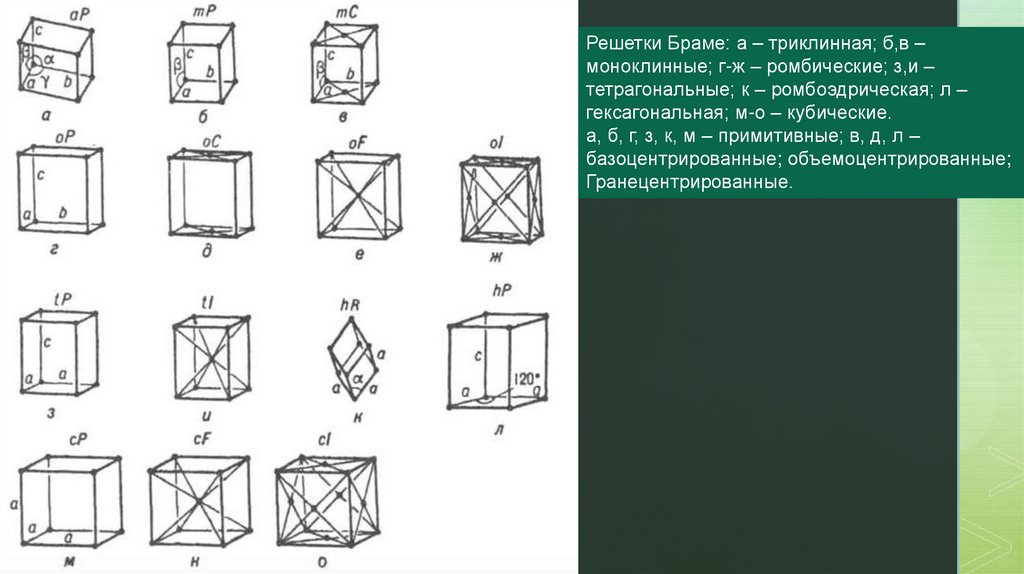
zРешетки Браме: а – триклинная; б,в –
моноклинные; г-ж – ромбические; з,и –
тетрагональные; к – ромбоэдрическая; л –
гексагональная; м-о – кубические.
а, б, г, з, к, м – примитивные; в, д, л –
базоцентрированные; объемоцентрированные;
Гранецентрированные.
17.
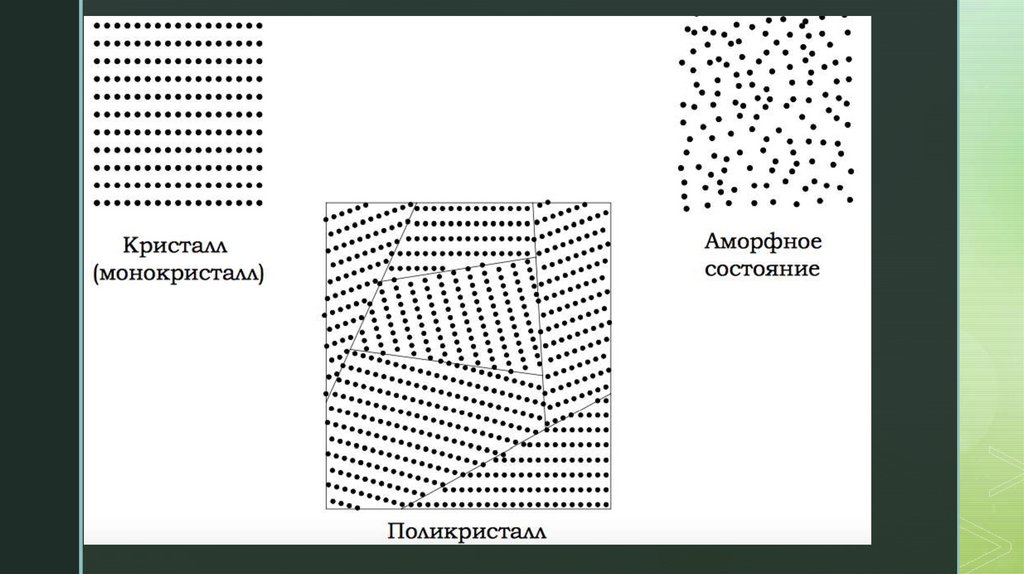
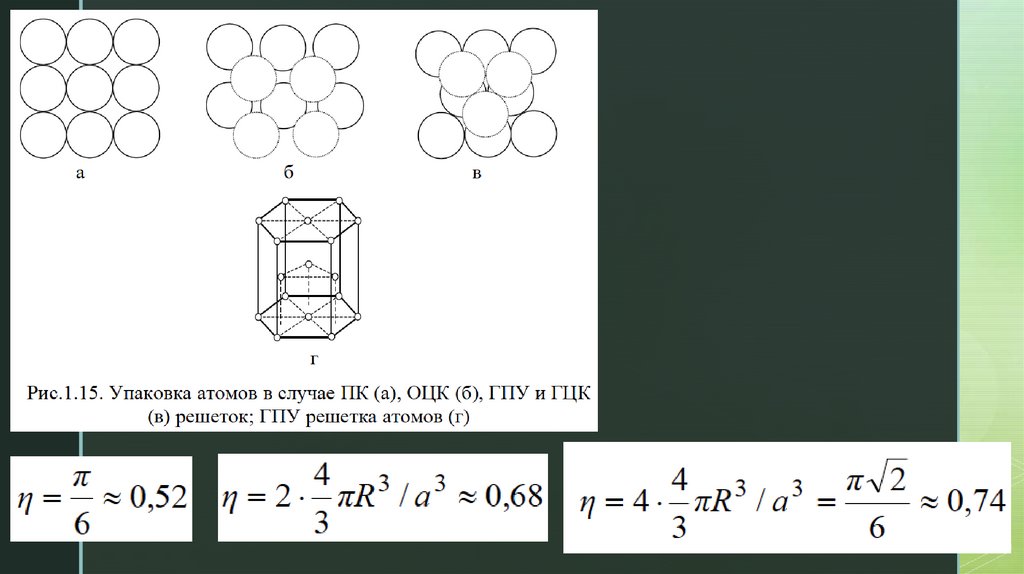
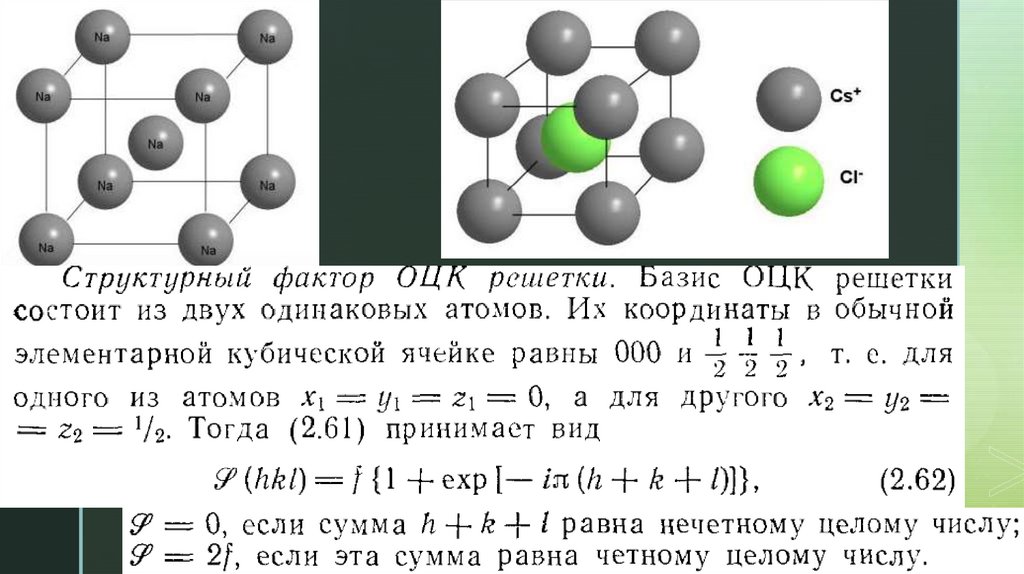
К каждой частице, находящейся в кристалле,примыкает вплотную только определенное число
соседних частиц – координационное число
z
NaCl – ГЦК
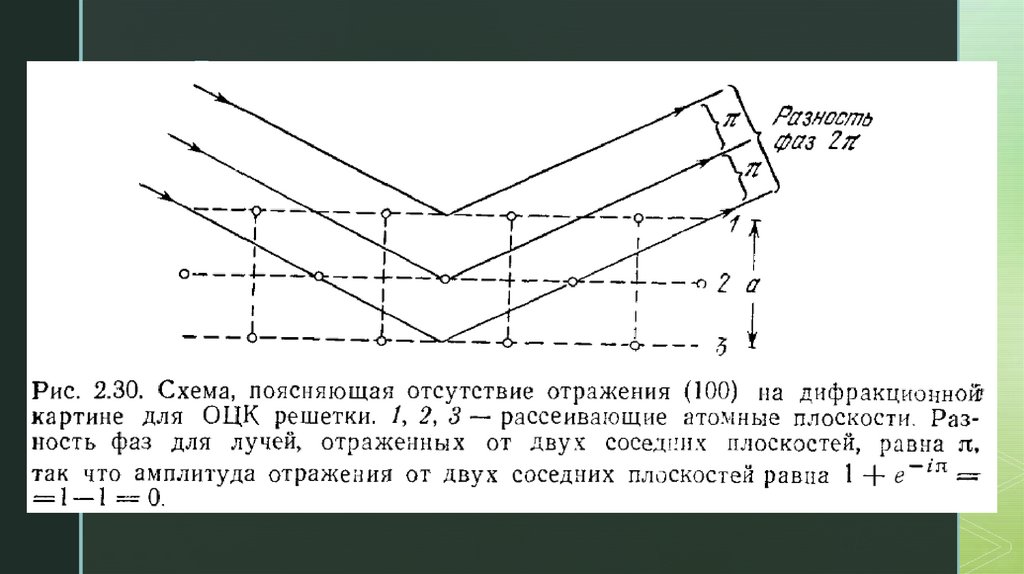
CsCl – ОЦК
Na – ?
18.
z19.
z20.
z21.
z22.
z23.
z24.
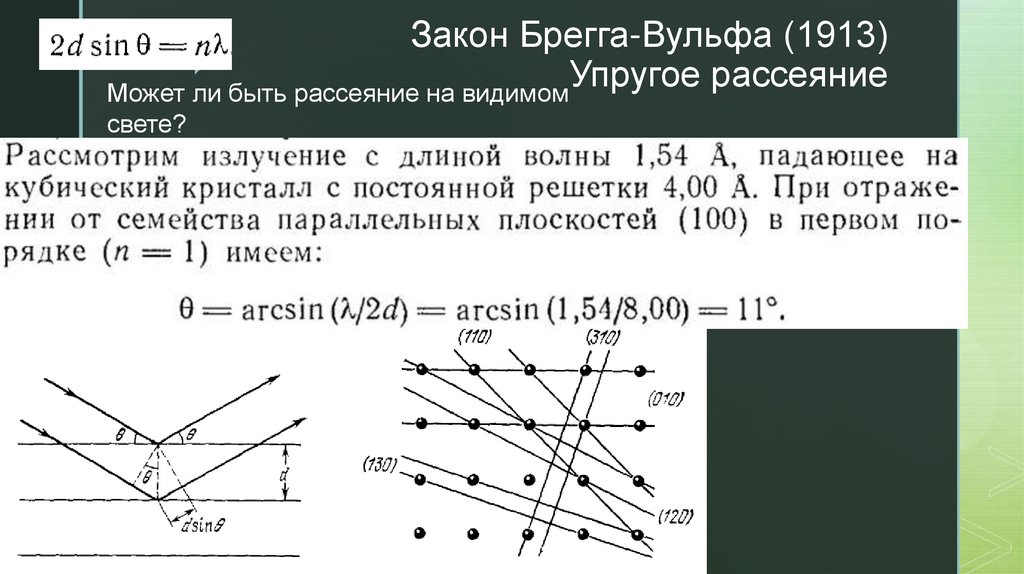
z25. Дифракция фотонов, нейтронов и электронов
zДифракция фотонов, нейтронов и
электронов
e=hf, где h – постоянная
12,4
X-Ray: l,
Планка=6.62*10-34 Дж*сек
Neutrons: длина волны де-Бройля l,
e=h2/2MNl2, где h – постоянная
Планка=6.62*10-34 Дж*сек, MN=1.675*10-24 g
l=1A при e~0.08 эВ
Electrons: длина волны де-Бройля l,
e=h2/2ml2, где h – постоянная
Планка=6.62*10-34 Дж*сек, m=0.911*10-27 g
































 Физика
Физика








