Взаимосвязь между коэффициентами корреляции и регрессии при регрессионном анализе

1. Взаимосвязь между коэффициентами корреляции и регрессии при регрессионном анализе

2. Hello!

Корреляционный анализ — это
количественный метод определения
тесноты и направления взаимосвязи
между выборочными переменными
величинами.
Регрессионный анализ — это
количественный метод определения
вида математической функции в
причинно-следственной зависимости
между переменными величинами.

3.

Зависимая переменная - та переменная, вариацию которой мы хотим
понять.
Независимые переменные - переменные, с чьей помощью мы хотим
объяснить вариацию зависимой переменной.
Дисперсия и стандартное отклонение – это способы оценки того,
насколько данные «разбросаны» вокруг среднего значения (как хорошо
среднее значение отражает характер данных)
Дисперсия показывает среднюю ошибку между ср.арифметическим и
каждым элементом выборки.
Стандартное отклонение – это квадратный корень дисперсии.
Чем меньше SD, тем лучше среднее значение отражает данные.
R2 - коэффициент детерминации, показывающий насколько хорошо
независимая переменная описывает зависимую.

4.

P-value – критерий значимости, т.е. вероятность совершить ошибку 1
рода при принятии альтернативной гипотезы.
P-value - 0,1 – 10%
Ошибка 1 рода - найти несуществующую закономерность
Ошибка 2 рода – упустить существующую закономерность

5.

Когда между двумя переменными есть связь?
“
Две переменные связаны, когда отклонение i-значения одной
переменной от среднего сопровождается отклонением от среднего
i-значения другой переменной в том же (положительная связь)
либо противоположном (отрицательная связь) направлении
Мера, которая показывает, что значения одной переменной
зависят от значений другой называется ковариация (covariance)
Слово «ковариация» означает «совместная вариация» или
«совместная дисперсия». Ковариация отражает совместную
дисперсию двух переменных.
Отсюда формула ковариации:

6.

“
Ковариация – это одна из базовых мер статистики. И
корреляция, и регрессия основаны на ковариации

7.

“
▫Если мы будем использовать ковариацию как универсальную
меру для определения степени связи значений одной переменной
с другой, мы столкнёмся с проблемой: значение ковариации
зависит от шкалы, в которой измерены переменные.
▫
Чтобы решить проблему зависимости ковариации от значений
переменных, используется процедура стандартизации
Чтобы привести ковариацию к универсальному значению, её
делят на произведение стандартных отклонений двух переменных,
для которых ковариация рассчитывается изначально:

8.

“
▫Стандартизированная ковариация является коэффициентом
корреляции Пирсона (r)
▫
Коэффициент корреляции для примера со связью между
количеством просмотров рекламных роликов определённой
фирмы-производителя ирисок и покупкой пакетов ирисок
производства этой фирмы (из Field A. et al. ... p. 206-207):

9.

“
▫Коэффициент корреляции, равняющийся 1 (+1),
означает полную положительную связь между двумя
переменным; коэффициент-1 означает полную
отрицательную связь;
▫0 – отсутствие связи.
1. Коэффициенты корреляции ничего не говорят о
наличии или отсутствии причинно-следственной
связи между переменными
2. Коэффициенты корреляции не показывают,
варьируется ли переменная x под влиянием
переменной y, и наоборот
3. Проблема третьей переменной
4. Проблема нелинейной связи

10.

“

11.

“
▫Корреляция позволяет определить, связаны ли
между собой две переменные, а также вычислить силу
связи.
Чтобы определить тип связи переменных,
используется регрессионный анализ.
▫
Регрессионный анализ показывает, какое влияние
на одну переменную оказывает одна или несколько
других переменных

12.

“
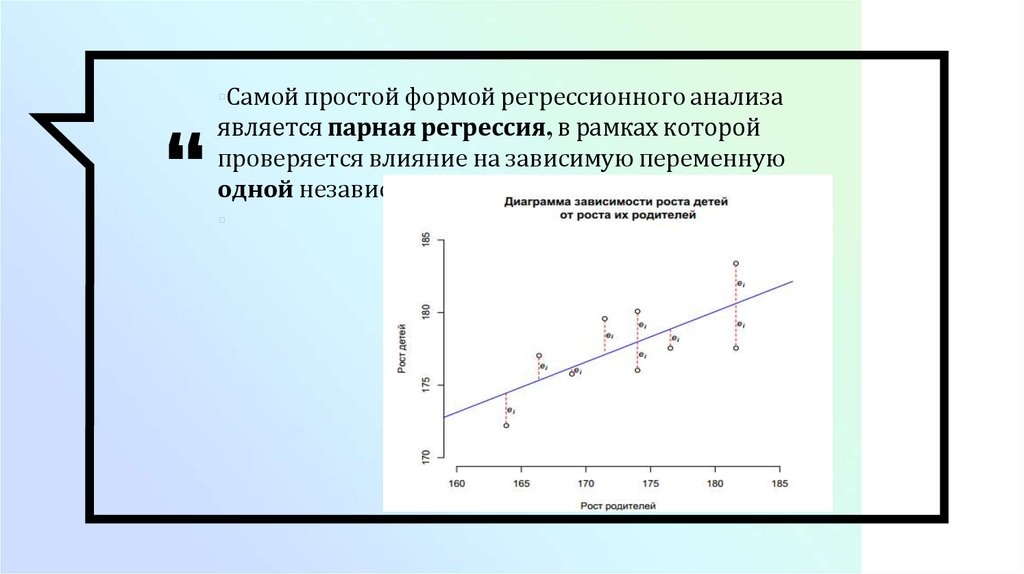
▫Самой простой формой регрессионного анализа
является парная регрессия, в рамках которой
проверяется влияние на зависимую переменную
одной независимой переменной.
▫

13.

“
▫Уравнения парной МНК-регрессии:
▫

14.

“
▫Коэффициент регрессии показывает,
насколько в среднем величина одного
признака y изменяется при изменении на
единицу меры другого, корреляционно
связанного с Y признака X.
▫Как и коэффициент корреляции, коэффициент
регрессии характеризует только линейную связь
и сопровождается знаком плюс при
положительной и знаком минус при
отрицательной связи.

15.

“
▫Формула коэффициента регрессии.
▫Rу/х = rху x (σу / σx)
где Rу/х — коэффициент регрессии;
rху — коэффициент корреляции между
признаками х и у;
(σу и σx) — среднеквадратические отклонения
признаков x и у.

16.

“
▫Уравнение регрессии - у = Му + Ry/x (х - Мx)
▫
где у — средняя величина признака, которую следует
определять при изменении средней величины другого
признака (х);
х — известная средняя величина другого признака;
Ry/x — коэффициент регрессии;
Мх, Му — известные средние величины признаков x и у.

17.

“
▫По результатам статистического исследования
физического развития мальчиков 5 лет известно, что
их средний рост (х) равен 109 см, а средняя масса тела
(у) равна 19 кг. Коэффициент корреляции между
ростом и массой тела составляет +0,9, средние
квадратические отклонения представлены в таблице.
▫Требуется рассчитать коэффициент регрессии;
▫по уравнению регрессии определить, какой будет
ожидаемая масса тела мальчиков 5 лет при росте,
равном х1 = 100 см, х2 = 110 см, х3= 120 см;

18.

“

19.

“
▫Решение.
▫Коэффициент регрессии:
Rу/х = rху х (σу / σх) = +0,9 х (0,8 / 4,4) = 0,16 кг/см.
▫Таким образом, при увеличении роста мальчиков 5 лет на 1 см
масса тела увеличивается на 0,16 кг.
▫Уравнение регрессии: у = Му + Rxy (х-Мх)
▫х1 = 100 см у1 = 19 + 0,16 (100-109) = 17,56 кг
▫х2 = 110 см у2 = 19 + 0,16 (110-109) = 19,16 кг
▫х3 = 120 см у3 = 19 + 0,16 (120-109) = 20, 76 кг

20.

“

21.

“
▫Спасибо за внимание!