Похожие презентации:
Рыночные взаимодействия в условиях несовершенной конкуренции. (Тема 4)
1. Рыночные взаимодействия в условиях несовершенной конкуренции
2. Рыночные взаимодействия в условиях несовершенной конкуренции
1. Монопольная власть2. Модели дуополии и олигополии Курно.
3. Модели дуополии и олигополии Штакельберга.
4. Модели сговора в дуополии и олигополии.
5. Модели дуополии и олигополии Бертрана.
3. 1.Монопольная власть
•Монопольнаявласть – возможность для фирмы корректировки
цены товара при изменении объема производства.
Индекс монопольной власти Лернера:
L= = –
Ed – коэффициент эластичности проса по цене
4. 1.Монопольная власть
Пусть доход R фирмы-монополиста R(y) = p(y)*y.p(y) – цена товара
y –объем производства товара
5. 1.Монопольная власть
•MR (y) = = p(y) + =p(y)*(1+ ) =
p(y)*(1+ ) = p(y)*(1+ )
Так как в условиях максимизации прибыли МR=MC, то
МС(y) = p(y)*(1+ )
Отсюда следует, что
=
6. 1.Монопольная власть
Источники монопольной власти:1) Эластичность спроса;
2) Концентрация фирм на рынке;
3) Взаимосвязь фирм на рынке.
7. 1.Монопольная власть
Индекс Хиршмана–Херфиндаля (HHI):
HHI = ,
где n – число фирм на рассматриваемом рынке;
si = yi/(y1 + … + yn), i = 1, …, n – рыночная доля i-й фирмs:
yi – объем ее выпуска,
(y1 + … + yn) – суммарный объем выпусков всех фирм, которые
действуют на рассматриваемом рынке.
8. 2.1.Модель дуополии Курно
C1 = cy1 + d1, C2 = cy2 + d2, гдеc = MC1 = MC2, d1 = FC1, d2 = FC2;
y1 – объем выпуска первой фирмы;
y2 – объем выпуска второй фирмы;
y = y1 + y2 – суммарный выпуск обеих фирм (т.е. отраслевой
выпуск);
MC1 и MC2 – предельные издержки фирм;
FC1 и FC2 – постоянные издержки обеих фирм.
9. 2.1.Модель дуополии Курно
p = a − b(y1 + y2),где a и b – положительные параметры.
R1 = py1
R2 = py2.
10. 2.1.Модель дуополии Курно
•PR1(y1, y2) = R1 − C1 = (a − by1 − by2)y1 − cy1 − d1
PR2(y1, y2) = R2 − C2 = (a − by1 − by2)y2 − cy2 − d2
Или
PR1 = (a − c)y1 – b − by1y2 − d1.
PR2 = (a − c)y2 − b− by1y2 − d2.
11. 2.1.Модель дуополии Курно
•= (a-c) -2by1 – by2 =0Отсюда
=–
Аналогично :
=–
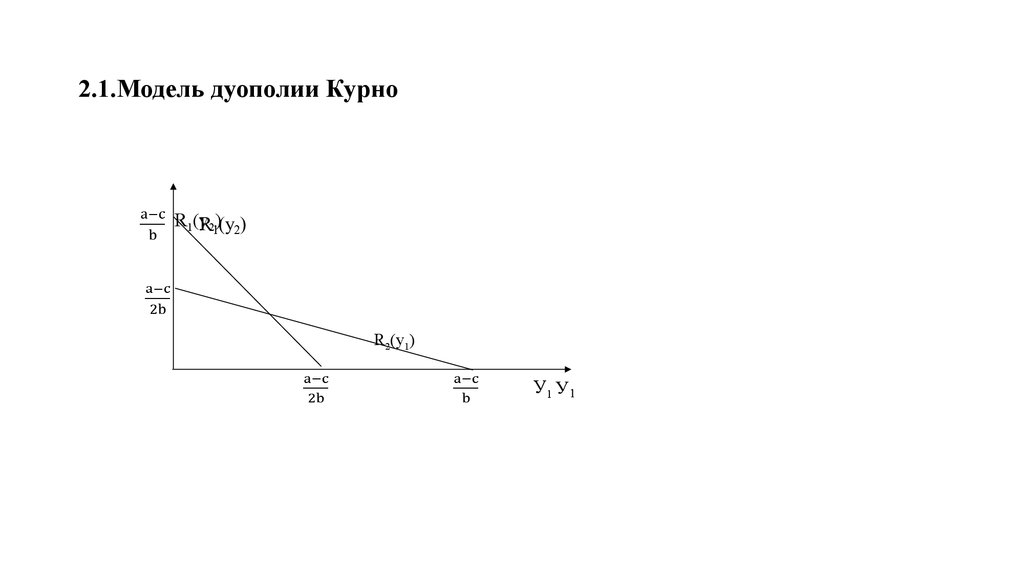
12. 2.1.Модель дуополии Курно
R1(y2)
R2(y1)
У1
13. 2.1.Модель дуополии Курно
•==
Ситуация, когда дуополисты производят товар в объемах ,
называется равновесием Курно.
14. 2.1.Модель дуополии Курно
Если• MC1 ≠ MC2, то :
PR1 = (a – c1)y1 – b − by1y2 − d1.
PR2 = (a – c2)y2 − b − by1y2 − d2.
= (a-c1) -2by1 – by2 =0
= (a-c2) -2by2 – by1 =0
Равновесие Курно достигается, когда:
=
=
15. 2.2.Модель олигополии Курно
c•i = cyi + di, i = 1, …, n,где c = MCi, di = FCi;
yi – объем выпуска фирмы Fi, i = 1, …, n;
y = y1 + … + yn – совокупный (отраслевой) выпуск.
Функция, обратная к функции рыночного спроса, имеет вид
p = a − by = a − b(y1 + … + yn), где a и b – положительные параметры.
PRi(yi) = (a − b(y1 + … + yn))yi − cyi − di, i = 1, …, n.
Или PRi(yi) = (a – с) yi – by1 yi - … - b -…- bynyi − di
16. 2.2.Модель олигополии Курно
•= (a-c) – by1 – … – 2byi –…– byn =0Отсюда = –
17. 2.2.Модель олигополии Курно
• Если все фирмы производят одинаковый объем товаров, то ихкривые реакции имеют вид:
=–
Отсюда выражаем yi и получаем объем производства каждой
фирмы в условиях равновесия Курно:
= *
18. 2.2.Модель олигополии Курно
•Пустьдоход R фирмы Fi: R(yi) = p(y)*yi.
Тогда:
= = p(y) + = p(y)*(1+ ) =
p(y)*(1+ ) = p(y)*(1+ ) = p(y)*(1+ ) = p(y)*(1+ ) = p(y)*(1+ )
19. 2.2.Модель олигополии Курно
•Таккак в условиях максимизации прибыли МR=MC, то
МСi = p(y)*(1+ )
Отсюда следует, что =
20. 2.2.Модель олигополии Курно
•Умножимобе части равенства на si и просуммируем по всем
фирмам от 1 до n:
=
Откуда:
L= = ,
где – средневзвешенные предельные издержки всех
фирм( получается делением числителя на
21. 3.1.Модель дуополии Штакельберга
Модельдуополии Штакельберга – модель асимметричной количественной дуополии.
•
Каждая из двух фирм придерживается одного из двух типов поведения:
-лидера по объему выпускаемой продукции;
- последователя.
Предпосылки модели:
1. Вторая фирма является последователем и полагает, что выпуск первой фирмы
фиксирован в производственном периоде.
2. Первая фирма является лидером и полагает, что вторая фирма сокращает в
производственном периоде объем производства в два раза, если первая фирма
увеличивает объем своего производства на одну единицу. Это формально означает,
что = – .
22. 3.1.Модель дуополии Штакельберга
•Пусть:C1 = cy1 + d1, C2 = cy2 + d2, где
p = a − b(y1 + y2), где a и b – положительные параметры.
Тогда доход (выручка) у первой фирмы равна R1 = py1, а у второй R2 = py2.
Для прибыли каждой фирмы получаем следующие выражения:
PR1(y1, y2) = R1 − C1 = (a − by1 − by2)y1 − cy1 − d1,
PR2(y1, y2) = R2 − C2 = (a − by1 − by2)y2 − cy2 − d2
Или
PR1 = (a − c)y1 – b − by1y2 − d1.
PR2 = (a − c)y2 − b− by1y2 − d2.
23. 3.1.Модель дуополии Штакельберга
•Таккак для первой фирмы = – , то
= (a-c) -2by1 – (by2 + by1) =0
Отсюда y1 = – – уравнение реакции первой фирмы.
24. 3.1.Модель дуополии Штакельберга
•Таккак для второй фирмы = 0, то
= (a–c) -2by2 – by1 =0
Отсюда y2 = – – уравнение реакции второй фирмы.
25. 3.1.Модель дуополии Штакельберга
•Подставимуравнение реакции y2 в уравнение реакции y1
y1 = – – )
Тогда =
Подставим полученное y1 в уравнение реакции y2
=
– =
При на рынке устанавливается равновесие Штакельберга.
26. 3.1.Модель дуополии Штакельберга
•ЕслиMC1 ≠ MC2, то выражения для прибыли дуополистов будут
иметь вид:
PR1 = (a – c1)y1 – b − by1y2 − d1.
PR2 = (a – c2)y2 − b − by1y2 − d2.
= (a–c) – by1 – by2 =0
= (a-c2) -2by2 – by1 =0
27. 3.1.Модель дуополии Штакельберга
•Отсюда,y1 = –
y2 = –
Равновесие Штакельберга достигается, когда:
=
=
28. 3.2.Модель олигополии Штакельберга
Предпосылки:• На рынке функционируют n фирм.
• Функция издержек фирмы-лидера С1 = с1у1+d1
• Предельные издержки фирм-последователей одинаковы и строго больше
предельных издержек фирмы-лидера.
• Каждая фирма-последователь полагает, что выпуск фирмы-лидера и других
фирм-последователей в данном производственном периоде фиксирован.
• Функция, обратная к функции рыночного спроса, имеет вид:
p = a − by = a − b(y1 + … + yn), где a и b – положительные параметры.
29. 3.2.Модель олигополии Штакельберга
Для• прибыли PRi фирм-последователей имеем представление:
PRi(yi) = (a − b(y1 + … + yn))yi − cyi − di, i = 1, …, n.
Или PRi(yi) = (a – с) yi – by1 yi – … –b –…– bynyi − di
Максимизируем прибыль:
= (a-c) – by1 – … – 2byi –…– byn =0
Отсюда = – – объем производства фирмы -последователя, который максимизирует ее
прибыль, при различных объемах производства других фирм (уравнение реакции фирмыпоследователя).
Если все фирмы-последователи производят одинаковый объем производства, то:
= –
30. 3.2.Модель олигополии Штакельберга
•Дляприбыли PR1 фирмы-лидера имеем представление:
PR1(y1) = (a − b(y1 +(n-1) yi)y1 − c1y1 – d1, i = 1, …, n.
Или PR1(y1) = (a – с) y1 –b – b(n-1)yiy1 − di
Максимизируем прибыль фирмы-лидера (с учетом = – ):
= (a – с) – 2by1 – (b(n-1)yi+ b(n-1) y1*(– ) =0
Отсюда y1 = –
31. 3.2.Модель олигополии Штакельберга
•Подставляемв уравнение y1 = –
Тогда y1 = – *
После преобразований получаем:
= +(n-1)
32. 3.2.Модель олигополии Штакельберга
•Подставляемв уравнение = –
= –
После преобразований получаем:
=–
– объемы выпуска фирмы-лидера и фирм-последователей в
условиях равновесия Штакельберга.
33. 4.Модель сговора в дуополии и олигополии
В модели сговора (модели картеля) фирмы объединяются дляпринятия решения относительно рыночной цены и общего объема
выпуска.
В этой модели все фирмы на рынке выступают как одна фирмамонополист.
34. 4.Модель сговора в дуополии и олигополии
Пусть на рынке в течение производственного периодафункционируют две фирмы.
Их функции издержек являются линейными функциями, т.е. имеют
вид C1 = cy1 + d1, C2 = cy2 + d2
Функция, обратная к функции рыночного спроса, предполагается
линейной и имеет вид p = a − by
Общая прибыль двух фирм:
PR(y) = py − C1 − C2 = (a − by)y − cy1 − d1 − cy2 − d2,
Или PR = (a − c− by)y – d1− d2
35. 4.Модель сговора в дуополии и олигополии
•= (a-c) -2by =0Отсюда y* =
В случае равного распределения объема общего выпуска по
фирмам:
y1 =y2 =
36. 4.Модель сговора в дуополии и олигополии
•В модели олигополии с n фирмами на рынке в случае равногораспределения объема общего выпуска по фирмам:
yi =
37. 4.Модель дуополии и олигополии Бертрана
Модель дуополии Бертрана представляет собой модель ценовой дуополии. Для фирмыпостоянным является не объем выпуска фирмы-конкурента, а назначаемая конкурентом цена.
Модель дуополии с однородным продуктом
Предпосылка:
• Предельные издержки фирм одинаковы.
В этих условиях потребители покупают товары той фирмы, которая предлагает меньшую
цену.
Эта модель равнозначна модели совершенной конкуренции, и равновесие Бертрана
достигается, когда цена каждой фирмы равна предельным издержкам.
Таким образом, дуополия Бертрана с однородным продуктом функционирует как рынок
совершенной конкуренции (парадокс Бертрана).
38. 4.Модель дуополии и олигополии Бертрана
Модель дуополии с дифференцированным продуктом.Пусть функции спроса на продукцию каждой фирмы имеют одни и
те же параметры и выглядят так:
y1 = h − gp1 + kp2, y2 = h − gp2 + kp1.
Все параметры h, g, k – положительные постоянные.
PR1 = p1y1 − cy1 − d1 = (p1 − c)(h − gp1 + kp2) − d1
39. 4.Модель дуополии и олигополии Бертрана
•= h − gp
1 + kp2 +(p1 − c)=0
После преобразований получаем функцию реакции R1(p2) первой
фирмы на цену p2, которую назначает вторая фирма:
p1 = p2 +
40. 4.Модель дуополии и олигополии Бертрана
• 2 = p2y2 − cy2 − d2 = (p2 − c)(h − gp1 + kp2) − d2PR
По аналогии получаем функцию реакции R2(p1) второй фирмы на
цену p1, которую назначает первая фирма:
p2 = p1 +
Решаем систему уравнений, находим равновесные и :
= =







































 Экономика
Экономика








