Похожие презентации:
Системы счисления в информатике
1. Системы счисления в информатике
Проектподготовили
Дарья Ясницкая
Григорий Чобану
Кутдусов Руслан
2. Содержание
СОДЕРЖАНИЕ1. Введение
2. История
3. Как представляются в компьютере целые числа
4. Как компьютер выполняет арифметические действия над
целыми числами
5. Система счисления
6. Способ записи чисел в позиционных системах счисления
7. Системы счисления
8. Основы машинной арифметики
9. Перевод из одной системы счисления в другую
10. Вывод
11. Источники информации
3. Введение
ВВЕДЕНИЕМы выбрали эту тему, потому что нам было
очень интересно узнать, как компьютер получает
информацию, как он производит арифметические
действия над числами. Еще нам хотелось узнать,
что такое система счисления, ее виды, как
считали в разные века, в разных странах люди.
Как переводить одну систему счисления в другую.
4. История
ИСТОРИЯСовременный человек в повседневной жизни постоянно сталкивается с
числами и цифрами. А две тысячи лет назад, что знал человек о числах? А
пять тысяч лет назад? Вопрос не простой, но очень интересный. Историки
доказали, что и пять тысяч лет тому назад люди могли записывать числа,
могли производить над ними арифметические действия. Но записывали они
числа совершенно по другим принципам, нежели мы в настоящее время. В
любом случае число изображалось с помощью одного или нескольких
символов. В математике и информатике принято символы, участвующие в
записи числа, называть цифрами. Но что же люди понимают под словом
«число»? Первоначально понятие отвлеченного числа отсутствовало, число
было «привязано» к тем предметам, которые пересчитывали. Отвлеченное
понятие натурального числа появляется вместе с развитием письменности.
Появление дробных чисел было связано с необходимостью производить
измерения . Но так как единица измерения не всегда укладывалась целое
число раз в измеряемой величине, то возникла практическая потребность
ввести более «мелкие» числа, чем натуральные.
5.
Дальнейшее развитие понятия числа было обусловлено ужеразвитием математики. Для повседневных вычислений
используется десятичная система счисления,
предшественницей которой является индусская десятичная
система, возникшая примерно в XII-м столетии. В
современной науке с развитием компьютерной техники на
первые роли выдвинулась двоичная система счисления. Ее
зачатки наблюдаются у многих народов. Например, у
древних египтян широкое распространение получили
методы умножения и деления, основанные на принципе
удвоения. Изобретение двоичного способа нумерации
приписывают китайскому императору Фо Ги, жизнь
которого относится к 4-му тысячелетию до новой эры.
Оказывается, к открытию двоичной системы счисления
имели отношение многие математики, в частности,
Фибоначчи.
6. Как представляются в компьютере целые числа
КАК ПРЕДСТАВЛЯЮТСЯ ВКОМПЬЮТЕРЕ ЦЕЛЫЕ ЧИСЛА
Целые числа могут представляться в
компьютере со знаком или без знака.
Целые числа без знака
Обычно занимают в памяти компьютера один или два байта. В
однобайтовом формате принимают значения от 000000002 до
111111112. В двухбайтовом формате — от 00000000 000000002 до
11111111 111111112.
7.
Целые числа со знакомОбычно занимают в памяти компьютера один, два или четыре байта, при
этом самый левый (старший) разряд содержит информацию о знаке числа.
Диапазоны значений целых чисел со знаком
8.
Рассмотрим особенности записи целых чисел со знаком на примереоднобайтового формата, при котором для знака отводится один
разряд, а для цифр абсолютной величины — семь разрядов.
Последние две формы применяются особенно широко, так как
позволяют упростить конструкцию арифметико-логического
устройства компьютера путем замены разнообразных
арифметических операций операцией сложения.
Положительные числа в прямом, обратном и дополнительном
кодах изображаются одинаково - двоичными кодами с цифрой 0 в
знаковом разряде.
Отрицательные числа в прямом, обратном и дополнительном
кодах имеют разное изображение.
9. Как компьютер выполняет арифметические действия над целыми числами
КАК КОМПЬЮТЕР ВЫПОЛНЯЕТАРИФМЕТИЧЕСКИЕ ДЕЙСТВИЯ
НАД ЦЕЛЫМИ ЧИСЛАМИ
Сложение и вычитание
В большинстве компьютеров операция вычитания не
используется. Вместо нее производится сложение
обратных или дополнительных кодов уменьшаемого и
вычитаемого. Это позволяет существенно упростить
конструкцию АЛУ.
10.
На преобразование отрицательного числа в обратный кодкомпьютер затрачивает меньше времени, чем на
преобразование в дополнительный код, так как последнее
состоит из двух шагов — образования обратного кода и
прибавления единицы к его младшему разряду;
время выполнения сложения для дополнительных кодов чисел
меньше, чем для их обратных кодов, потому что в таком
сложении нет переноса единицы из знакового разряда в
младший разряд результата.
Умножение и деление
Во многих компьютерах умножение производится как последовательность
сложений и сдвигов. Для этого в АЛУ имеется регистр, называемый
накапливающим сумматором, который до начала выполнения операции
содержит число ноль. В процессе выполнения операции в нем поочередно
размещаются множимое и результаты промежуточных сложений, а по
завершении операции — окончательный результат.
Другой регистр АЛУ, участвующий в выполнении этой операции, вначале
содержит множитель. Затем по мере выполнения сложений
содержащееся в нем число уменьшается, пока не достигнет нулевого
значения.
11.
Для иллюстрации умножим 1100112 на 1011012 .Деление для компьютера является трудной операцией.
Обычно оно реализуется путем многократного прибавления
к делимому дополнительного кода делителя.
12. Система счисления
СИСТЕМА СЧИСЛЕНИЯСистема счисления — это способ записи чисел с помощью
заданного набора специальных знаков (цифр).
Существуют системы позиционные и непозиционные.
В непозиционных системах счисления вес цифры не зависит
от позиции, которую она занимает в числе. Так, например, в
римской системе счисления в числе XXXII (тридцать два)
вес цифры X в любой позиции равен просто десяти.
В позиционных системах счисления вес каждой цифры
изменяется в зависимости от ее позиции в
последовательности цифр, изображающих число. Любая
позиционная система характеризуется своим основанием.
Основание позиционной системы счисления — это
количество различных знаков или символов, используемых для
изображения цифр в данной системе. За основание можно
принять любое натуральное число — два, три, четыре,
шестнадцать и т.д. Следовательно, возможно бесконечное
множество позиционных систем.
13.
Десятичная система счисления:Пришла в Европу из Индии, где она появилась не позднее VI века н.э. В этой системе 10 цифр: 0,
1, 2, 3, 4, 5, 6, 7, 8, 9, но информацию несет не только цифра, но и место, на котором цифра
стоит (то есть ее позиция). В десятичной системе счисления особую роль играют число 10 —
основание системы, и его степени: 10, 100, 1000 и т.д. Самая правая цифра числа показывает
число единиц, вторая справа — число десятков, следующая — число сотен и т.д.
Двоичная система счисления:
В этой системе всего две цифры — 0 и 1. Особую роль здесь играет число 2 и его степени: 2, 4,
8 и т.д. Самая правая цифра числа показывает число единиц, следующая цифра — число двоек,
следующая — число четверок и т.д. Двоичная система счисления позволяет закодировать
любое натуральное число — представить его в виде последовательности нулей и единиц. В
двоичном виде можно представлять не только числа, но и любую другую информацию: тексты,
картинки, фильмы и аудиозаписи. Инженеров двоичное кодирование привлекает тем, что легко
реализуется технически. Например, при подаче сигнала тока возможны 2 случая — есть сигнал
(1) и нет сигнала (0).
Восьмеричная система счисления:
В этой системе счисления 8 цифр: 0, 1, 2, 3, 4, 5, 6, 7. Цифра 1, указанная в самом младшем
разряде, означает — как и в десятичном числе — просто единицу. Та же цифра 1 в следующем
разряде означает 8, в следующем 64 и т.д. Число 100 (восьмеричное) есть не что иное, как 64
(десятичное).
Шестнадцатеричная система счисления:
Запись числа в восьмеричной системе счисления достаточно компактна, но еще компактнее
она получается в шестнадцатеричной системе. В качестве первых 10 из 16
шестнадцатеричных цифр взяты привычные цифры 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, а вот в качестве
остальных 6 цифр используют первые буквы латинского алфавита: A, B, C, D, E, F. Цифра 1,
записанная в самом младшем разряде, означат просто единицу. Та же цифра 1 в следующем —
16 (десятичное), в следующем — 256 (десятичное) и т.д. Цифра F, указанная в самом младшем
разряде, означает 15 (десятичное).
14. Способ записи чисел в позиционных системах счисления
СПОСОБ ЗАПИСИ ЧИСЕЛ ВПОЗИЦИОННЫХ СИСТЕМАХ
СЧИСЛЕНИЯ
В каждой системе счисления цифры упорядочены в соответствии с их
значениями: 1 больше 0, 2 больше 1 и таким образом мы продвигаемся от
одного числа к другому.
Основание позиционной системы счисления — это количество различных
знаков или символов, используемых для изображения цифр в данной
системе.
За основание можно принять любое натуральное число, начиная с двойки
— два, три, четыре, шестнадцать и т.д. Следовательно, возможно
бесконечное множество позиционных систем.
Позиционной системы счисления с основанием 1 быть не может.
Продвижением цифры называют замену ее следующей по величине.
Продвинуть цифру 1 — значит заменить ее на 2, продвинуть цифру 2 —
значит заменить ее на 3 и т.д. Но в позиционной системе счисления
цифр ограниченное количество, как же продвинуть старшую цифру
(например 9 в десятичной системе счисления)?
Продвижение старшей цифры означает замену ее на 0.
15.
Целые числа в любой системе счисления порождаются поправилу счета:
для образования целого числа, следующего за любым данным целым
числом, нужно продвинуть самую правую цифру числа(в младшем
разряде); если после продвижения какая-либо цифра стала нулем, то
нужно продвинуть цифру, стоящую слева от нее (по умолчанию
слева 0).
Сейчас в большинстве стран мира, несмотря на то, что там
говорят на разных языках, считают одинаково, «по-арабски». Но
так было не всегда. Еще каких-то пятьсот лет назад ничего
подобного и в помине не было даже в просвещенной Европе, не
говоря уже о какой-нибудь Африке или Америке.
Но тем не менее числа люди все равно как-то записывали. У
каждого народа была своя собственная или позаимствованная у
соседа система записи чисел. Одни использовали буковки, другие —
значки, третьи — закорючки. У кого-то получалось удобнее, у когото не очень.
Ведь не так-то просто даже имея цифры (значки, которыми
записываются числа), записать какое-нибудь число. Для этого
нужна система счисления (способ записи чисел с помощью цифр).
(Сразу хочу предупредить, что системы счисления бывают
непозиционными и позиционными или аддитивными и
мультипликативными).
16. Системы счисления
СИСТЕМЫ СЧИСЛЕНИЯСистема счисления — очень сложное понятие. Оно включает
в себя все законы, по которым числа записываются и
читаются, а так же те, по которым производятся операции
над ними.
Самое главное, что нужно знать о системе счисления — ее
тип: аддитивная или мультипликативная. В первом типе
каждая цифра имеет свое значение, и для прочтения числа
нужно сложить все значения использованных цифр:
XXXV = 10+10+10+5 = 35; CCXIX = 100+100+10-1+10 = 219;
Во втором типе каждая цифра может иметь разные
значения в зависимости от своего местоположения в числе:
(иероглифы по порядку: 2, 1000, 4, 100, 2, 10, 5)Здесь дважды
использован иероглиф «2″, и в каждом случае он принимал
разные значения «2000″ и «20″.
17.
Для аддитивной системы нужно знать все цифры-символы с ихзначениями (их бывает до 4 — 5 десятков), и порядок записи.
Например, в Латинской записи если меньшая цифра записана перед
большей, то производится вычитание, а если после, то сложение (IV =
(5-1) = 4; VI = (5+1) = 6).
Для мультипликативной системы нужно знать изображение цифр и
их значение, а так же основание системы счисления. Определить
основание очень легко, нужно только пересчитать количество
значащих цифр в системе. Если проще, то это число, с которого
начинается второй разряд у числа. Мы, например, используем цифры 0,
1, 2, 3, 4, 5, 6, 7, 8, 9. Их ровно 10, поэтому основание нашей системы
счисления тоже 10, и система счисления называется «десятичная». В
вышеприведенном примере используются цифры 0, 1, 2, 3, 4, 5, 6, 7, 8, 9
(вспомогательные 10, 100, 1000, 10000 и т. д. не в счет). Основных
цифр здесь тоже 10, и система счисления — десятичная.
Как можно догадаться, сколько есть чисел, столько же может быть
и оснований систем счисления. Но используются только самые
удобные основания систем счисления.
18.
Аддитивные системы счисленияВ этой системе счисления для записи чисел используется уже не одна, а
несколько цифр. Они могут изображаться так, как взбредет в голову, но
только разные цифры должны выглядеть по-разному. Такая система
счисления уже годится для записи чисел, но она крайне неудобна для счета.
акой системой счисления пользовались Египтяне, Ацтеки, племена Майя.
Мультипликативные системы счисления
В таких системах счисления для записи чисел используется уже
определенное количество цифр, которые могут принимать разные значения
в зависимости от расположения в записи числа. Все цифры здесь
изображаются определенными символами.
Например 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10 11, 12, …, 99, 100, 101 …
Такие системы счисления были только у народов с очень хорошо развитой
математикой. По сей день мы используем только такую систему
счисления.
Такая система счисления годится для записи чисел, и она очень удобна для
счета. Любое из действий арифметики и алгебры может быть выполнено
легко. Для счета здесь не нужна большая сноровка.
19.
Посмотрите, как записывали цифры у разных народов вглубокой древности:
20. Основы машинной арифметики
ОСНОВЫ МАШИННОЙАРИФМЕТИКИ
В позиционной системе счисления любое число записывается в виде
последовательности цифр:
A( S ) = a n S N + an – 1 Sn — 1 + a1 S1 + a0 S0
Основание позиционной системы счисления определяет ее
название. В вычислительной технике применяются двоичная,
восьмеричная, десятичная и шестнадцатеричная системы. В
дальнейшем, чтобы явно указать используемую систему счисления,
будем заключать число в скобки и в индексе указывать основание
системы счисления.
В двоичной системе счисления используются только две цифры: 0
и 1. Любое двоичное число может быть представлено в следующей
форме:
A2= +(am-1 2m-1)+a m-2 2m-2+…+a 0+a-1 2 -1+…+a–l 2-l)
В восьмеричной системе счисления для записи чисел используется
восемь цифр (0,1,2,3,4,5,6,7), а в шестнадцатеричной —
шестнадцать (0,1,2,3,4,5,6,7,8,9,A,B,C,D,E,F).
21.
Для хранения и обработки данных в ЭВМ используетсядвоичная система, так как она требует наименьшего
количества аппаратуры по сравнению с другими системами.
Все остальные системы счисления применяются только для
удобства пользователей.
В двоичной системе очень просто выполняются
арифметические и логические операции над числами.
Много разрядные числа складываются, вычитаются,
умножаются и делятся по тем же правилам, что и в
десятичной системе счисления.
22. Перевод из одной системы счисления в другую
ПЕРЕВОД ИЗ ОДНОЙСИСТЕМЫ СЧИСЛЕНИЯ В
ДРУГУЮ
Перевод числа из одной системы в другую выполняется по универсальному
алгоритму, заключающемуся в последовательном делении целой части
числа и образующихся целых частных на основание новой системы
счисления, записанное в исходной системе счисления, и в последующем
умножении дробной части и дробных частей получающихся произведений
на то же основание, записанное в исходной системе счисления.
При переводе целой части получающиеся в процессе последовательного
деления остатки представляют цифры целой части числа в новой
системе счисления, записанные цифрами исходной системы счисления.
Последний остаток является старшей цифрой переведенного числа.
23.
При переводе дробной части числа целые части чисел, получающихсяпри умножении, не участвуют в последующих умножениях. Они
представляют собой цифры дробной части исходного числа в новой
системе счисления, изображенные числами старой системы. Значение
первой целой части является первой цифрой после запятой
переведенного числа.
Если при переводе дробной части получается периодическая дробь, то
производят округление, руководствуясь заданной точностью
вычислений.
При переводе чисел из любой системы счисления в десятичную удобнее
пользоваться непосредственно формулой ( II ): (775)8 = 7*8(2) + 7*8 + 5
= (509)10
Для осуществления автоматического перевода десятичных чисел в
двоичную систему счисления необходимо вначале каким-то образом
ввести их в машину, Для этой цели обычно используется двоичнодесятичная запись чисел или представление этих чисел в кодах ASCII.
При двоично-десятичной записи каждая цифра десятичного числа
заменяется четырехзначным двоичным числом (тетрадой):
(983,65)10 = (1001 1000 0011, 0110 0101)2-10
24.
При записи чисел в кодах ASCII цифрам от 0 до 9 поставлены всоответствие восьмиразрядные двоичные коды от 00110000 до
00111001.
ЭВМ, предназначенные для обработки экономической информации,
например IBM AT, позволяют производить арифметические
операции в десятичной системе счисления над числами,
представленными в двоично-десятичных кодах и кодах ASCII.
Шестнадцатеричная и восьмеричная системы счисления
используются только программистами и операторами ЭВМ, так
как представление чисел в этих системах более компактное, чем в
двоичной, и перевод из этих систем в двоичную и обратно
выполняется очень просто (основания этих систем представляют
собой целую степень числа 2).
Для перевода восьмеричного числа в двоичное достаточно каждый
восьмеричный разряд представить тремя двоичными (триадой), а
для перевода шестнадцатеричного числа — четырьмя (тетрадой).
25.
Перевод из десятичной системы счисления в двоичную,восьмеричную и шестнадцатеричную:
а) исходное целое число делится на основание системы
счисления, в которую переводится (на 2 — при переводе в
двоичную систему счисления или на 16 — при переводе в
шестнадцатеричную); получается частное и остаток;
б) если полученное частное меньше основания системы
счисления, в которую выполняется перевод, процесс деления
прекращается, переходят к шагу в). Иначе над частным
выполняют действия, описанные в шаге а);
в) все полученные остатки и последнее частное
преобразуются в соответствии с таблицей перевода в
цифры той системы счисления, в которую выполняется
перевод;
г) формируется результирующее число: его старший разряд
– полученное последнее частное, каждый последующий
младший разряд образуется из полученных остатков от
деления, начиная с последнего и кончая первым. Таким
образом, младший разряд полученного числа – первый
остаток от деления, а старший – последнее частное.
26.
Выполняем перевод числа 19 в двоичную системусчисления:
Перевод из двоичной, восьмеричной и
шестнадцатеричной систем счисления в десятичную:
Выполним перевод числа 1316 в десятичную систему
счисления.
Имеем:
1316 = 1*161 + 3*160 = 16 + 3 = 1910.
Таким образом, 1316 = 1910.
27.
Перевод из двоичной системы счисления вшестнадцатеричную:
а) исходное число разбивается на тетрады (т.е. 4 цифры), начиная с
младших разрядов. Если количество цифр исходного двоичного числа не
кратно 4, оно дополняется слева незначащими нулями до достижения
кратности 4;
б) каждая тетрада заменятся соответствующей
шестнадцатеричной цифрой в соответствии с таблицей.
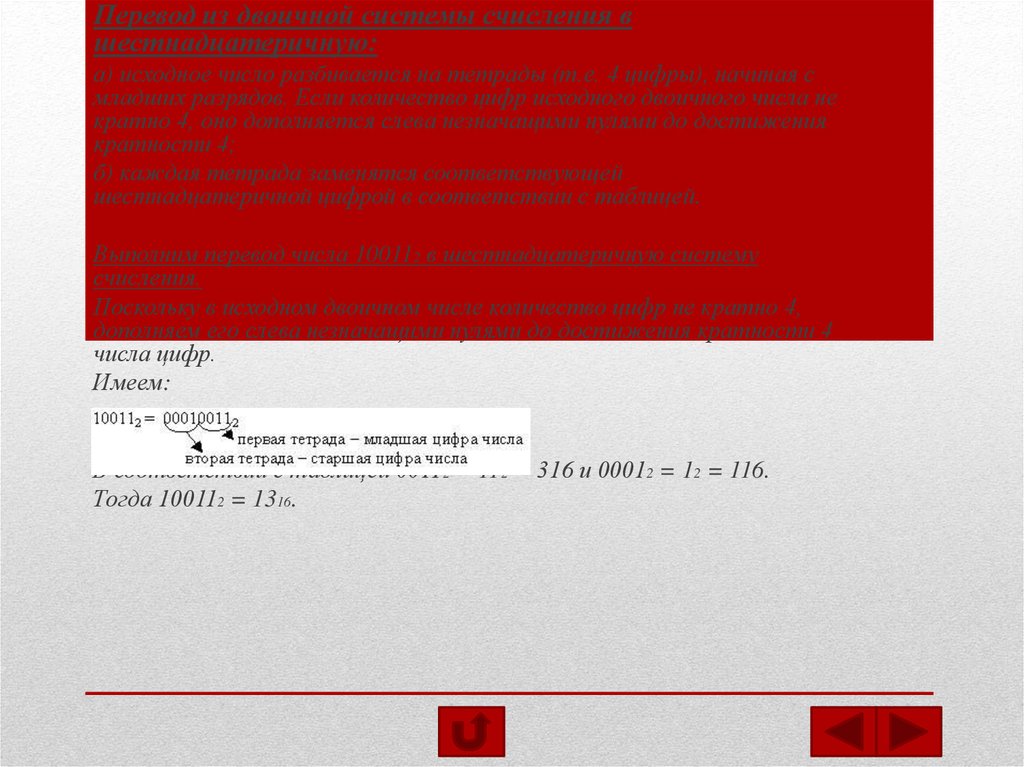
Выполним перевод числа 100112 в шестнадцатеричную систему
счисления.
Поскольку в исходном двоичном числе количество цифр не кратно 4,
дополняем его слева незначащими нулями до достижения кратности 4
числа цифр.
Имеем:
В соответствии с таблицей 00112 = 112 = 316 и 00012 = 12 = 116.
Тогда 100112 = 1316.
28.
Перевод из шестнадцатеричной системы счисления вдвоичную:
а) каждая цифра исходного числа заменяется тетрадой
двоичных цифр в соответствии с таблицей. Если в таблице
двоичное число имеет менее 4 цифр, оно дополняется слева
незначащими нулями до тетрады;
б) незначащие нули в результирующем числе
отбрасываются.
Выполнить перевод числа 1316 в двоичную систему
счисления.
По таблице имеем:
116 = 12 и после дополнения незначащими нулями двоичного
числа 12 = 00012;
316 = 112 и после дополнения незначащими нулями двоичного
числа 112 = 00112.
Тогда 1316 = 000100112. После удаления незначащих нулей
имеем 1316 = 100112.
29.
Перевод из двоичной системы счисления в восьмеричную ишестнадцатеричную:
Таблица соответствия восьмеричных цифр и двоичного кода
30.
Чтобы перевести число из двоичной системы ввосьмеричную или шестнадцатеричную, его нужно разбить
влево и вправо от запятой на триады (для восьмеричной)
или тетрады (для шестнадцатеричной) и каждую такую
группу заменить соответствующей восьмеричной
(шестнадцатеричной) цифрой.
31. Вывод
ВЫВОДПодводя итоги работы, мы определили для себя следующие выводы.
Позиционная система счисления состоит в использовании ограниченного числа
цифр, зато позиция каждой цифры в числе обеспечивает значимость (вес) этой
цифры. Позиция цифры в числе на математическом языке называется разрядом.
Основание позиционной системы счисления - это количество различных знаков или
символов (цифр), используемых для отображения чисел в данной системе.
Для того чтобы двоичные числа, отличающиеся довольно значительной длиной,
было легче воспринимать и отображать, их сжимают в восьмеричную и
шестнадцатеричную системы счисления.
В компьютерных технологиях все виды информации кодируются только цифрами
или, точнее, числами, которые представляются в двоичной системе счисления способе представления любых чисел с помощью двух знаков (цифр) по
позиционному принципу.
32. Источники информации
ИСТОЧНИКИ ИНФОРМАЦИИИнтернет ресурсы:
http://garnett.ru/10-klass/proekt-po-teme-sistemy-schisleniia/
http://refoteka.ru/r-171100.html
https://yandex.ru/images/































 Информатика
Информатика








