Похожие презентации:
Теоретические основы бокового каротажа
1. Теоретические основы бокового каротажа
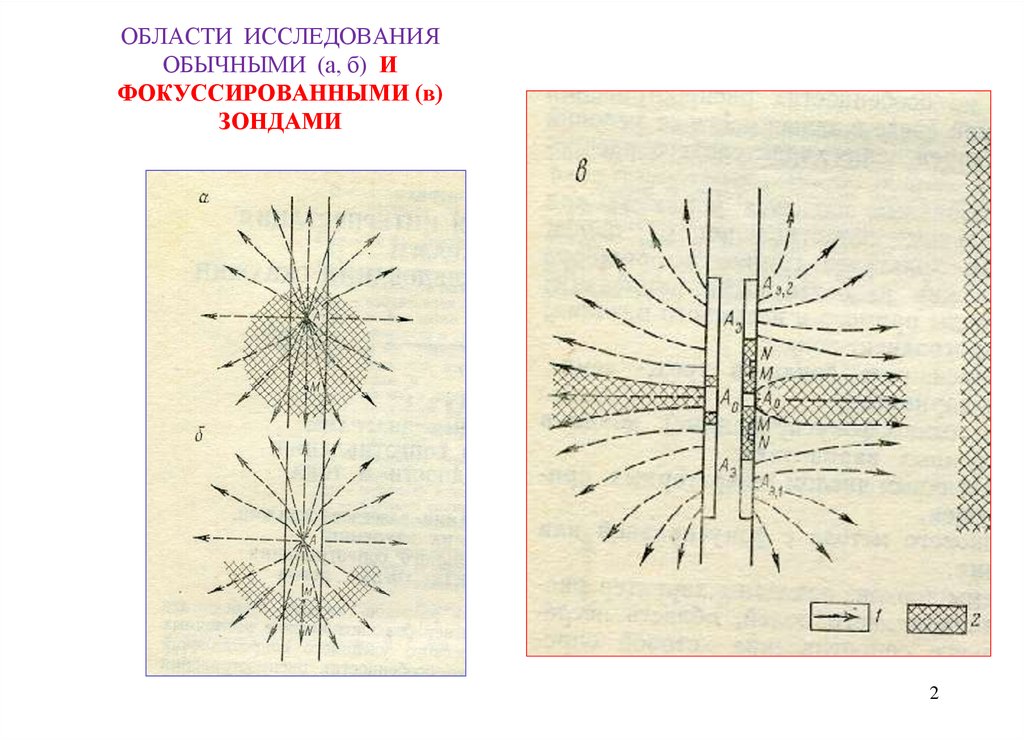
12. ОБЛАСТИ ИССЛЕДОВАНИЯ ОБЫЧНЫМИ (а, б) И ФОКУССИРОВАННЫМИ (в) ЗОНДАМИ
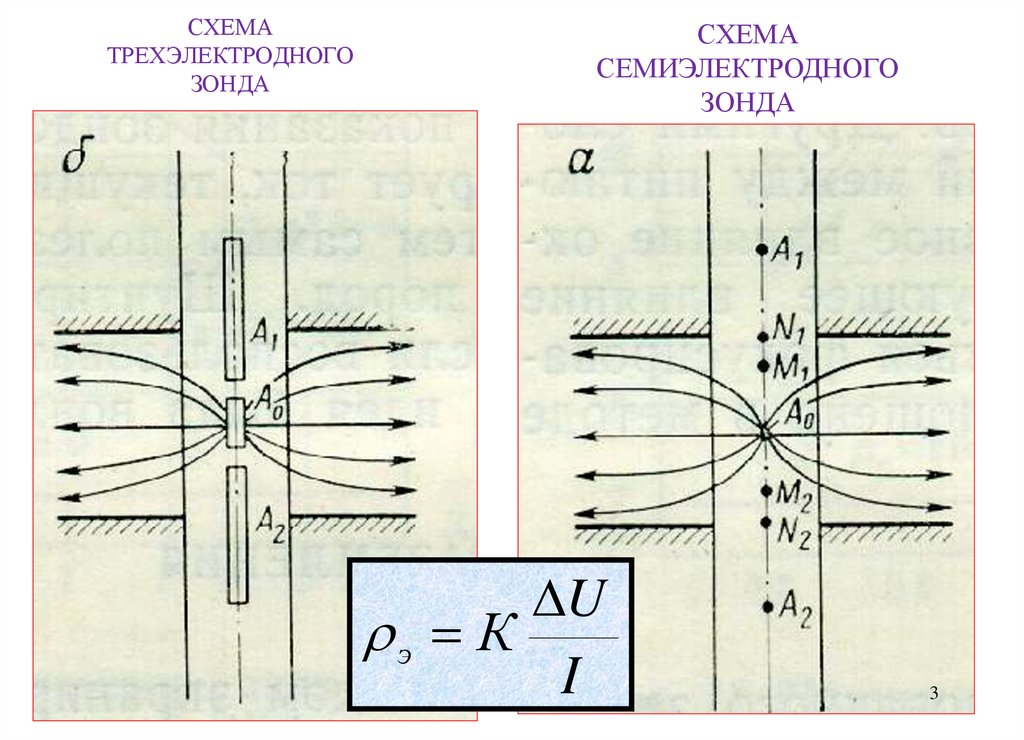
23. СХЕМА ТРЕХЭЛЕКТРОДНОГО ЗОНДА
СХЕМАСЕМИЭЛЕКТРОДНОГО
ЗОНДА
U
э К
I
3
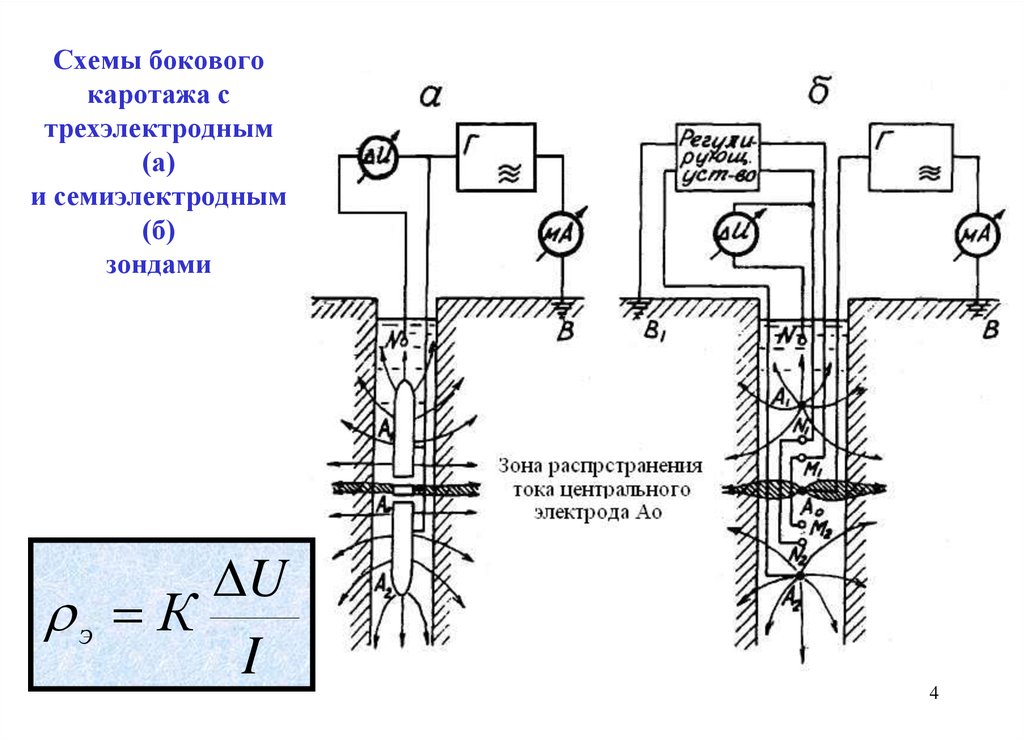
4. Схемы бокового каротажа с трехэлектродным (а) и семиэлектродным (б) зондами
Uэ К
I
4
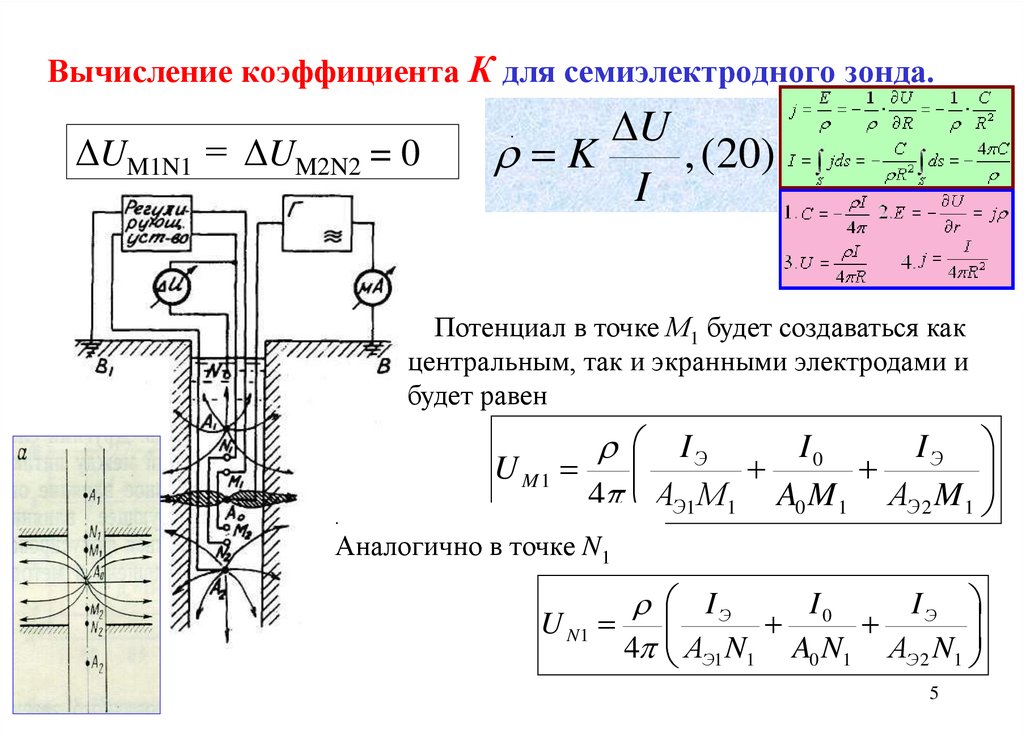
5. Вычисление коэффициента К для семиэлектродного зонда.
ΔUM1N1 = ΔUM2N2 = 0U
K
, (20)
I
.
Потенциал в точке М1 будет создаваться как
центральным, так и экранными электродами и
будет равен
.
I0
IЭ
IЭ
U M1
4 АЭ1М 1 A0 M 1 АЭ 2 M 1
Аналогично в точке N1
I0
IЭ
IЭ
U N1
4 АЭ1 N1 A0 N1 АЭ 2 N1
5
6. Вычисление коэффициента К для семиэлектродного зонда.
По условию UM1=UN1, следовательноIЭ
I0
IЭ
IЭ
I0
IЭ
АЭ1 М 1 A0 M 1 АЭ 2 M 1 АЭ1 N1 A0 N1 АЭ 2 N1
или
1
1
1
1
1
I Ý
I 0
A0 M1 A0 N1
ÀÝ 1 N1 ÀÝ 2 N1 ÀÝ 1Ì
1
ÀÝ 2 M1
1
IЭ = сI0.
Разность потенциалов ΔUNN1 будет численно равна потенциалу
электрода N1
U NN1
U N1
I
I
IЭ
0 Э
4 АЭ1 N1 A0 N1 АЭ 2 N1 IЭ = сI0.
I0 c
1
c
(21)
4 АЭ1 N1 A0 N1 АЭ 2 N1
6
7. Вычисление коэффициента К для семиэлектродного зонда.
4U
U
K
I0
c
1
c I0
АЭ1 N1 A0 N1 АЭ 2 N1
K
4
c
1
c
АЭ1 N1 A0 N1 АЭ 2 N1
7
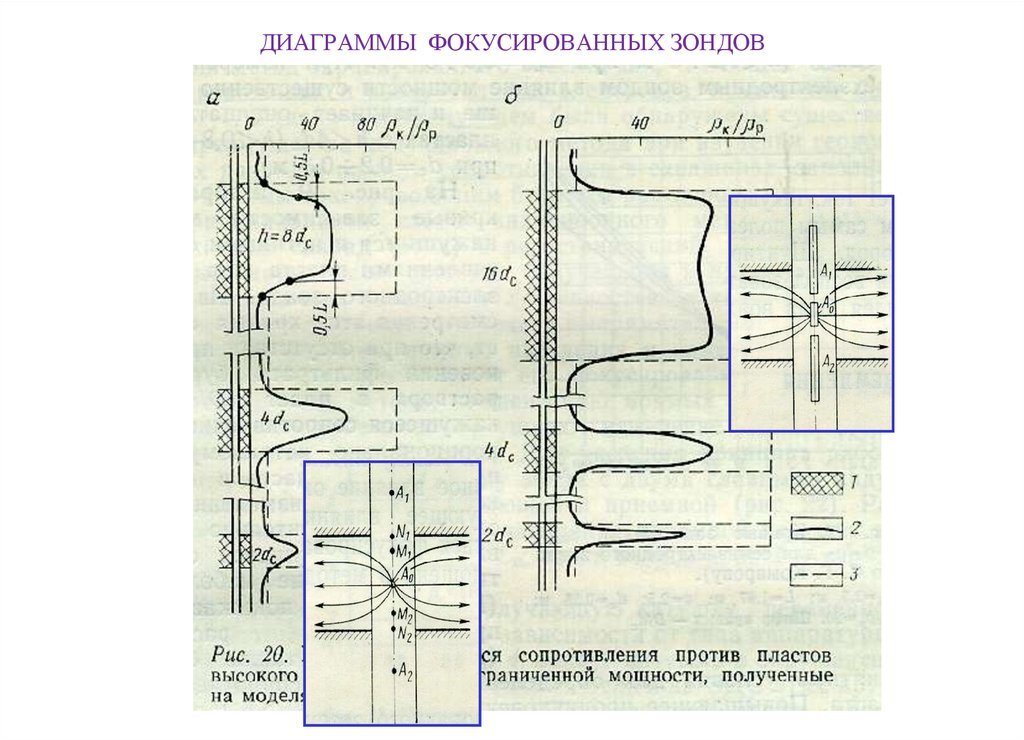
8. ДИАГРАММЫ ФОКУСИРОВАННЫХ ЗОНДОВ
9. Понятие геометрического фактора в методе БК. Модель к расчету общего сопротивления среды.
lΔRi= i
S
r
Ri i
2 ri L
r
bi
ri
дифференциальный
геометрический фактор
Функция b = f(r) представляет гиперболу.
с
зп
п
к
biф
b
b
b
ic
iзп
in
2 L 0
2 L 0
2 L d
2 L D
d
D
9
10. Понятие геометрического фактора в методе БК. Интегральный геометрический фактор.
ρк = ρс Вс + ρзп Взп + ρп Вп(24)
Анализ формулы (24) позволяет сделать следующие выводы:
1. Геометрические факторы не зависят от электрических параметров
среды, а лишь от геометрии изучаемого пространства;
2. БК наиболее эффективен в скважинах, вскрытых на соленых
растворах ( ↓ρс ), и при высоком сопротивлении пород (↑ ρп );
3.Так как Вj представляет собой отношение части пространства,
представленного скважиной, зоной проникновения и неизмененным
пластом ко всему пространству, то геометрический фактор
характеризует вклад той или иной части пространства в измеряемое
ρк ;
10
11. Понятие геометрического фактора в методе БК. Интегральный геометрический фактор.
ρк = ρс Вс + ρзп Взп + ρп Вп(24)
Анализ формулы (24) позволяет сделать следующие выводы:
4. Сумма геометрических факторов
с d
зп D
к
Так как
Вс + Взп + Вп = 1.
п
biф
bic
biзп
bin
2 L 0
2 L 0
2 L d
2 L D
1
r dr ln r
r
bi
ri
то зависимость В=f(r) будет представлять собой
логарифмическую функцию, асимптотически
приближающуюся к единице.
11
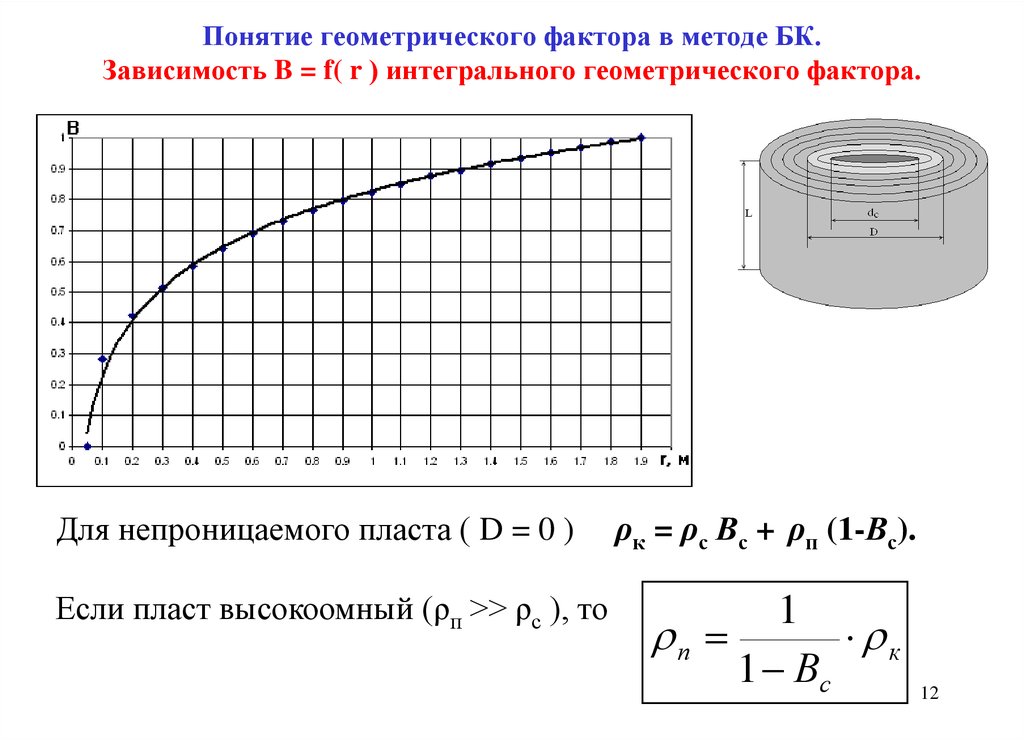
12. Понятие геометрического фактора в методе БК. Зависимость B = f( r ) интегрального геометрического фактора.
Для непроницаемого пласта ( D = 0 )Если пласт высокоомный (ρп >> ρс ), то
ρк = ρс Вс + ρп (1-Вс).
1
п
к
1 Вс
12






 Физика
Физика








