Геометрические образы, автоматных отображений

1.

Министерство образования и науки Российской Федерации
ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ
ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ОБРАЗОВАНИЯ
«САРАТОВСКИЙ НАЦИОНАЛЬНЫЙ ИССЛЕДОВАТЕЛЬСКИЙ
ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ИМЕНИ Н.Г. ЧЕРНЫШЕВСКОГО»
Кафедра дискретной математики и
информационных технологий
ГЕОМЕТРИЧЕСКИЕ ОБРАЗЫ АВТОМАТНЫХ ОТОБРАЖЕНИЙ
КУРСОВАЯ РАБОТА
Студентки 3 курса 321 группы
направления 09.03.01 — Информатика и вычислительная техника
факультета КНиИТ
Бобковой Дианы Андреевны
Научный руководитель
к. ф.-м.н., доцент Тяпаев Л. Б.
Саратов 2016

2.

ЦЕЛЬ
РАБОТЫ
Проведение вычислительных экспериментов, а именно,
построение проекций автоматных отображений Евклидовой
плоскости, представленными геометрическими образами –
множествами точек с рациональными координатами.
ЗАДАЧА
Реализация программы и исследование разнообразия
графиков, полученных данным способом автоматных
отображений

3.

БАЗОВЫЕ ПОНЯТИЯ
Автомат — шестерка объектов , где — множество состояний автомата, — входной
алфавит автомата, – выходной алфавит автомата,
— функция переходов, — функция выходов,
— начальное состояние.
Зафиксируем целое число . Обозначим через множество всех бесконечных
последовательностей , где , и зададим на операции сложения и умножения.
Множество с операциями сложения и умножения называется кольцом целых
адических чисел.

Каждому автомату соответствует отображение в , для всех
.

4.

БАЗОВЫЕ ПОНЯТИЯ
Объектом исследования является автоматное преобразование кольца в контексте
адической динамики: автоматы рассматриваются как динамические системы на
фазовом пространстве .
Тройка , где – измеримое пространство, снабженное мерой , , называется
динамической системой . Более того, если – метрическое пространство, то, как
правило, непрерывное преобразование относительно метрики на . Пространство
называется фазовым пространством динамической системы.

5.

АВТОМАТНЫЕ ОТОБРАЖЕНИЯ, ЗАДАННЫЕ С
ПОМОЩЬЮ ГЕОМЕТРИЧЕСКИХ ОБРАЗОВ
Каждой
паре в пространстве сопоставляется точка с координатами ,
где:
,,;
,, .
Полученные координаты наносятся на Евклидову плоскость, таким
образом строятся проекций автоматных отображений, с помощью
геометрических образов.

6.

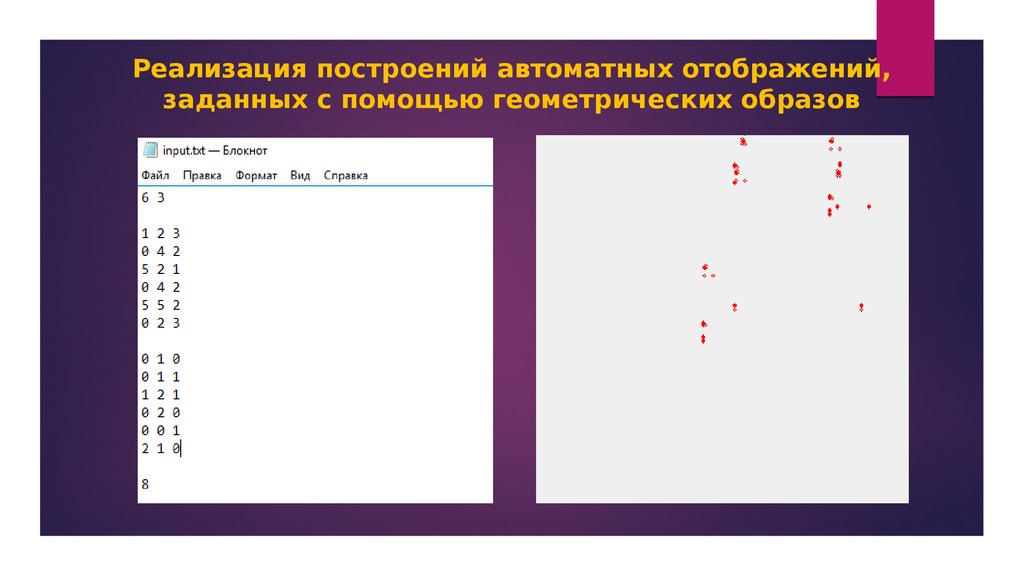
Реализация построений автоматных отображений,
заданных с помощью геометрических образов
Алгоритм работы программы:
1. Программа считывает автомат в виде:
— количество заданных состояний;
— количество входов и выходов;
— таблица переходов;
— таблица выходов;
— желаемая длина последовательности.
2. Генерируются всевозможные последовательности заданной длины.
3. Каждая из сгенерированных последовательностей пропускается через автомат
поразрядно, справа налево.
4. Выходные последовательности записываются аналогично поразрядно справа
налево.
5. Далее по формуле считаются координаты.
6. Полученные координаты точек отмечаются на графике.