Похожие презентации:
Численное моделирование теплообмена в ТВС реактора БН-1200
1. Численное моделирование теплообмена в ТВС реактора БН-1200
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИФедеральное государственное бюджетное образовательное учреждение высшего
профессионального образования
«Национальный исследовательский ядерный университет «МИФИ»
Обнинский институт атомной энергетики – филиал НИЯУ МИФИ
Руководитель дипломной работы: к.т.н., доцент Шелегов А.С. (ИАТЭ)
Студент-дипломник группы Э2-С09: Курашов С.С. (ИАТЭ)
Рецензент: к.т.н, доцент Чусов И.А. (ИАТЭ)
.
Обнинск-2015
2. Введение
В последние время разрабатываются реакторы набыстрых нейтронах. Для разработки проектов
необходимо иметь различные теплогидравлические
коды. Использование кодов позволит своевременно
проводить корректировку в проектировании. В
работе предлагается провести частичную
верификацию одного из зарубежных кодов ANSYS
CFX.
3. Цели работы
разработать расчетные модели для численногомоделирования процесса теплообмена в ТВС
реактора типа БН;
провести численные эксперименты (расчеты) с
целью получения температурных полей и полей
скоростей в теплоносителе (натрий);
провести анализ полученных данных и сравнение
их с эмпирической зависимостью по критерию
Нуссельта.
4. Разработка расчетной 3D модели
Общий вид ТВС и ТВЭЛ реактора БН-1200Твердотельная 3D модель
5. Расчетная модель
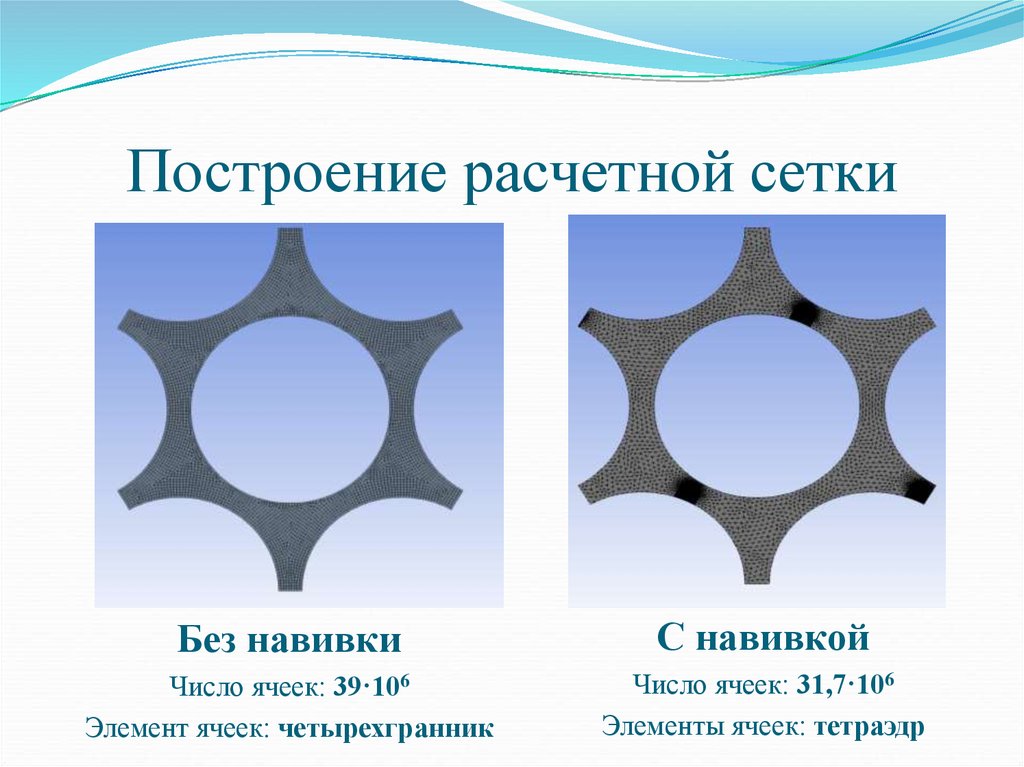
6. Построение расчетной сетки
Без навивкиС навивкой
Число ячеек: 39·106
Элемент ячеек: четырехгранник
Число ячеек: 31,7·106
Элементы ячеек: тетраэдр
7. Постановка граничных условий
- температура натрия на входе в расчетную модель составляет 410 0С;- на выходе относительное давление 0 МПа, что позволяет рассчитать
гидравлические потери ΔP на участке расчетной модели ΔP = Pвх;
- расход натрия составляет через модель 0,32 кг/с;
- для поверхностей со смежными ячейками задавалось условие симметрии;
- задавался постоянный тепловой с поверхности тепловыделяющей части –
767070,8 Вт/м2, соответствующий номинальному уровню мощность N = 2800
МВт(тепловая).
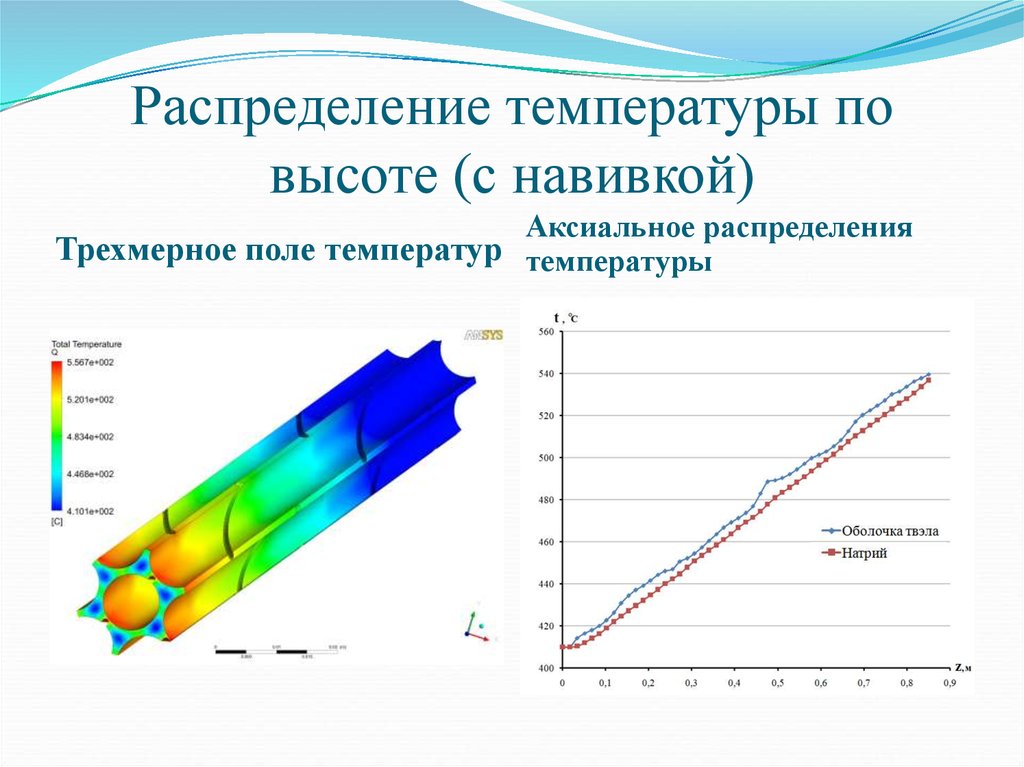
8. Распределение температуры по высоте (с навивкой)
Аксиальное распределенияТрехмерное поле температур температуры
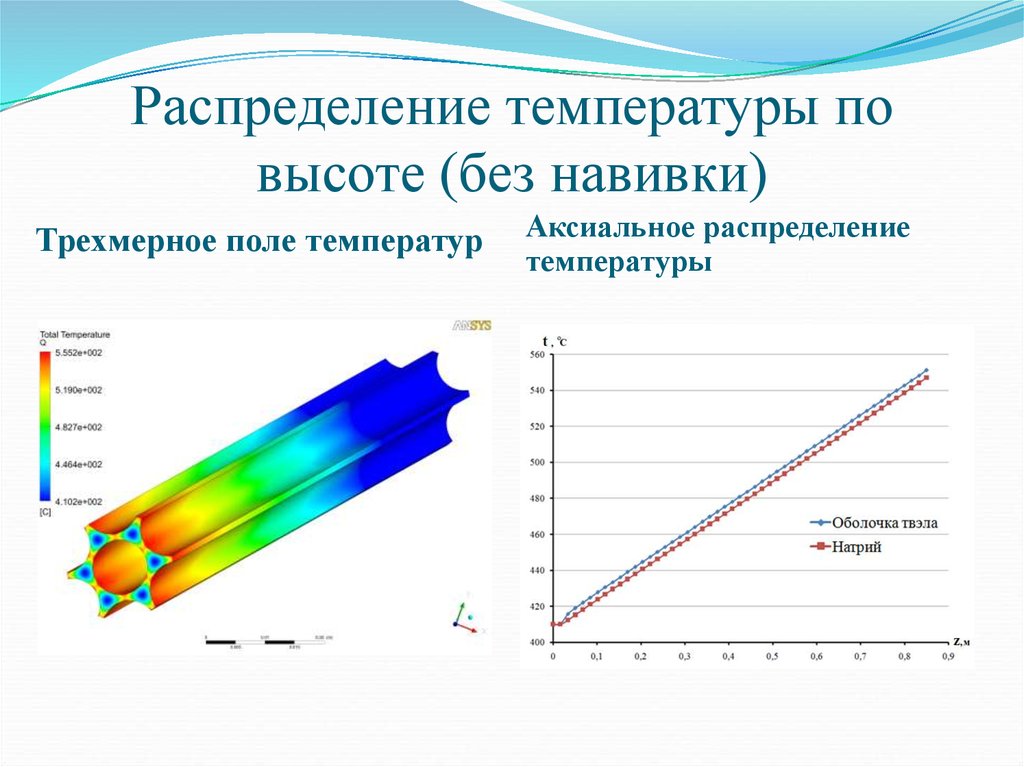
9. Распределение температуры по высоте (без навивки)
Трехмерное поле температурАксиальное распределение
температуры
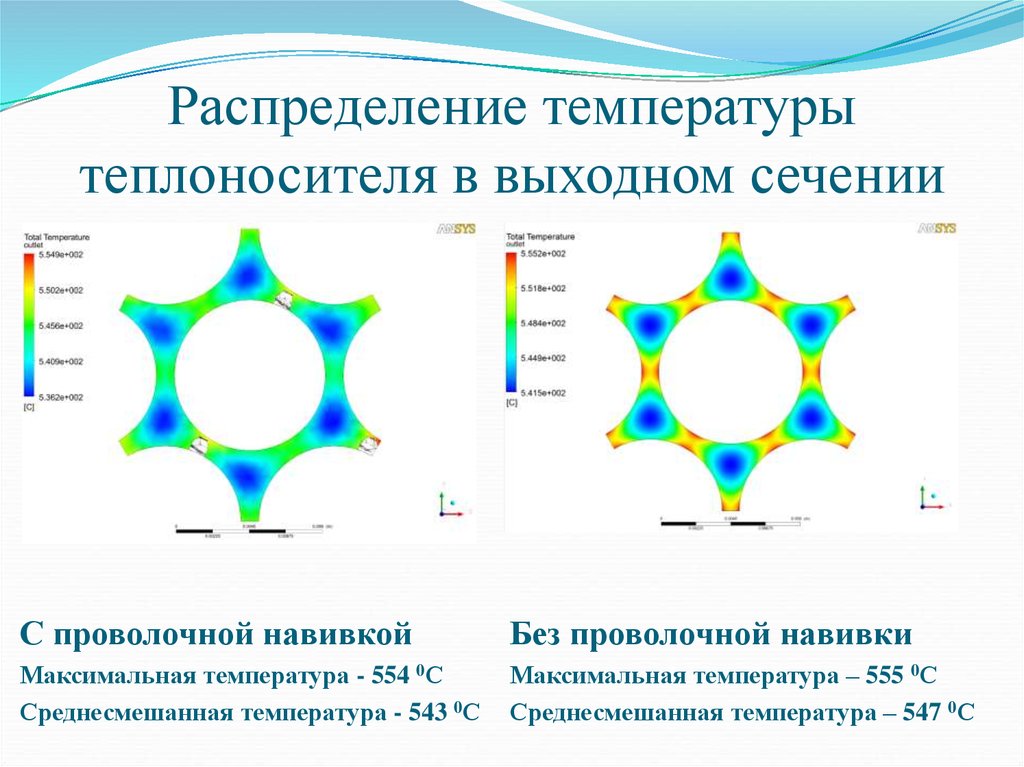
10. Распределение температуры теплоносителя в выходном сечении
С проволочной навивкойБез проволочной навивки
Максимальная температура - 554 0С
Среднесмешанная температура - 543 0С
Максимальная температура – 555 0С
Среднесмешанная температура – 547 0С
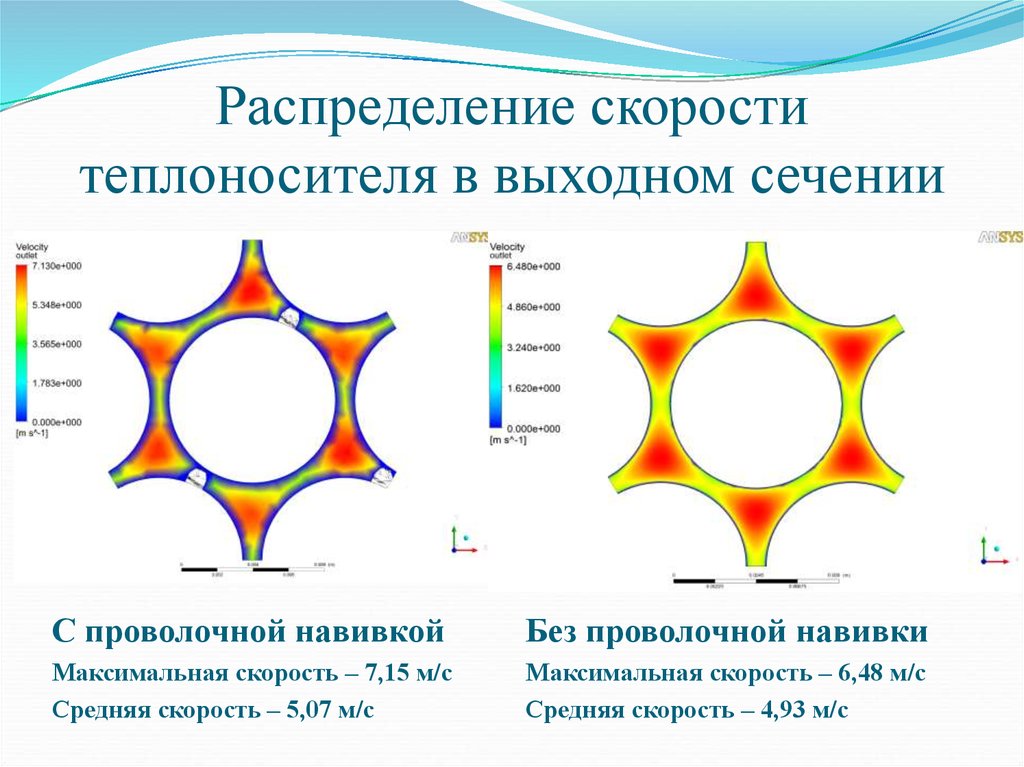
11. Распределение скорости теплоносителя в выходном сечении
С проволочной навивкойБез проволочной навивки
Максимальная скорость – 7,15 м/с
Средняя скорость – 5,07 м/с
Максимальная скорость – 6,48 м/с
Средняя скорость – 4,93 м/с
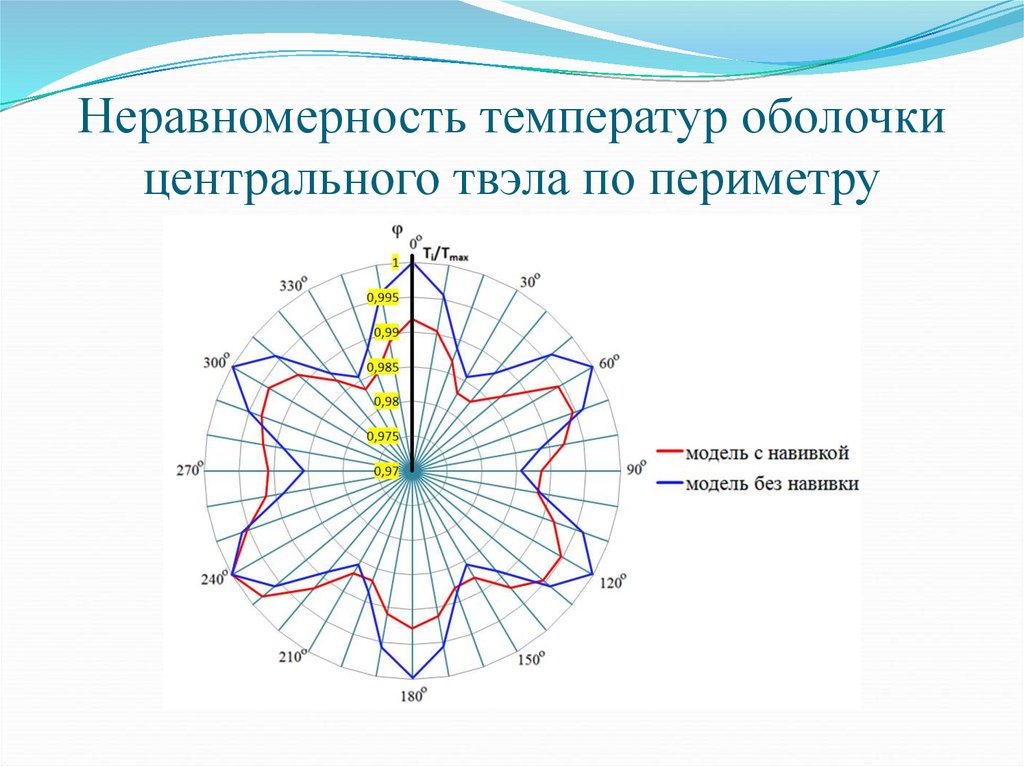
12. Неравномерность температур оболочки центрального твэла по периметру
13. Расчет по эмпирическим зависимостям
Теплоотдача в треугольных решетках твэлов, охлаждаемых жидкими металламирассчитывается по формуле:
Nu = Nuл + f(ε6,s/d)Peφ(s/d)±15%*
1 ≤ s/d ≤ 2;
0,1 ≤ ε6 ≤ ∞;
1 ≤ Pe ≤ 4000;
Где Nuл – число Нуссельта для ламинарного течения теплоносителя;
ε6 – ε-параметр теплового подобия твэлов, рассчитанный по 6 гармонике;
f(ε6,s/d) и φ(s/d) – эмпирические функции.
Параметр эквивалентной теплопроводности для цилиндрических твэлов с одной
оболочкой рассчитывается по формуле:
Nuл = [7,55·s/d –
где
][1-
- теплопроводность топлива;
- теплопроводность натрия.
]*;
ε6 =
- теплопроводность оболочки;
*Источник: методические указания и рекомендации по
теплогидравлическому расчету активных зон быстрых реакторов под
общей редакцией Жукова А.В., Сорокина А.П. PTM 1604.008-88
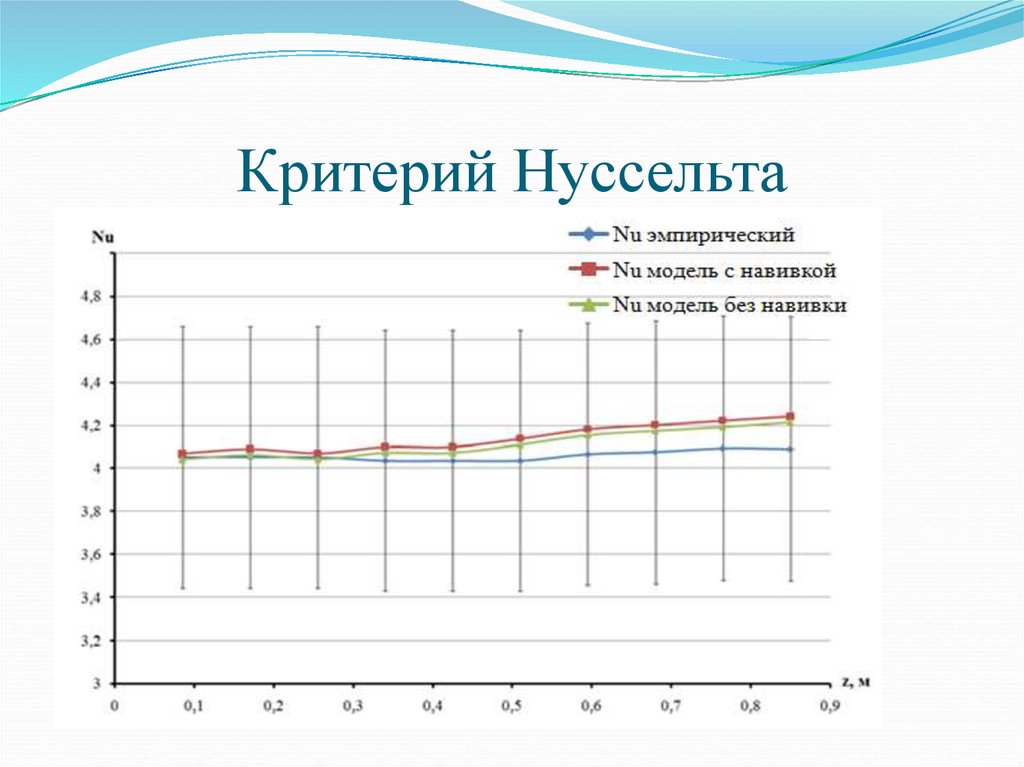
14. Критерий Нуссельта
15. Выводы
Разработаны расчетные 3D модели пучков твэл ТВС БН-1200 с проволочнойнавивкой и без навивки;
Проведены расчеты в результате которых получены поля скоростей и
температур;
Анализ полученных результатов показал, что:
общая неравномерность температур по периметру оболочки твэлов модели
без навивки больше, чем с навивкой, однако, эти неравномерности не
превышают 0,1%;
расчетным путем получены коэффициенты теплоотдачи для модели с
навивкой они оказались большими, чем для модели без навивки;
сравнение результатов расчета с эмпирическими зависимостями показало
неплохое качественное и количественное соответствие, отличие не
превышает 5%, что подтверждает правильность численных экспериментов









 Промышленность
Промышленность








