Похожие презентации:
Лабораторная работа. Параллельные алгоритмы матрично-векторного умножения
1. Лабораторная работа 1. Параллельные алгоритмы матрично-векторного умножения
Нижегородский государственный университетим. Н.И.Лобачевского
Факультет Вычислительной математики и кибернетики
Образовательный комплекс
Введение в методы параллельного
программирования
Лабораторная работа 1.
Параллельные алгоритмы
матрично-векторного умножения
Гергель В.П., профессор, д.т.н.
Кафедра математического
обеспечения ЭВМ
2. Содержание
Упражнения:Постановка задачи
Реализация последовательного алгоритма умножения
матрицы на вектор
Способы распределения данных
Разработка параллельного алгоритма, основанного на
разделении матрицы по строкам
Разработка параллельного алгоритма, основанного на
разделении матрицы по столбцам
Разработка параллельного алгоритма, основанного на
блочном разделении матрицы
Н.Новгород, 2007 г.
Основы параллельных вычислений: Параллельные алгоритмы
матрично-векторного умножения
2 из 40
3. Упражнение 1: Постановка задачи…
Умножение матрицы на векторc A b
или
a0,1 , ..., a0,n 1 b0
c0 a0, 0 ,
...
b1
c1
b
c a
,
a
,
...,
a
m 1,1
m 1, n 1 n 1
m 1 m 1, 0
Задача умножения матрицы на вектор может быть сведена к
выполнению m независимых операций умножения строк матрицы A на
вектор b
n 1
ci ai , b ai j bj , 0 i m
j 0
Н.Новгород, 2007 г.
Основы параллельных вычислений: Параллельные алгоритмы
матрично-векторного умножения
3 из 40
4. Упражнение 1: Постановка задачи
// Serial algorithm of matrix-vector multiplicationfor (i = 0; i < m; i++) {
c[i] = 0;
for (j = 0; j < n; j++) {
c[i] += A[i][j]*b[j]
}
}
Для выполнения матрично-векторного умножения
необходимо выполнить m операций вычисления
скалярного произведения
Трудоемкость вычислений имеет порядок O(mn)
Н.Новгород, 2007 г.
Основы параллельных вычислений: Параллельные алгоритмы
матрично-векторного умножения
4 из 40
5. Упражнение 2: Реализация последовательного алгоритма умножения матрицы на вектор…
Поэтапная разработка последовательного алгоритма:– Задание 1 – Создание проекта MatrixVectorMult
– Задание 2 – Определение размеров объектов и ввод
данных
– Задание 3 – Завершение процесса вычислений
– Задание 4 – Реализация умножения матрицы на вектор
– Задание 5 – Проведение вычислительных
экспериментов
Н.Новгород, 2007 г.
Основы параллельных вычислений: Параллельные алгоритмы
матрично-векторного умножения
5 из 40
6. Упражнение 2: Реализация последовательного алгоритма умножения матрицы на вектор…
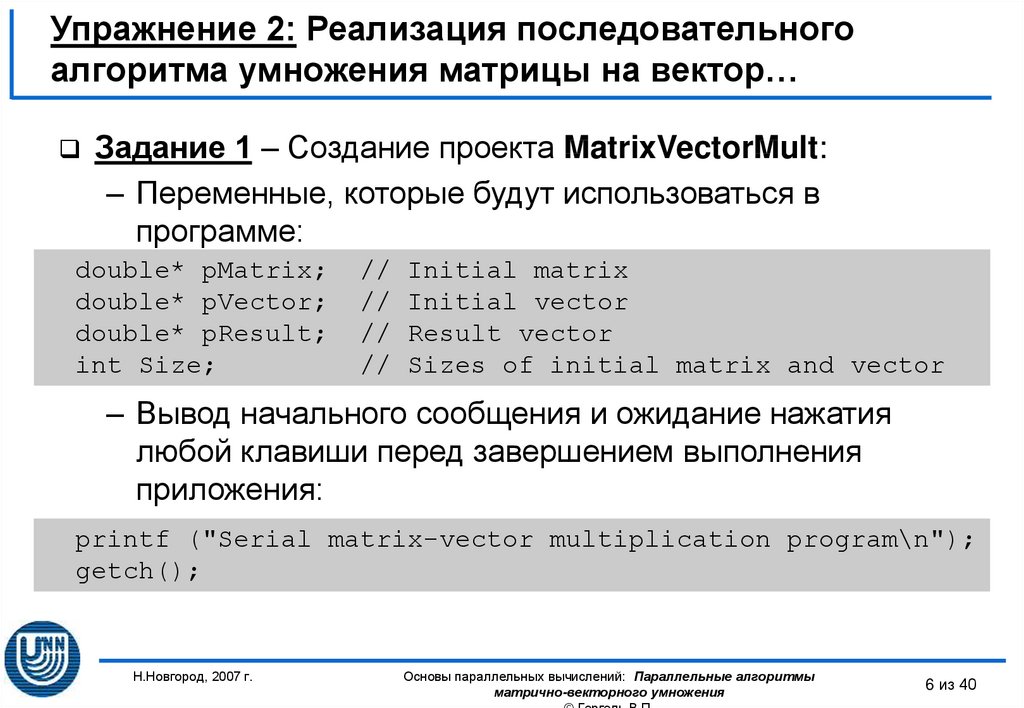
Задание 1 – Создание проекта MatrixVectorMult:– Переменные, которые будут использоваться в
программе:
double* pMatrix;
double* pVector;
double* pResult;
int Size;
//
//
//
//
Initial matrix
Initial vector
Result vector
Sizes of initial matrix and vector
– Вывод начального сообщения и ожидание нажатия
любой клавиши перед завершением выполнения
приложения:
printf ("Serial matrix-vector multiplication program\n");
getch();
Н.Новгород, 2007 г.
Основы параллельных вычислений: Параллельные алгоритмы
матрично-векторного умножения
6 из 40
7. Упражнение 2: Реализация последовательного алгоритма умножения матрицы на вектор…
Задание 2 – Определение размеров объектов и вводданных:…
– Для задания исходных данных реализуем функцию
ProcessInitialization:
• определяет размеры матрицы и вектора,
• выделяет память для всех объектов, участвующих в
умножении (pMatrix, pVector и pResult),
• задает значения элементов исходных матрицы и вектора
// Function for process intialization
void ProcessInitialization (double* &pMatrix,
double* &pVector, double* &pResult, int &Size);
Н.Новгород, 2007 г.
Основы параллельных вычислений: Параллельные алгоритмы
матрично-векторного умножения
7 из 40
8. Упражнение 2: Реализация последовательного алгоритма умножения матрицы на вектор…
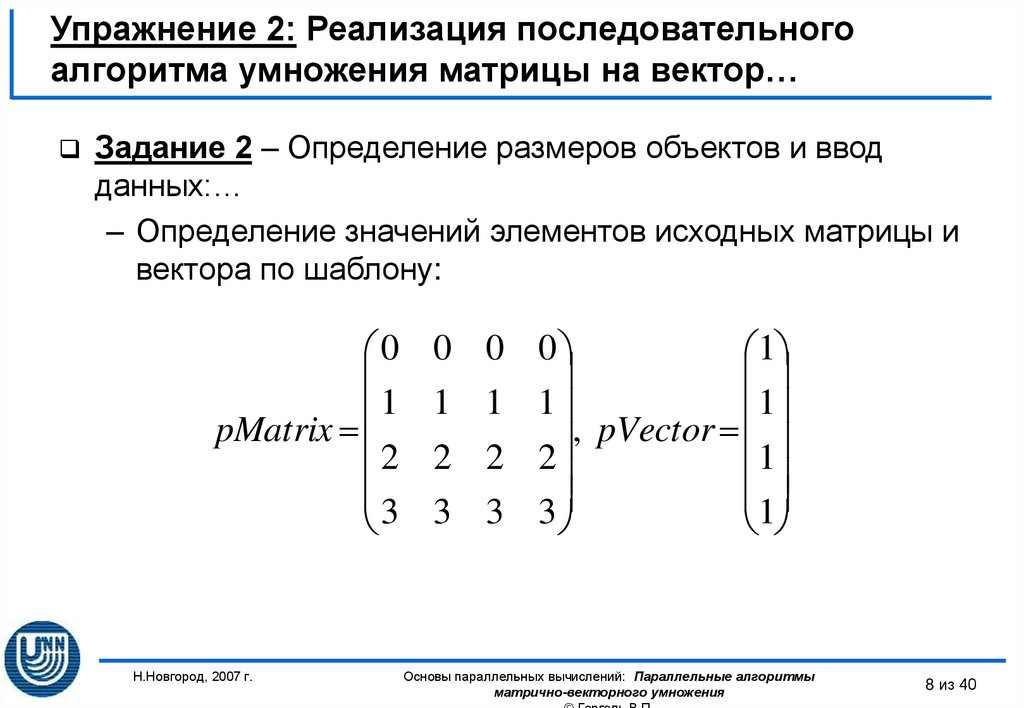
Задание 2 – Определение размеров объектов и вводданных:…
– Определение значений элементов исходных матрицы и
вектора по шаблону:
0
1
pMatrix
2
3
Н.Новгород, 2007 г.
0 0 0
1
1 1 1
1
, pVector
2 2 2
1
1
3 3 3
Основы параллельных вычислений: Параллельные алгоритмы
матрично-векторного умножения
8 из 40
9. Упражнение 2: Реализация последовательного алгоритма умножения матрицы на вектор…
Задание 2 – Определение размеров объектов и вводданных:…
– Функция для простого определения значений
элементов исходных матрицы и вектора:
// Function for simple data initialization
void DummyDataInitialization (double* pMatrix,
double* pVector, int Size)
– Функция для задания значений элементов матрицы и
вектора при помощи датчика случайных чисел:
// Function for random initialization of object elements
void RandomDataInitialization (double* pMatrix,
double* pVector,int Size)
Н.Новгород, 2007 г.
Основы параллельных вычислений: Параллельные алгоритмы
матрично-векторного умножения
9 из 40
10. Упражнение 2: Реализация последовательного алгоритма умножения матрицы на вектор…
Задание 2 – Определение размеров объектов и вводданных:…
– Для контроля правильности задания исходных данных
необходимо разработать:
• Функцию для форматированной печати матрицы PrintMatrix
(входные параметры - матрица pMatrix, количество строк
RowCount и количество столбцов ColCount),
• Функцию для форматированной печати вектора PrintVector
(входные параметры - вектор pVector и количество элементов в
векторе Size)
Н.Новгород, 2007 г.
Основы параллельных вычислений: Параллельные алгоритмы
матрично-векторного умножения
10 из 40
11. Упражнение 2: Реализация последовательного алгоритма умножения матрицы на вектор…
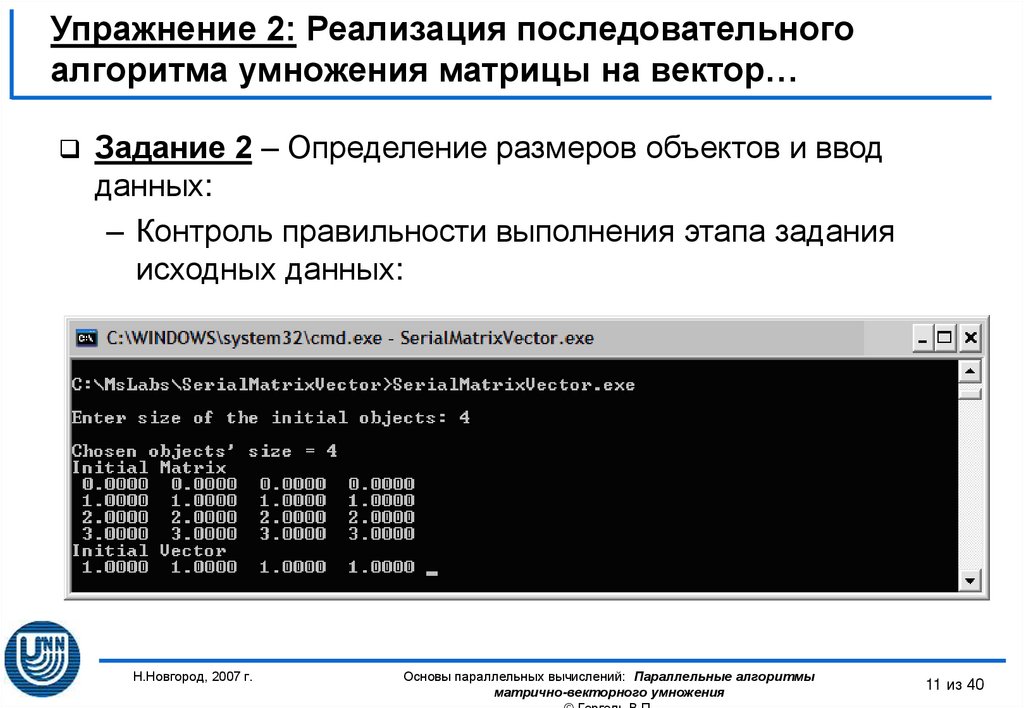
Задание 2 – Определение размеров объектов и вводданных:
– Контроль правильности выполнения этапа задания
исходных данных:
Н.Новгород, 2007 г.
Основы параллельных вычислений: Параллельные алгоритмы
матрично-векторного умножения
11 из 40
12. Упражнение 2: Реализация последовательного алгоритма умножения матрицы на вектор…
Задание 3 – Завершение процесса вычислений:– Функция для корректного завершения процесса
вычислений ProcessTermination:
• Освобождает память, выделенную в ходе выполнения
программы,
• Входные параметры - матрица pMatrix и векторы pVector
и pResult
Н.Новгород, 2007 г.
Основы параллельных вычислений: Параллельные алгоритмы
матрично-векторного умножения
12 из 40
13. Упражнение 2: Реализация последовательного алгоритма умножения матрицы на вектор…
Задание 4 – Реализация умножения матрицы на вектор:…– Функция ResultCalculation выполняет умножение
матрицы на вектор в соответствии с алгоритмом,
изложенным в упражнении 1:
// Function for matrix-vector multiplication
void ResultCalculation (double* pMatrix, double* pVector,
double* pResult, int Size) {
int i, j; // Loop variables
for (i=0; i<Size; i++) {
pResult[i] = 0;
for (j=0; j<Size; j++)
pResult[i] += pMatrix[i*Size+j]*pVector[j];
}
}
Н.Новгород, 2007 г.
Основы параллельных вычислений: Параллельные алгоритмы
матрично-векторного умножения
13 из 40
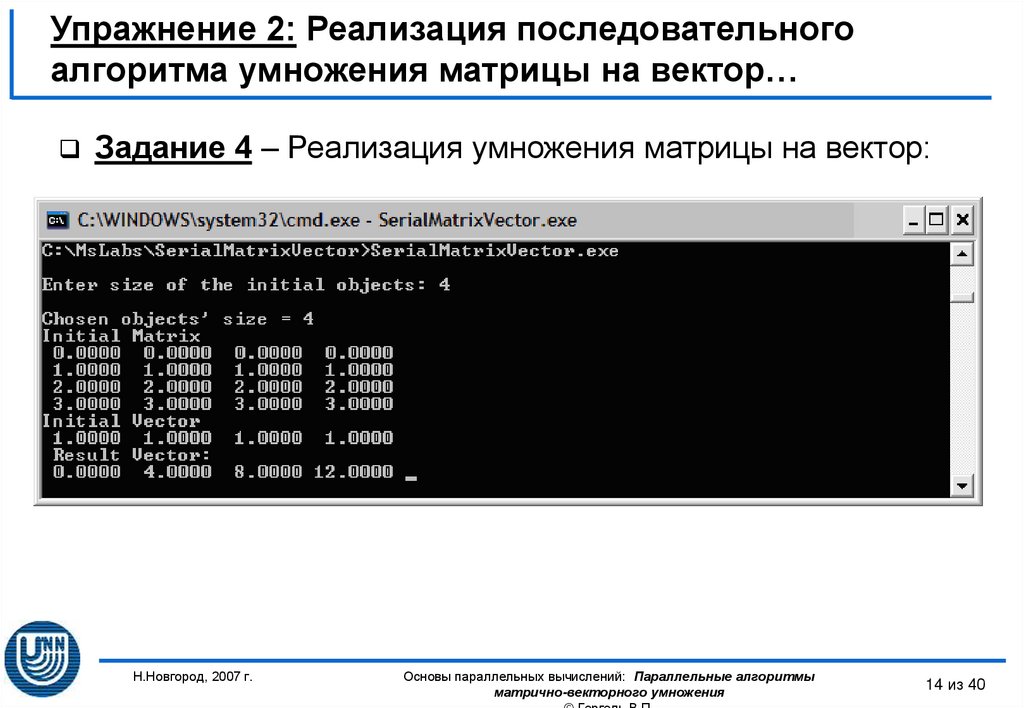
14. Упражнение 2: Реализация последовательного алгоритма умножения матрицы на вектор…
Задание 4 – Реализация умножения матрицы на вектор:Н.Новгород, 2007 г.
Основы параллельных вычислений: Параллельные алгоритмы
матрично-векторного умножения
14 из 40
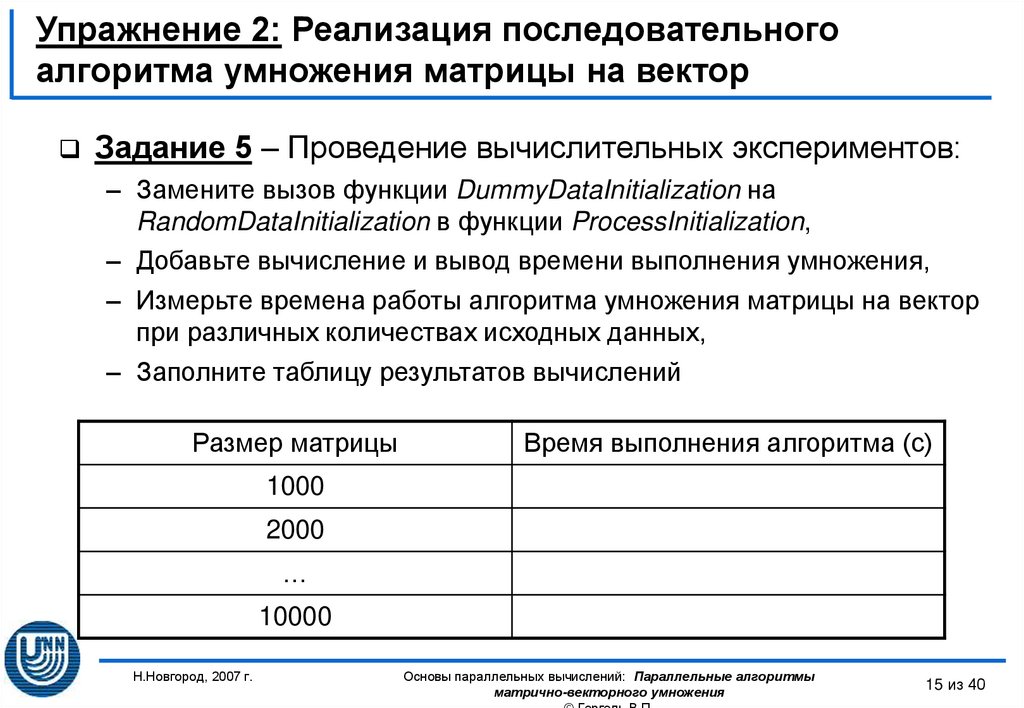
15. Упражнение 2: Реализация последовательного алгоритма умножения матрицы на вектор
Задание 5 – Проведение вычислительных экспериментов:– Замените вызов функции DummyDataInitialization на
RandomDataInitialization в функции ProcessInitialization,
– Добавьте вычисление и вывод времени выполнения умножения,
– Измерьте времена работы алгоритма умножения матрицы на вектор
при различных количествах исходных данных,
– Заполните таблицу результатов вычислений
Размер матрицы
Время выполнения алгоритма (с)
1000
2000
…
10000
Н.Новгород, 2007 г.
Основы параллельных вычислений: Параллельные алгоритмы
матрично-векторного умножения
15 из 40
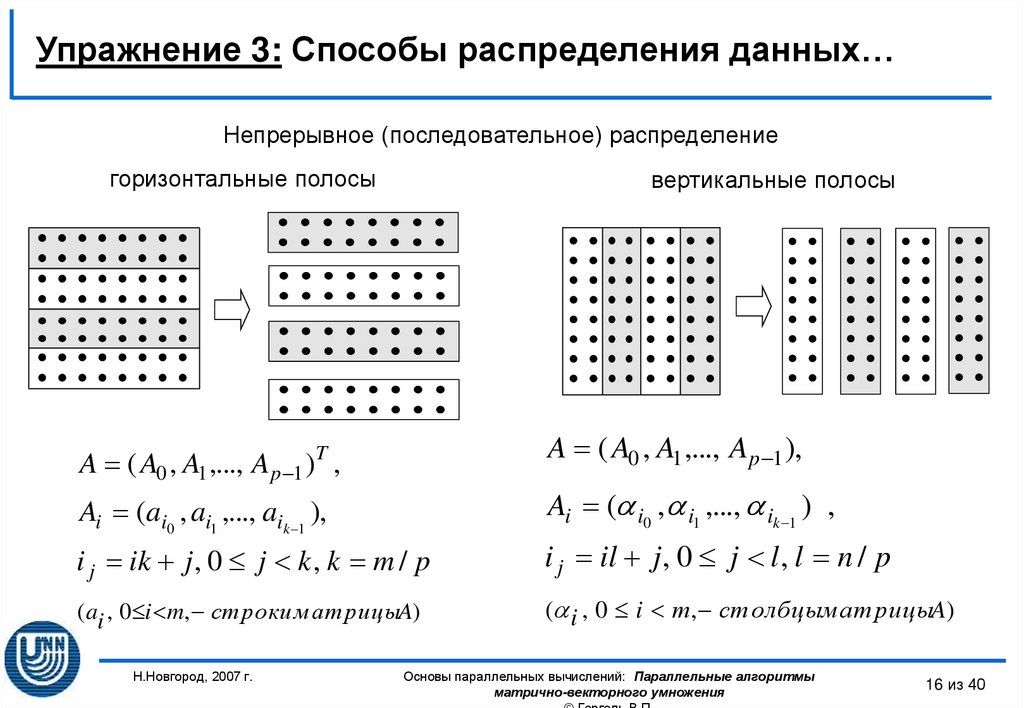
16. Упражнение 3: Способы распределения данных…
Непрерывное (последовательное) распределениегоризонтальные полосы
вертикальные полосы
A ( A0 , A1 ,..., A p 1 ),
A ( A0 , A1 ,..., Ap 1 )T ,
Ai ( i0 , i1 ,..., ik 1 ) ,
Ai (ai0 , ai1 ,..., aik 1 ),
i j ik j , 0 j k , k m / p
i j il j , 0 j l , l n / p
( ai , 0 i m, ст роки м ат рицыA)
( i , 0 i т, ст олбцым ат рицыA)
Н.Новгород, 2007 г.
Основы параллельных вычислений: Параллельные алгоритмы
матрично-векторного умножения
16 из 40
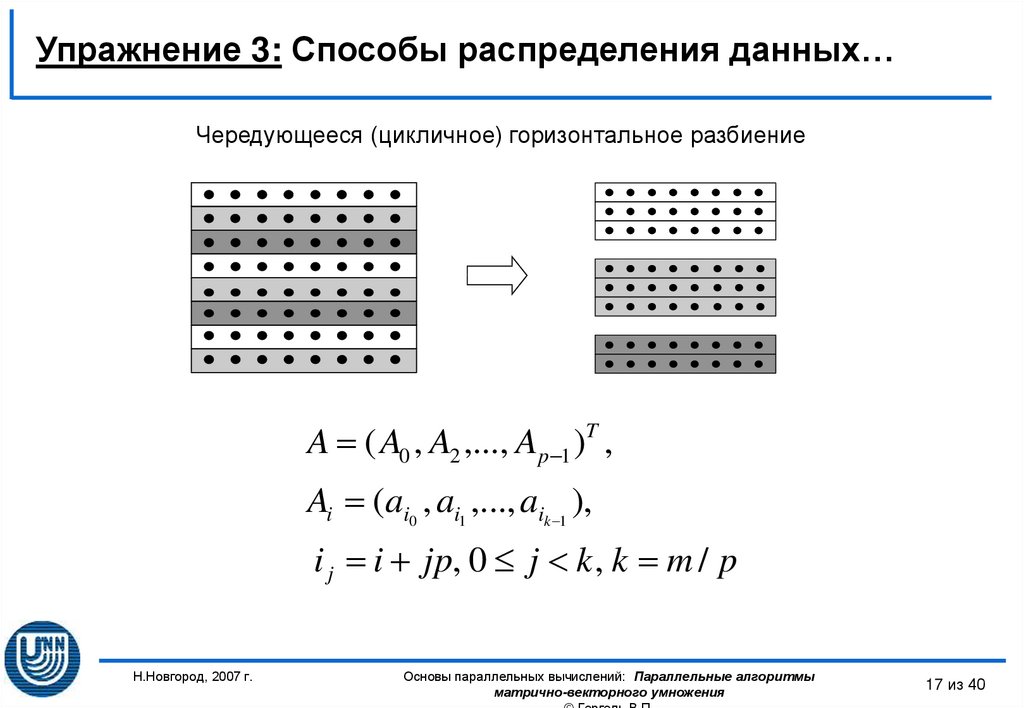
17. Упражнение 3: Способы распределения данных…
Чередующееся (цикличное) горизонтальное разбиениеA ( A0 , A2 ,..., Ap 1 )T ,
Ai (ai0 , ai1 ,..., aik 1 ),
i j i jp, 0 j k , k m / p
Н.Новгород, 2007 г.
Основы параллельных вычислений: Параллельные алгоритмы
матрично-векторного умножения
17 из 40
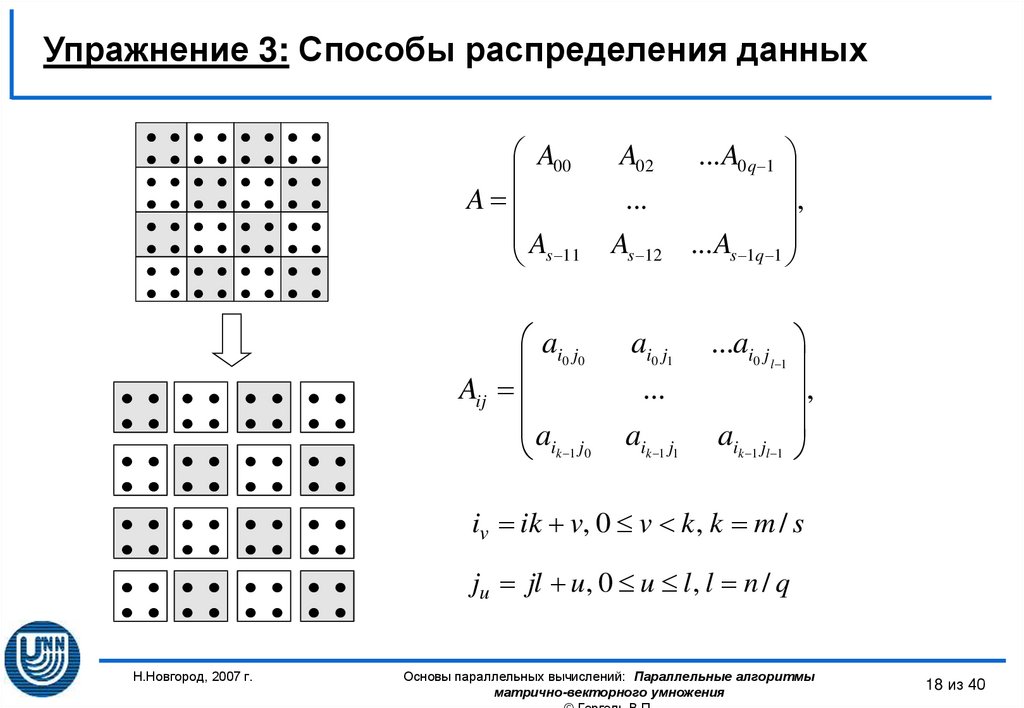
18. Упражнение 3: Способы распределения данных
A00A
A
s 11
ai0 j0
Aij
aik 1 j0
A02
...
As 12
ai0 j1
...
aik 1 j1
... A0 q 1
,
... As 1q 1
...ai0 j
l 1
,
aik 1 jl 1
iv ik v, 0 v k , k m / s
ju jl u, 0 u l , l n / q
Н.Новгород, 2007 г.
Основы параллельных вычислений: Параллельные алгоритмы
матрично-векторного умножения
18 из 40
19. Упражнение 4: Разработка параллельного алгоритма, основанного на разделении матрицы по строкам…
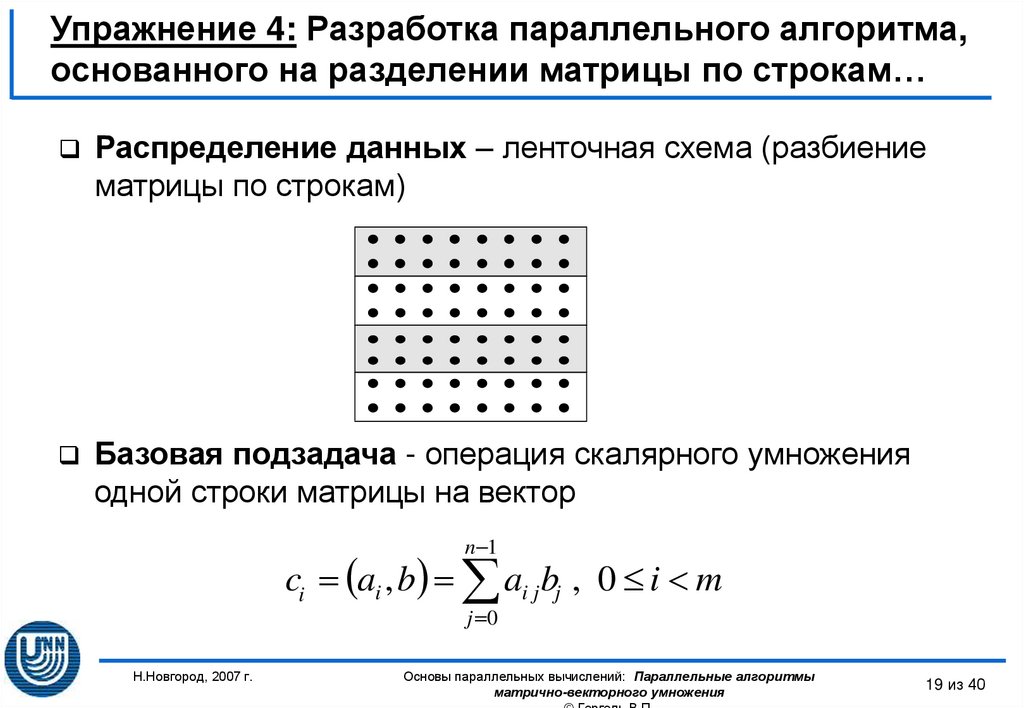
Распределение данных – ленточная схема (разбиениематрицы по строкам)
Базовая подзадача - операция скалярного умножения
одной строки матрицы на вектор
n 1
ci ai , b ai j bj , 0 i m
j 0
Н.Новгород, 2007 г.
Основы параллельных вычислений: Параллельные алгоритмы
матрично-векторного умножения
19 из 40
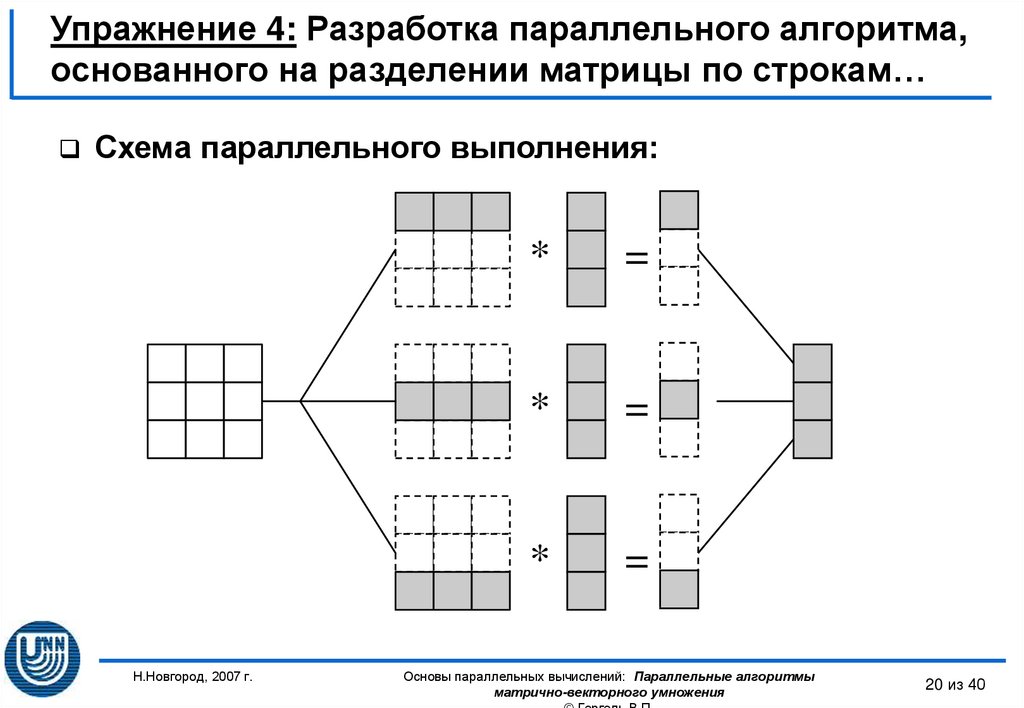
20. Упражнение 4: Разработка параллельного алгоритма, основанного на разделении матрицы по строкам…
Схема параллельного выполнения:Н.Новгород, 2007 г.
*
=
*
=
*
=
Основы параллельных вычислений: Параллельные алгоритмы
матрично-векторного умножения
20 из 40
21. Упражнение 4: Разработка параллельного алгоритма, основанного на разделении матрицы по строкам…
Программная реализация:// Function for calculating matrix-vector multiplication
void ParallelResultCalculation(double* pMatrix, double* pVector,
double* pResult, int Size) {
int i, j; // Loop variables
#pragma omp parallel for private (j)
for (i=0; i<Size; i++) {
pResult[i] = 0;
for (j=0; j<Size; j++)
pResult[i] += pMatrix[i*Size+j]*pVector[j];
}
}
Н.Новгород, 2007 г.
Основы параллельных вычислений: Параллельные алгоритмы
матрично-векторного умножения
21 из 40
22. Упражнение 4: Разработка параллельного алгоритма, основанного на разделении матрицы по строкам…
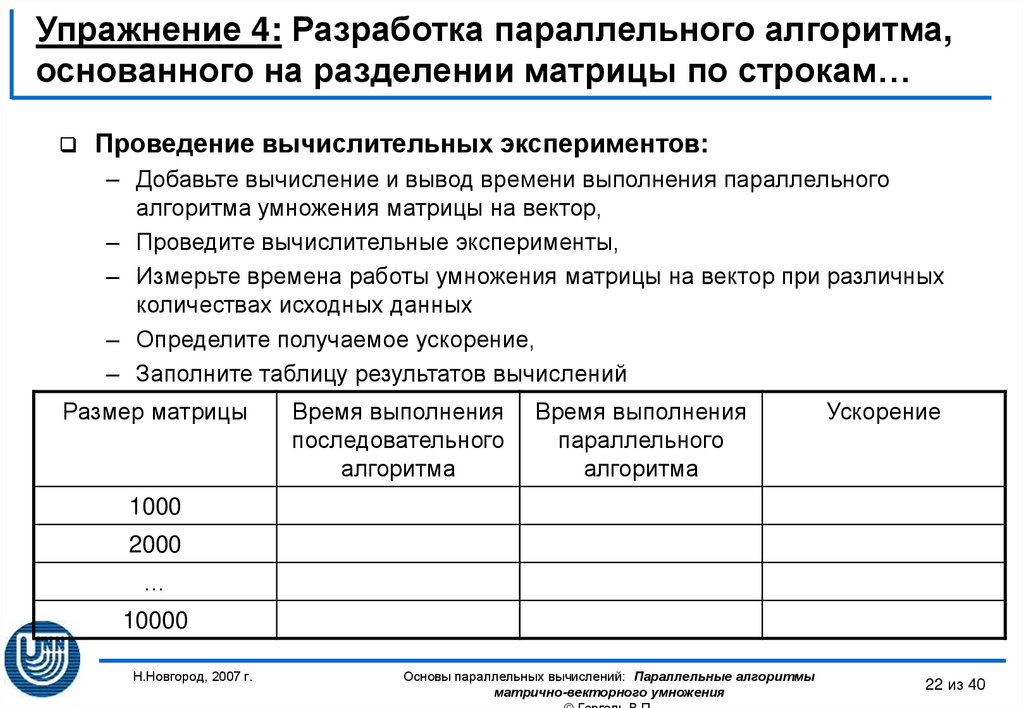
Проведение вычислительных экспериментов:– Добавьте вычисление и вывод времени выполнения параллельного
алгоритма умножения матрицы на вектор,
– Проведите вычислительные эксперименты,
– Измерьте времена работы умножения матрицы на вектор при различных
количествах исходных данных
– Определите получаемое ускорение,
– Заполните таблицу результатов вычислений
Размер матрицы
Время выполнения
последовательного
алгоритма
Время выполнения
параллельного
алгоритма
Ускорение
1000
2000
…
10000
Н.Новгород, 2007 г.
Основы параллельных вычислений: Параллельные алгоритмы
матрично-векторного умножения
22 из 40
23. Упражнение 4: Разработка параллельного алгоритма, основанного на разделении матрицы по строкам…
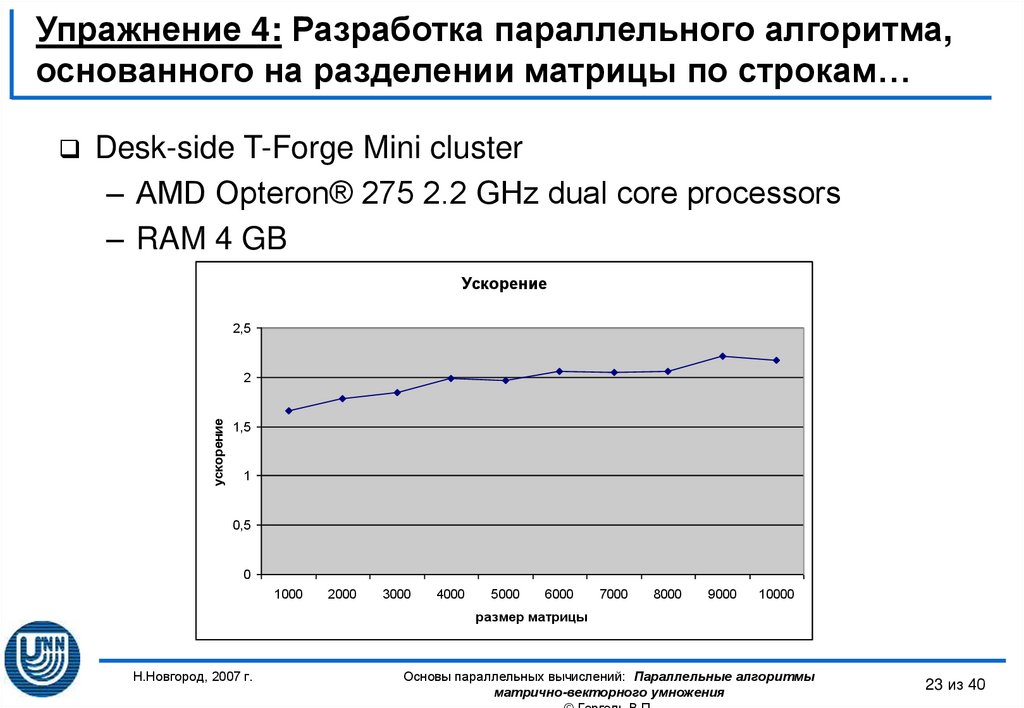
Desk-side T-Forge Mini cluster– AMD Opteron® 275 2.2 GHz dual core processors
– RAM 4 GB
Ускорение
2,5
2
ускорение
1,5
1
0,5
0
1000
2000
3000
4000
5000
6000
7000
8000
9000
10000
размер матрицы
Н.Новгород, 2007 г.
Основы параллельных вычислений: Параллельные алгоритмы
матрично-векторного умножения
23 из 40
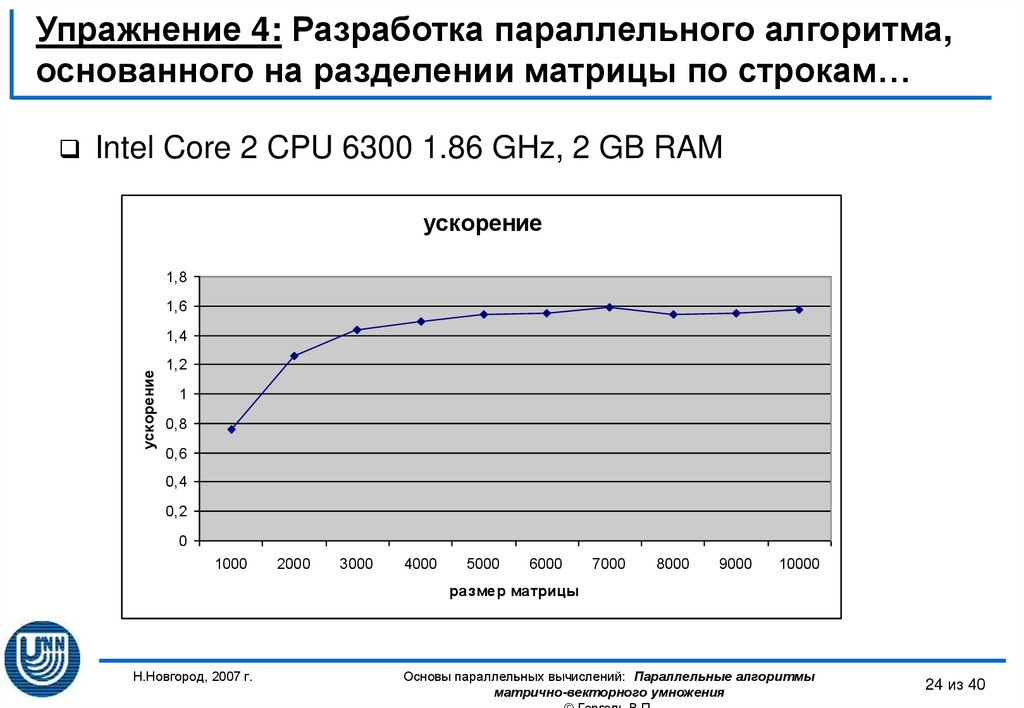
24. Упражнение 4: Разработка параллельного алгоритма, основанного на разделении матрицы по строкам…
Intel Core 2 CPU 6300 1.86 GHz, 2 GB RAMускорение
1,8
1,6
1,4
ускорение
1,2
1
0,8
0,6
0,4
0,2
0
1000
2000
3000
4000
5000
6000
7000
8000
9000
10000
размер матрицы
Н.Новгород, 2007 г.
Основы параллельных вычислений: Параллельные алгоритмы
матрично-векторного умножения
24 из 40
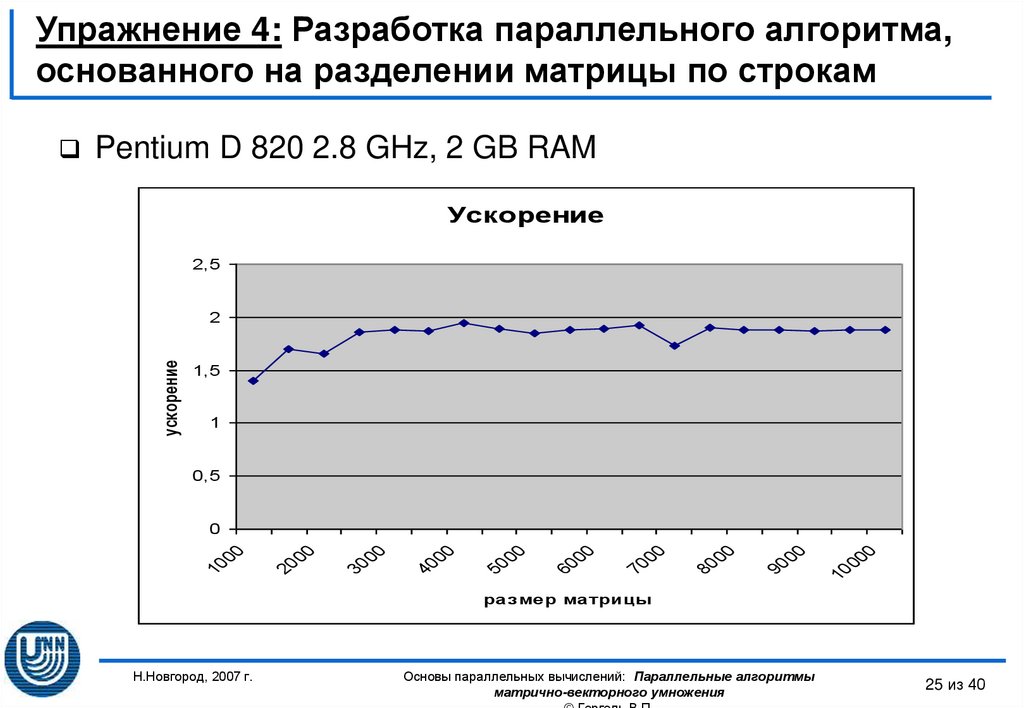
25. Упражнение 4: Разработка параллельного алгоритма, основанного на разделении матрицы по строкам
Pentium D 820 2.8 GHz, 2 GB RAMУскорение
2,5
2
ускорение
1,5
1
0,5
10
00
0
90
00
80
00
70
00
60
00
50
00
40
00
30
00
20
00
0
10
00
размер матрицы
Н.Новгород, 2007 г.
Основы параллельных вычислений: Параллельные алгоритмы
матрично-векторного умножения
25 из 40
26. Упражнение 5: Разработка параллельного алгоритма, основанного на разделении матрицы по столбцам…
Распределение данных – ленточная схема (разбиениематрицы по столбцам)
Базовая подзадача - операция умножения столбца
матрицы А на один из элементов вектора b
Н.Новгород, 2007 г.
Основы параллельных вычислений: Параллельные алгоритмы
матрично-векторного умножения
26 из 40
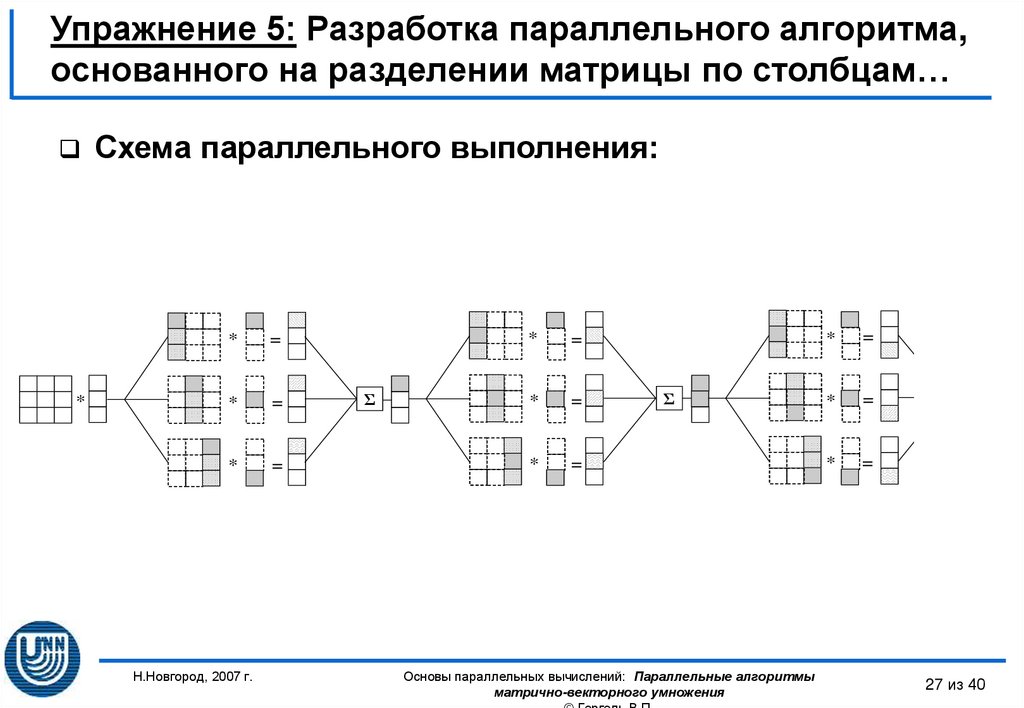
27. Упражнение 5: Разработка параллельного алгоритма, основанного на разделении матрицы по столбцам…
*Схема параллельного выполнения:
*
=
*
=
*
=
Н.Новгород, 2007 г.
Σ
*
=
*
=
*
=
Σ
Основы параллельных вычислений: Параллельные алгоритмы
матрично-векторного умножения
*
=
*
=
*
=
Σ
27 из 40
28. Упражнение 5: Разработка параллельного алгоритма, основанного на разделении матрицы по столбцам…
Программная реализация:// Function for calculating matrix-vector multiplication
void ParallelResultCalculation(double* pMatrix, double* pVector,
double* pResult, int Size) {
int i, j; // Loop variables
double IterGlobalSum = 0;
for (i=0; i<Size; i++) {
IterGlobalSum = 0;
#pragma omp parallel for reduction(+:IterGlobalSum)
for (j=0; j<Size; j++)
IterGlobalSum += pMatrix[i*Size+j]*pVector[j];
pResult[i] = IterGlobalSum;
}
}
Н.Новгород, 2007 г.
Основы параллельных вычислений: Параллельные алгоритмы
матрично-векторного умножения
28 из 40
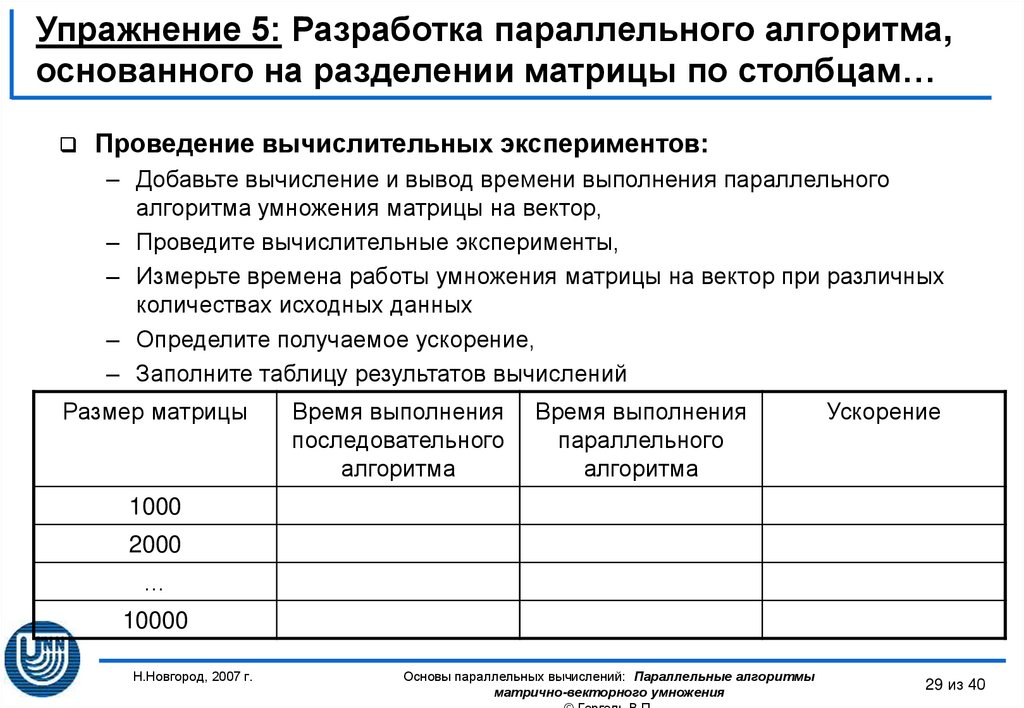
29. Упражнение 5: Разработка параллельного алгоритма, основанного на разделении матрицы по столбцам…
Проведение вычислительных экспериментов:– Добавьте вычисление и вывод времени выполнения параллельного
алгоритма умножения матрицы на вектор,
– Проведите вычислительные эксперименты,
– Измерьте времена работы умножения матрицы на вектор при различных
количествах исходных данных
– Определите получаемое ускорение,
– Заполните таблицу результатов вычислений
Размер матрицы
Время выполнения
последовательного
алгоритма
Время выполнения
параллельного
алгоритма
Ускорение
1000
2000
…
10000
Н.Новгород, 2007 г.
Основы параллельных вычислений: Параллельные алгоритмы
матрично-векторного умножения
29 из 40
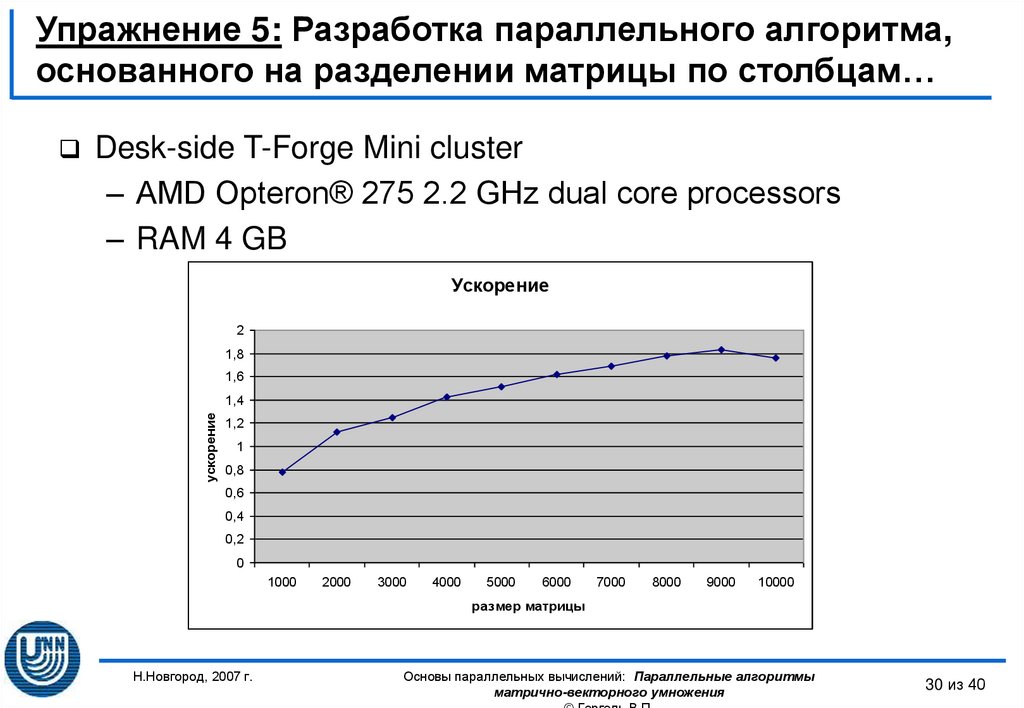
30. Упражнение 5: Разработка параллельного алгоритма, основанного на разделении матрицы по столбцам…
Desk-side T-Forge Mini cluster– AMD Opteron® 275 2.2 GHz dual core processors
– RAM 4 GB
Ускорение
2
1,8
1,6
1,4
ускорение
1,2
1
0,8
0,6
0,4
0,2
0
1000
2000
3000
4000
5000
6000
7000
8000
9000
10000
размер матрицы
Н.Новгород, 2007 г.
Основы параллельных вычислений: Параллельные алгоритмы
матрично-векторного умножения
30 из 40
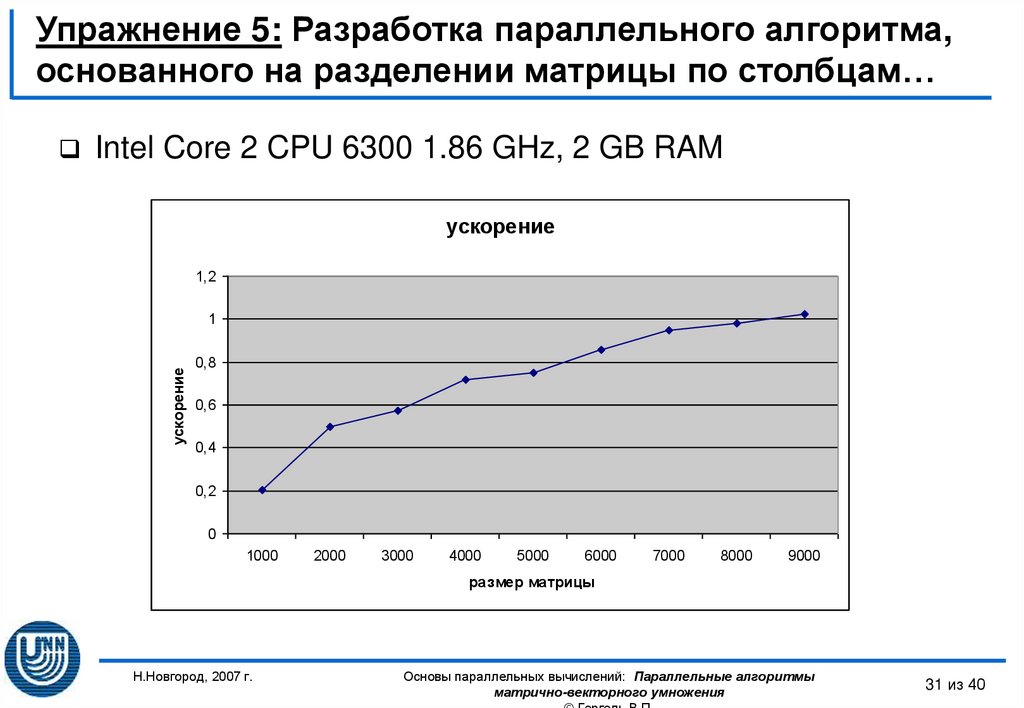
31. Упражнение 5: Разработка параллельного алгоритма, основанного на разделении матрицы по столбцам…
Intel Core 2 CPU 6300 1.86 GHz, 2 GB RAMускорение
1,2
1
ускорение
0,8
0,6
0,4
0,2
0
1000
2000
3000
4000
5000
6000
7000
8000
9000
размер матрицы
Н.Новгород, 2007 г.
Основы параллельных вычислений: Параллельные алгоритмы
матрично-векторного умножения
31 из 40
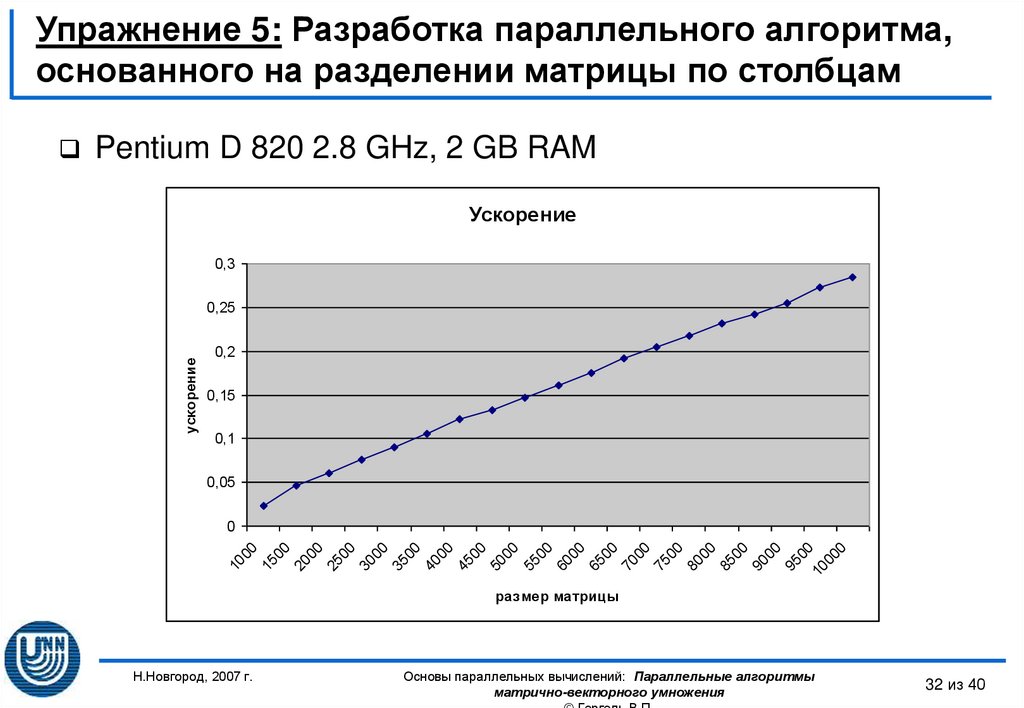
32. Упражнение 5: Разработка параллельного алгоритма, основанного на разделении матрицы по столбцам
Pentium D 820 2.8 GHz, 2 GB RAMУскорение
0,3
0,25
ускорение
0,2
0,15
0,1
0,05
0
10
00
15
00
20
00
25
00
30
00
35
00
40
00
45
00
50
00
55
00
60
00
65
00
70
00
75
00
80
00
85
00
90
00
95
00
10
00
0
размер матрицы
Н.Новгород, 2007 г.
Основы параллельных вычислений: Параллельные алгоритмы
матрично-векторного умножения
32 из 40
33. Упражнение 6: Разработка параллельного алгоритма, основанного на разделении матрицы на блоки…
Распределение данных – блочная схемаБазовая подзадача – умножение блока матрицы A на
блок вектора b
Н.Новгород, 2007 г.
Основы параллельных вычислений: Параллельные алгоритмы
матрично-векторного умножения
33 из 40
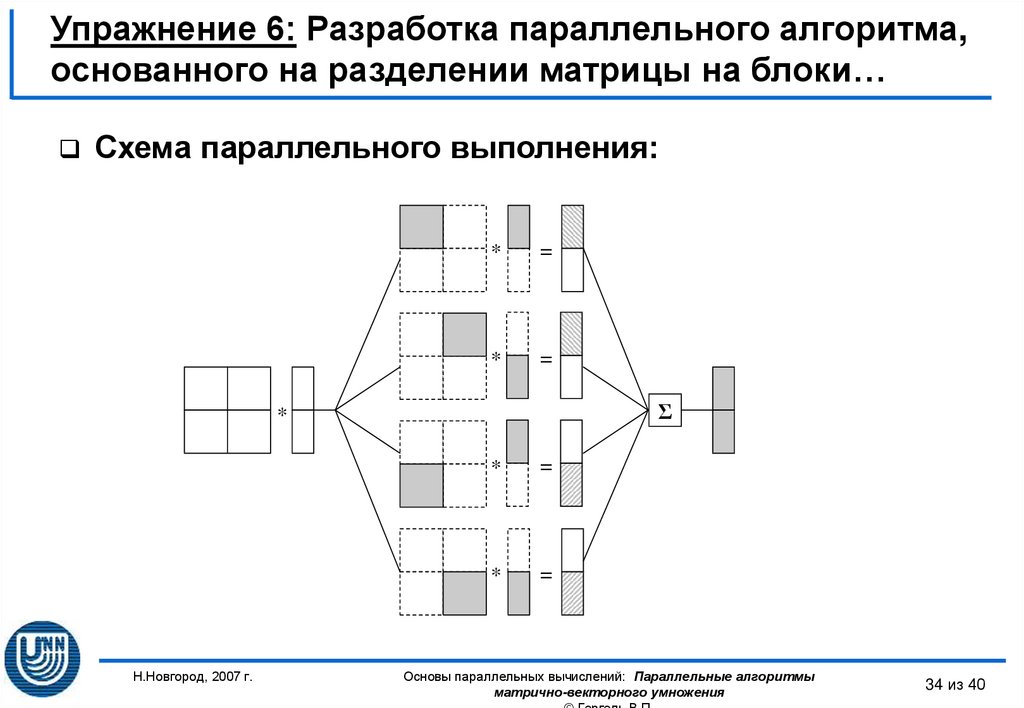
34. Упражнение 6: Разработка параллельного алгоритма, основанного на разделении матрицы на блоки…
Схема параллельного выполнения:*
=
*
=
Σ
*
Н.Новгород, 2007 г.
*
=
*
=
Основы параллельных вычислений: Параллельные алгоритмы
матрично-векторного умножения
34 из 40
35. Упражнение 6: Разработка параллельного алгоритма, основанного на разделении матрицы на блоки…
Программная реализация– Code
Н.Новгород, 2007 г.
Основы параллельных вычислений: Параллельные алгоритмы
матрично-векторного умножения
35 из 40
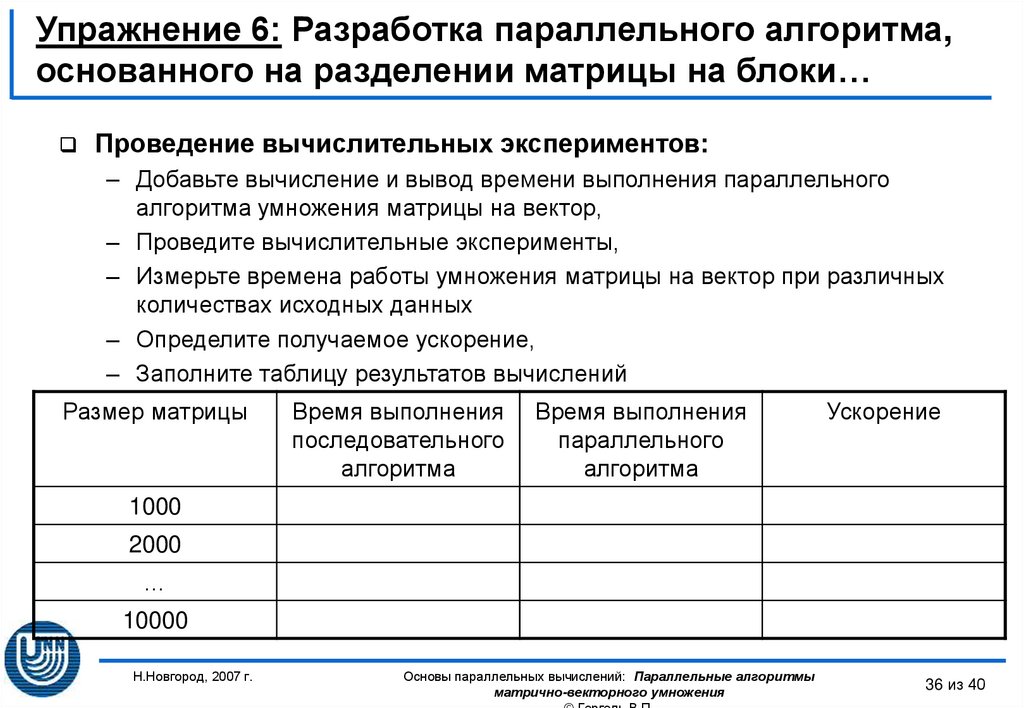
36. Упражнение 6: Разработка параллельного алгоритма, основанного на разделении матрицы на блоки…
Проведение вычислительных экспериментов:– Добавьте вычисление и вывод времени выполнения параллельного
алгоритма умножения матрицы на вектор,
– Проведите вычислительные эксперименты,
– Измерьте времена работы умножения матрицы на вектор при различных
количествах исходных данных
– Определите получаемое ускорение,
– Заполните таблицу результатов вычислений
Размер матрицы
Время выполнения
последовательного
алгоритма
Время выполнения
параллельного
алгоритма
Ускорение
1000
2000
…
10000
Н.Новгород, 2007 г.
Основы параллельных вычислений: Параллельные алгоритмы
матрично-векторного умножения
36 из 40
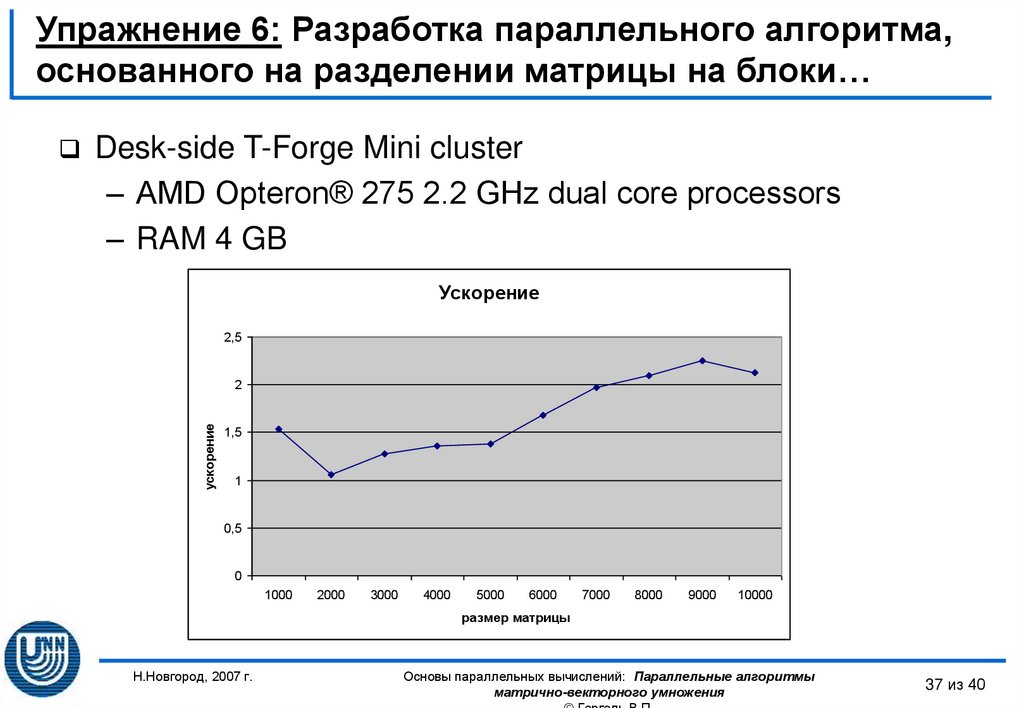
37. Упражнение 6: Разработка параллельного алгоритма, основанного на разделении матрицы на блоки…
Desk-side T-Forge Mini cluster– AMD Opteron® 275 2.2 GHz dual core processors
– RAM 4 GB
Ускорение
2,5
2
ускорение
1,5
1
0,5
0
1000
2000
3000
4000
5000
6000
7000
8000
9000
10000
размер матрицы
Н.Новгород, 2007 г.
Основы параллельных вычислений: Параллельные алгоритмы
матрично-векторного умножения
37 из 40
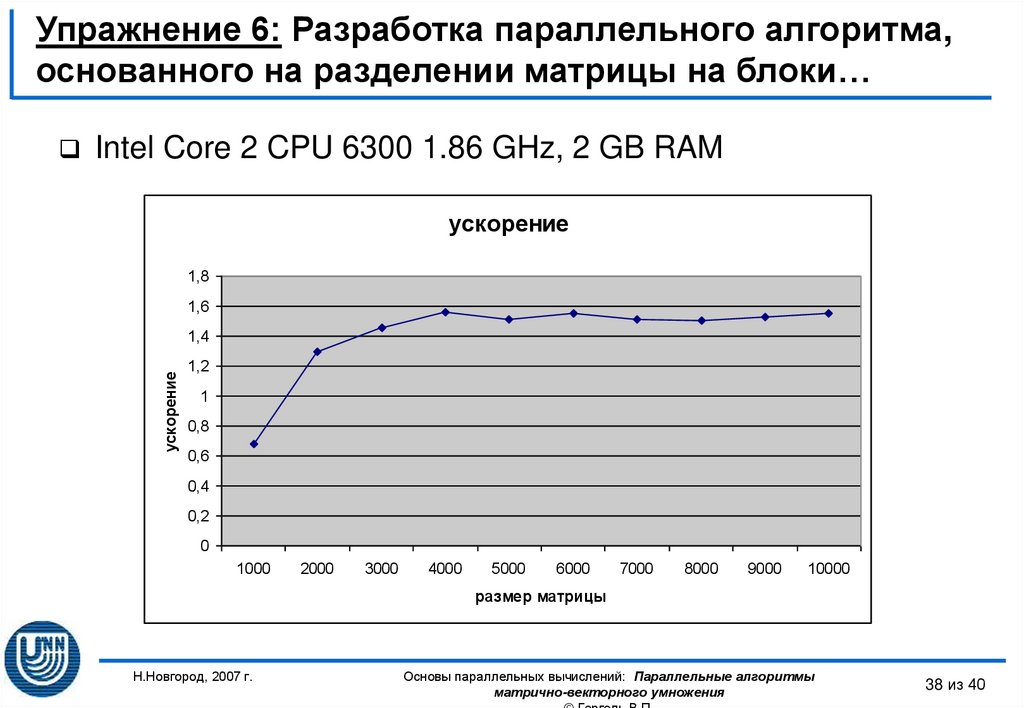
38. Упражнение 6: Разработка параллельного алгоритма, основанного на разделении матрицы на блоки…
Intel Core 2 CPU 6300 1.86 GHz, 2 GB RAMускорение
1,8
1,6
1,4
ускорение
1,2
1
0,8
0,6
0,4
0,2
0
1000
2000
3000
4000
5000
6000
7000
8000
9000
10000
размер матрицы
Н.Новгород, 2007 г.
Основы параллельных вычислений: Параллельные алгоритмы
матрично-векторного умножения
38 из 40
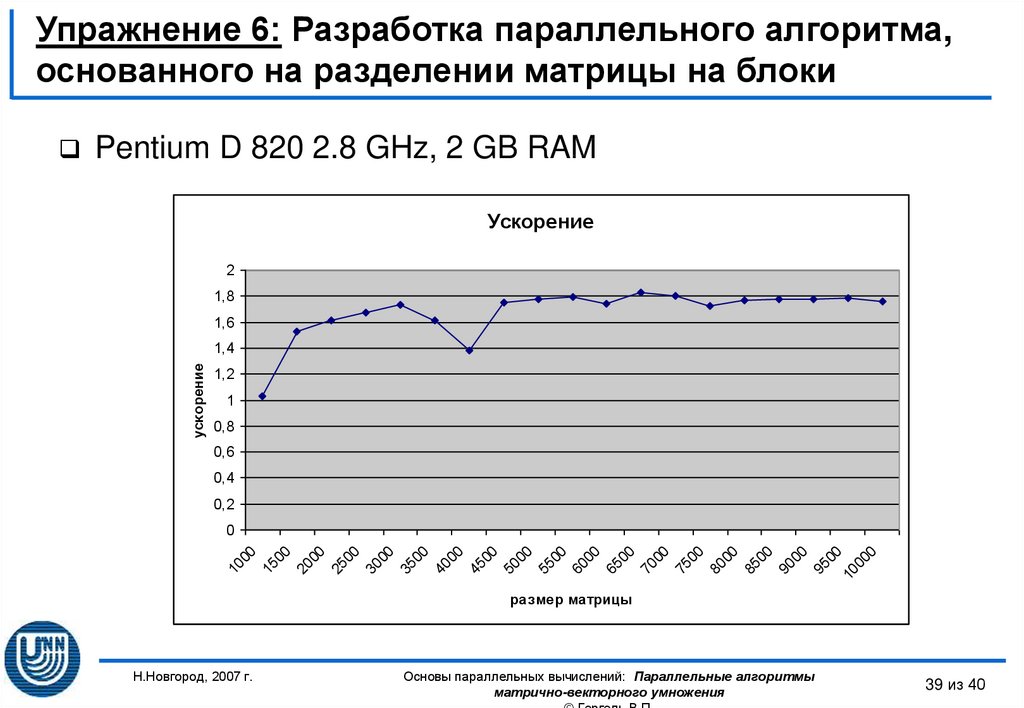
39. Упражнение 6: Разработка параллельного алгоритма, основанного на разделении матрицы на блоки
Pentium D 820 2.8 GHz, 2 GB RAMУскорение
2
1,8
1,6
1,4
ускорение
1,2
1
0,8
0,6
0,4
0,2
0
10
00
15
00
20
00
25
00
30
00
35
00
40
00
45
00
50
00
55
00
60
00
65
00
70
00
75
00
80
00
85
00
90
00
95
00
10
00
0
размер матрицы
Н.Новгород, 2007 г.
Основы параллельных вычислений: Параллельные алгоритмы
матрично-векторного умножения
39 из 40
40. Заключение
Рассмотрен три метода параллельного выполненияумножения матрицы на вектор
Разработаны приложения, реализующие последовательный и
параллельные алгоритмы умножения матрицы на вектор
Проведены вычислительные эксперименты, проведено
сравнение последовательного и параллельного алгоритмов
Н.Новгород, 2007 г.
Основы параллельных вычислений: Параллельные алгоритмы
матрично-векторного умножения
40 из 40
















 Программирование
Программирование








