Метод бесконечного спуска. Решение задач с конечными множествами

1.

Метод бесконечного
спуска
Как бесконечное помогает в
решении задач с конечными
множествами
Работу подготовила
ученица 8 «Е» класса
гимназии №12
Чернухина Полина

2.

Цель: проанализировать возможности метода бесконечного
спуска в решении нетривиальных задач.
Задачи:
- Показать возможности метода на примере решения
важнейших задач школьной алгебры.
- Обосновать логическую эквивалентность трёх утверждений:
принципа бесконечного спуска, принципа наименьшего
элемента и принципа математической индукции.
- Обобщить метод бесконечного спуска на случай
трансфинитных порядковых чисел (ординалов).
- Показать возможности метода бесконечного спуска,
обобщённого на случай ординалов, на примере решения
нетривиальной задачи.
2

3. Простейшая формулировка принципа бесконечного спуска:

Не существует бесконечной убывающей
последовательности из натуральных чисел.
¬∃x ∀y∈x ∃z∈x (z˂y),
где x ⸦ N (множество натуральных
чисел), y ∈ N, z ∈ N
4

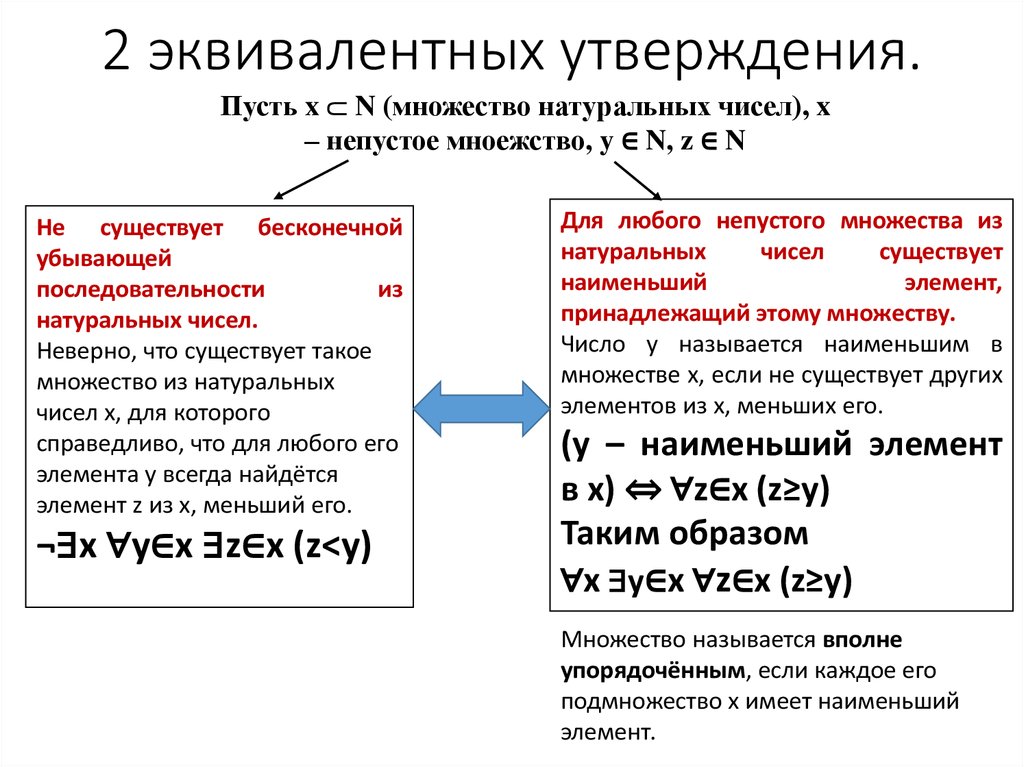
4. 2 эквивалентных утверждения.

Пусть x ⸦ N (множество натуральных чисел), x
– непустое мноежство, y ∈ N, z ∈ N
Не существует бесконечной
убывающей
последовательности
из
натуральных чисел.
Неверно, что существует такое
множество из натуральных
чисел х, для которого
справедливо, что для любого его
элемента у всегда найдётся
элемент z из х, меньший его.
¬∃x ∀y∈x ∃z∈x (z˂y)
Для любого непустого множества из
натуральных
чисел
существует
наименьший
элемент,
принадлежащий этому множеству.
Число у называется наименьшим в
множестве x, если не существует других
элементов из х, меньших его.
(y – наименьший элемент
в х) ⇔ ∀z∈x (z≥y)
Таким образом
∀х ∃y∈x ∀z∈x (z≥y)
Множество называется вполне
упорядочённым, если каждое его
подмножество х имеет наименьший
элемент.

5.

Пошаговый протокол доказательства
эквивалентности утверждений
Пусть х – непустое подмножество натуральных чисел.
Принцип наименьшего элемента
Закон двойного отрицания: ¬ ¬A ⇔A
∀х ∃y∈x ∀z∈x (z≥y)
¬ ¬ ∀х ∃y∈x ∀z∈x (z≥y)
Закон де Моргана
¬ ∃х¬ ∃y∈x ∀z∈x (z≥y)
Закон де Моргана
¬ ∃х ∀y∈x ¬∀z∈x (z≥y)
Закон де Моргана
¬ ∃х ∀y∈x ∃z∈x ¬(z≥y)
¬z≥y ⇔ z˂y
Принцип бесконечного спуска
¬∃x ∀y∈x ∃z∈x (z˂y)
¬∃x ∀y∈x ∃z∈x (z˂y)

6. Принцип математической индукции логически эквивалентен (равносилен) принцип наименьшего числа

I. Докажем, что из принципа
наименьшего числа следует принцип
математической индукции. Проведём
доказательство от противного. Пусть для
натуральных чисел верен принцип
наименьшего числа (мы, например,
примем его за исходную аксиому), и для
некоторого утверждения А верно А(1). И
пусть верно утверждение, что если
верно А(k), то и верно А(k+1).
Предположим, что утверждение
некоторое A(n) верно не при любых
натуральных n (принцип МИ не
выполняется). Рассмотрим множество
тех чисел, для которых оно неверно. В
нем есть наименьшее число N. Это
число не равно 1, так как A(1) истинно.
Но тогда A(N − 1) истинно по выбору N.
Значит, и A(N) = A(N − 1 + 1) истинно.
Пришли к противоречию.
II. Докажем принцип наименьшего числа логически
следует из принципа МИ.
Пусть верен принцип математической индукции, но
СУЩЕСТВУЕТ некоторое НЕПУСТОЕ множество X ⊆ N, в
котором нет наименьшего числа.
С помощью метода математической индукции мы
докажем, что это множество все же ПУСТОЕ, тем самым
придя к противоречию.
Докажем, что не существует натурального числа,
принадлежащего Х методом МИ.
Возьмём в качестве утверждения А(n), зависящего от
натуральной переменной: «Неверно, что n∊X»
Базис индукции. Число 1 не принадлежит Х A(1) (так как
меньше нуля чисел нет).
Шаг индукции. Делаем индукционное предположение:
Если число k не принадлежит Х, то k+1 тоже не
принадлежит Х.
В этом случае все числа, меньшие k и само число k
множеству Х не принадлежат.
Если бы число k+1 принадлежало бы множеству Х, то оно
было бы НАИМЕНЬШИМ.

7.

• Историческая справка.
• Метод бесконечного спуска изобрели, по-видимому,
древнегреческие математики.
• Метод бесконечного спуска был существенно развит
Пьером Ферма. Есть основания полагать, что Ферма
пытался доказывать свою Великую теорему именно этим
методом.
Пьер Ферма (1607-1665) французский
математик-самоучка
7

8.

В школьном учебнике мы доказываем
лишь множество частных случаев.
Доказать иррациональность корня из двух
Стр. 113

9.

ОДНАКО СУЩЕСТВУЕТ
ОДНО ОБЩЕЕ
УТВЕРЖДЕНИЕ,
КОТОРОЕ МОЖНО
ЛЕГКО ДОКАЗАТЬ С
ПОМОЩЬЮ МЕТОДА
БЕСКОНЕЧНОГО
СПУСКА (МБС).

10. Теорема: Корень квадратный любого натурального числа является или натуральным, или иррациональным

Доказательство:
1. Рациональное число можно представить отношением двух
целых чисел.
А
2. Пусть N – натуральное число, В - отношение двух
натуральных чисел, где B 1.
А
3. √N= В
2
А
N= 2
В

11.

ВхN
А
=
А
В
Две дроби равны тогда и только тогда, когда равны их целые и дробные части.
Например, дроби 10/3 и 20/6 равны, при этом 10/3=31/3, а 20/6=32/6
Что такое дробная часть в дроби
ВхN ?
А
Это то какая-то дробь А1/А, где А1 должно быть меньше A
4. А1
В1
=
, где А1˂А, В1˂В (равенство дробных частей).
В
А
А1
А
=
В
В1

12. Геркулес и гидра

13. Что такое гидра?

• Гидра - любое конечное дерево,
растущее из одного корня.
• Количество "сыновей" каждой
вершины конечно.
• Головами гидры назовём
вершины, не имеющие
сыновей. В данном примере
головы - B,D,F,G,H.

14. Как головы отрубают, и как они отрастают?

• Геркулес отрубает одну из голов
гидры.
• Если у отрубленной головы нет
"дедушки",
то
ничего
не
происходит и мы переходим к
следующему ходу.

15.

А
А
В
В
С
D
E
F G H
E2
С
D
E
F H
F2
E1
F1
H2
H1
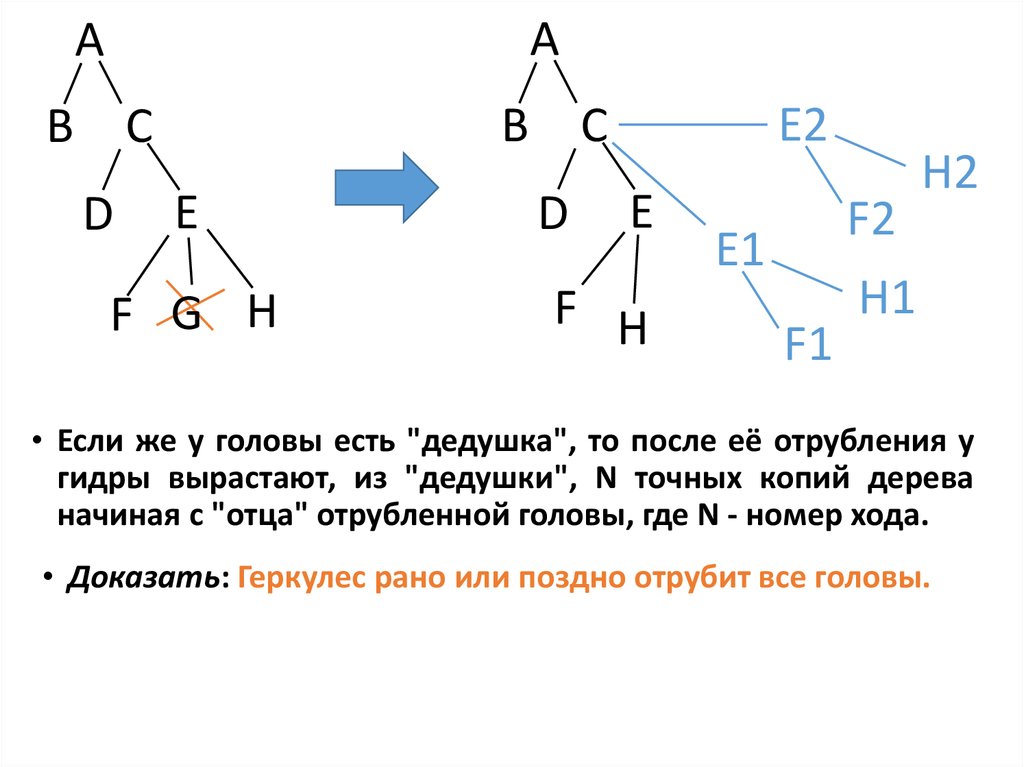
• Если же у головы есть "дедушка", то после её отрубления у
гидры вырастают, из "дедушки", N точных копий дерева
начиная с "отца" отрубленной головы, где N - номер хода.
• Доказать: Геркулес рано или поздно отрубит все головы.

16.

На 3 ходу

17. Гипотеза

• 1. Гидра не способна
расти вверх (увеличивать
высоту дерева). Жалко
её.
• 2. Рано или поздно возникнет ситуация, когда
останется только корень и куча голов идущих от
него. И не важно, что голов может быть НУ ОЧЕНЬ
МНОГО, но все равно конечное количество.
• 3. При достижение пункта 2 гидра перестанет расти
вширь, превратится в «одуванчик» и рано или
поздно умрет.

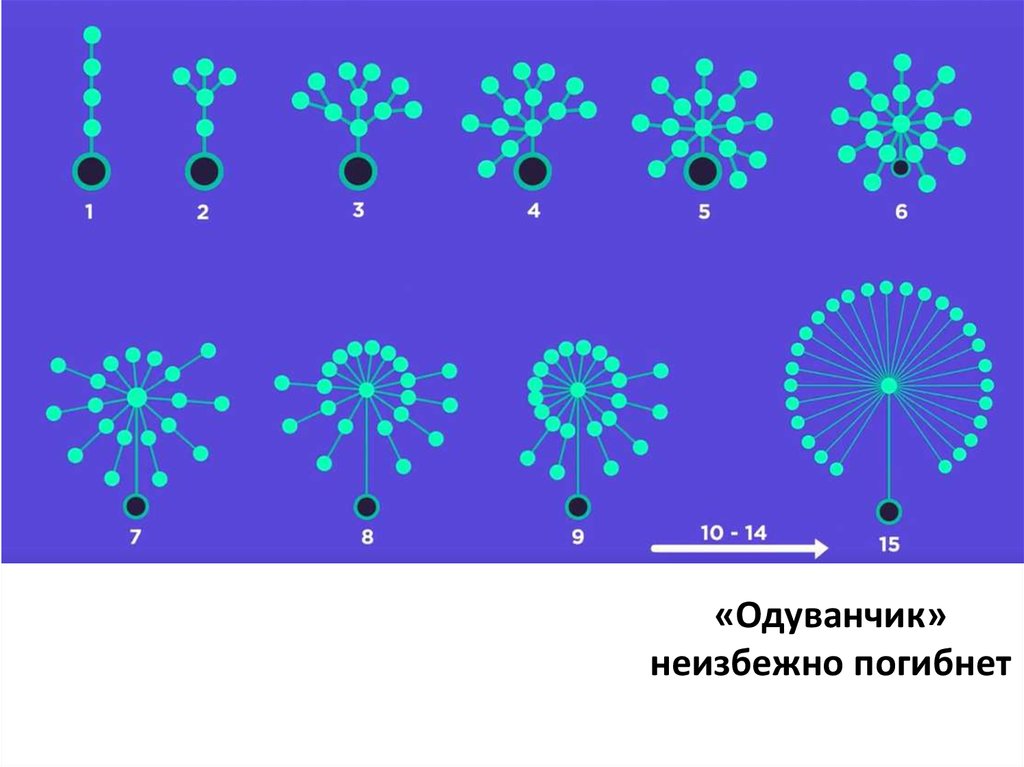
18.

«Одуванчик»
неизбежно погибнет

19.

• Красота задачи в том, что не смотря на простое
условие, она требует для решения каких-то
новых на первый взгляд не связанных с этой
задачей математических абстракций.
• И этой новой абстракцией будет ОРДИНАЛ.

20. Натуральные числа отвечают на два РАЗНЫХ вопроса:

• Сколько? - Это количество.
У меня есть 10 ВКУСНЫХ булочек.
• Который по счёту?

21. Натуральные числа как указатели порядка.

22. Ординалы – обобщения порядковых чисел.

• Ординалы представляют собой
обобщение понятия порядковых
натуральных чисел.
• Как и другие разновидности чисел, их
можно складывать, перемножать и
возводить в степень.
• Порядковые числа были введены
Георгом Кантором в 1883 году.
1845-1918
Георг Кантор –
основатель теории
бесконечных
множеств

23. В основу конструирования ординалов я положила высказывание Г.Кантора

«Множество есть
совокупность элементов,
мыслимых как единое целое»

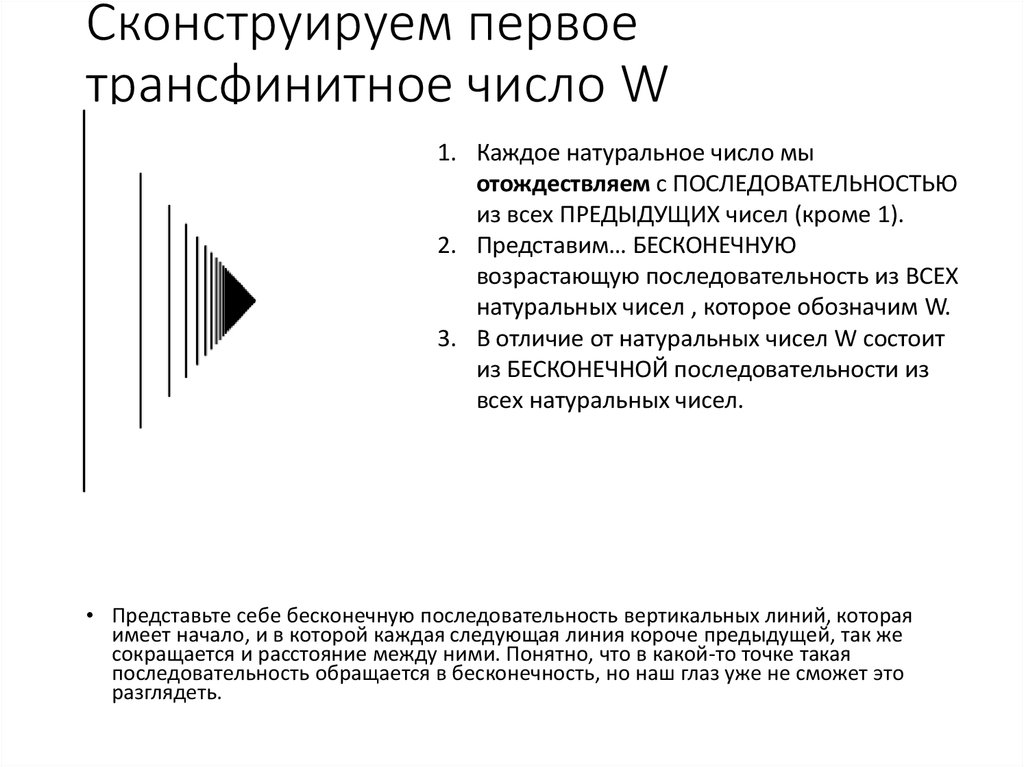
24. Сконструируем первое трансфинитное число W

1. Каждое натуральное число мы
отождествляем с ПОСЛЕДОВАТЕЛЬНОСТЬЮ
из всех ПРЕДЫДУЩИХ чисел (кроме 1).
2. Представим… БЕСКОНЕЧНУЮ
возрастающую последовательность из ВСЕХ
натуральных чисел , которое обозначим W.
3. В отличие от натуральных чисел W состоит
из БЕСКОНЕЧНОЙ последовательности из
всех натуральных чисел.
• Представьте себе бесконечную последовательность вертикальных линий, которая
имеет начало, и в которой каждая следующая линия короче предыдущей, так же
сокращается и расстояние между ними. Понятно, что в какой-то точке такая
последовательность обращается в бесконечность, но наш глаз уже не сможет это
разглядеть.

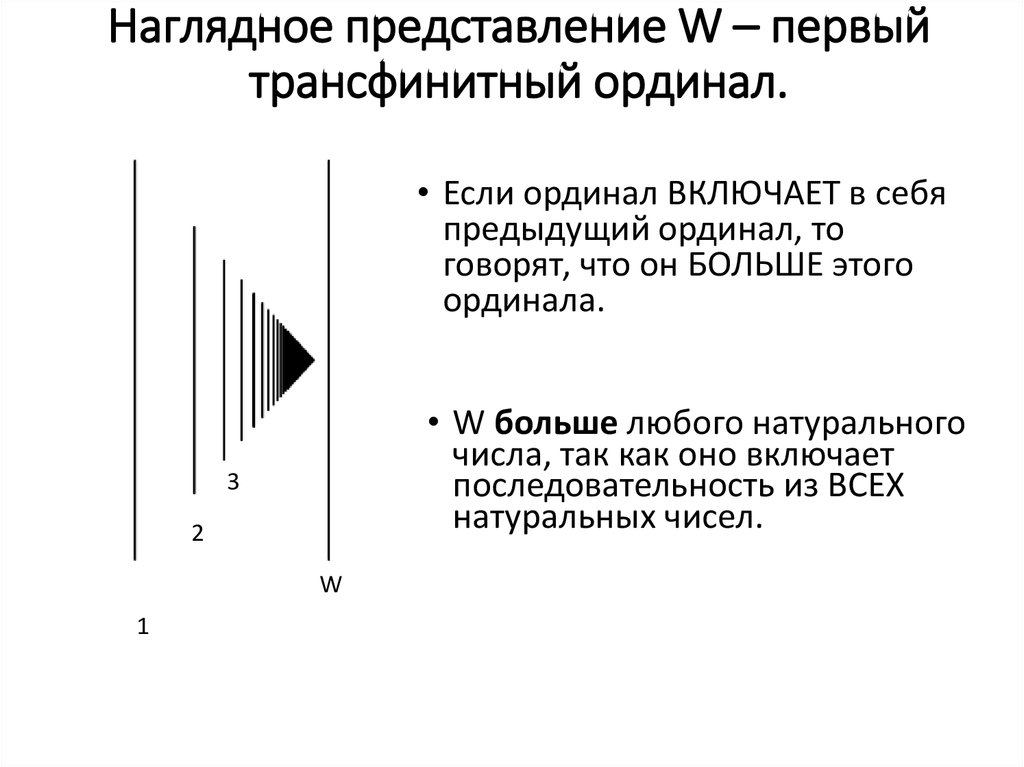
25. Наглядное представление W – первый трансфинитный ординал.

• Если ординал ВКЛЮЧАЕТ в себя
предыдущий ординал, то
говорят, что он БОЛЬШЕ этого
ординала.
• W больше любого натурального
числа, так как оно включает
последовательность из ВСЕХ
натуральных чисел.
3
2
W
1

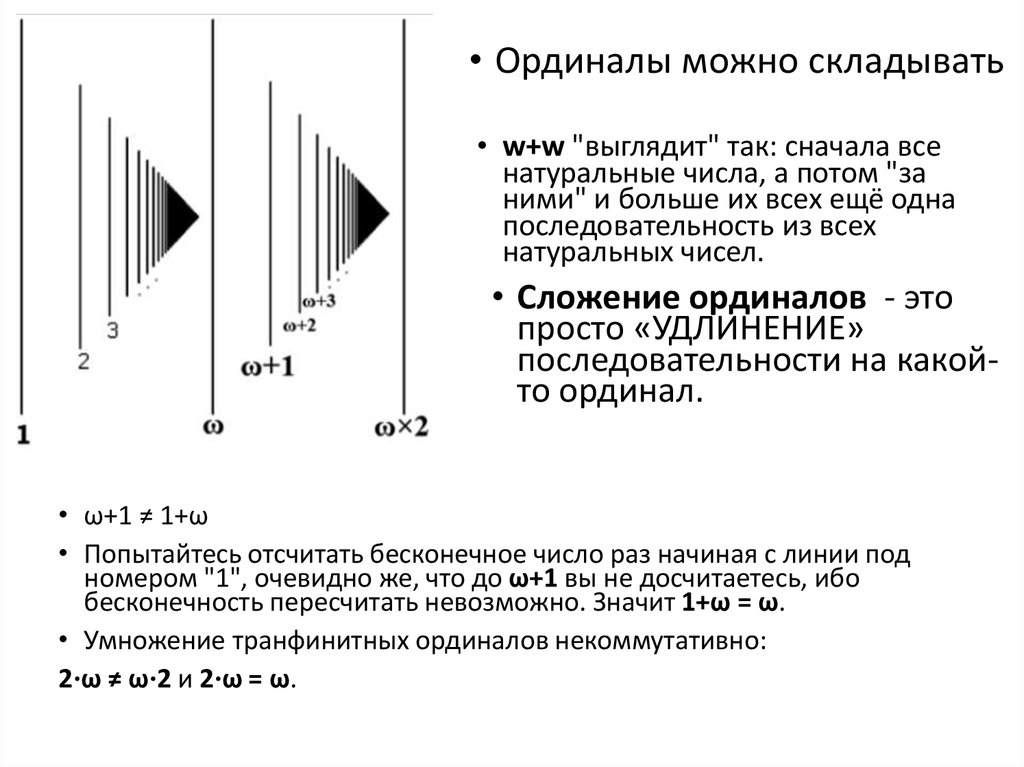
26.

• Ординалы можно складывать
• w+w "выглядит" так: сначала все
натуральные числа, а потом "за
ними" и больше их всех ещё одна
последовательность из всех
натуральных чисел.
• Сложение ординалов - это
просто «УДЛИНЕНИЕ»
последовательности на какойто ординал.
• ω+1 ≠ 1+ω
• Попытайтесь отсчитать бесконечное число раз начиная с линии под
номером "1", очевидно же, что до ω+1 вы не досчитаетесь, ибо
бесконечность пересчитать невозможно. Значит 1+ω = ω.
• Умножение транфинитных ординалов некоммутативно:
2⋅ω ≠ ω⋅2 и 2⋅ω = ω.

27. Повторим принцип определения.

• 1 – это ПЕРВОЕ натуральное число.
• 3 – это ПОСЛЕДОВАТЕЛЬНОСТЬ из двух предыдущих
натуральных чисел: 1 и 2
• W – это ПОСЛЕДОВАТЕЛЬНОСТЬ из ВСЕХ
натуральных чисел.
• W+1 – это последовательность из всех натуральных
чисел и следующего за ними W
• W+2 – это последовательность из всех натуральных
чисел и следующих за ними W и W+1
• W+W – это последовательность, включающая все
натуральные числа и все трансфинитные числа вида
W+N, где N – натуральное число

28. Выстроим w последовательностей из W

Операция первого уровня:
Если мы операцию умножения W на
W применим 2 раза,
то получим W2+1=W3
Важная формула:
Wх+1=WхxW
Операция второго уровня:
Если мы ОПЕРАЦИЮ умножения
W на W повторим W раз,
то получим WW
W2=
«БЕЗУМНАЯ» ИДЕЯ!!!
Операция третьего уровня:
Если мы ОПЕРАЦИЮ возведения
W в степень W раз повторим W
раз, то получим ….

29. Наглядное изображение W2

• W х W=W2 – это бесконечная W последовательность ординалов W.

30.

Не для всех ординалов можно указать непосредственно предыдущий, но для
каждого ординала можно указать непосредственно следующий за ним.
Поэтому, например, рациональные
числа НЕ ординалы.

31.

• Итак, мы можем w умножить на W W раз, и
повторить эту процедуру W раз. Это будет WW.
• Саму же последнюю процедуру повторения
возведения в степень W мы повторим W раз.
• В итоге получим «жутко большой» ординал
…
W
W
W
W
W
W раз
ε0
• Мы получили ординал эпсилон-ноль - ε0. От
него тоже можно продолжать дальше и строить,
скажем, ε0+1 и т.п., но для решения задачи это
уже не нужно.

32. Важные свойства построенных ординалов

• Начиная с w, можно складывать, умножать и
возводить в степень друг друга сколько угодно
раз, и никогда не выйдешь за пределы ε0.
• Для всех этих ординалов, включая
ε0, справедлив принцип бесконечного спуска.

33. Продвинутая формулировка метода бесконечного спуска основана на фундаментальном факте:

Не существует бесконечной убывающей
последовательности из ординалов.

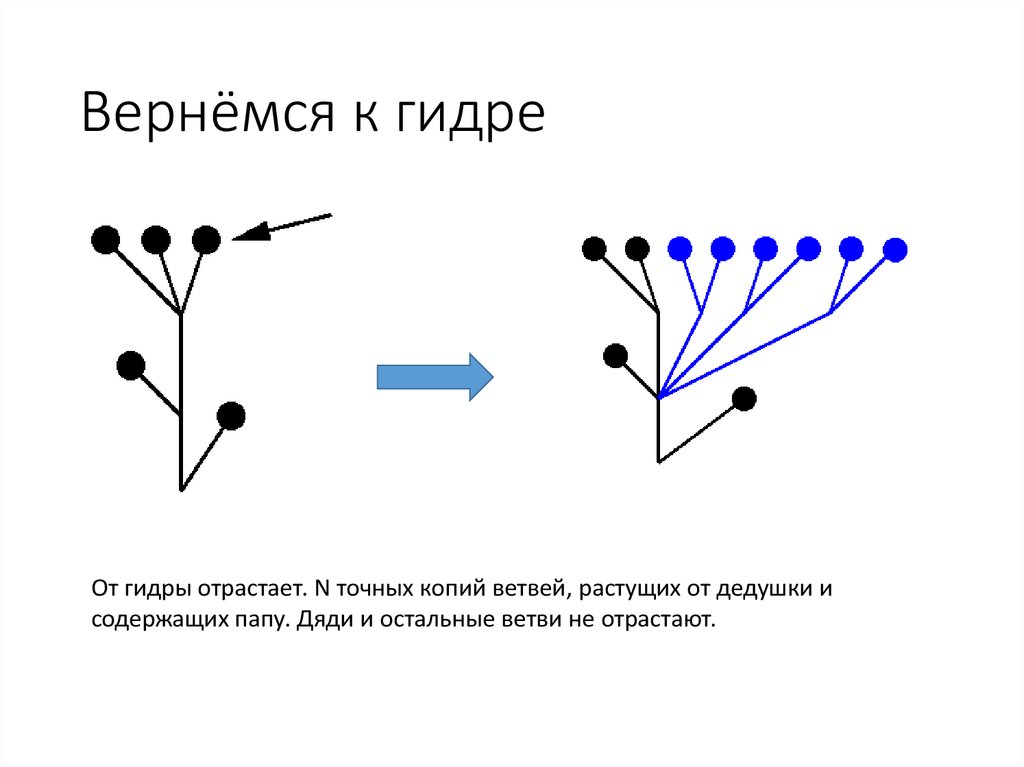
34. Вернёмся к гидре

От гидры отрастает. N точных копий ветвей, растущих от дедушки и
содержащих папу. Дяди и остальные ветви не отрастают.

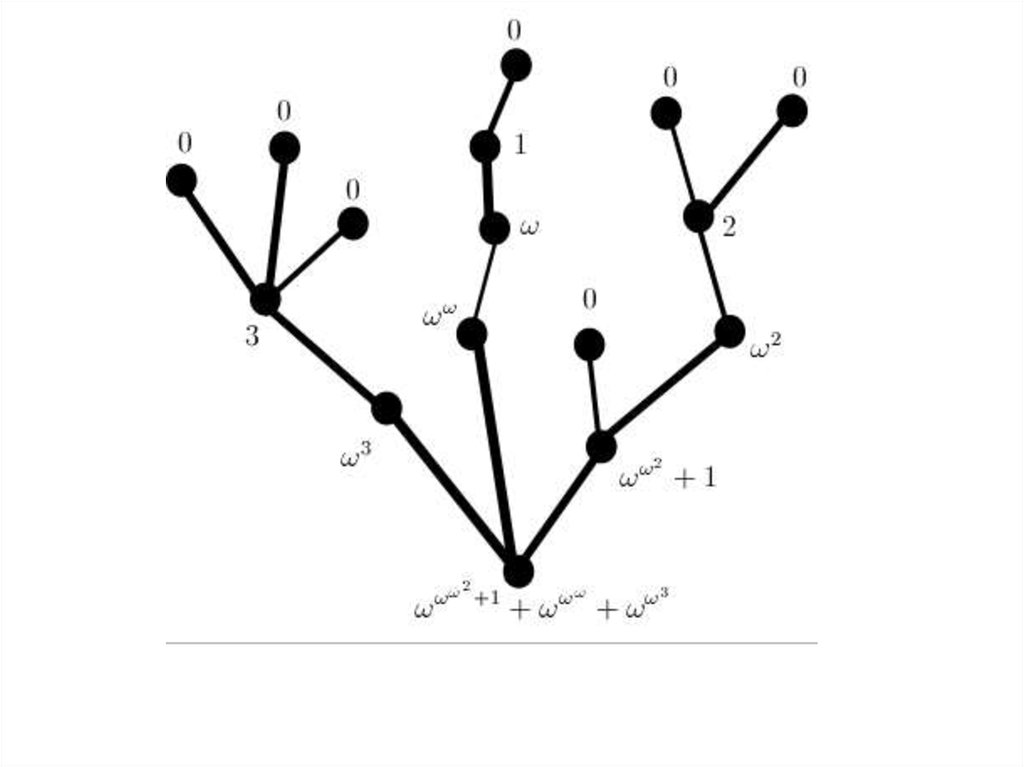
35. Каждой гидре сопоставим ординал

• Каждая голова гидры
получает значение 0.

36.

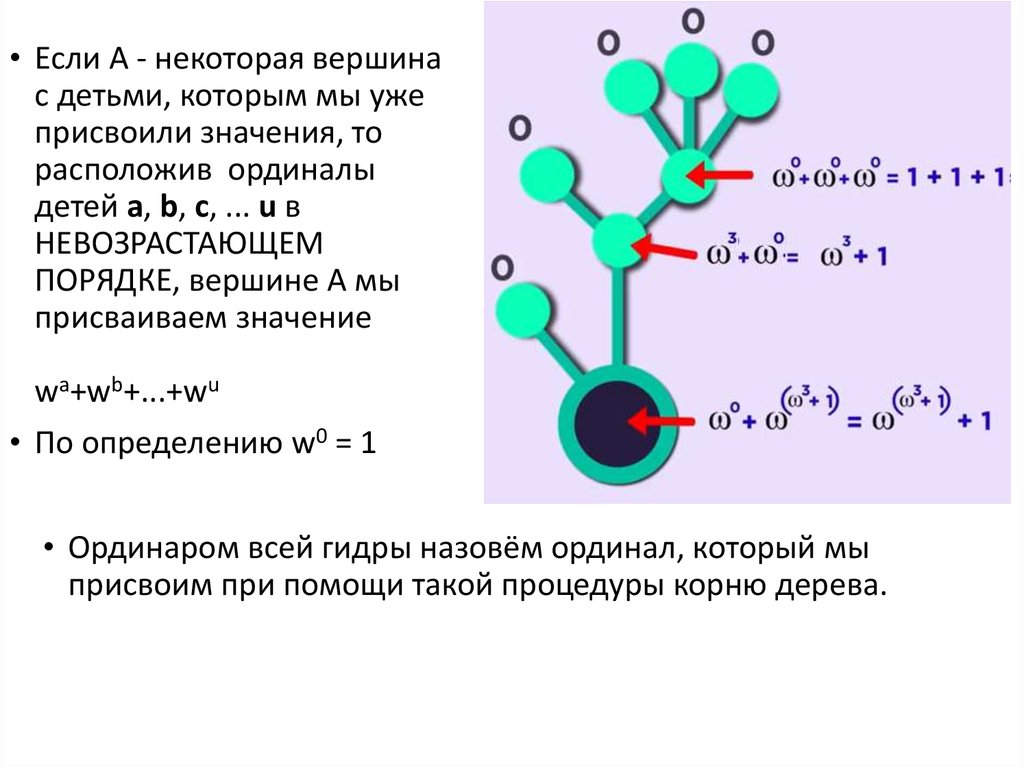
• Если A - некоторая вершина
с детьми, которым мы уже
присвоили значения, то
расположив ординалы
детей a, b, c, ... u в
НЕВОЗРАСТАЮЩЕМ
ПОРЯДКЕ, вершине A мы
присваиваем значение
wa+wb+...+wu
• По определению w0 = 1
• Ординаром всей гидры назовём ординал, который мы
присвоим при помощи такой процедуры корню дерева.

37.

38.

Лемма: после каждого хода Геркулеса ординал гидры
уменьшается. То есть, если On - ординал гидры после nго хода, то On+1 < On (неравенство точное!).
Доказательство:
• Достаточно доказать, что после каждого хода
ординал дедушки отсечённой головы
уменьшается.
• Можно игнорировать существующих до
отсечения "дядей" отсекаемой головы - их вклад
в "дедушку" до и после отсечения не меняется.

39.

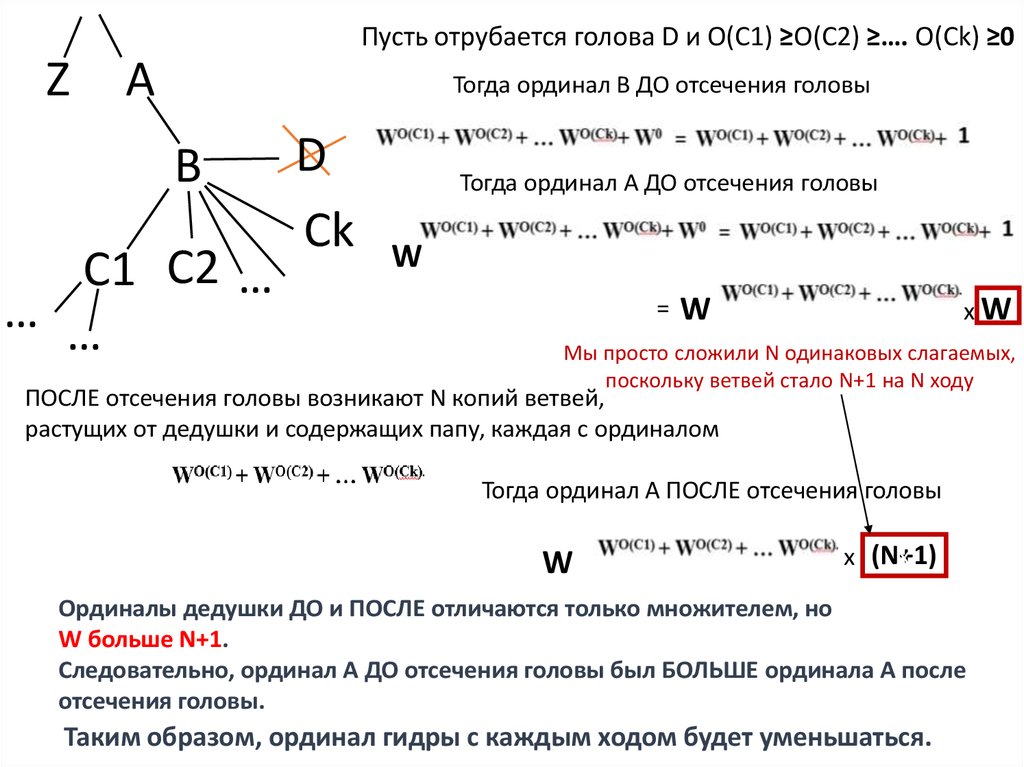
Пусть отрубается голова D и О(С1) ≥О(С2) ≥…. О(Сk) ≥0
Z
А
Тогда ординал В ДО отсечения головы
B
C1 C2 …
… …
D
Ck
Тогда ординал А ДО отсечения головы
W
=
W
хW
Мы просто сложили N одинаковых слагаемых,
поскольку ветвей стало N+1 на N ходу
ПОСЛЕ отсечения головы возникают N копий ветвей,
растущих от дедушки и содержащих папу, каждая с ординалом
Тогда ординал А ПОСЛЕ отсечения головы
W
х
х (N+1)
Ординалы дедушки ДО и ПОСЛЕ отличаются только множителем, но
W больше N+1.
Следовательно, ординал А ДО отсечения головы был БОЛЬШЕ ординала А после
отсечения головы.
Таким образом, ординал гидры с каждым ходом будет уменьшаться.

40. Выводы.

1. Метод бесконечного спуска (МБС) – это способ
доказательства, позволяющий доказывать множество утверждений,
например, иррациональность квадратного корня из натуральных чисел.
2. Доказана логическая эквивалентность трёх утверждений:
принципа бесконечного спуска, принципа наименьшего элемента и
принципа математической индукции.
3. С помощью МБС приведено доказательство утверждения о
том, что корень квадратный из натурального числа или натуральный,
или иррациональный.
4. Натуральные числа могут служить как для обозначения
количества, так и для обозначения порядкового номера. В качестве
порядковых чисел их можно обобщить на случай бесконечных вполне
упорядочённых множеств - ординалов.
5. Для ординалов не существует бесконечной убывающей
последовательности, поэтому их можно использовать для
доказательства утверждений с помощью МБС.
6. Ординалы позволяют решать ряд, казалось бы, несложно
сформулированных задач, которые, однако, не могут быть решены
только применением натуральных чисел: в работе подробно
рассмотрена одна такая задача – «Геркулес и Гидра».

41.

Литература
1. Густаво Эрнесто Пинейро Бесчисленное поддается подсчету.
Кантор. Бесконечность в математике. / Пер. с итал. — М: Де Агостини, 2015. —
168 с.
2. И. В. Ященко Парадоксы теории множеств.
https://www.mccme.ru/mmmflectures/books/books/books.php?book=20&page=11\
3. Николай Вавилов «Не совсем наивная теория множеств». Лекции
в ЛГУ.
Интернет-источники
1. Mark Kim-Mulgrew Killing the hydra. /
https://markkm.com/blog/killing-the-hydra/
2. https://johncarlosbaez.wordpress.com/2016/06/29/large-countableordinals-part-1/
3. https://www.slideserve.com/abdul-simpson/by-rudolf-fleischerfudan-university
4.
https://digitalccbeta.coloradocollege.edu/pid/coccc:11178/datastream/OBJ
5. https://www.quora.com/Has-anyone-found-more-interestingpropositions-that-cannot-be-proven-true-or-false-based-on-the-discovery-ofG%C3%B6del
6. https://www.youtube.com/watch?v=K1XSZdXydRE

42.

• 1. Когда вводятся ординалы, то вместо сложения возникает прибавление
справа и прибавление слева, это две разные операции. w+1 - новое число,
но 1+w = w.
2. Вычитание - это операция, обратная к сложению. Соответственно, есть
два вычитания - обратное к прибавлению слева (левое вычитание) и
обратное к прибавлению справа (правое вычитание).
Левый случай: w-1 - это ординал X такой, что 1+X=w. Понятно, что X=w.
Правый случйй: w-1 - ординал X такой, что Х+1=w. Давайте докажем, что
такого X не бывает. Действительно, на не являющихся конечными
ординалах задано отношение порядка, и w - минимальный элемент
(существует, ибо лемма Цорна). Но Х должен быть меньше w, значит, он
конечен. Но после прибавления 1 к конечному числу получается снова
конечное, значит, такого Х не существует.
Т.е., нельзя вычитать из ординала справа 1, как делить на 0. Ничего не
получится. Т.е., можно попробовать, но контекст (частичная
упорядоченность + вера в аксиому выбора) рухнет.