Похожие презентации:
Моделирование сферы потребления
1. Тема 2. Моделирование сферы потребления
2.1. Моделирование на микроуровне:2.1.1. Функции полезности и кривые
безразличия.
2.1.2. Задача потребительского выбора и
ее практическое применение.
2.2. Макроэкономические функции
потребления и их свойства
2. 2.1. Моделирование на микроуровне
2.1.1. Функции полезности и кривыебезразличия.
2.1.2. Задача потребительского выбора и
ее практическое применение.
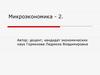
3. Цель моделирования
Цель моделирования сферы потребления намикроуровне – изучение механизма выбора
потребителем различных благ на рынках товаров и
услуг, т.е. изучение механизма формирования
рыночного спроса.
Основная модель – модель потребительского выбора:
.
4. 2.1.1. Функции полезности и кривые безразличия
5. Функция полезности
Функция полезности потребителя - количественнаяоценка набора благ со стороны потребителя, функция
вида
Функция полезности отражает отношение между
объемами потребляемых товаров и услуг и уровнем
полезности, достигаемым потребителем.
Эта функция удовлетворяет условиям:
1. Если x предпочтительнее y, то u (x) > u (y).
2. Если x и y равноценны, то u (x) = u (y).
6. Функция полезности
Предельная полезность i - го вида благадополнительная полезность, которую получит
потребитель от потребления каждой дополнительной
единицы блага данного вида.
7. Функция полезности
Свойства функции полезности:1. C увеличением потребления какого либо блага значение
функции полезности потребителя возрастает:
2. C увеличением объема потребления какого либо блага
предельная полезность данного вида блага убывает (закон
Госсена):
3. Если с увеличением потребления i-го вида блага увеличивается
потребление j-го блага, то предельная полезность i-го вида блага
увеличивается:
8. Функция полезности
Виды функций полезности:1. Функция полезности для совершенных товарозаменителей:
2. Функция полезности с полным дополнением благ
3. Неоклассическая функция полезности
9. Кривые безразличия
x2A
x2 A
x2 B
C
B
u3
u2
u1
0
x1 A x1 B
x1
Кривая безразличия
- множество наборов
благ, обеспечивающих
потребителю
заданный уровень
полезности:
u (x1, x2) = const
10. 2.1.2. Задача потребительского выбора и ее практическое применение
11. Формулировка задачи
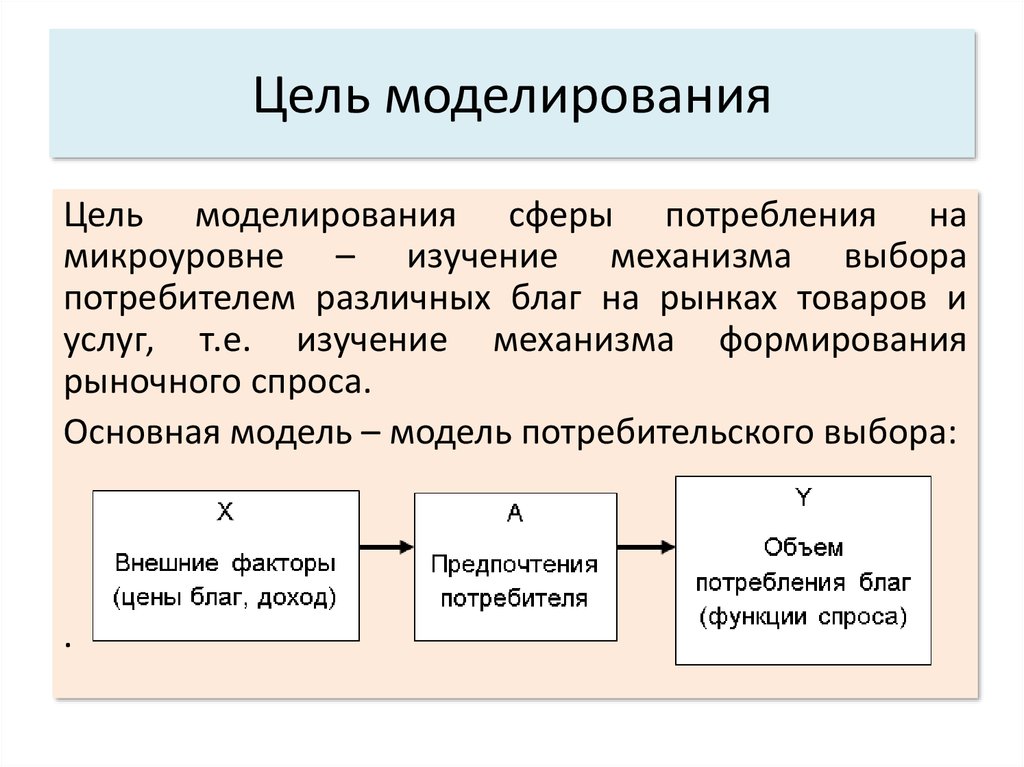
Cреди множества наборов благ, доступныхпотребителю, потребитель стремится выбрать
тот, который обеспечит ему наибольший
уровень полезности.
12. Графическая иллюстрация для двух благ
.x2
x2 E
E
u3
u2
u1
0
x1 E
x1
13. Математическая формулировка
I - размер дохода потребителяx1, … , xn – количества благ
p1, … , pn - цены единиц благ
- бюджетное множество потребителя
n
px
i 1
i i
I
- бюджетная линия
14. Математическая формулировка
u ( x1 ,..., x n ) maxn
px
i 1
i
i
I
Это задача нелинейного программирования.
15. Решение задачи
Функция Лагранжа:Условие максимума функции Лагранжа: равенство всех
частных производных 0. То есть:
16. Условия решения задачи
MU ipi
, i 1,..., n
MU j p j
n
px
i 1
i i
I
17. Функции спроса Маршалла
Решение задачи потребительского выбора можно записать ввиде функций спроса Маршалла:
x1* M 1 ( p1 ,..., pn , I )
x M 2 ( p1 ,..., pn , I )
*
2
...
xn* M n ( pn ,..., pn , I )
18. Практическое применение модели потребительского выбора
Модель потребительского выбора позволяетполучить функции спроса на отдельные блага.
Исследование свойств этих функций является
основой
для
изучения
характеристик
потребительского спроса при разработке
маркетинговой политики фирмы.
Основной
инструмент:
коэффициенты
эластичности.
19. Прямая эластичность спроса по цене
Прямая эластичность спроса по ценехарактеризует относительное изменение
объема спроса на i-тый товар при изменении
его цены на 1 процент.
20. Прямая эластичность спроса по цене
Точечная эластичностьхарактеризует
относительное изменение объема спроса при
бесконечно малом изменении цены:
или
21. Прямая эластичность спроса по цене
PP1
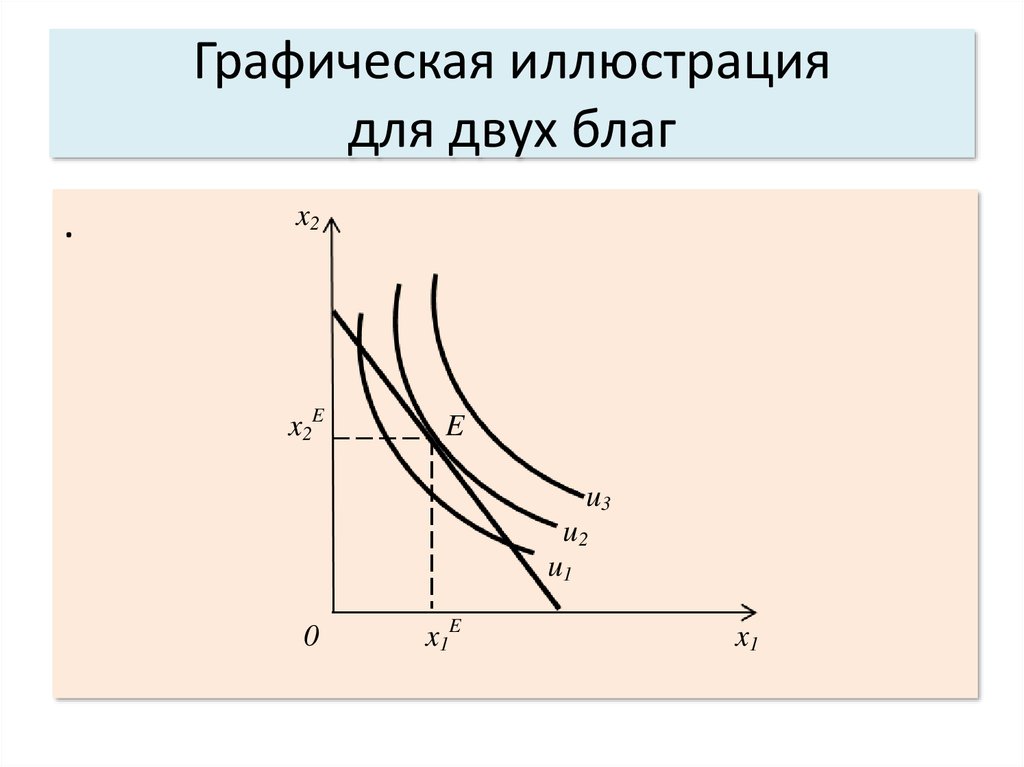
Дуговая
эластичность
характеризует
относительное
изменение
объема спроса при значительном
изменении
цены:
A
.M
P2
0
B
Q1
Q2
D
Q
.
22. Перекрёстная эластичность спроса по цене
Перекрестная эластичность спроса по ценехарактеризует относительное изменение
объема спроса на один товар при изменении
цены другого на 1 процент.
Коэффициент перекрестной эластичности:
23. Перекрёстная эластичность спроса по цене
Если Eij > 0, то товары i и j называютвзаимозаменяемыми, повышение цены j - того
товара ведет к увеличению спроса на i - тый.
Если Eij < 0, то товары i и j называют
взаимодополняющими, повышение цены j - того
товара ведет к падению спроса на i - тый.
Если Eij = 0, то такие товары называют
независимыми, повышение цены одного товара
не влияет на объем спроса на другой.
24. Эластичность спроса по доходу
Эластичность спроса по доходу характеризуетотносительное изменение спроса на какойлибо товар в результате изменения дохода
потребителя на 1 процент.
Коэффициент эластичности спроса по доходу:
25. Эластичность спроса по доходу
Если EI < 0, товар является низкокачественным,увеличение дохода сопровождается падением
спроса на этот товар.
Если EI > 0, товар называется нормальным , с
ростом дохода увеличивается и спрос на этот
товар.
Товары первой необходимости: 0 < EI < 1 - спрос
растет медленнее роста доходов и имеет предел
насыщения.
Предметы роскоши: EI > 1 - спрос опережает
рост доходов и не имеет предела насыщения.
26. 2.2. Макроэкономические функции потребления и их свойства
27. Цель моделирования
Цель моделирования сферы потребления на макроуровне:изучение механизма распределения созданного ВВП/ВНД
между различными макроэкономическими субъектами.
Потребление домашних хозяйств - сумма денежных
средств, которая тратится ими на приобретение товаров и
услуг, важнейший компонент совокупного спроса.
Основная модель – функция потребления:
.
28. Кейнсианская функция потребления
Потребление домашних хозяйств зависит отабсолютной величины текущего дохода.
В экономике без государства:
C = Ca + c * Y; Ca > 0; 0 < c < 1,
где Ca - величина автономного потребления;
c = ∆C/∆Y - предельная склонность
потреблению.
к
29. Кейнсианская функция потребления
В экономике с государством:C = Ca + cYD · YD; Ca > 0; 0 < cYD < 1
где YD = Y – t · Y + TR – располагаемый доход;
cYD = ∆C/∆YD - предельная склонность к
потреблению располагаемого дохода.
30. Кейнсианская функция потребления
.C
c, C /Y
C = Ca + c * Y
C/Y
Ca
c
Y
Функция потребления
Кейнса
Y
Средняя и предельная
склонность к потреблению
31. Функция потребления Модильяни (модель жизненного цикла)
Планы потребления индивида составляютсятаким образом, чтобы обеспечить равномерный
уровень потребления в течение жизни.
Упрощенный вариант модели
Тж - число лет жизни индивида
Тр – число лет работы индивида
yt - доход индивида в году t.
Так как
,
то годовой объем потребления:
.
32. Функция потребления Модильяни (модель жизненного цикла)
Расширенный вариант моделиТж - число лет жизни индивида
Тр – число лет работы индивида
Т – текущий момент времени
y - среднегодовой доход индивида
v – размер накопленного богатства.
Потребительские возможности индивида в течение
оставшейся жизни:
C · (Тж – Т) = v + (Тр – Т) · y
Годовой объем потребления:
.
33. Функция потребления Модильяни (модель жизненного цикла)
Если каждый индивид строит свое потреблениетаким образом, то совокупная функция
потребления похожа на индивидуальную:
.
где cV - предельная склонность к потреблению по
накопленному богатству;
cY - предельная склонность к потреблению по
доходу.
.
34. Функция потребления Фридмена (модель перманентного дохода)
Текущий доход есть сумма постоянного(перманентного)
и
временного
дохода.
Перманентный доход – доход, который, согласно
ожиданиям потребителя, сохранится в будущем.
Потребление
домохозяйств
зависит
от
перманентного дохода.
Пусть перманентный доход:
yp = y0 + α(y1 – y0) = αy1 + (1 - α)y0; 0 < α < 1.
Тогда потребление домохозяйств:
Ct = Ct (yp) = c · yp = c · α · yt + c · (1 – α) · yt-1.






























 Экономика
Экономика