Похожие презентации:
Основы автоматизации проектирования РЭА. Вычисления в MATLAB. Числовые массивы. (Лекция 2)
1. Основы автоматизации проектирования РЭА.
Версия 1.2 – 28.01.2016Основы автоматизации проектирования РЭА.
Лекция 2. Вычисления в MATLAB. Числовые массивы.
2.1) техническое обеспечение САПР;
2.2) вычисления в MATLAB;
2.3) числовые массивы;
2. Лекция 2. Вычисления в MATLAB. Числовые массивы :
2.1) техническое обеспечение САПР;2.2) вычисления в MATLAB;
2.3) числовые массивы, массивы символов.
Page 2
3. 2.1) Техническое обеспечение САПР
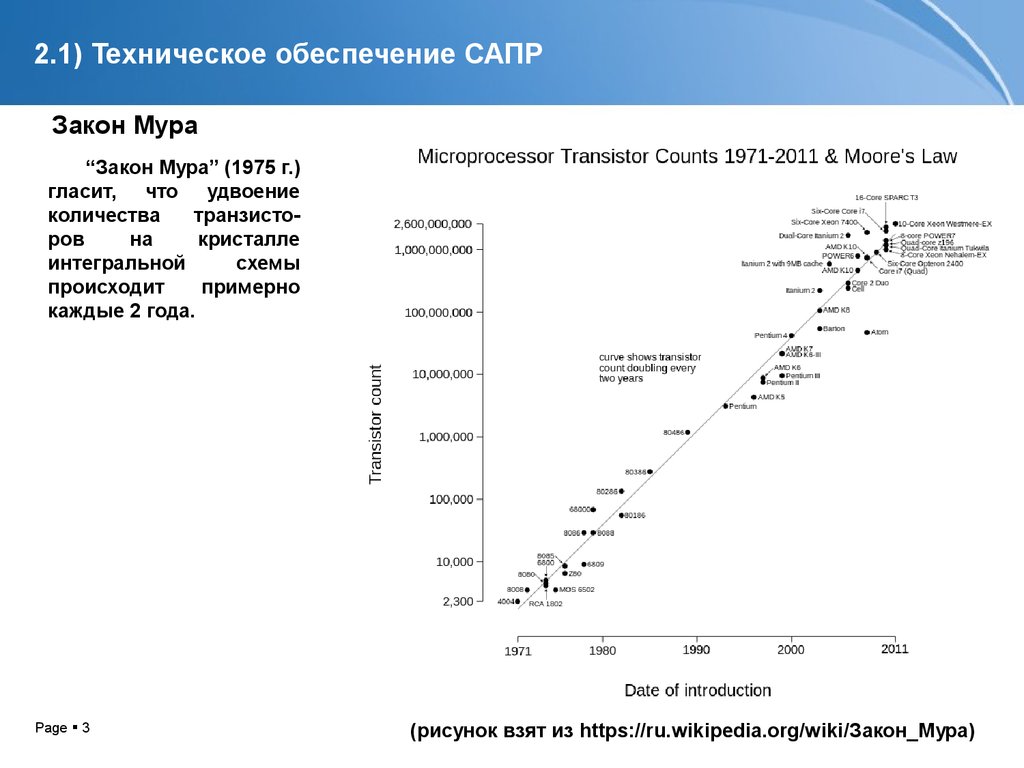
Закон Мура“Закон Мура” (1975 г.)
гласит, что удвоение
количества
транзисторов
на
кристалле
интегральной
схемы
происходит
примерно
каждые 2 года.
Page 3
(рисунок взят из https://ru.wikipedia.org/wiki/Закон_Мура)
4. 2.1) Техническое обеспечение САПР
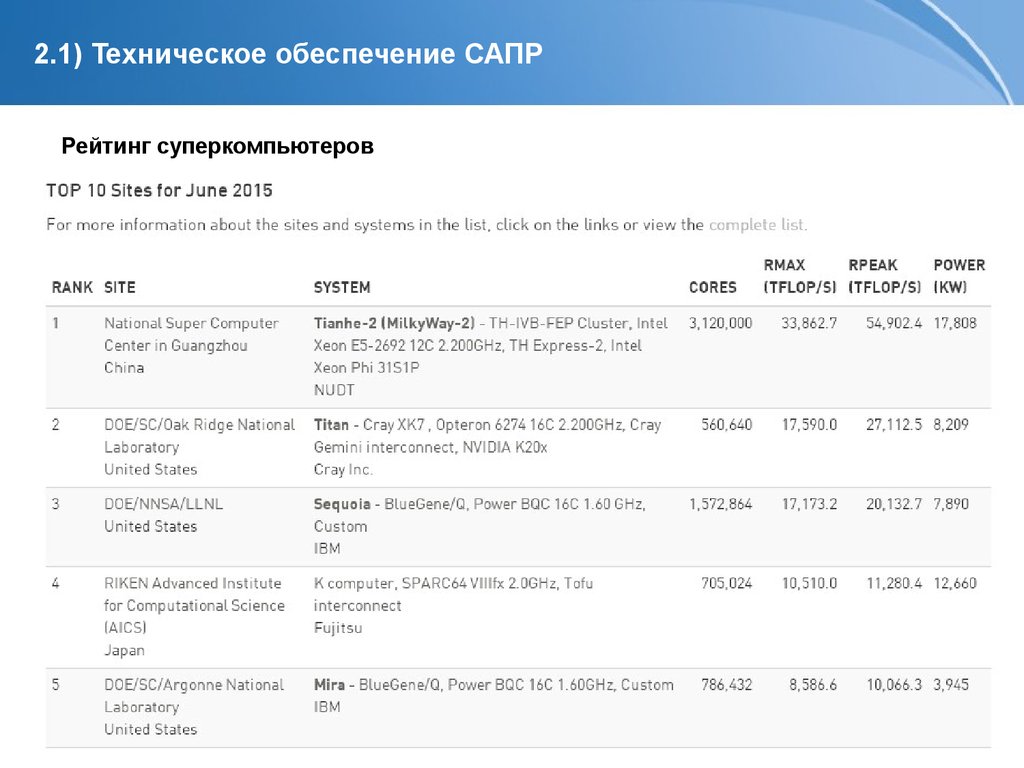
Рейтинг суперкомпьютеровPage 4
5. Лекция 2. Вычисления в MATLAB. Числовые массивы. :
2.1) техническое обеспечение САПР;2.2) вычисления в MATLAB;
2.3) числовые массивы, массивы символов.
Page 5
6. 2.2) Вычисления в MATLAB
1. Введение в проектированиеСистемные переменные:
i или j – мнимая единица;
• pi – 3.141592653589793e+000;
• eps – погрешность операций над числами с плавающей точкой,
eps = 2.220446049250313e-016;
• realmin – наименьшее число с плавающей точкой, realmin = 2.225073858507202e-308;
• realmax – наибольшее число с плавающей точкой, realmax = 1.797693134862316e+308;
• inf – значение машинной бесконечности;
• ans – переменная, хранящая результат последней операции;
• NaN – неопределенность, нечисловое значение (Not-a-Number), например 0/0.
Арифметические операции:
Page 6
7. 2.2) Вычисления в MATLAB
Формат отображения чисел в командном окне. Команда format <type>Основные допустимые значения для <type>.
• short – короткий формат (по умолчанию). Целая часть (по модулю) менее 1000, после запятой
содержит 4 знака, например x = 112.1416. Если модуль целой части больше 1000, то применяется
short e. Для целого числа отображается 9 знаков;
• short e – короткий формат числа с плавающей запятой с 5 знаками. Например, x = 1.1214e+002.
Для целого числа отображается 9 знаков;
• long – длинный формат, 16 знаков. Целая часть (по модулю) менее 100, остальные 14, или 15
знаков – после запятой, например 23.14069263277927. Если модуль целой части больше 100, то
применяется long e. Для целого числа отображается 9 знаков;
• long e – длинный формат числа с плавающей запятой с 16 знаками. Целая часть (по модулю)
менее 10, остальные 15 знаков – после запятой, например 2.314069263277927e+001. Для целого
числа отображается 9 знаков;
• rat – представление числа в виде рациональной дроби, например, pi = 355/113;
• hex – шестнадцатеричное представление числа с двойной точностью, например, pi =
400921fb54442d18.
Page 7
8. 2.2) Вычисления в MATLAB
Часто используемые функции:Для обработки чисел:
• round(x) – округление до ближайшего целого;
• fix(x) – обнуление всех знаков после запятой;
• floor(x) – целая часть числа, наибольшее целое, не
превосходящее данное x;
• ceil(x) – наименьшее целое, большее или равное x;
• sign(x) – знак числа, принимает значения -1, 0, +1;
• rem(x,y) – остаток от деления, x – n.*y, где n = fix(x./y)
Операторы сравнения:
< - меньше;
<= - меньше или равно;
> - больше;
>= - больше или равно;
== - равно тождественно;
~= - не равно.
Степенные функции:
exp
- экспонента
log
- натуральный логарифм
log10
- десятичный логарифм
log2
- двоичный логарифм.
pow2
- степень двойки.
sqrt
- квадратный корень.
Page 8
Для работы с комплексными числами :
• abs(z) – модуль комплексного числа, |z|;
• conj(z) – комплексно сопряженное число, a-bi;
• imag(z) – мнимая часть числа;
• real(z) – вещественная часть числа;
• angle(z) – аргумент числа;
• isreal(z) – дает логическую 1, если число
действительное и логический 0 – в случае
комплексного.
Логические операторы:
& - логическое И.
| - логическое ИЛИ.
~ - логическое НЕ.
Тригонометрические:
sin
- sinus.
sind
- Sine of argument in degrees.
sinh
- Hyperbolic sine.
asin
- Inverse sine.
asind
- Inverse sine, result in degrees.
asinh
- Inverse hyperbolic sine.
cos
- Cosine.
tan
- Tangent.
cot
- Cotangent.
sec
- Secant.
csc
- Cosecant.
Теория чисел:
factor
- умножение простыхчисел.
isprime - простое ли число.
primes
- список простых чисел.
gcd
- наибольший общийделитель.
lcm
- наименьшее общее кратное.
9. 2.2) Вычисления в MATLAB
Сценарии и функцииСценарии (программы)
Кода вы вызываете сценарий, MATLAB просто вызывает команды, содержащиеся в файле.
Сценарии могут оперировать существующими данными в рабочем пространстве или они могут сами
создавать эти данные. Хотя сценарии не возвращают значений, все переменные, которые они создают,
остаются в рабочем пространстве для использования в последующих вычислениях.
Пример программы
x = 2;
y = 3;
z=sqrt(x^2+y^2);
Функции
Функции - это М-файлы, которые могут иметь входные и выходные возвращать. Имя М-файла и
функции должно быть одним и тем же. Функции работают с переменными в пределах их собственного
рабочего пространства, отделенного от рабочего пространства, с которым вы оперируете в командной
строке MATLAB.
Основная программа
x = 2;
y = 3;
z = distance(x,y);
Page 9
Пример функции (сохранена в файле distance.m)
function c=distance(a,b)
c=sqrt(a^2+b^2);
10. Лекция 2. Вычисления в MATLAB. Числовые массивы:
2.1) техническое обеспечение САПР;2.2) вычисления в MATLAB;
2.3) числовые массивы, массивы символов.
Page 10
11. 2.3) Численные массивы
Задание одномерных массивовВектор-строку можно задать непосредственно в командной строке, используя оператор объединения [].
Например,
x=[1,2,3,4];
Второй способ задания вектора (с постоянным шагом)
x=1:0.001:5;
Замечание.
Точка с запятой в конце команды предотвращает вывод результатов вычислений в командное окно.
Например, если бы в команде x=1:0.001:5 не поставить в конце знак «;», то в рабочее поле были бы выведены
все 4001 значений массива.
Для обращения к элементу вектора, необходимо указать его индекс в круглых скобках, например
a = x(7);
% записывает в переменную а седьмой элемент массива x
x(8)=-1;
% присваивает восьмому элементу массива x значение -1
В MATLAB индексация начинается с единицы.
Задание двумерных массивов
Двумерный массив (матрицу) можно также, используя оператор объединения []. Например,
x=[1,2,3,4;5,6,7,8]
Для обращения к элементу матрицы, необходимо указать два индекса в круглых скобках через запятую,
например
x(1,2) = -1;
Кроме того, даже для многомерных массивов MATLAB поддерживает еще и одномерную индексацию,
сохраняя данные в постолбцовом порядке, эта традиция происходит от ФОРТРАНа.
Page 11
12. 2.3) Численные массивы
Индексация массивовПример 1
Выделить матрицу B из матрицы А
é 3 -2.5 4 1.3 0.7 ù
ê17 112 -1 2
3 ú
ú
A=ê
ê5
6
7 8
9 ú
ê
ú
7 û
ë10 11 10 9
→
é112 -1 2ù
B=ê
ú
ë 11 10 9 û
Решение
A = [3, -2.5, 4, 1.3, 0.7; 17, 112, -1, 2, 3;...
5, 6, 7, 8, 9; 10, 11, 10, 9, 7];
% ... означает продолжение кода на следующей строке
B = A([2,4], 2:4)
Пример 2
Написать программный код, который записывает все элементы матрицы А, которые меньше 0, в вектор В.
é 3 -2.5 4 1.3 0.7 ù
ê17 112 -1 2
3 ú
ê
ú
A=
ê5
6
7 8
9 ú
ê
ú
7 û
ë10 11 10 9
é -2.5ù
B=ê
ú
ë -1 û
Решение
Это проще всего сделать, используя индексацию с помощью логического массива
B=A(A<0)
Page 12
13. 2.3) Численные массивы
Функции для работы с массивамиКод
é 3 -2.5 4 1.3 0.7 ù
ê17 112 -1 2
3 ú
ú
A=ê
ê5
6
7 8
9 ú
ê
ú
7 û
ë10 11 10 9
Page 13
Результат
[m, n] = size(A)
m=4
n=5
N_len = length(A)
N_len = 5
N_len = length(A(:))
N_len = 20
N_num = numel(A)
N_num = 20
N_dim = ndims(A)
N_dim = 2
A = ones(2,3)
é1 1 1ù
A=ê
ú
ë1 1 1û
B = zeros(2,4)
é0 0 0 0ù
B=ê
ú
ë0 0 0 0û











 Программирование
Программирование Программное обеспечение
Программное обеспечение








