Дослідження синхронної системи управління з двома дискретними впливами та логічними умовами

1. Дослідження синхронної системи управління з двома дискретними впливами та логічними умовами

Виконав: студент гр. 1АВ-12б
Іванченко Д.М.
Науковий керівник: к.т.н., ст. викл. каф. КСУ Юхимчук
М.С.

2. Актуальність теми

▪ Потенціал використання синхронних систем управління дуже високий і в
багатьох сферах недооцінений економікою. При проектуванні та експлуатації
таких систем необхідно вміти моделювати та досліджувати чутливість
можливих відхилень параметрів синхронних систем управління на їх
показники якості роботи. Розв’язання таких задач дозволить проектувати
нечутливі або слабо чутливі до змінення їх первинних параметрів системи.
▪ Синхронні системи управління мають більш високий рівень надійності в
порівнянні з асинхронними системами управління. Такі системи здатні
функціонувати при появі відмов і жорсткому впливі навколишнього
середовища. Синхронні системи управління здатні забезпечити високу
робастність для систем нових зразків техніки.
2

3. Мета та предмет дослідження

▪ Метою роботи є забезпечення стійкого
функціонування синхронної системи управління
з двома дискретними впливами та логічними
умовами в умовах неконтрольованих змін їх
параметрів на основі нових та удосконалених
методів моделювання таких систем.
Мета та предмет
дослідження
▪ Предметом дослідження є математичні моделі
та методи моделювання синхронної системи
управління з двома дискретними впливами та
логічними умовами в умовах дії параметричних
збурень.
3

4. Використання методу фазових траєкторій

▪ Траєкторія руху точки M являє собою наочну
геометричну ілюстрацію динамічної поведінки
системи в процесі регулювання.
▪ Точка M називається зображуючою точкою, а її
траєкторія називається фазовою траєкторією, а
простір () називається фазовим простором.
▪ Фазовий простір і фазові траєкторії
представляють собою лише геометричний образ
динамічних процесів, які існують в системі. В цій
геометричній інтерпретації приймають лише
координати і виключено час. Фазова траєкторія
дає лише якісне представлення про характер
поведінки системи. Для визначення якісного
положення точки і, відповідно, стани системи в
деякий момент часу необхідно знайти розв'язок
диференціальних рівнянь в часі.
Використання
методу фазових
траєкторій
Рисунок 1 – Фазова траєкторія точки M
4

5.

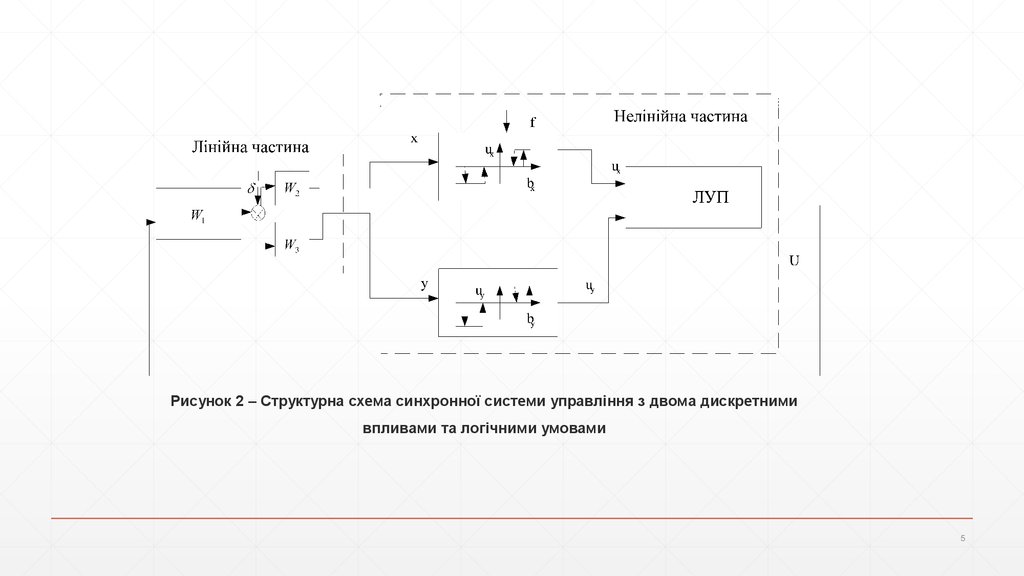
Рисунок 2 – Структурна схема синхронної системи управління з двома дискретними
впливами та логічними умовами
5

6.

Рисунок 3 – Результати моделювання синхронної системи
управління з двома дискретними впливами та логічними
умовами при: U1 = 2; U2 = 100; tx = 1.5; ty = 0.55
Рисунок 4 – Результати моделювання синхронної системи
управління з двома дискретними впливами та логічними
умовами при U1 = 2; U2 = 185.8; tx = 0.128; ty = 1.5
6

7.

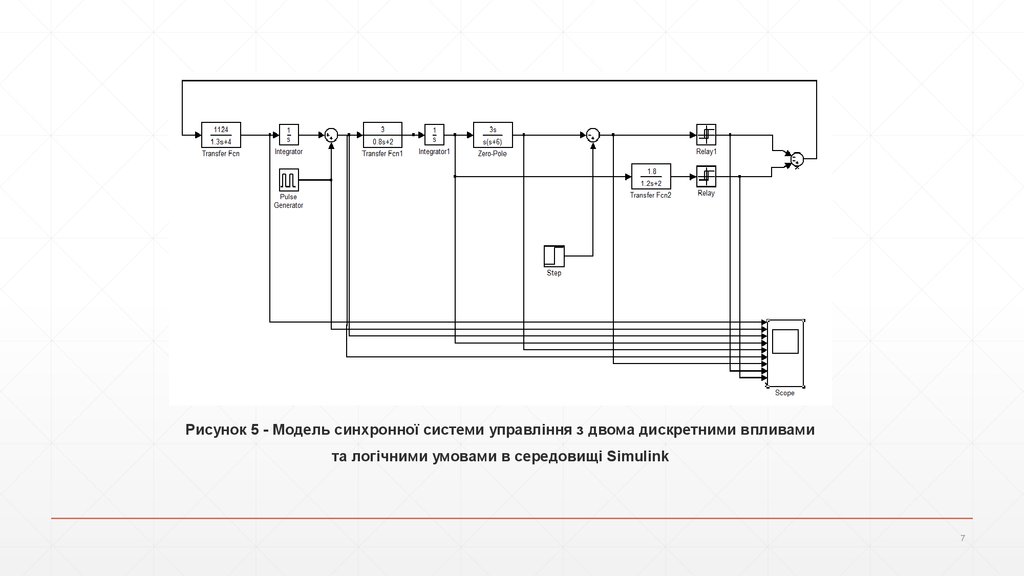
Рисунок 5 - Модель синхронної системи управління з двома дискретними впливами
та логічними умовами в середовищі Simulink
7

8. Рисунок 7 - Результати моделювання синхронної системи управління з двома дискретними впливами та логічними умовами при U1 = 2; U2 = 185.8; tx = 0.128; ty

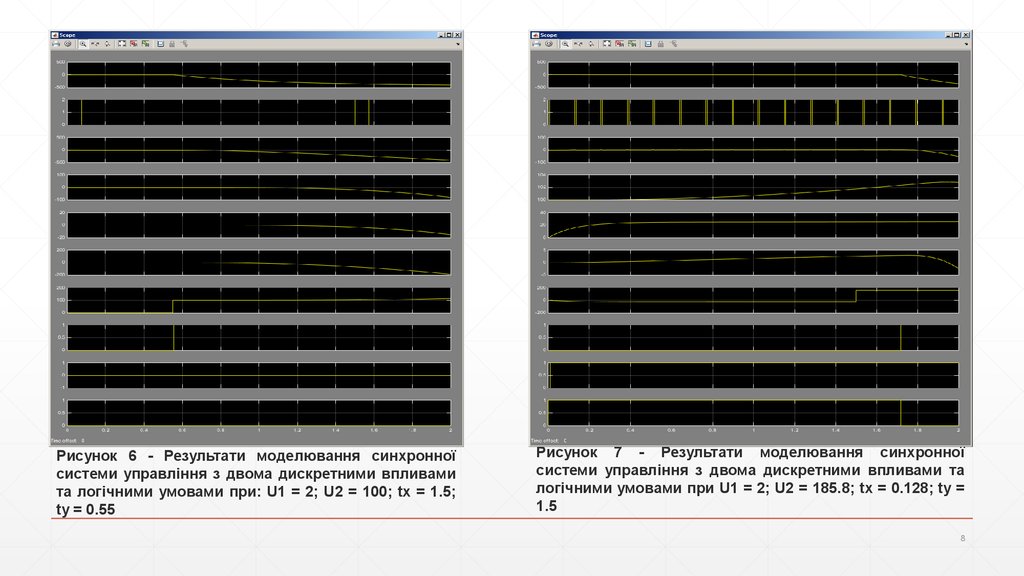
Рисунок 6 - Результати моделювання синхронної
системи управління з двома дискретними впливами
та логічними умовами при: U1 = 2; U2 = 100; tx = 1.5;
ty = 0.55
Рисунок 7 - Результати моделювання синхронної
системи управління з двома дискретними впливами та
логічними умовами при U1 = 2; U2 = 185.8; tx = 0.128; ty =
1.5
8

9. Висновки

▪ В бакалаврський дипломній роботі проведено аналіз існуючих методів
математичного моделювання, за допомогою яких розв’язують задачі
аналізу поведінки синхронних систем управління. Аналіз дозволив
зробити висновок, що існуючі результати не дозволяють
безпосередньо оцінити вплив зміни параметрів синхронних систем
управління на властивість стійкості та визначити області таких
параметрів, у яких зберігається їх стійкість, - тобто у межах існуючих
підходів неможливо розв’язати зворотні задачі робастної стійкості для
синхронних систем управління.
▪ Розроблено метод моделювання синхронних систем управління з
дискретними входами та логічними умовами, який дозволяє
враховувати вплив неконтрольованих параметричних збурень, що дає
можливість отримати аналітичну модель логічного пристрою меншої
складності, придатну для застосування в автоматизованих системах
проектування та діагностування відповідного класу систем.
Запропоновані математичні моделі для визначення параметрів
автоколивань систем управління з логічними умовами, які дозволяють
враховувати змінення первинних параметрів систем управління з
логічними управляючими пристроями при впливі на них
неконтрольованих параметричних збурень.
Висновки
▪ Проведений аналіз стійкості на прикладі синхронної системи
управління з двома дискретними входами та логічними умовами від
параметрів системи на основі підходу для дослідження нелінійних
систем з використанням методу фазових траєкторій.
9

10. Дякую за увагу!