Построение треугольника

1.

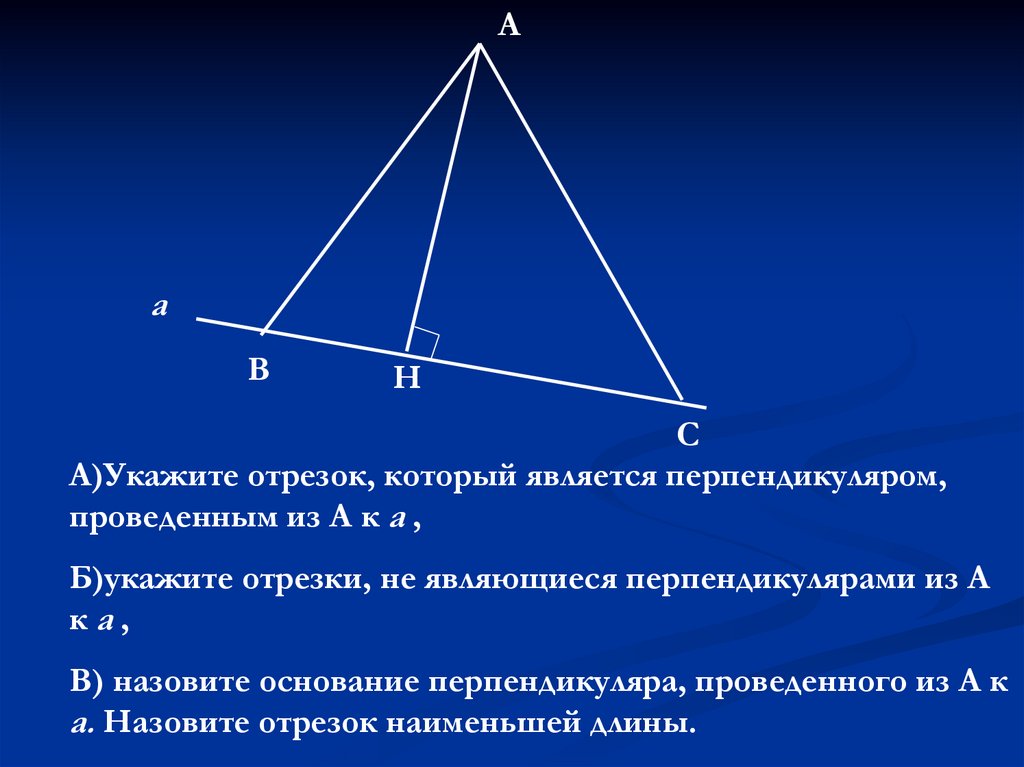
А
а
В
Н
С
А)Укажите отрезок, который является перпендикуляром,
проведенным из А к а ,
Б)укажите отрезки, не являющиеся перпендикулярами из А
ка,
В) назовите основание перпендикуляра, проведенного из А к
а. Назовите отрезок наименьшей длины.

2.

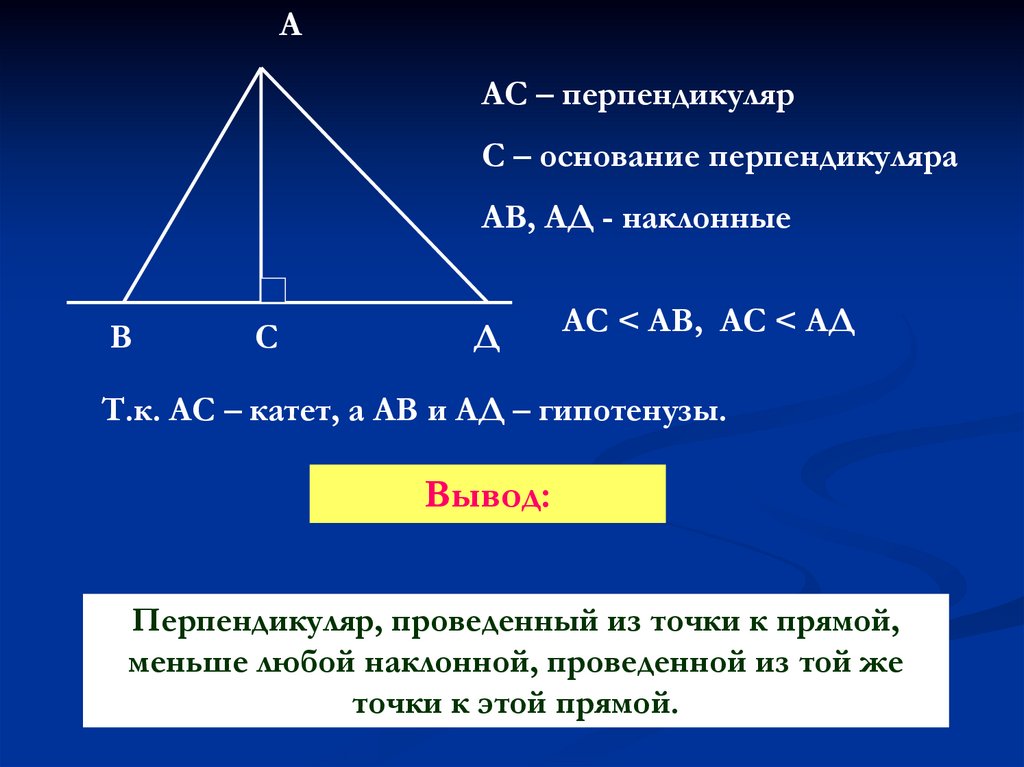
А
АС – перпендикуляр
С – основание перпендикуляра
АВ, АД - наклонные
В
С
Д
АС < АВ, АС < АД
Т.к. АС – катет, а АВ и АД – гипотенузы.
Вывод:
Перпендикуляр, проведенный из точки к прямой,
меньше любой наклонной, проведенной из той же
точки к этой прямой.

3.

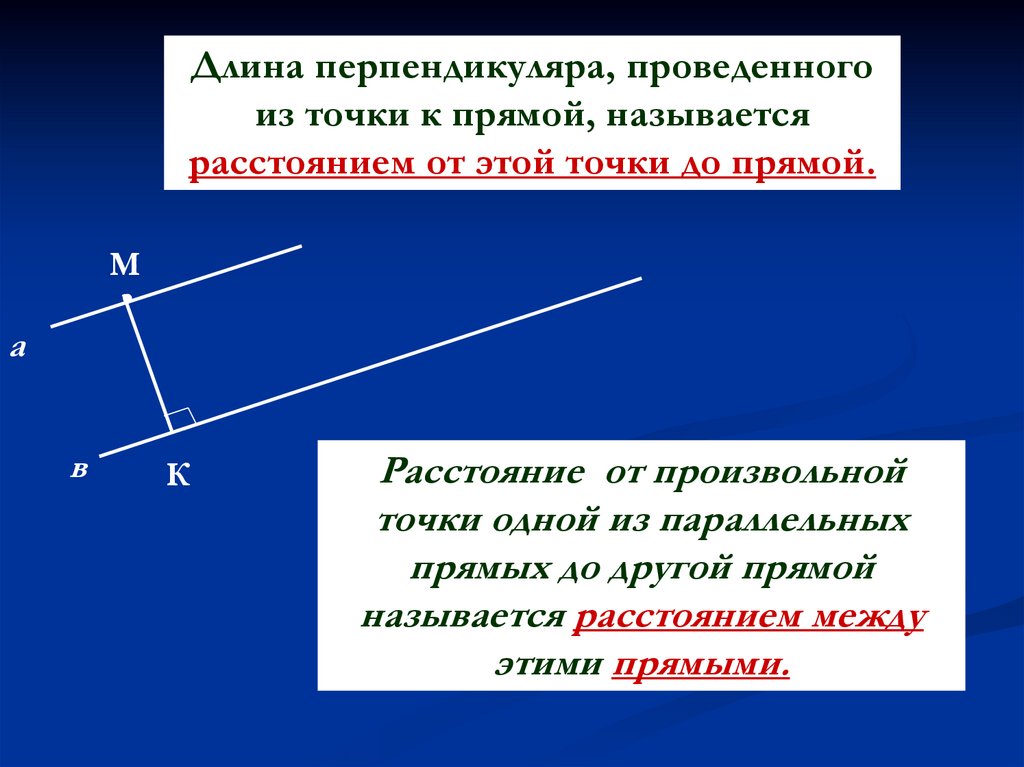
Длина перпендикуляра, проведенного
из точки к прямой, называется
расстоянием от этой точки до прямой.
М
а
в
К
Расстояние от произвольной
точки одной из параллельных
прямых до другой прямой
называется расстоянием между
этими прямыми.

4.

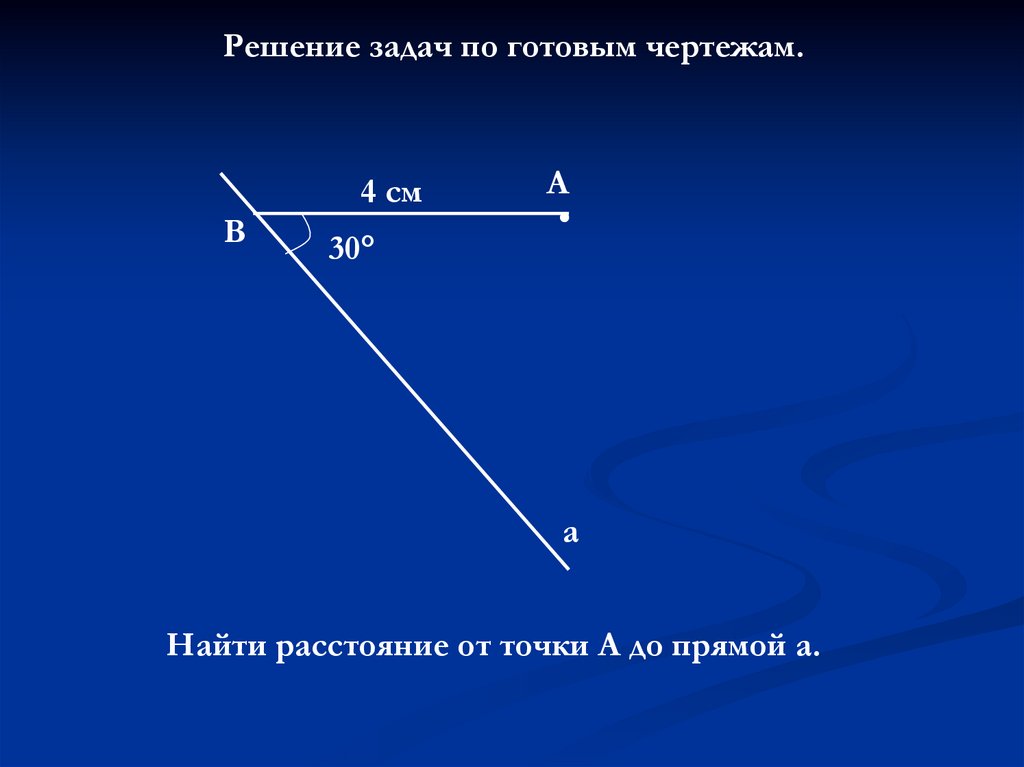
Решение задач по готовым чертежам.
4 см
В
А
30°
а
Найти расстояние от точки А до прямой а.

5.

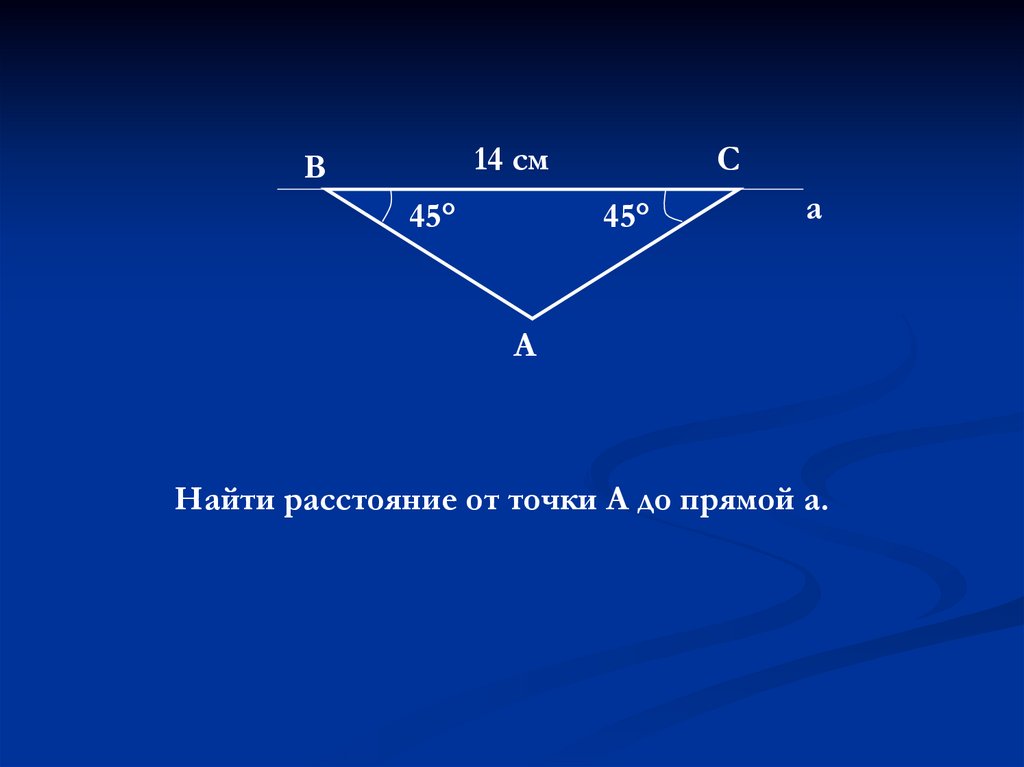
14 см
В
45°
С
45°
а
А
Найти расстояние от точки А до прямой а.

6.

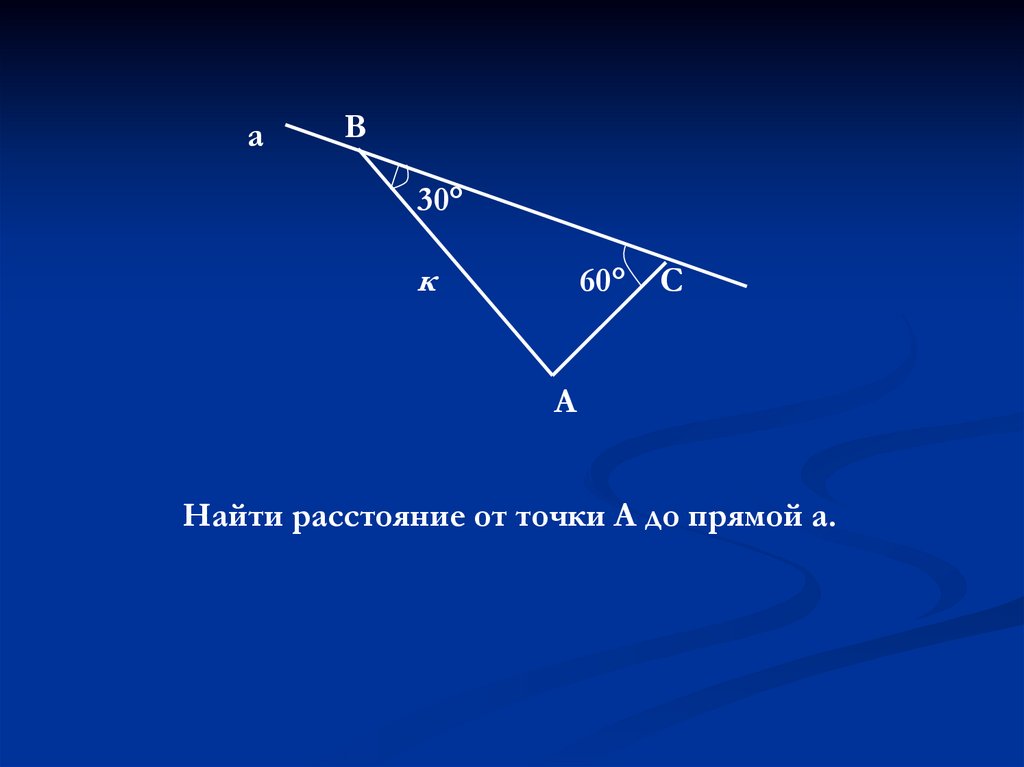
а
В
30°
к
60°
С
А
Найти расстояние от точки А до прямой а.

7.

а
К
< 1 = < 2.
КА = 7 см.
1 2
А
30°
N
60°
М
Найти расстояние от точки А до прямой а.

8.

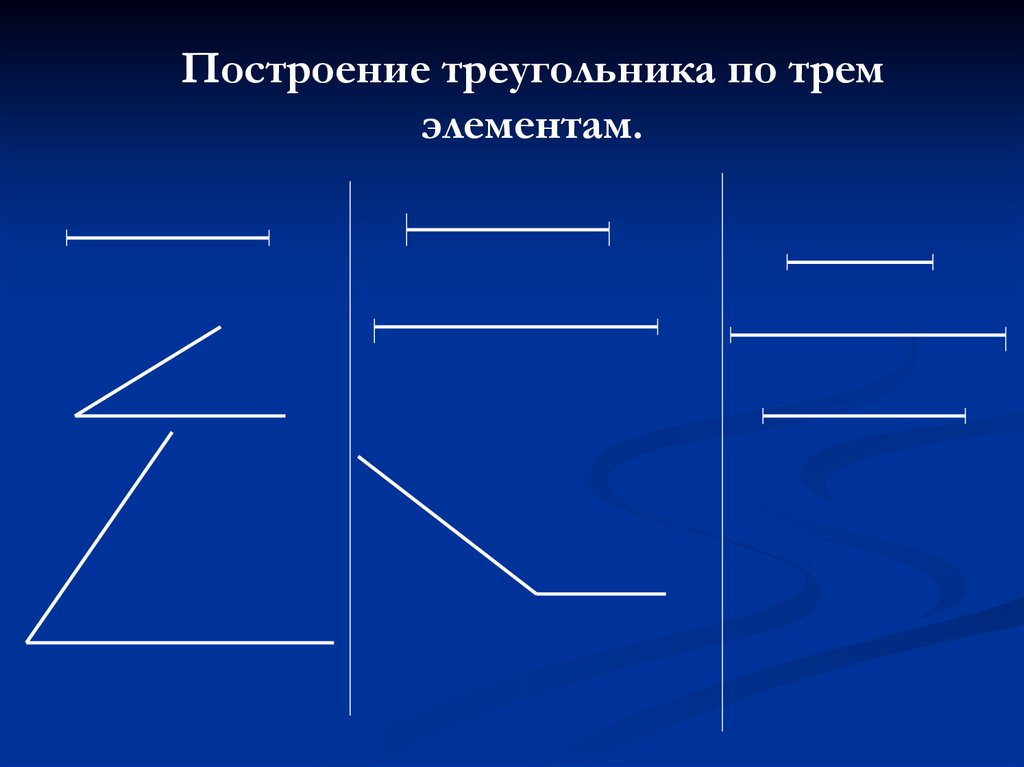
Построение треугольника по трем
элементам.

9.

Устное решение задач по готовым чертежам
1)
2)
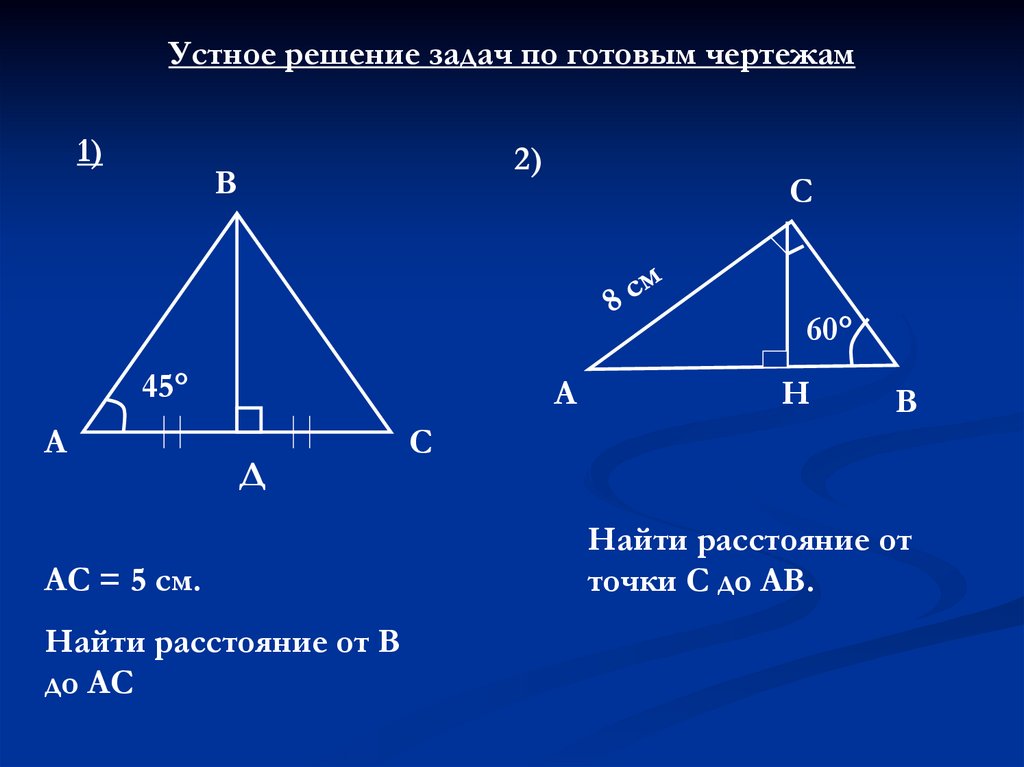
В
С
60°
45°
А
А
Д
АС = 5 см.
Найти расстояние от В
до АС
Н
В
С
Найти расстояние от
точки С до АВ.

10.

1. С помощью циркуля , линейки и транспортира
постройте ΔАВС, в котором АВ = 4 см, ВС = 5 см,
<В = 70°.
2. С помощью циркуля, линейки и транспортира
постройте ΔАВС, в котором АВ = 6 см, < А = 50°,
<В = 80°.
3. С помощью циркуля и линейки с делениями
постройте ΔАВС такой, что АВ = 5 см, ВС = 6 см,
АС = 7 см.

11.

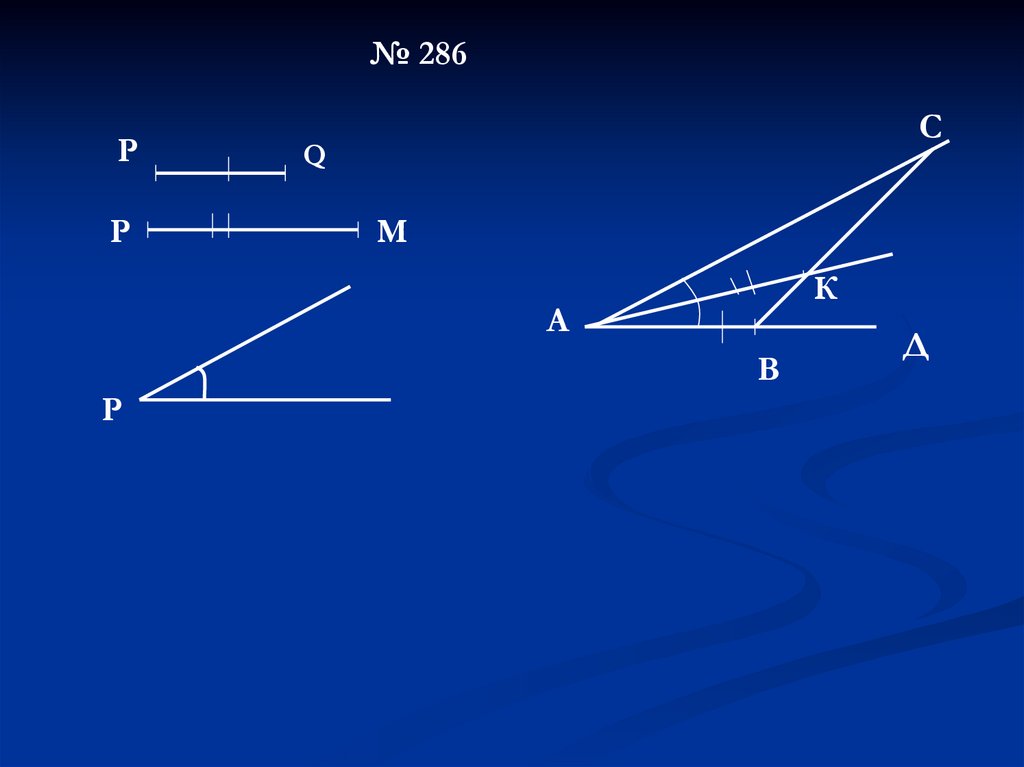
№ 286
Р
Р
С
Q
М
К
А
В
Р
Д

12.

№ 291(д)
Р
Q
S
Т
Дано: медиана РQ, проведенная
к основанию; основание
равнобедренного треугольника
ST.
Построение:
1)Строим АВ , равный ST.
2)Строим М – середину АВ.
3) Через М проводим в ┴ АВ и на ней от М отложим
МС = РQ.
4) Соединим А и С, В и С. (2 решения)

13.

Д/з. № 281, 285, 287

14.

№ 285
а
Х
А
У
Р
в
к
с
Q

15.

14 см
В
45°
С
45°
а
А
Найти расстояние от точки А до прямой а.

16.

Построение треугольника по трем
элементам.