Признаки параллельности прямых. Задачи

1.

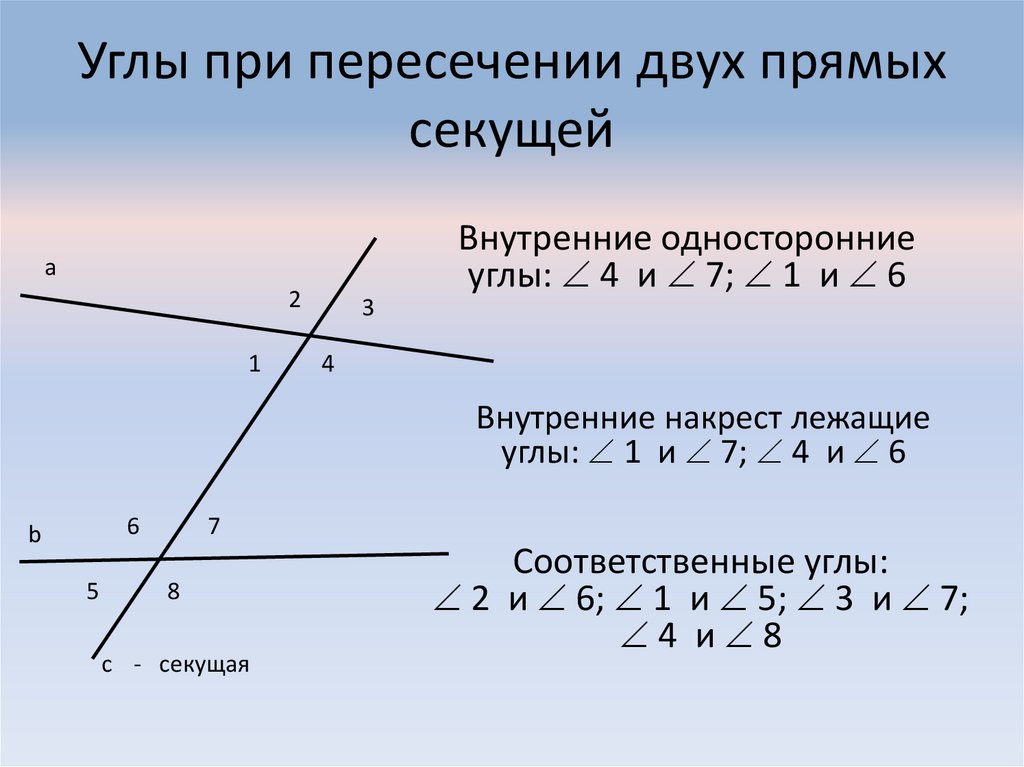
2. Углы при пересечении двух прямых секущей

а
2
1
3
Внутренние односторонние
углы: 4 и 7; 1 и 6
4
Внутренние накрест лежащие
углы: 1 и 7; 4 и 6
6
b
5
7
8
с - секущая
Соответственные углы:
2 и 6; 1 и 5; 3 и 7;
4 и 8

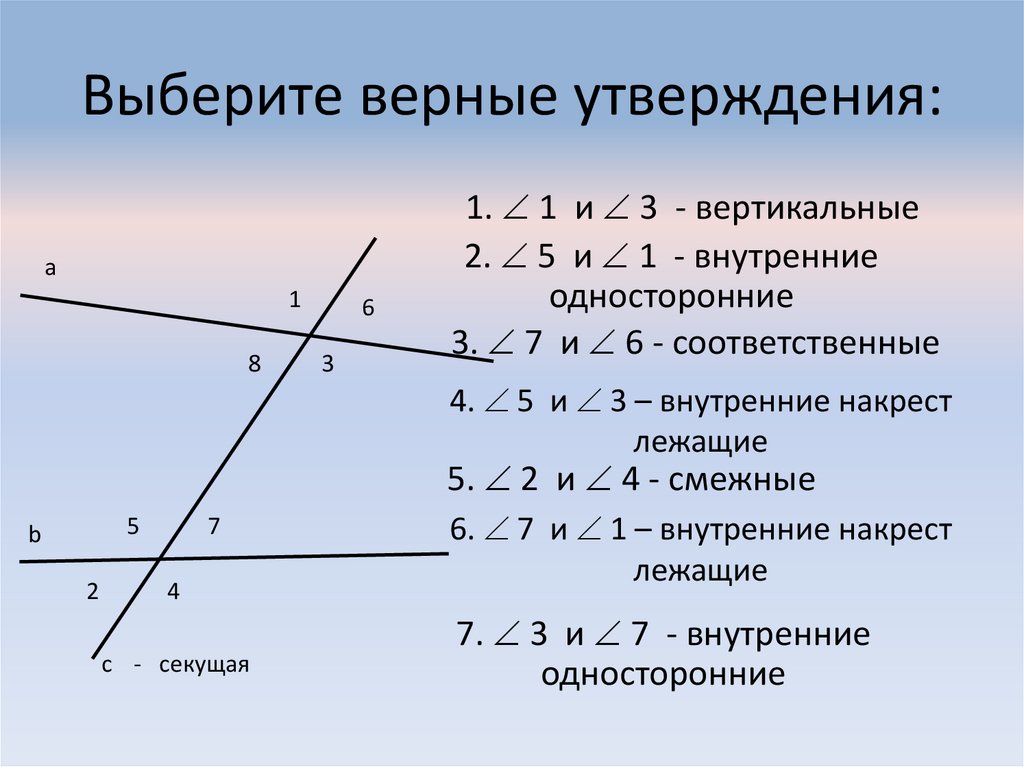
3. Выберите верные утверждения:

а
1
8
6
3
1. 1 и 3 - вертикальные
2. 5 и 1 - внутренние
односторонние
3. 7 и 6 - соответственные
4. 5 и 3 – внутренние накрест
лежащие
5. 2 и 4 - смежные
5
b
2
7
4
с - секущая
6. 7 и 1 – внутренние накрест
лежащие
7. 3 и 7 - внутренние
односторонние

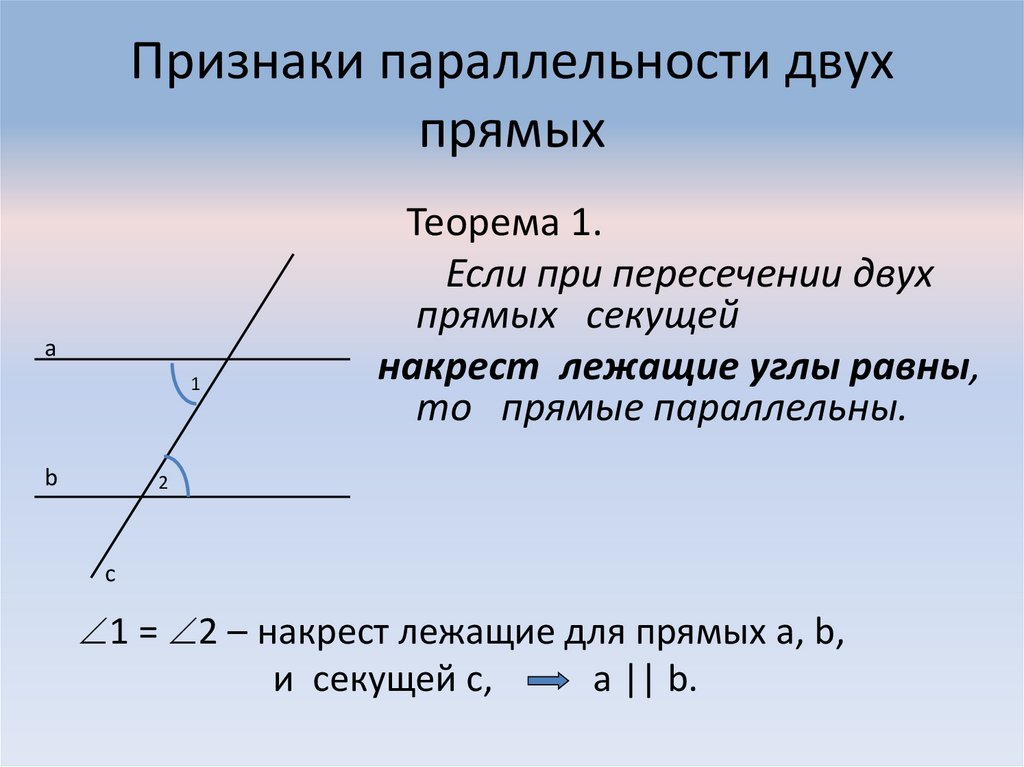
4. Признаки параллельности двух прямых

а
1
b
Теорема 1.
Если при пересечении двух
прямых секущей
накрест лежащие углы равны,
то прямые параллельны.
2
c
1 = 2 – накрест лежащие для прямых а, b,
и секущей с,
а || b.

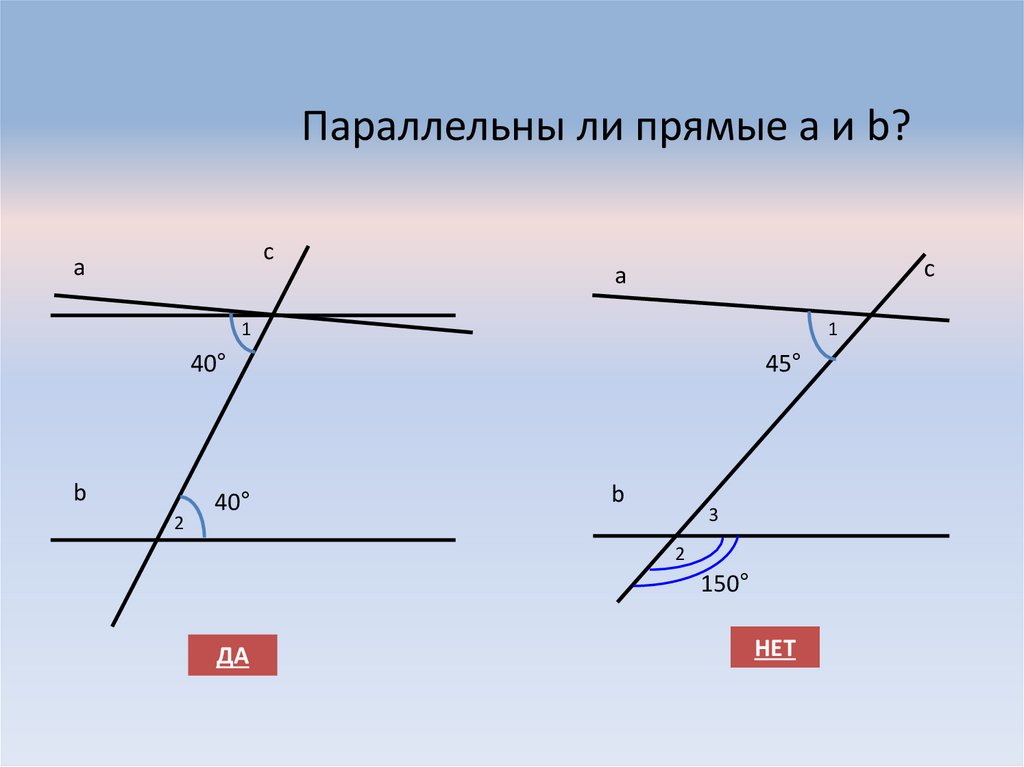
5. Параллельны ли прямые а и b?

с
а
с
а
1
1
40°
b
2
40°
45°
b
3
2
150°
ДА
НЕТ

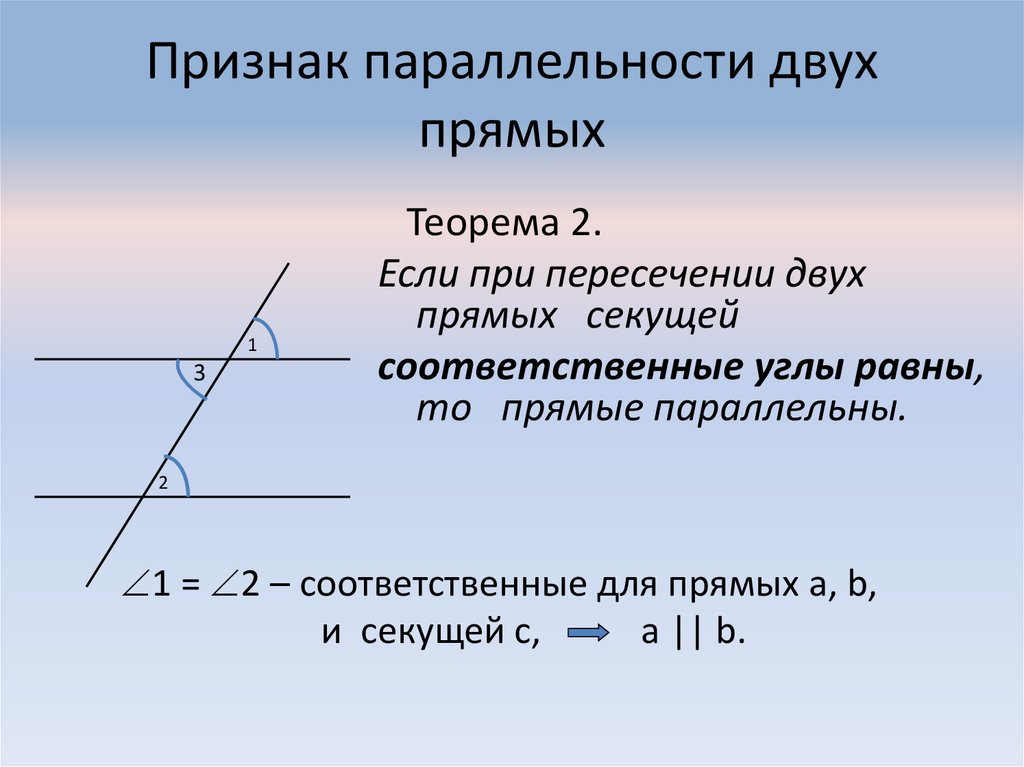
6. Признак параллельности двух прямых

1
3
Теорема 2.
Если при пересечении двух
прямых секущей
соответственные углы равны,
то прямые параллельны.
2
1 = 2 – соответственные для прямых а, b,
и секущей с,
а || b.

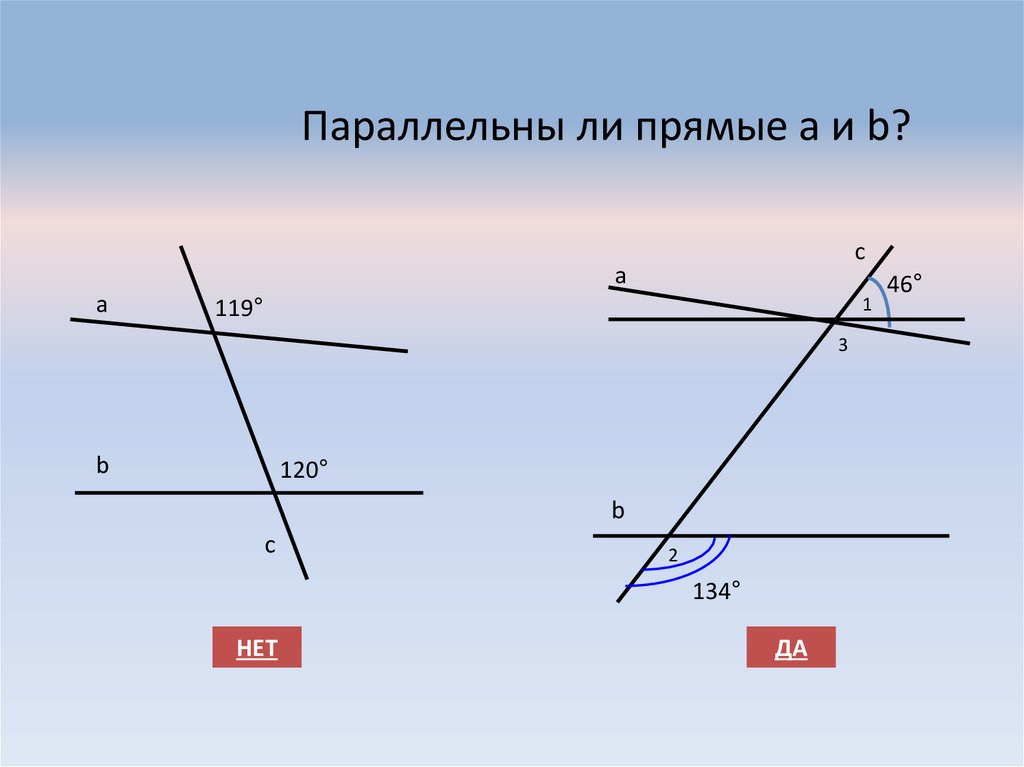
7. Параллельны ли прямые а и b?

с
а
а
1
119°
3
b
120°
b
с
2
134°
НЕТ
ДА
46°

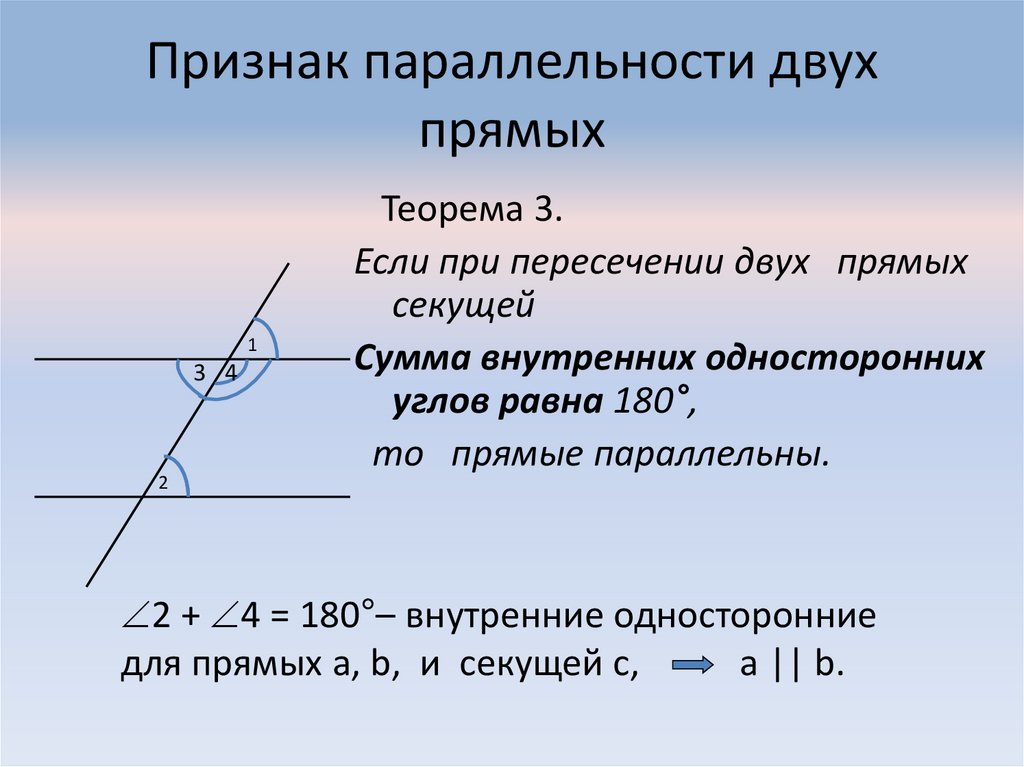
8. Признак параллельности двух прямых

1
3 4
2
Теорема 3.
Если при пересечении двух прямых
секущей
Сумма внутренних односторонних
углов равна 180°,
то прямые параллельны.
2 + 4 = 180°– внутренние односторонние
для прямых а, b, и секущей с,
а || b.

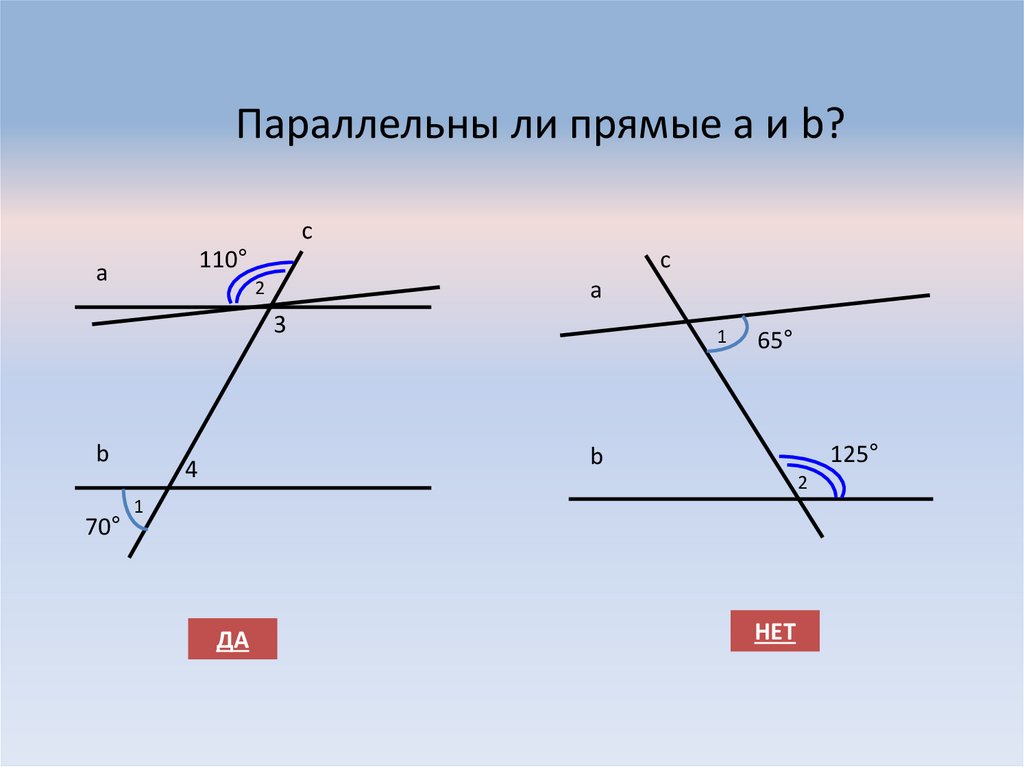
9. Параллельны ли прямые а и b?

с
с
110°
а
а
2
3
b
70°
1
65°
125°
b
4
2
1
ДА
НЕТ

10. Учебник № 188

Отрезки АВ и СD пересекаются в их общей середине. Докажите, что
прямые АС и ВD параллельны.
D
Д а н о: АВ ∩ СD = К, АК = КВ, СК = КD.
В
4
Д о к а з а т ь: АС || ВD.
2
1
Д о к а з а т е л ь с т в о:
К
3
А
С
Выберите секущую для прямых АС , ВD .
Найдите накрест лежащие углы
и докажите их равенство.
Доказательство:
1. Рассмотрим
АКС и
ВКD:
АКС = ВКD
По двум сторонам и
АК=КВ, СК=КD – по условию,
углу между ними
1 = 2 – по свойству вертикальных углов
2. 3 = 4 – соответственные элементы равных треугольников в п.1.
3. 3 = 4 – это накрест лежащие углы при прямых АС , ВD
и секущей СD, значит АС || ВD по признаку параллельности прямых Ч.Т.Д.

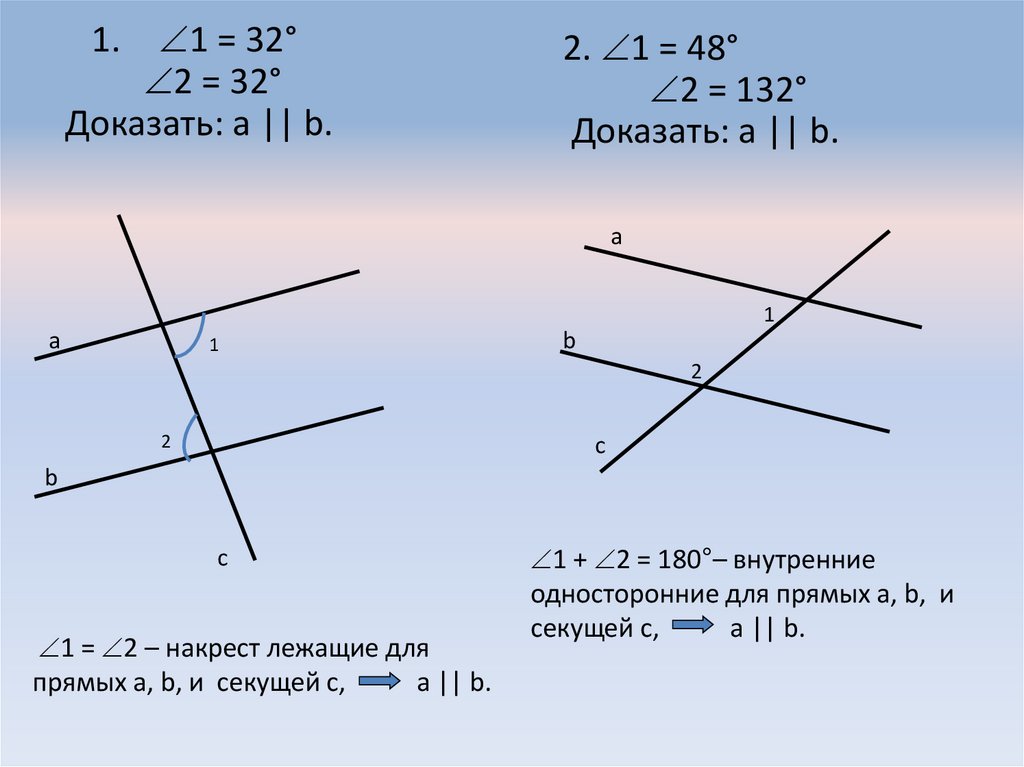
11.

1 = 32°
2 = 32°
Доказать: а || b.
1.
2. 1 = 48°
2 = 132°
Доказать: а || b.
а
1
а
1
b
2
2
c
b
c
1 = 2 – накрест лежащие для
прямых а, b, и секущей с,
а || b.
1 + 2 = 180°– внутренние
односторонние для прямых а, b, и
секущей с,
а || b.

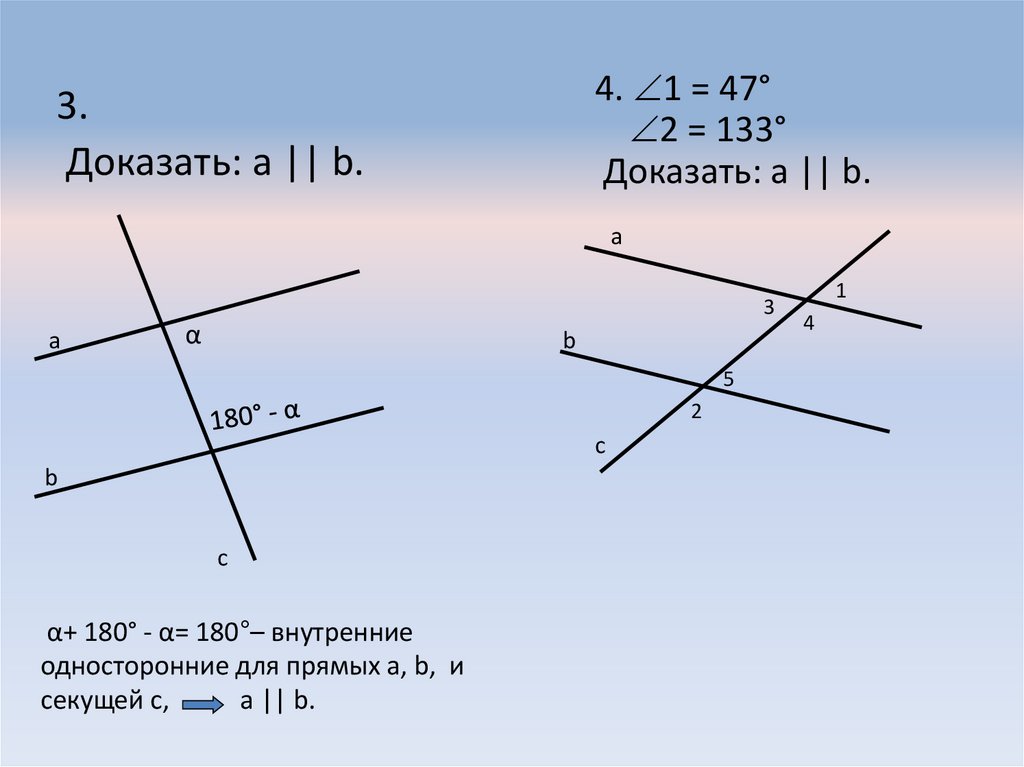
12.

4. 1 = 47°
2 = 133°
Доказать: а || b.
3.
Доказать: а || b.
а
3
а
α
b
5
2
c
b
c
α+ 180° - α= 180°– внутренние
односторонние для прямых а, b, и
секущей с,
а || b.
1
4

13.

5. 1 = 2 = 3
Доказать: а || b,
6. 1 = 83°
2 больше 1 на 14°
Доказать: AB || MN.
с || d.
B
а
3
2
1
2
N
1
A
b
d
c
1 = 2 – соответственные для
прямых а, b, и секущей с,
а || b.
3 = 2 – накрест лежащие для
прямых с, d, и секущей a,
c || d.
M
C

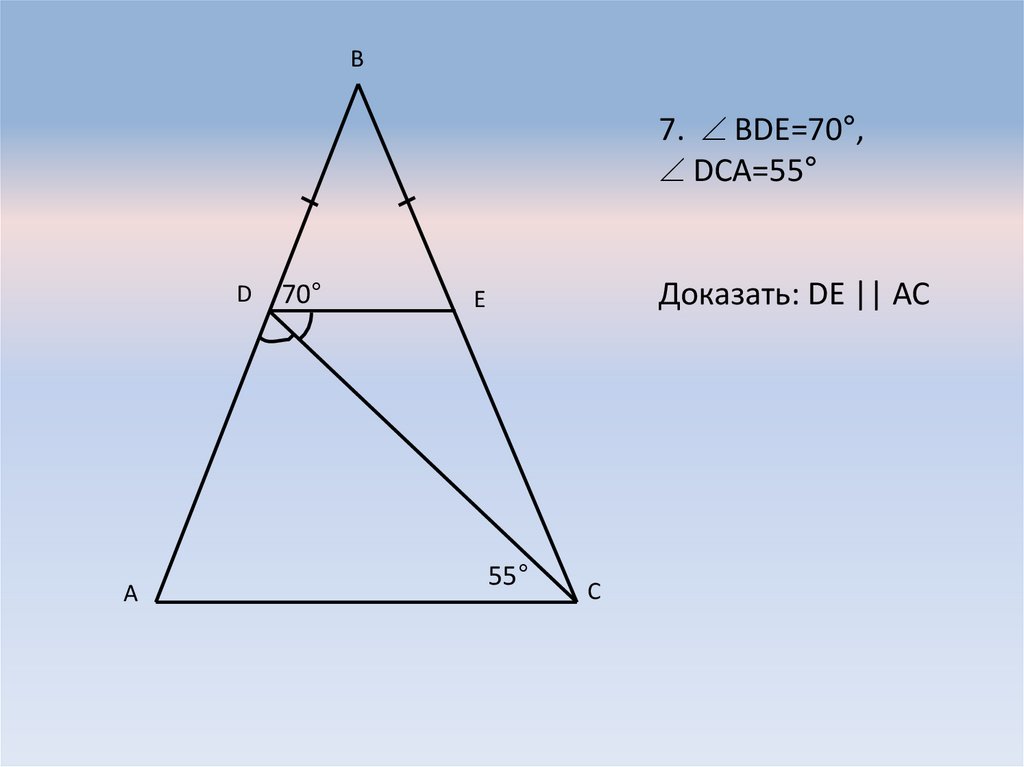
14.

В
7. BDE=70°,
DCA=55°
D
А
70°
Доказать: DE || AC
E
55°
С

15.

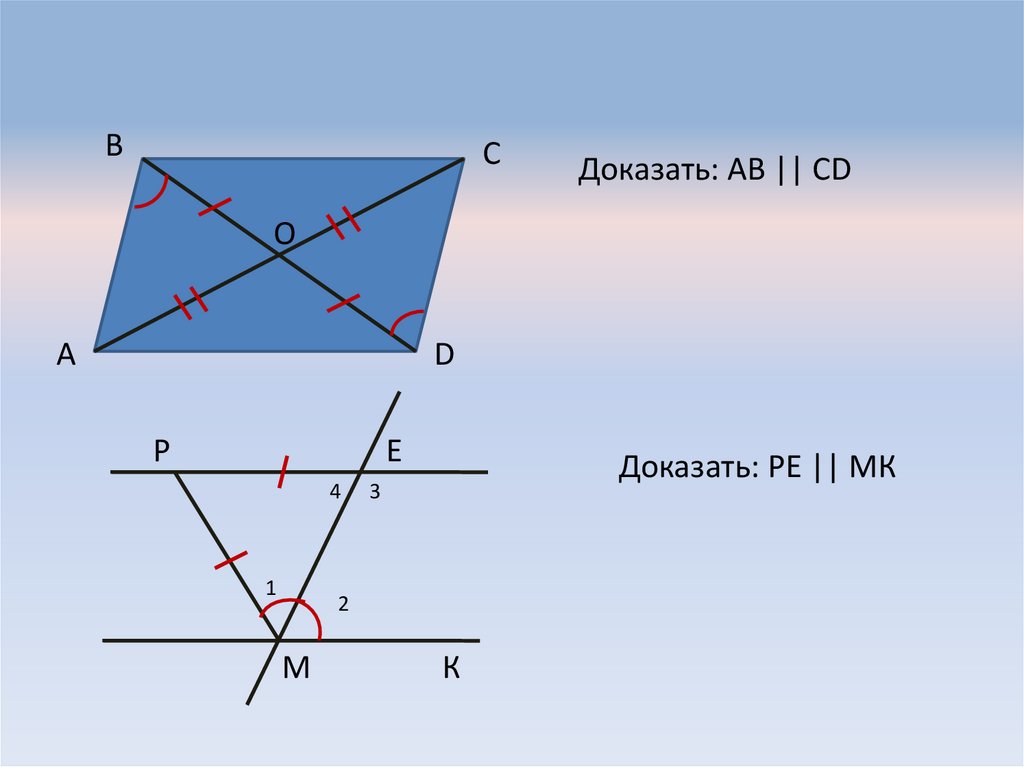
В
С
Доказать: AB || CD
О
А
D
Р
Е
4
1
Доказать: РЕ || МК
3
2
М
К

16.

Список литературы:
1. Геометрия 7-9. Учебник для общеобразовательных
учреждений. Л.С. Атанасян и др. М. «Просвещение», 2010г.
2. «Алгебра. Геометрия.» Самостоятельные и контрольные
работы для 7 класса. А.П. Ершова.М. «ИЛЕКСА», 2009г.