Теорема о пересечении высот треугольника

1. Замечательные точки треугольника Урок 3. Теорема о пересечении высот треугольника.

Презентация выполнена учителем
математики МБОУ СОШ № 22
Лисицыной Татьяной Петровной,
п. Пересыпь,
Темрюкский район, Краснодарский край

2. Цели:

1) Рассмотреть теорему о точке пересечения
высот и следствие из неё;
2) Формировать умения применять известные
знания в незнакомой ситуации, сравнивать,
анализировать, обобщать.
3) Воспитывать ответственное отношение к
обучению, умение оценивать свой труд, а
также аккуратность, точность и
внимательность при работе с чертёжными
инструментами.

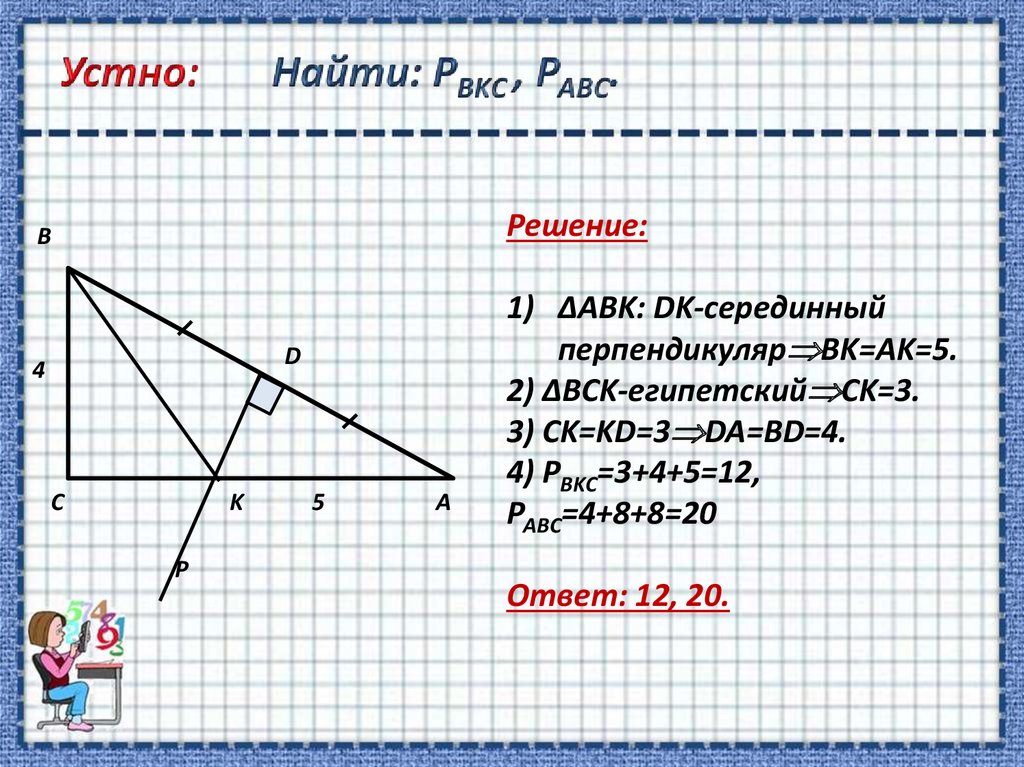
3. Устно: Найти: РВKС , РАВС.

Решение:
B
D
4
С
K
P
5
А
1) ΔABK: DK-серединный
перпендикуляр BK=AK=5.
2) ΔBCK-египетский CK=3.
3) CK=KD=3 DA=BD=4.
4) РВKС=3+4+5=12,
РАВС=4+8+8=20
Ответ: 12, 20.

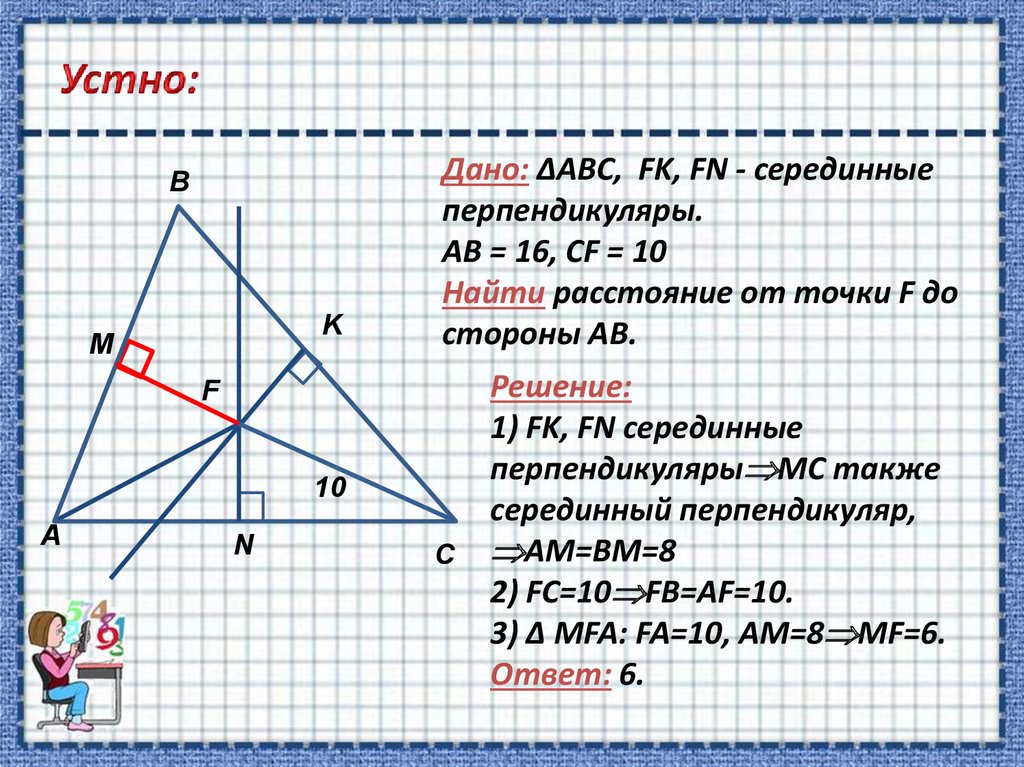
4. Устно:

B
K
M
Дано: ΔABC, FK, FN - серединные
перпендикуляры.
АВ = 16, СF = 10
Найти расстояние от точки F до
стороны АВ.
F
10
А
N
C
Решение:
1) FK, FN серединные
перпендикуляры MC также
серединный перпендикуляр,
AM=BM=8
2) FC=10 FB=AF=10.
3) Δ MFA: FA=10, АM=8 MF=6.
Ответ: 6.

5.

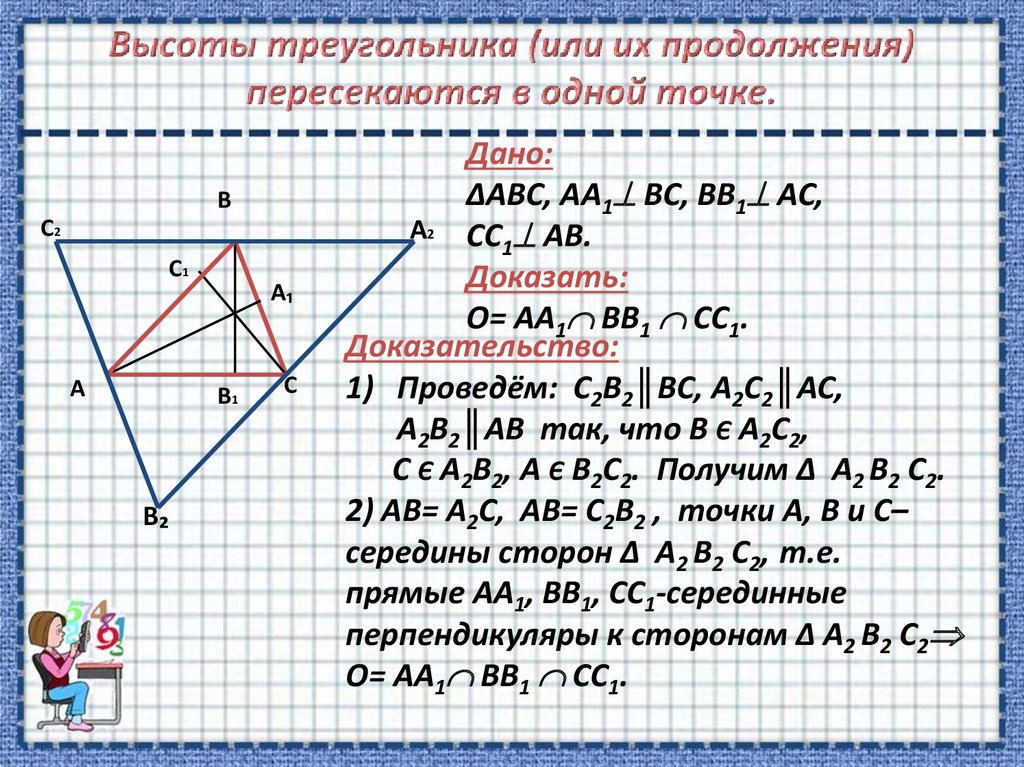
6. Высоты треугольника (или их продолжения) пересекаются в одной точке.

В
С2
С1
А
А₁
В1
В₂
С
Дано:
ΔABC, AA1 BC, BB1 AC,
А2 CC AB.
1
Доказать:
O= AA1 BB1 CC1.
Доказательство:
1) Проведём: С2B2║BC, A2C2║AC,
A2B2║AB так, что B Є A2C2,
C Є A2B2, A Є B2C2. Получим Δ A2 B2 C2.
2) AB= A2C, AB= С2B2 , точки A, B и C–
середины сторон Δ A2 B2 C2, т.е.
прямые АА1, BB1, CC1-серединные
перпендикуляры к сторонам Δ A2 B2 C2
O= AA1 BB1 CC1.

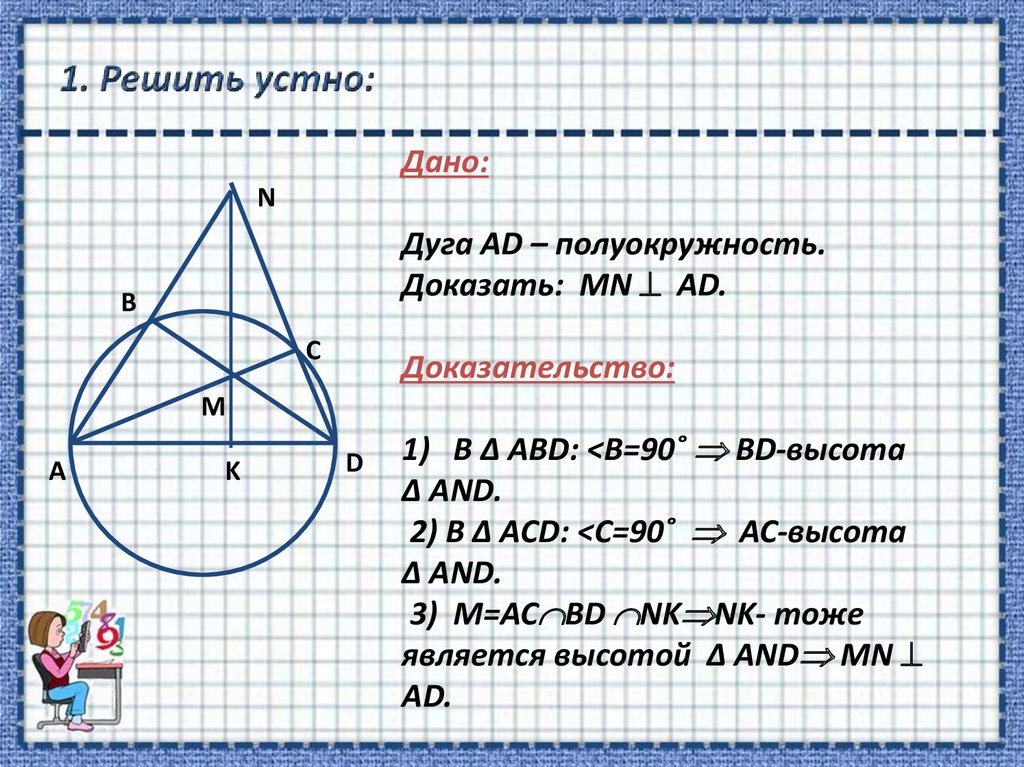
7. 1. Решить устно:

Дано:
N
Дуга АD – полуокружность.
Доказать: MN АD.
B
C
Доказательство:
M
А
K
D
1) В Δ ABD: <B=90˚ BD-высота
Δ AND.
2) В Δ AСD: <С=90˚ АС-высота
Δ AND.
3) M=AC BD NK NK- тоже
является высотой Δ AND MN
АD.

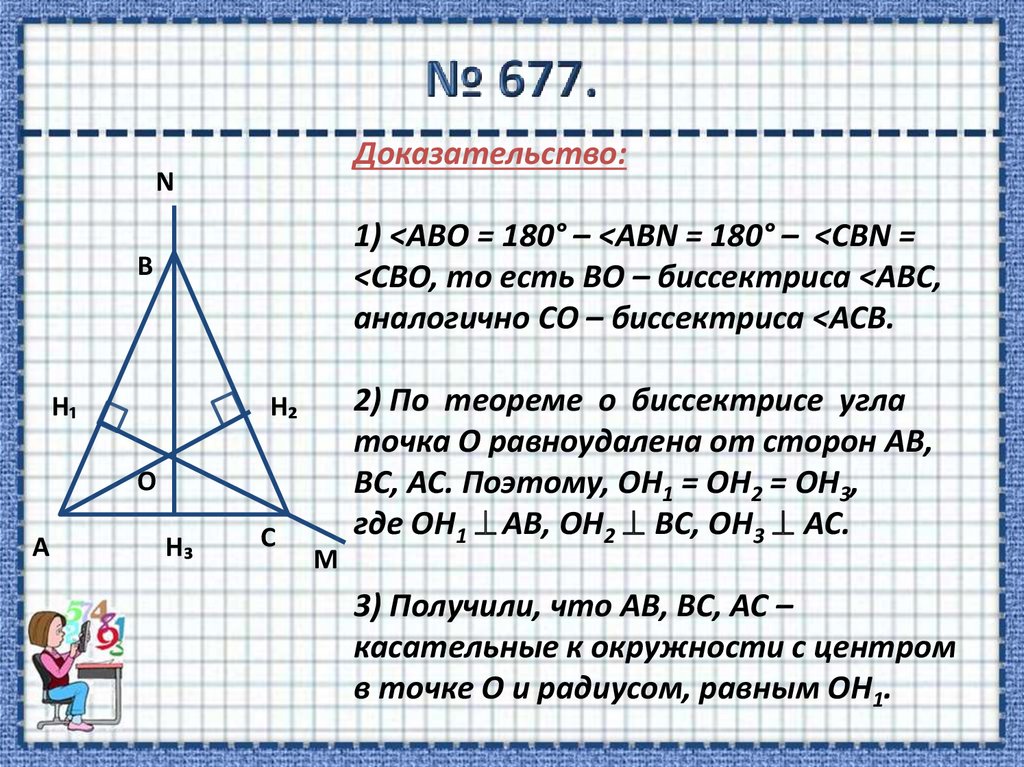
8. № 677.

Доказательство:
N
1) <АВО = 180° – <АВN = 180° – <СВN =
<CВО, то есть ВО – биссектриса <АВС,
аналогично СО – биссектриса <АСВ.
B
H₁
H₂
O
А
H₃
C
M
2) По теореме о биссектрисе угла
точка О равноудалена от сторон АВ,
ВС, АС. Поэтому, ОН1 = ОН2 = ОН3,
где ОН1 АВ, ОН2 ВС, ОН3 АС.
3) Получили, что АВ, ВС, АС –
касательные к окружности с центром
в точке О и радиусом, равным ОН1.

9. № 684

C
M
А
Доказательство:
1) По свойству углов при основании
равнобедренного треугольника
<САВ = <СВА. Тогда <МАС = <МАВ =
<САВ = <СВА = <МВС = <МВА.
2) Δ МАВ – равнобедренный, АМ = ВМ
и точка М лежит на серединном
перпендикуляре к АВ.
B 3) Так как АС = СВ, то точка С также
лежит на серединном
перпендикуляре к АВ.
Поэтому СМ АВ.

10.

11.

Домашнее задание:
вопросы 1– 20, с. 187–188; №№ 688, 720.

12.

Использованная литература
1. Атанасян Л.С. и др. Геометрия 7-9 классы. –
М:, Просвещение, 2008г.
2. Атанасян Л.С., Бутузов В.Ф. и др. «Изучение
геометрии в 7-9 классе». Методические рекомендации.
М:, Просвещение, 2007г.
3. Зив Б.Г., Мейлер В.М. «Дидактические материалы по
геометрии. 8 кл». М:, Просвещение, 2007г.

13. Для создания шаблона использовались источники:

http://www.myjulia.ru/data/cache/2009/07/17/152778_22660x600.jpg
http://files.botevcheta.webnode.com/20000001645175461c2/1stationery15-med.jpg
http://www.mathknowledge.com/images/custom/LOGO.GIF
http://www.ccboe.net/Teachers/Durham_Sharon/images/918F94220
10B4BB0B160956D6B9D4E34.JPG
http://lake.k12.fl.us/cms/cwp/view.asp?A=3&Q=427619
http://www.533school.ru/nach.htm
Автор данного шаблона: Ермолаева Ирина Алексеевна учитель
информатики и математики МОУ «Павловская сош» с.Павловск
Алтайский край