Похожие презентации:
Решение уравнений из материалов ЕГЭ по математике
1.
«Решение уравненийиз материалов ЕГЭ
по математике»
2.
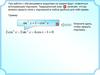
а). Решите уравнениеsin 2 x
б). Найдите все корни этого уравнения,
2 sin x cos x
принадлежащие отрезку
2 cos x 1 sin 2 х sin х
3
;
2
2 cos х 1 2 sin x cos x sin x
2 cos х 1 sin x 2 cos x 1
1 2 cos х 1 sin x 2 cos x 1 0
1
2
1
1 sin x 2arccos
cos x 1 0 arccos
2
3
3
2
1
sin x 1
cos x
2
1
х arccos 2 n
x 2 n
2
2
2
х
2 n;
3
3.
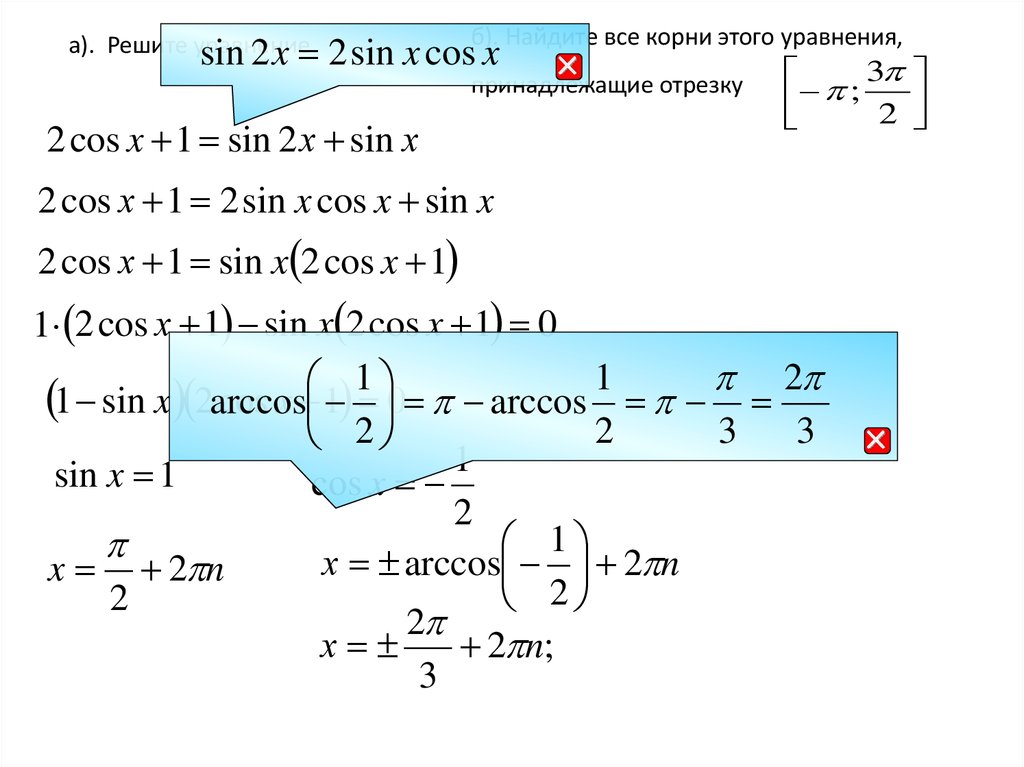
Отбор корней с помощью графиковб). Найдите все корни этого уравнения, принадлежащие отрезку
2
2
3
2
y sin x
y
sin x 1
1
2
-1
3
;
2
2
2 4
x
3
2
2
б ). ;
;
;
.
2 3 3
3
2
4.
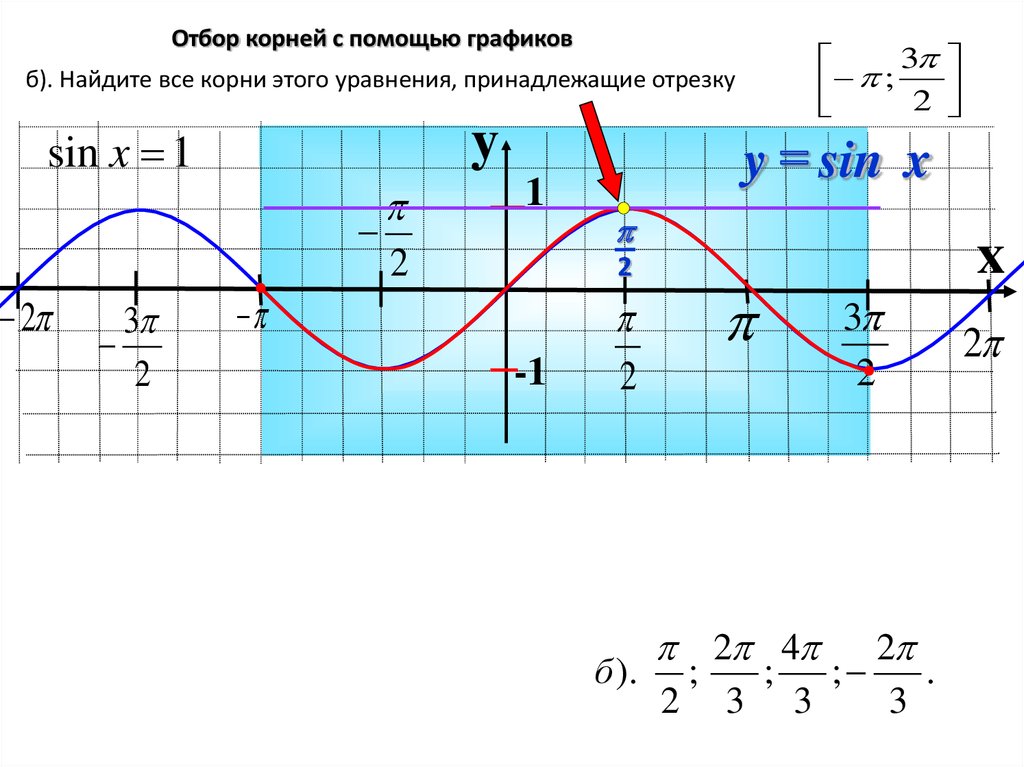
Отбор корней с помощью графиковб). Найдите все корни этого уравнения, принадлежащие отрезку
1
cos x
2
3
- 8
3
5
2
y cos x
2
- 4
3
3
2
2
4
3
9
8
.
3
2 6
6 6
6
y
1
x
5 3
15
16
8
.
2 6
6
6
6
3
3
3 ;
-1
5.
3sin
x
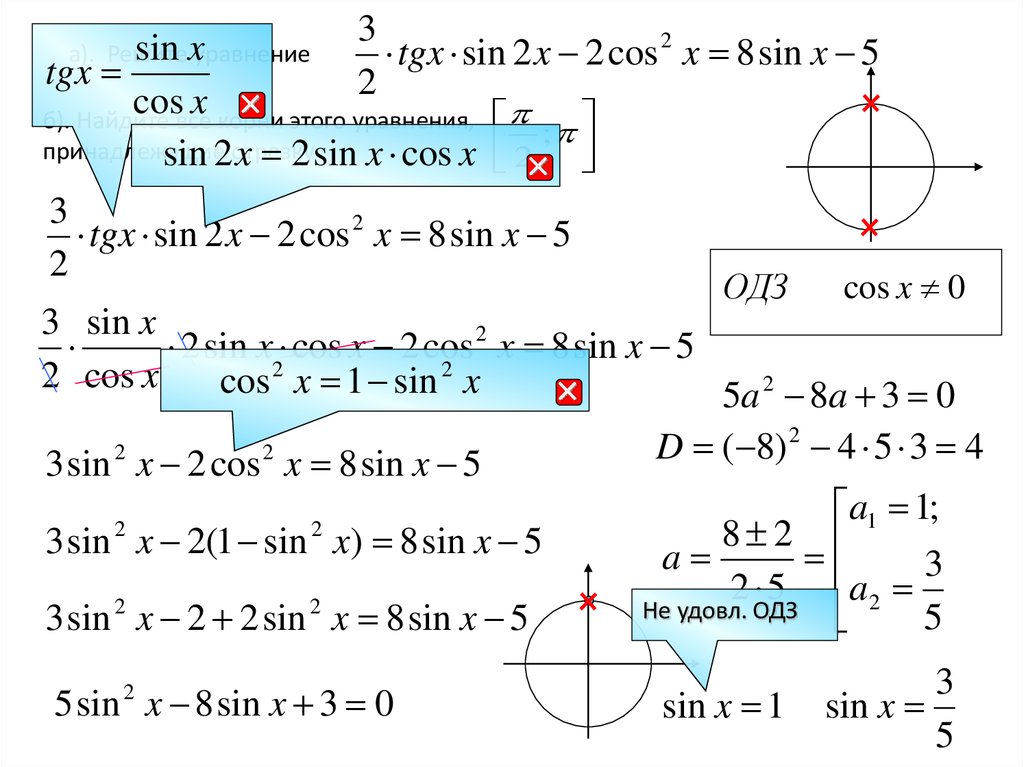
а). Решите уравнение
tgx sin 2 x 2 cos 2 x 8 sin x 5
tgx
2
cos x
б). Найдите все корни этого уравнения,
;
принадлежащие
sin 2отрезку
x 2 sin x cos x 2
3
tgx sin 2 x 2 cos 2 x 8 sin x 5
2
ОДЗ
cos x 0
3 sin x
2
2 sin x2 cos x 2 cos
x
8
sin
x
5
2 cos x
cos x 1 sin 2 x
3 sin 2 x 2 cos 2 x 8 sin x 5
3 sin x 2(1 sin x) 8 sin x 5
2
2
3 sin 2 x 2 2 sin 2 x 8 sin x 5
5 sin x 8 sin x 3 0
2
5a 2 8a 3 0
D ( 8) 2 4 5 3 4
a1 1;
8 2
a
3
2 5
a2
Не удовл. ОДЗ
5
sin x 1
3
sin x
5
6.
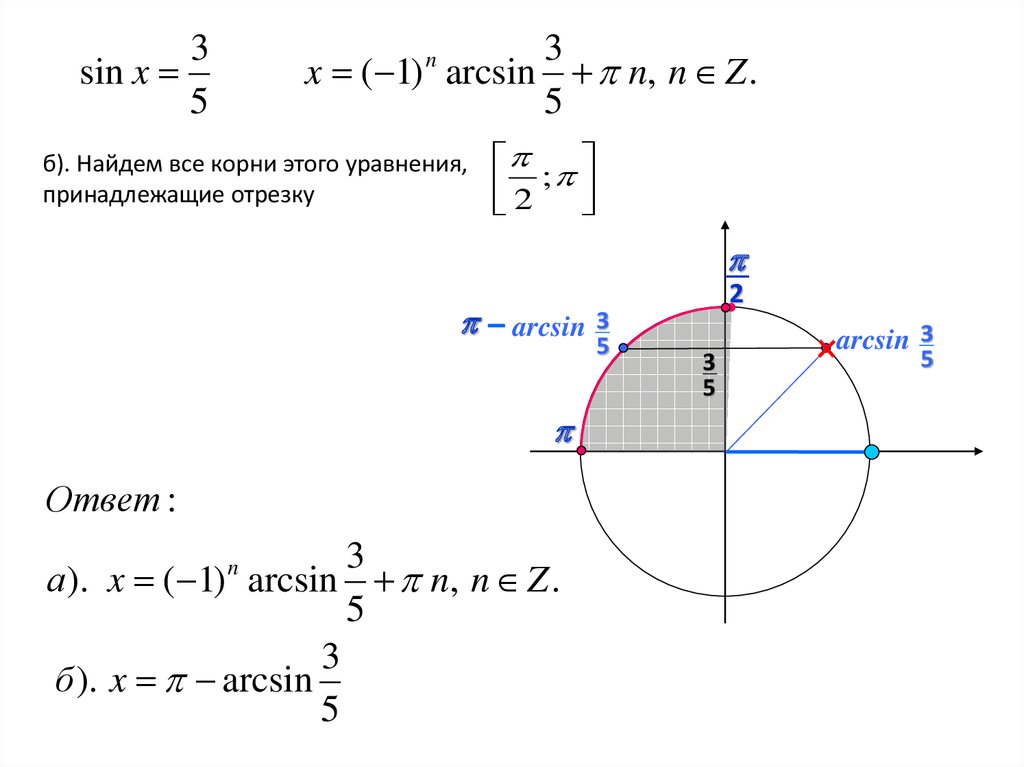
3sin x
5
3
x ( 1) arcsin n, n Z .
5
n
б). Найдем все корни этого уравнения,
;
2
принадлежащие отрезку
2
– arcsin 3
5
Ответ :
3
а ). x ( 1) arcsin n, n Z .
5
3
б ). x arcsin
5
n
3
5
arcsin 3
5
7.
а). Решите уравнение4 sin 2 х 12 sin x 5 0
б). Найдите все корни этого уравнения, принадлежащие отрезку
б). Выбирать корни по
тригонометрической окружности не
удобно, т.к. это … полтора круга
; 2
-
; 2
2
0
8.
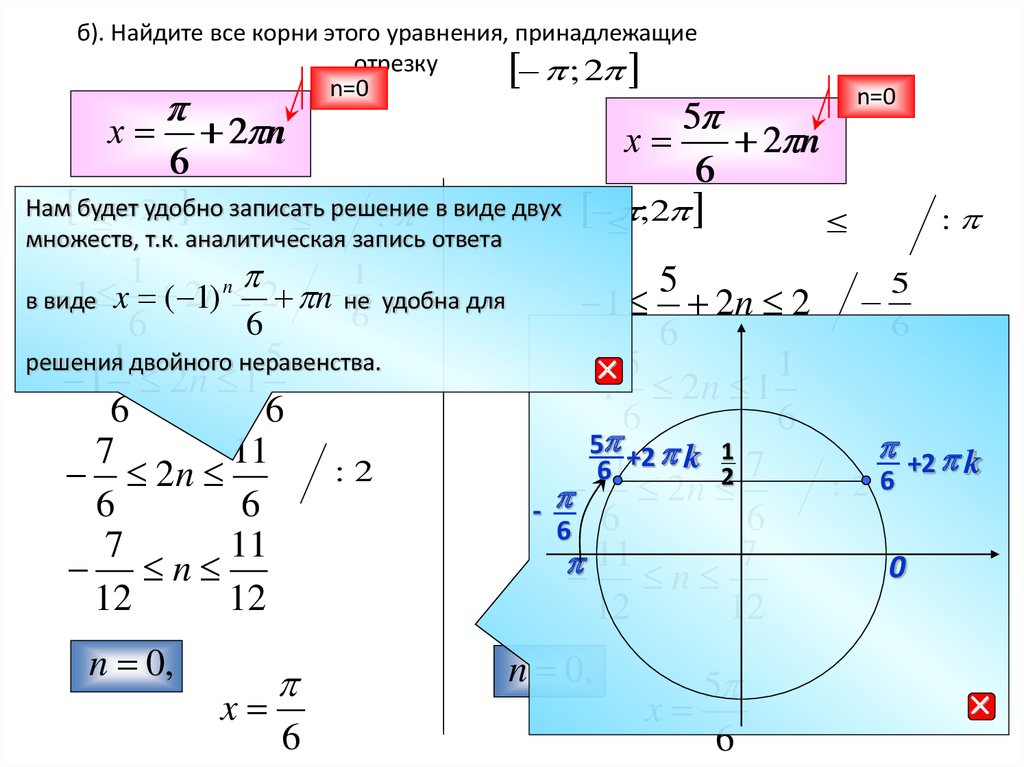
б). Найдите все корни этого уравнения, принадлежащиеотрезку
; 2
n=0
х
6
2 n
Нам будет
удобно
записать решение
; 2
: в виде двух
множеств, т.к. аналитическая запись ответа
1
1
n
1
2
n
2
n не удобна для
в виде x ( 1)
6
6
6
1двойного неравенства.
5
решения
1 2n 1
6
6
7
11
:2
2n
6
6
7
11
n
12
12
n 0,
x
6
-
5
х
2 n
6
;2
5
1 2n 2
6
5
1
1 2n 1
6
6
5 +2
1
k
11
6
2 7
2n
6
6 6
11 n 7
12
12
n 0,
n=0
5
x
6
:
:2
5
6
+2 k
6
0
9.
17tg x
1 0
cos x
2
6 sin x cos x 1 0
2
cos 2 x sin x 0,25
2
2
5
;
2
2 ; 3
5
; 2
10.
17tg x
1 0
cos x
5
;
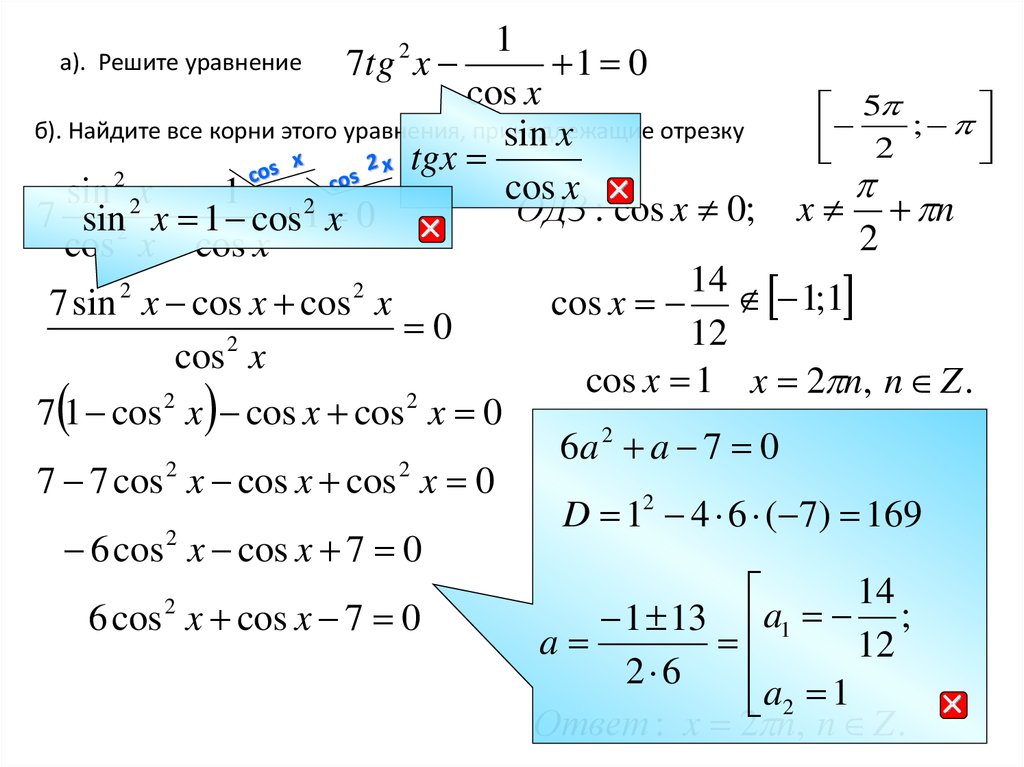
б). Найдите все корни этого уравнения, принадлежащие
отрезку
sin x
2
tgx
cos x
sin 2 2x
1
2
ОДЗ : cos x 0; x n
7 sin2 x 1 cos
1 x 0
2
cos x cos x
14
2
2
7 sin x cos x cos x
cos x 1;1
0
12
2
cos x
cos x 1 x 2 n, n Z .
2
2
7 1 cos x cos x cos x 0
2
6
a
a 7 0
2
2
7 7 cos x cos x cos x 0
2
D
1
4 6 ( 7) 169
2
6 cos x cos x 7 0
14
2
1 13 a1 ;
6 cos x cos x 7 0
a
12
2 6
a2 1
Ответ : x 2 n, n Z .
а). Решите уравнение
2
11.
б). Найдите все корни этого уравнения, принадлежащиеотрезку
n=-1
х 2 n
5
;
2
:
5
2n 1
2
5
1
n
4
2
n 1,
:2
x 2
Ответ : а ). x 2 n, n Z ,
б ) 2 .
5
;
2
12.
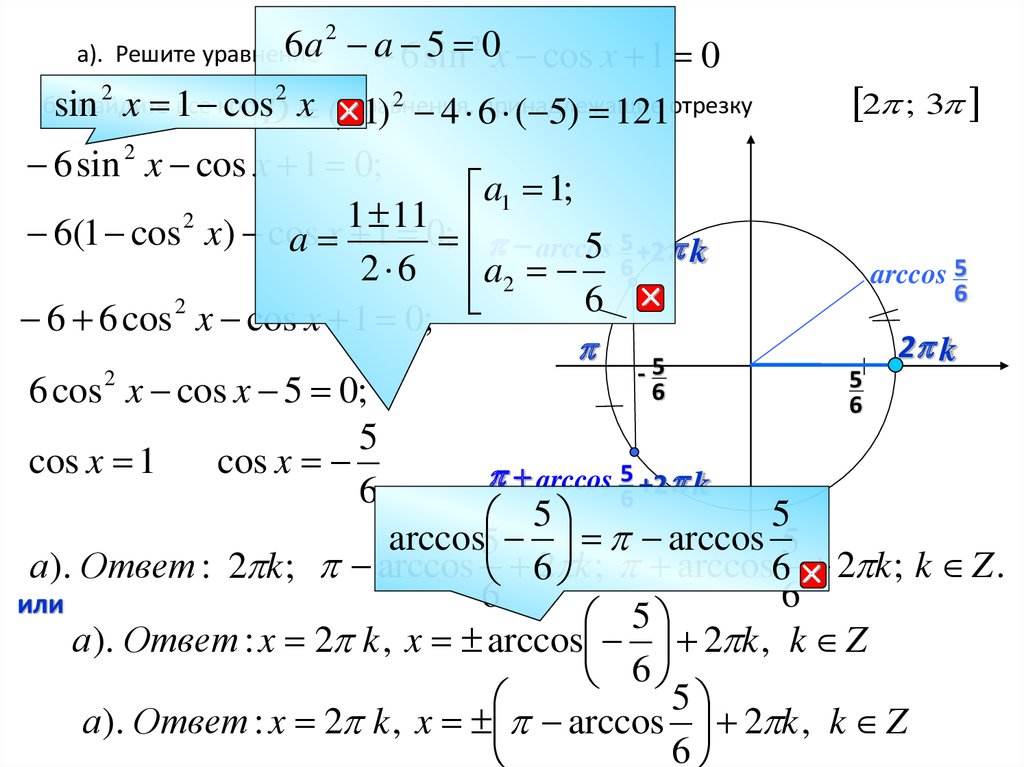
а).2
6
a
a 6 sin
5 20x cos x 1 0
Решите уравнение
б).
Найдите
sin
x 1все корни
cosDэтого
x ( уравнения,
1) 2 4 6принадлежащие
( 5) 121отрезку
2
2
2 ; 3
6 sin 2 x cos x 1 0;
a1 1;
1 111
6(1 cos 2 x) cos
x
0 ; arccos
5 +2 k
a
5
2 6 a2 6
6
2
6 6 cos x cos x 1 0;
6 cos 2 x cos x 5 0;
5
cos x
cos x 1
6
-5
6
arccos 5 +2 k
6
arccos 5
6
5
6
2 k
5
5
arccos5 arccos 5
а ). Ответ : 2 k ; arccos 62 k ; arccos6 2 k ; k Z .
6
6
или
5
а ). Ответ : x 2 k , x arccos 2 k , k Z
6
5
а ). Ответ : x 2 k , x arccos 2 k , k Z
6
13.
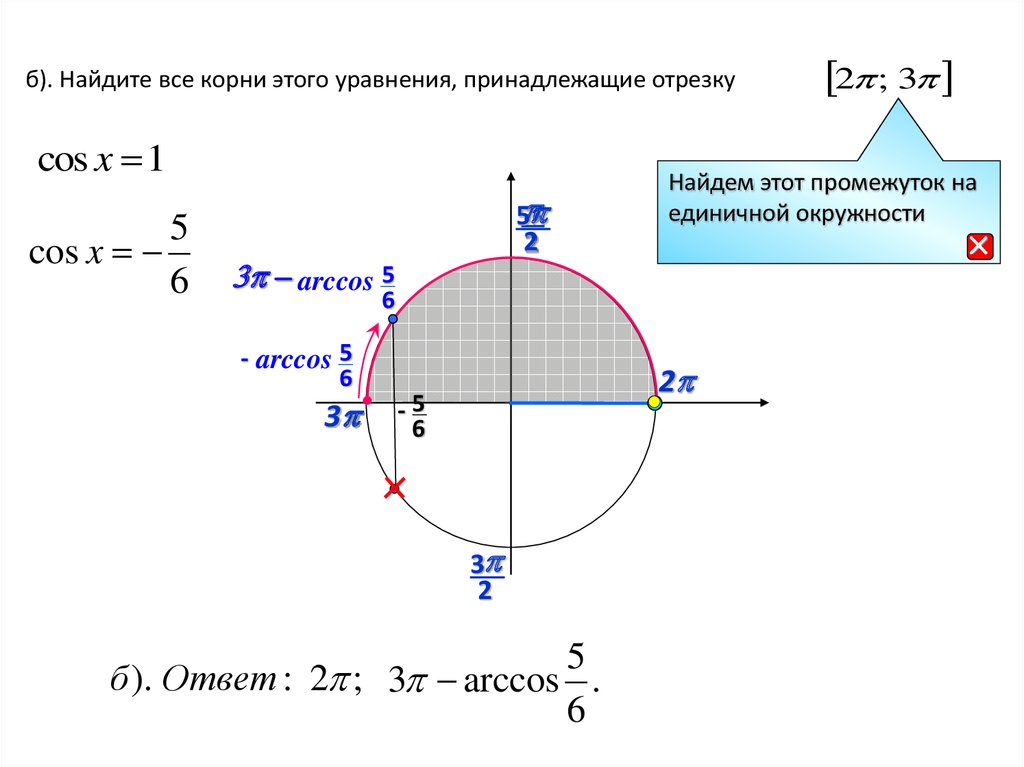
б). Найдите все корни этого уравнения, принадлежащие отрезкуcos x 1
5
cos x
6
5
2
3 arccos 5
Найдем этот промежуток на
единичной окружности
6
- arccos 5
6
3
2
-5
6
3
2
5
б ). Ответ : 2 ; 3 arccos .
6
2 ; 3
14.
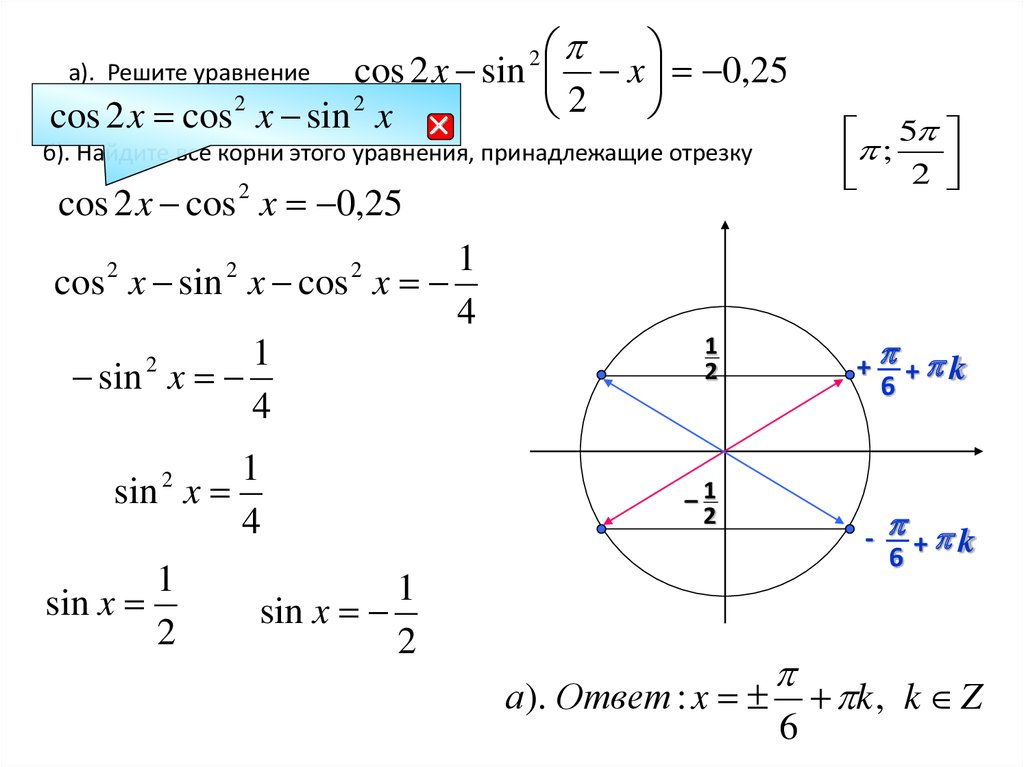
а). Решите уравнениеcos 2 x sin x 0,25
2
cos 2 x cos 2 x sin 2 x
2
б). Найдите все корни этого уравнения, принадлежащие отрезку
cos 2 x cos 2 x 0,25
1
cos x sin x cos x
4
1
2
sin x
4
2
2
2
1
sin x
4
2
1
sin x
2
5
; 2
+ + k
6
1
2
–1
2
1
sin x
2
а ). Ответ : x
-
6
k
+
6
k , k Z
15.
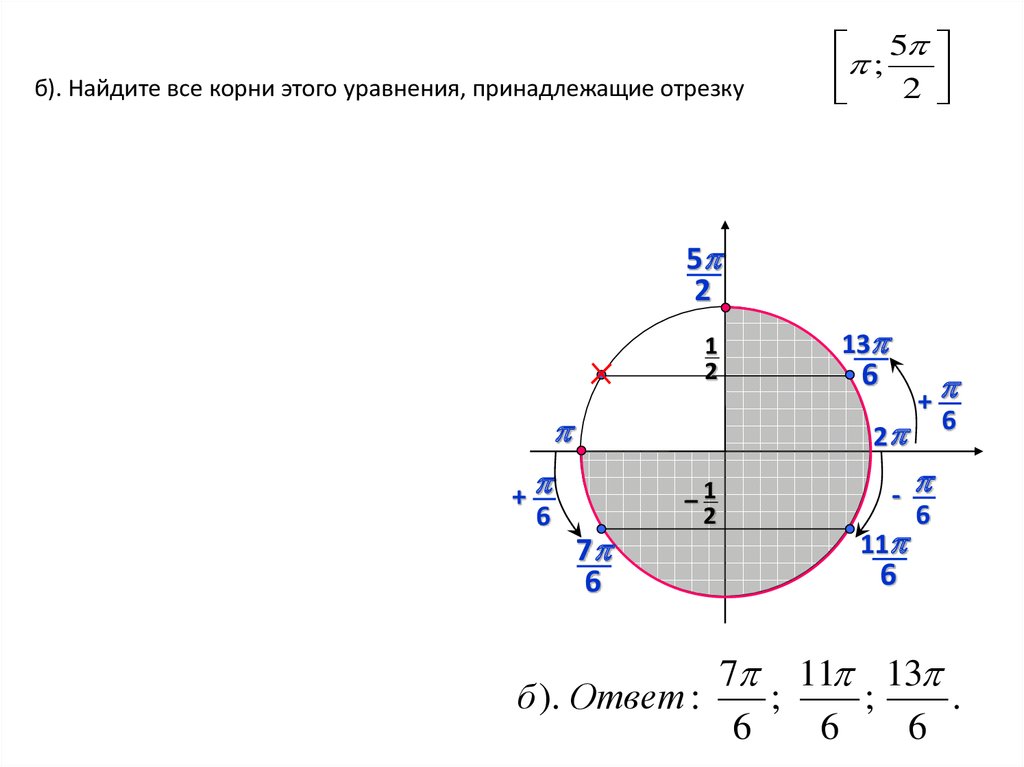
б). Найдите все корни этого уравнения, принадлежащие отрезку5
; 2
5
2
1
2
+
6
13
6
2
7
6
–1
2
11
+
6
6
6
7 11 13
б ). Ответ :
;
;
.
6
6
6
16. Решение тригонометрического уравнения с последующим выбором корней из заданного промежутка эксперты оценивают выполнение
задания по следующимкритериям:
- обоснованно получены ответы в обоих
пунктах – 2 балла (это макс. балл);
- обосновано решение в пункте а или б –
1 балл;
- решение не соответствует ни одному из
критериев, перечисленных выше – 0 баллов.
17. «Вы - талантливые дети! Когда – нибудь вы сами приятно поразитесь, какие вы умные, как много вы сумеете, если будете постоянно
работать над собой…»Жан-Жак Руссо
18.
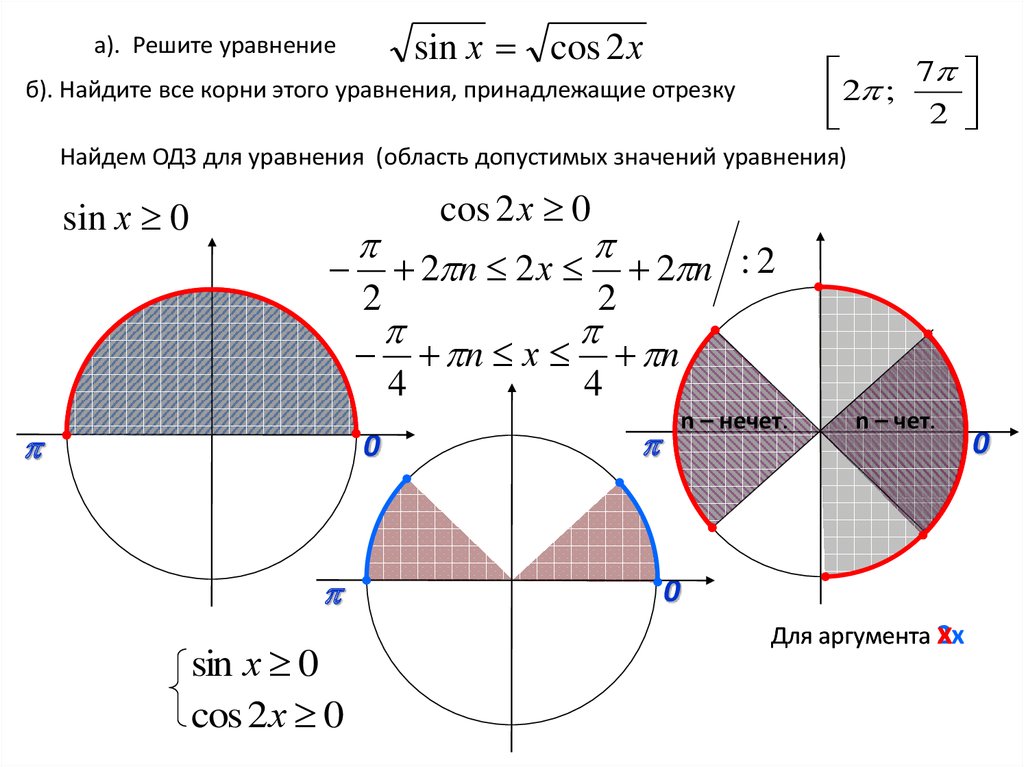
sin х cos 2 ха). Решите уравнение
7
2
;
2
б). Найдите все корни этого уравнения, принадлежащие отрезку
Найдем ОДЗ для уравнения (область допустимых значений уравнения)
sin х 0
sin х 0
cos 2х 0
2 n 2 х
2 n : 2
2
2
n х n
4
4
0
cos 2 х 0
n – нечет.
n – чет.
0
Для аргумента х
2х
0
19.
Отбор корней с помощью решения неравенств7
2 ; 2
б). Найдите все корни этого уравнения, принадлежащие отрезку
n=1
х 2 n
6
7
2 ;
2
1
7
1
2 2n
6
6
2
11
20
:2
2n
6
6
11
20
n
12
12
13
n 1, x
6
:
5
2 n
х
6
7
2
;
2
5
7
2 2n
6
2
7
16
2n
6
6
n=1
:
5
6
:2
7
16
n
12
12
n 1,
17
x
6
20.
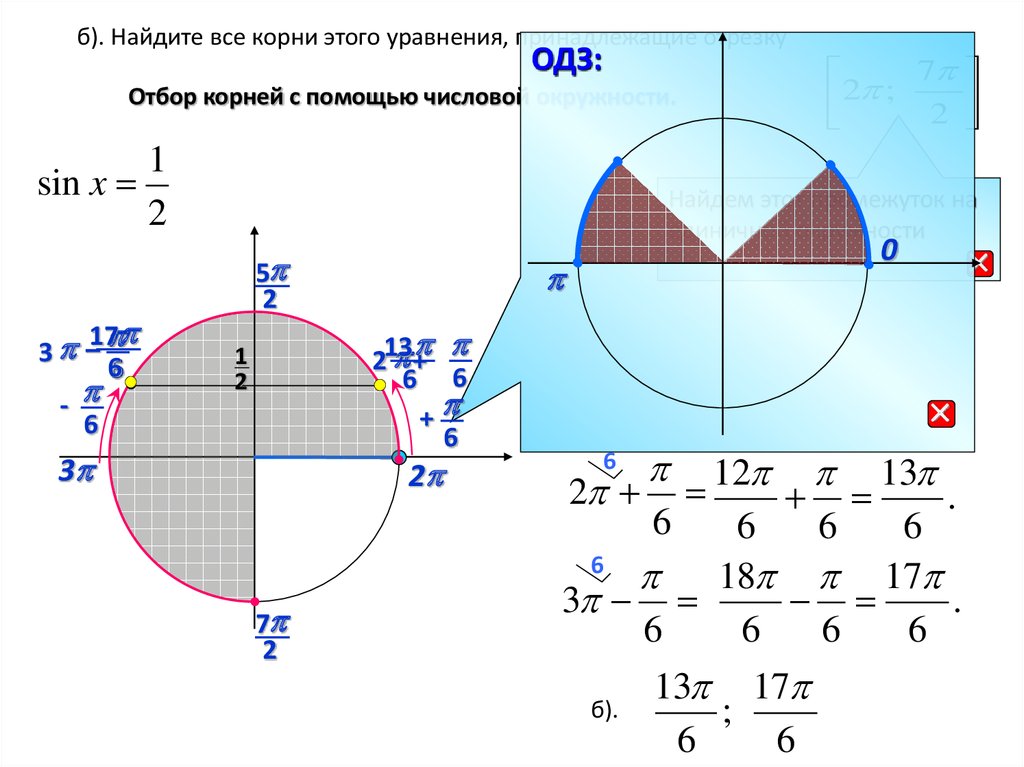
б). Найдите все корни этого уравнения, принадлежащие отрезкуОДЗ:
Отбор корней с помощью числовой окружности.
1
sin x
2
17
3 –
6
-
6
7
2
;
2
Найдем этот промежуток на
единичной окружности
5
2
+
213
6 6
+
6
1
2
3
2
7
2
0
12 13
.
6
6
6
6
6
18 17
3
.
6
6
6
6
6
2
б).
13 17
;
6
6

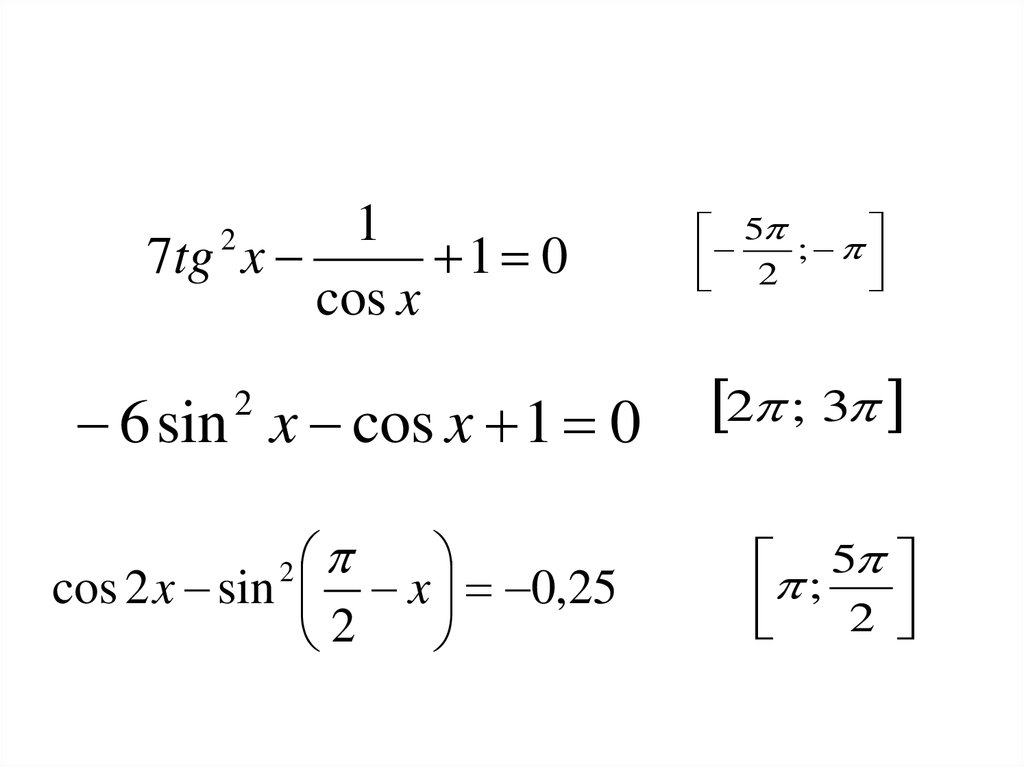




 Математика
Математика