Роль Н.И. Лобачевского в российской математике и образовании

1.

ГОСУДАРСТЕННОЕ БЮДЖЕТНОЕ ОБЩЕОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ГОРОДА МОСКВЫ
СРЕДНЯЯ ОБЩЕОБРАЗОВАТЕЛЬНАЯ ШКОЛА №1000
Роль Н.И. Лобачевского в российской
математике и образовании
Когда-то Лобачевский думал,
Кутаясь в пальто,
Как мир прямолинеен,
Видно, что-то здесь не то.
Но он вгляделся пристальней
В безоблачную высь,
А там все параллельные его
пересеклись.
Автор: ученица 9 класса «А», Афанасьева Ирина
Научный руководитель: учитель математики,
Полункина Светлана Николаевна

2.

Все! Перечеркнуты “Начала”.
Довольно мысль на них скучала,
Хоть прав почти во всем Евклид,
Но быть не вечно постоянству:
И плоскость свернута в пространство,
И мир
Иной имеет вид...

3.

Прежде чем приступить к исследованию, мы
решили провести социологический опрос.
Ученикам 9-х классов ГБОУ СОШ №1000
были заданы 3 вопроса:
1.Сформулируйте аксиому параллельных
прямых.
2. Что вы знаете о геометрии Лобачевского?
3. Что вы знаете о геометрии Евклида?

4.

25
20
Получен верный
полный ответ
Ответ не получен
или неверный
15
10
5
0
Геометрия
Лобачевского
Геометрия
Евклида

5.

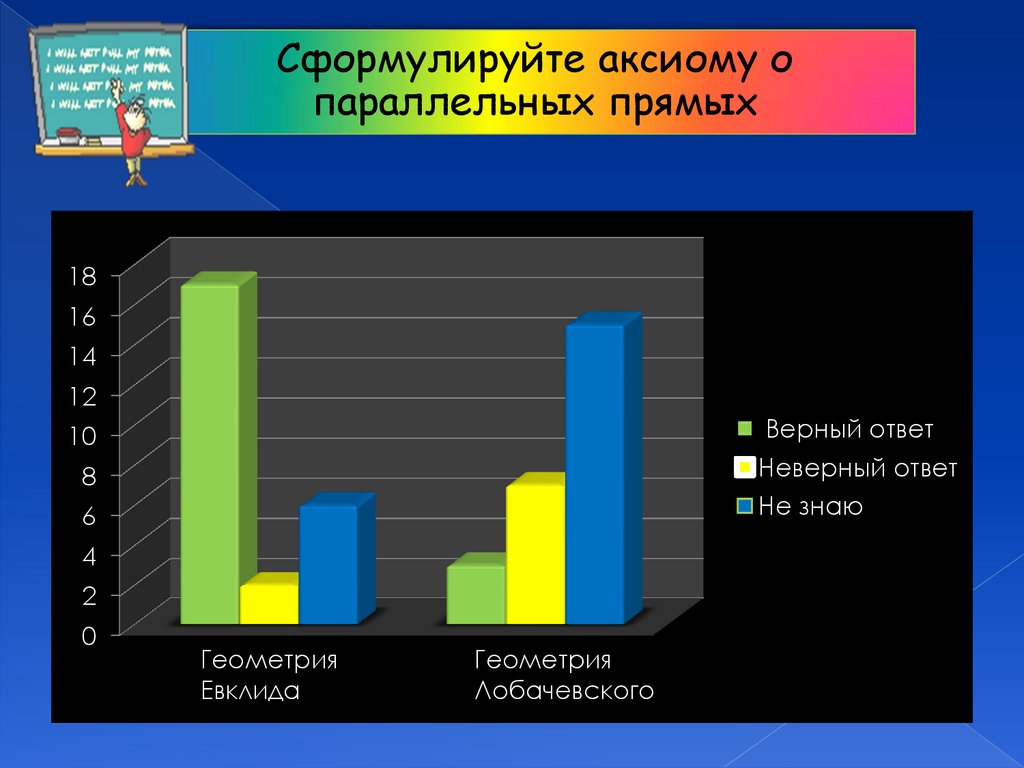
Сформулируйте аксиому о
параллельных прямых
18
16
14
12
Верный ответ
10
Неверный ответ
8
Не знаю
6
4
2
0
Геометрия
Евклида
Геометрия
Лобачевского

6.

История создания геометрии Лобачевского
одновременно является историей попыток доказать
пятый постулат Евклида. Пятый постулат – последнее
и самое сложное из предложений, включённых
Евклидом в его аксиоматику геометрии, поэтому его
часто заменяют эквивалентной ему аксиомой
параллельных прямых.
В конце 18 века у некоторых геометров возникла мысль о
невозможности доказать пятый постулат.
Решение этого вопроса было найдено великим русским
математиком Н.И, Лобачевским. Он предпринял попытку доказать
от противного: он предположил, что через данную точку, не
лежащую на данной прямой, можно провести несколько прямых,
не пересекающих данную. Тем самым пятый постулат Евклида
был доказан.

7.

Аксиома
Лобачевского о
параллельных
прямых
Через точку, не лежащую
на данной прямой,
проходят по крайней мере
две прямые, лежащие с
данной прямой в одной
плоскости и не
пересекающие её.
Аксиома Евклида о
параллельных
прямых
Через точку, не лежащую
на данной прямой,
проходит только одна
прямая, лежащая с данной
прямой в одной плоскости
и не пересекающая её.

8.

В геометрии Лобачевского сохраняются все теоремы, которые в
евклидовой геометрии можно доказать без пятого постулата.
Однако теоремы, при доказательстве которых
применяется
аксиома
параллельности,
видоизменяются.
Например, в геометрии Лобачевского сумма
углов меньше 180°.
В
геометрии
Лобачевского
не
существует
подобных треугольников. Более того, в этой
геометрии
существует
четвёртый
признак
равенства треугольников: если углы одного
треугольника соответственно равны углам другого
треугольника, то эти треугольники равны.
На рисунке 1 изображён интересный вариант
расположения трёх прямых на плоскости Лобачевского:
каждые две из них параллельны.

9.

Пусть AOB – острый угол (рисунок 2).
В геометрии Лобачевского можно
выбрать такую точку M на стороне OB,
что перпендикуляр MQ к OB не
пересекается с другой стороной угла.
Этот факт подтверждает, что не
выполняется пятый постулат: сумма
α и β меньше развёрнутого угла, но
OA и MQ не пересекаются. Если
начать приближать точку M к O, то
найдётся такая точка C, что
перпендикуляр CD к стороне OB всё
ещё не пересекается со стороной
OA, но для любой точки E,
лежащей между O и C
соответствующий перпендикуляр EF
пересекается с OA. Прямые OA и
CD всё более приближаются к друг
другу, но общих точек не имеют.

10.

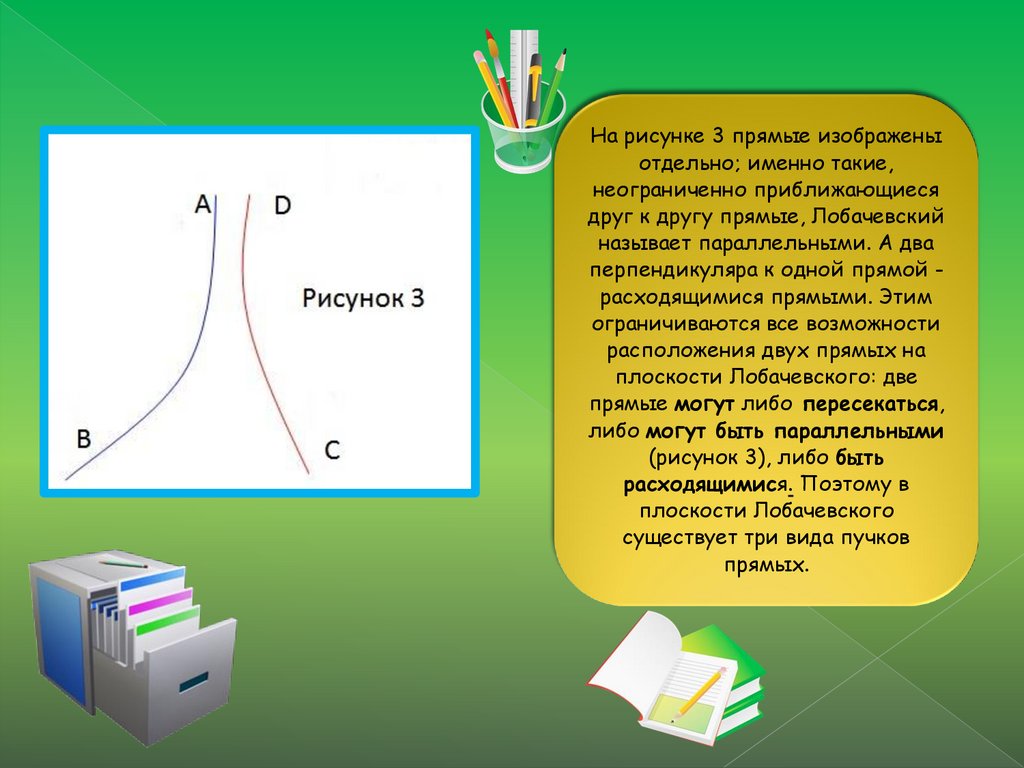
На рисунке 3 прямые изображены
отдельно; именно такие,
неограниченно приближающиеся
друг к другу прямые, Лобачевский
называет параллельными. А два
перпендикуляра к одной прямой расходящимися прямыми. Этим
ограничиваются все возможности
расположения двух прямых на
плоскости Лобачевского: две
прямые могут либо пересекаться,
либо могут быть параллельными
(рисунок 3), либо быть
расходящимися. Поэтому в
плоскости Лобачевского
существует три вида пучков
прямых.

11.

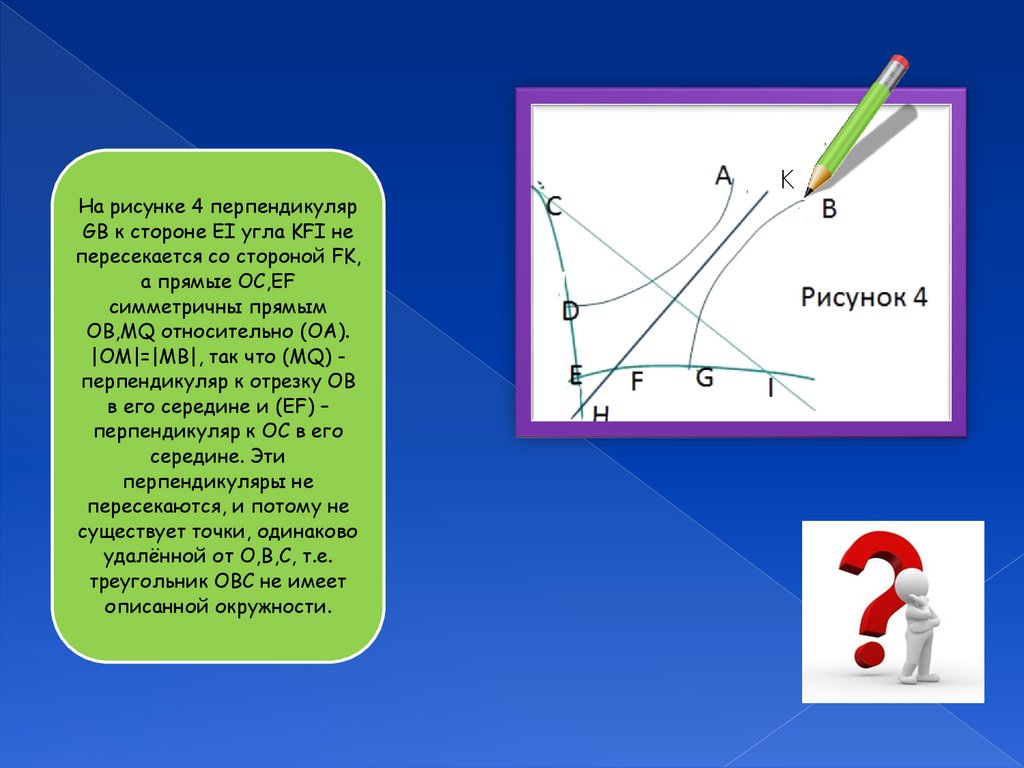
На рисунке 4 перпендикуляр
GB к стороне EI угла KFI не
пересекается со стороной FK,
а прямые OC,EF
симметричны прямым
OB,MQ относительно (OA).
|OM|=|MB|, так что (MQ) перпендикуляр к отрезку OB
в его середине и (EF) –
перпендикуляр к OC в его
середине. Эти
перпендикуляры не
пересекаются, и потому не
существует точки, одинаково
удалённой от O,B,С, т.е.
треугольник OBC не имеет
описанной окружности.
K

12.

А на рисунке 5 все прямые
параллельны друг другу в
одном направлении. Чёрная
линия «перпендикулярна»
всем проведенным
прямым. Эта линия
называется окружностью
предельной или
орициклом. Прямые
рассмотренного пучка
являются как бы её
«радиусами», а «центр»
предельной окружности
лежит в бесконечности,
поскольку «радиусы»
параллельны. В то же
время орицикл не является
прямой линией, она
«искривлена».

13.

На рис. 6 приведён «паркет», изображённый
в модели Пуанкаре (замощение плоскости
Лобачевского правильными
восьмиугольниками). Пуанкаре придумал
фантастический мир, «жители» которого
должны были бы принять геометрию
Лобачевского из физических
экспериментов. Для этого Пуанкаре
предположил, что круг С представляет
собой неоднородную оптическую среду, в
которой скорость света в точке A Є С равна
расстоянию точки А от границы круга С.
Тогда свет будет распространяться как раз
по «прямым» рассмотренной модели. Свет
не может за конченое время дойти до
границы, и поэтому этот мир будет
восприниматься его «жителями»
бесконечным, причём по своим свойствам,
совпадающим с плоскостью Лобачевского.
Жюль Анри́ Пуанкаре́ французский математик, физик,
астроном и философ
.
А

14.

Предлагаем Вашему вниманию
несколько заданий, чтобы убедиться,
что геометрия Лобачевского широко
используется на практике (в частности,
для графического представления
объёмных тел).
Вы можете их выполнить в том
случае, если уже прошли курс
геометрии 7 класса.

15.

1. Сможет ли самолёт оказаться в той же точке, если
пролетит 1 км. на юг, 1 км. на восток и 1 км. на север?
Ответ: сможет, если он вылетит с севера.
2. Параллельны ли эти прямые?
Ответ: да.
3. Параллельны ли две прямые
по центру?
Ответ: да.
4. Есть ли движение
на этой картинке?
Ответ: нет
5. Равны ли эти два отрезка?
Ответ: да.

16.

Вывод: В геометрии истинность
каждого утверждения надо
доказывать, нельзя полагаться
только на интуицию и наблюдения.
Положительный момент: благодаря
зрительным искажениям существует
живопись.
Сальвадор Дали. Пятьдесят абстрактных картин,
складывающихся на расстоянии два метра в
три портрета Ленина в виде китайца, а с шести
метров превращающихся в голову
королевского тигра. Этюд

17.

Н. Лобачевский стал магистром в 19 лет, а в 24 года –
профессором.
Однажды в школе Лобачевский прибил гвоздём к учительскому столу классный
журнал. Учитель быстро нашёл виновного, после чего вскочил с места и произнёс:
«Лобачевский, ты станешь разбойником!». Когда Коля вырос и стал ректором,
старенький учитель пришёл к нему с просьбой о помощи. Добродушно улыбаясь,
Лобачевский напомнил ему: «А помните, как вы мне пророчили, что я стану
разбойником. К счастью, этого не произошло». И он с удовольствием помог ему.
Лобачевскому было всего 34 года, когда он решил
«многовековую» проблему V постулата из «Начал»
Евклида и построил свою, неевклидову геометрию.
Имя Лобачевского известно всему миру. Он вошёл в историю математики как
революционер в науке и «Коперник геометрии».
12 февраля 1856 года Лобачевский умер. Последние
слова, которые он произнёс: «Человек родился, чтобы
умереть». В этих словах несомненно сказалась печаль
последних одиноких лет.
В 1992 году была учреждена медаль имени Лобачевского. Её выдают каждые 5 лет
за выдающиеся достижения в исследованиях геометрии.
В 1962 году в честь знаменитого учёного, математика,
создателя неевклидовой геометрии Н. И. Лобачевского
была названа улица в Западном административном
округе Москвы