Похожие презентации:
Многогранники
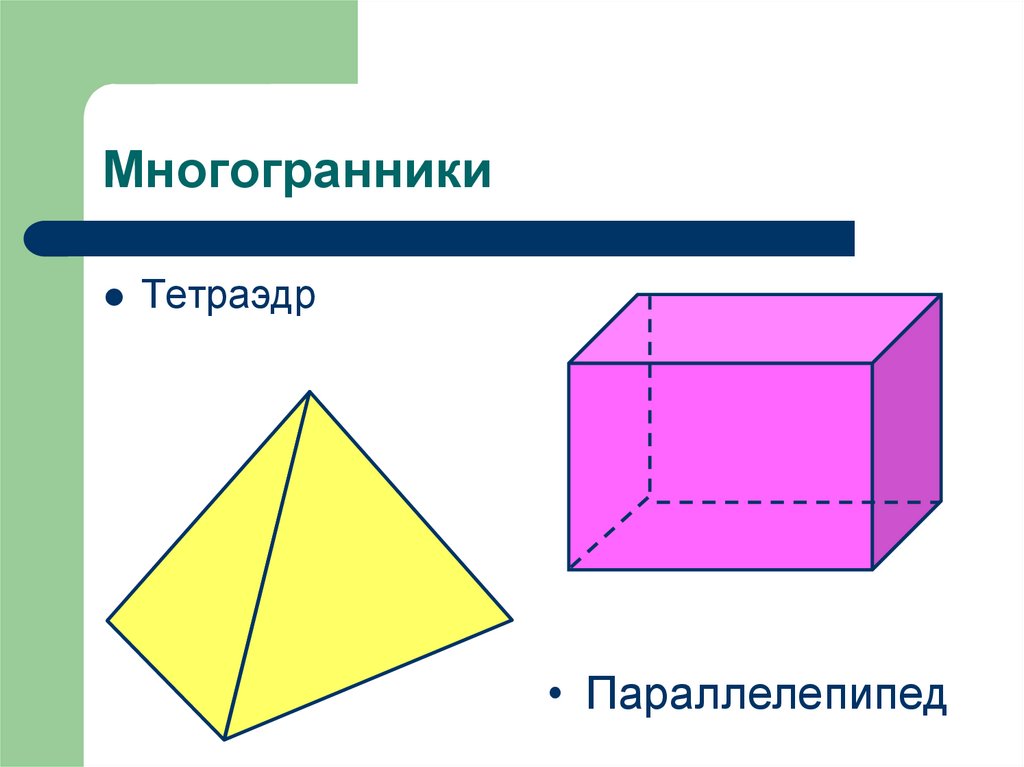
1. Многогранники
Тетраэдр• Параллелепипед
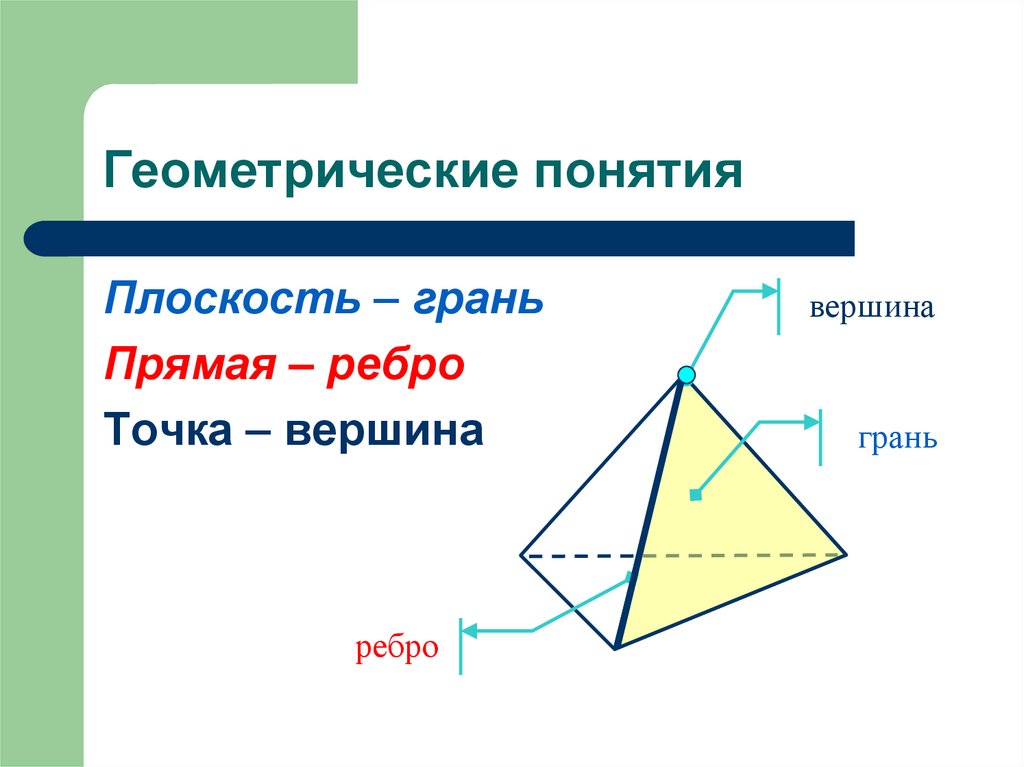
2. Геометрические понятия
Плоскость – граньПрямая – ребро
Точка – вершина
ребро
вершина
грань
3. Кроссворд
6М
1
П
Л
О
С
К
О
С
Т
Ь
Г5
Т3
Р
2 О
4
В
Р
А
Е Ч Е Н
Б К Р Ь
Р А Ш
О
И
Н
А
Н
О
Г
О
Г
Р
А
Н
Н
И
К
7
С
Т
Е
Р
Е
О
М
Е
Т
Р
И
Я
1.
2.
3.
4.
5.
6.
7.
Бесконечная ровная поверхность
Сторона грани многогранника.
Основное понятие геометрии – место
пересечения двух прямых.
Точка пересечения ребер
многогранника.
Сторона многогранника.
Поверхность, составленная из
многоугольников.
Раздел геометрии, изучающий фигуры
в пространстве.
4. Построение сечений в многогранниках
5. Сегодня на уроке:
Повторим геометрические понятия иутверждения.
Сформулируем правила для построения
сечения.
Отработаем умения построения сечений.
6. Если 2 плоскости имеют общую точку, то
1Если 2 плоскости имеют общую
точку, то
А) они называются пересекающимися
Б) они пересекаются по прямой,
проходящей через эту точку
В) они параллельны
7. Если 2 плоскости имеют общую точку, то
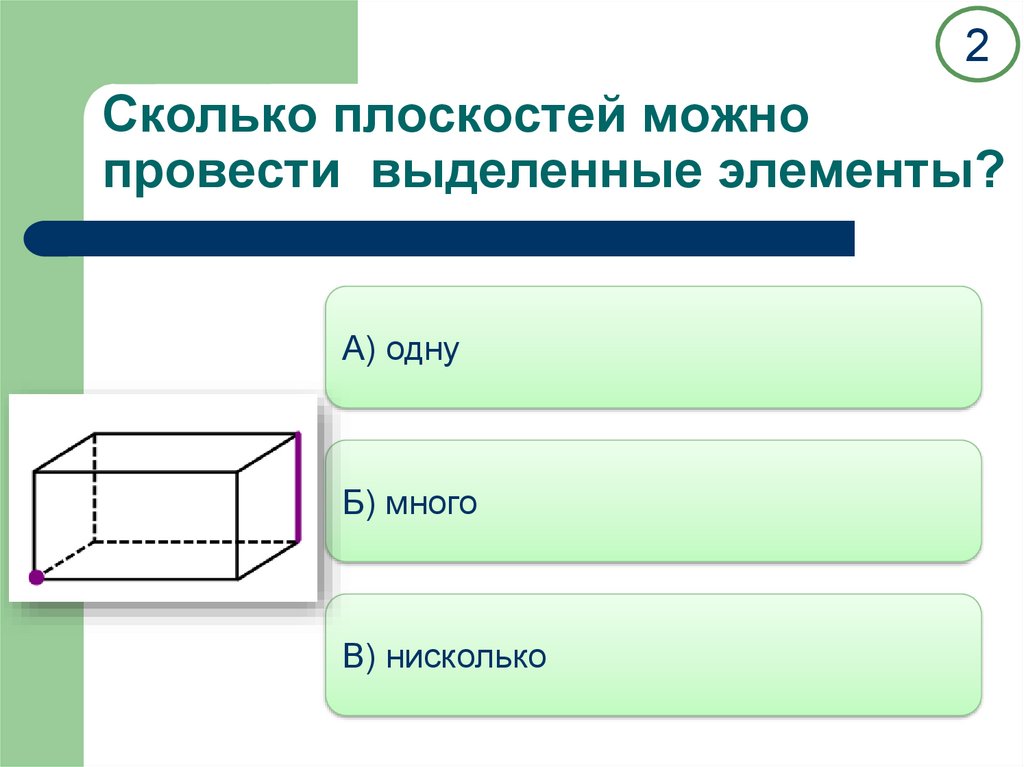
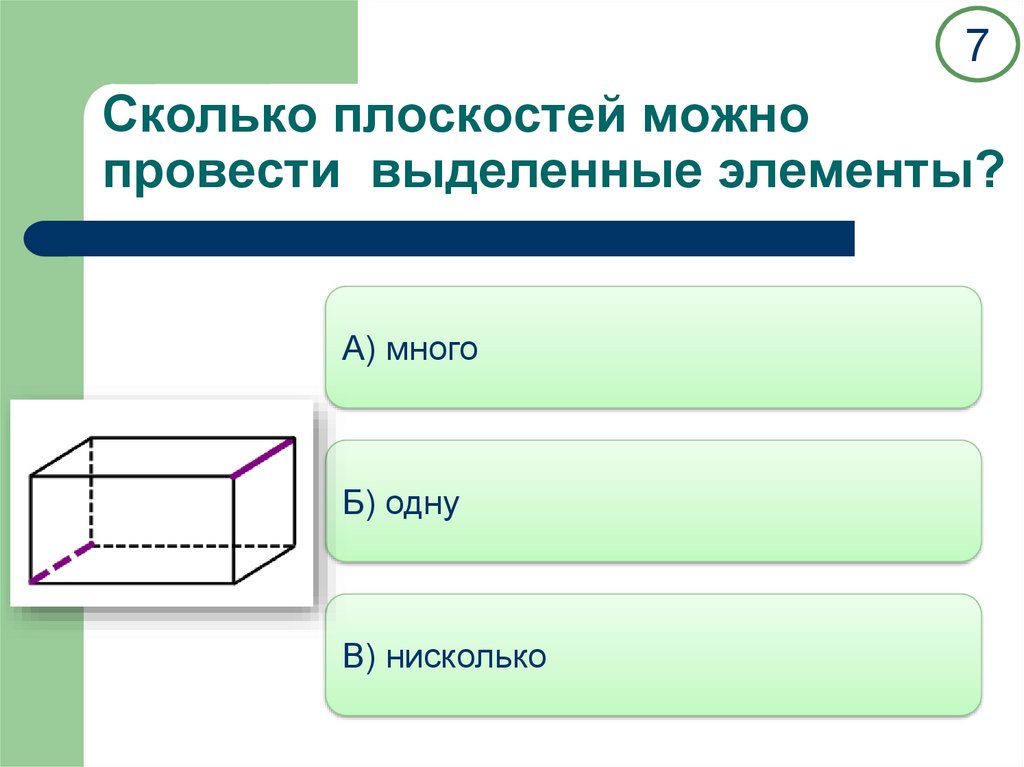
2Сколько плоскостей можно
провести выделенные элементы?
А) одну
Б) много
В) нисколько
8. Если 2 плоскости имеют общую точку, то
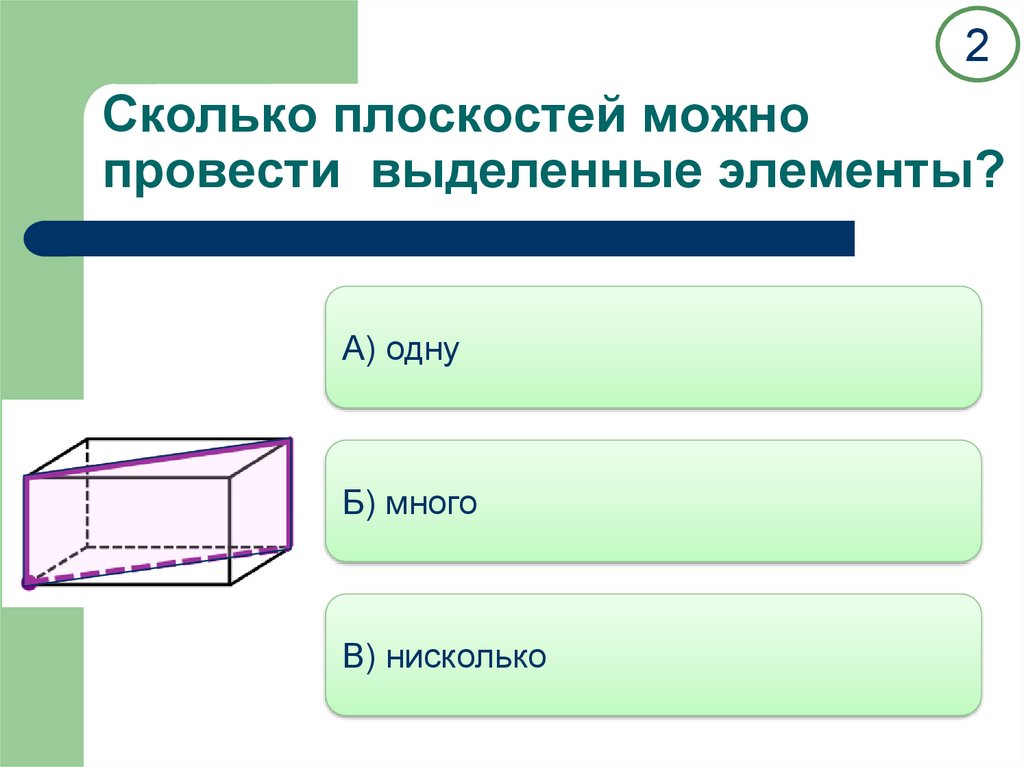
2Сколько плоскостей можно
провести выделенные элементы?
А) одну
Б) много
В) нисколько
9. Если 2 плоскости имеют общую точку, то
3Через прямую и не лежащую на
ней точку
А) проходит плоскость и притом
только одна.
Б) проходит бесконечное количество
плоскостей
В) нельзя провести плоскость
10. Сколько плоскостей можно провести выделенные элементы?
4Если прямая пересекает две
параллельные прямые, то
А) она пересекает плоскость,
образованную этими прямыми
Б) она параллельна плоскости,
образованной этими прямыми
В) она лежит в плоскости, определяемой
этими параллельными прямыми
11. Сколько плоскостей можно провести выделенные элементы?
5Две прямые называются
скрещивающимися, если
А) они лежат в одной плоскости
Б) они не пересекаются
В) они не пересекаются
и не параллельны
12. Сколько плоскостей можно провести выделенные элементы?
6Если две прямые параллельны
третей прямой, то
А) они параллельны
Б) они лежат в одной плоскости
В) они скрещиваются
13. Сколько плоскостей можно провести выделенные элементы?
7Сколько плоскостей можно
провести выделенные элементы?
А) много
Б) одну
В) нисколько
14. Через прямую и не лежащую на ней точку
8Если две точки прямой лежат в
плоскости, то
А) прямая параллельны плоскости
Б) прямая лежит в плоскости
В) прямая пересекает плоскость
15. Через прямую и не лежащую на ней точку
9Если две параллельные
плоскости пересечены третей, то
А) линии их пересечения
перпендикулярны
Б) линии их пересечении параллельны
В) линии их пересечения скрещиваются
16. Через прямую и не лежащую на ней точку
17. Через прямую и не лежащую на ней точку
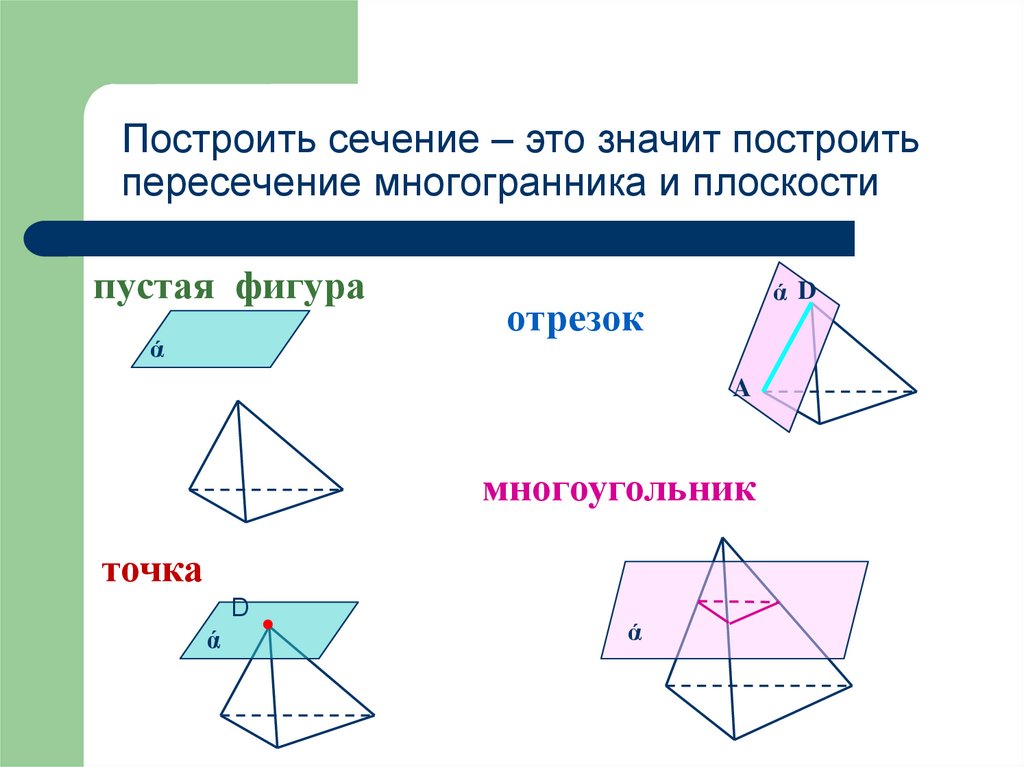
Построить сечение – это значит построитьпересечение многогранника и плоскости
пустая фигура
ά
άD
отрезок
A
многоугольник
точка
D
ά
ά
18. Если прямая пересекает две параллельные прямые, то
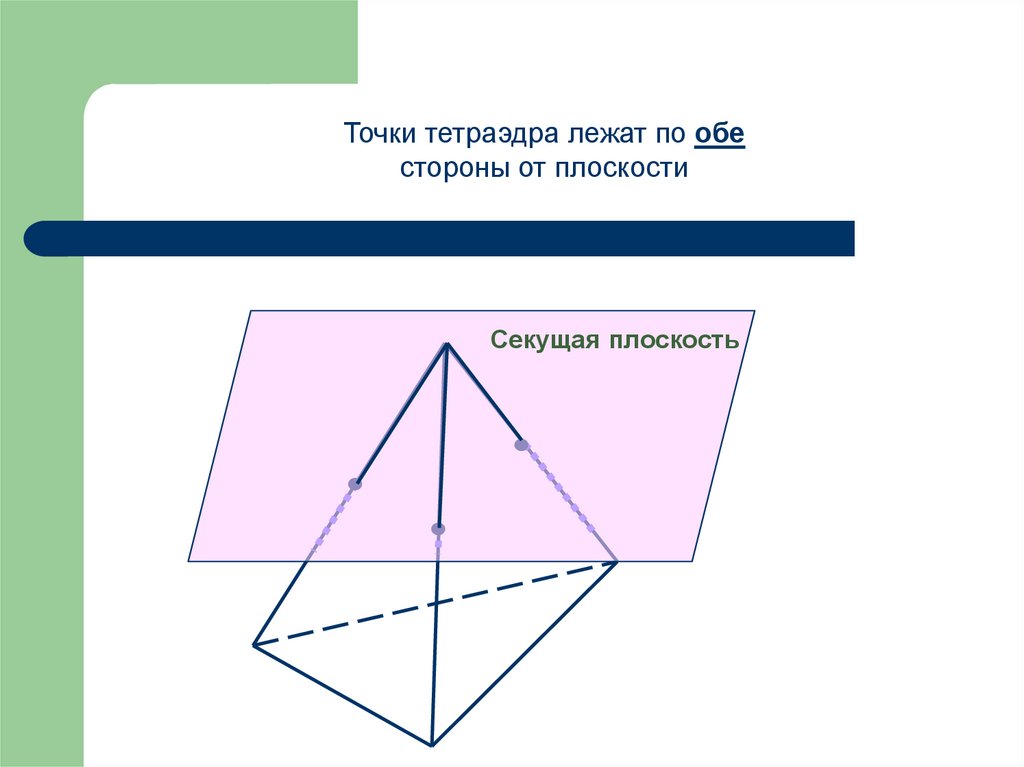
Точки тетраэдра лежат по обестороны от плоскости
Секущая плоскость
19. Если прямая пересекает две параллельные прямые, то
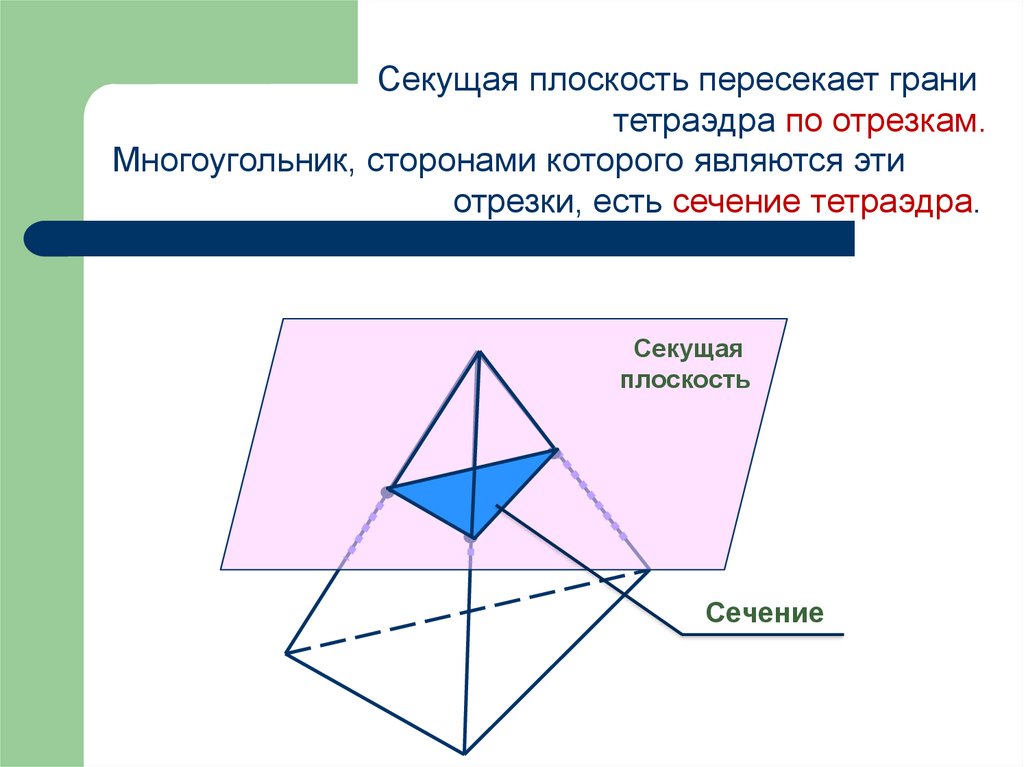
Секущая плоскость пересекает гранитетраэдра по отрезкам.
Многоугольник, сторонами которого являются эти
отрезки, есть сечение тетраэдра.
Секущая
плоскость
Сечение
20. Если прямая пересекает две параллельные прямые, то
Сечение многогранникаСечение многогранника многоугольник, вершины
которого - точки пересечения
секущей плоскости с
ребрами многогранника, а
стороны - линии пересечения
секущей плоскости с гранями
многогранника.
21. Если прямая пересекает две параллельные прямые, то
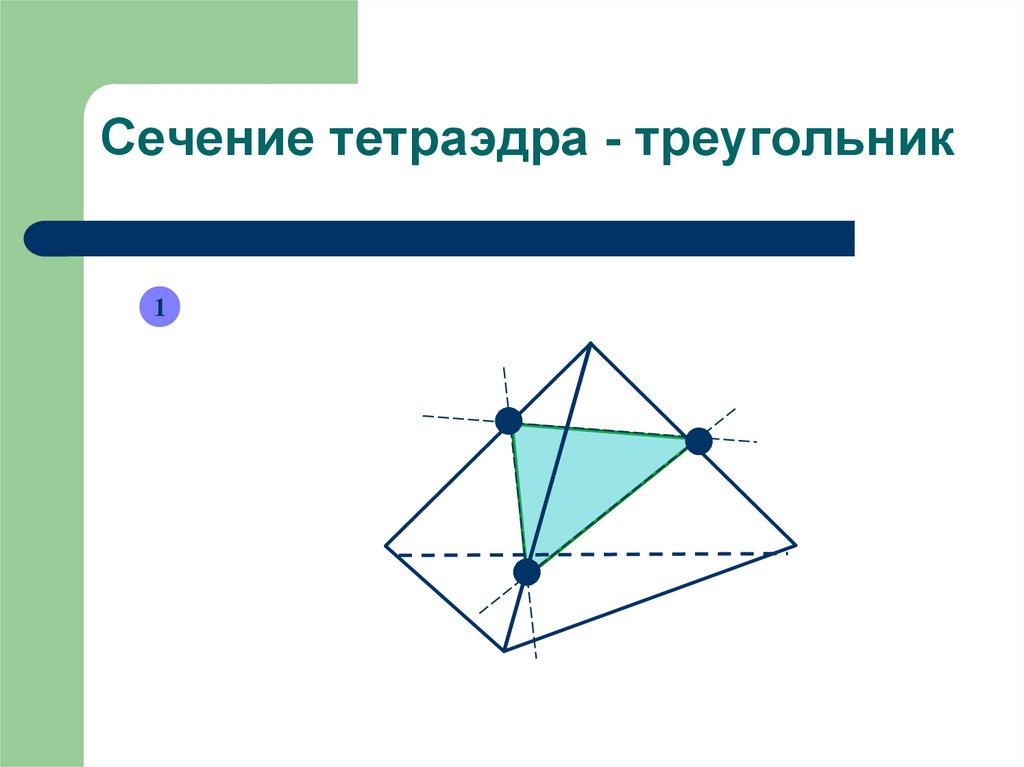
В сечение тетраэдра –треугольники и четырехугольники
22. Две прямые называются скрещивающимися, если
Сечение тетраэдра - треугольник1
23. Две прямые называются скрещивающимися, если
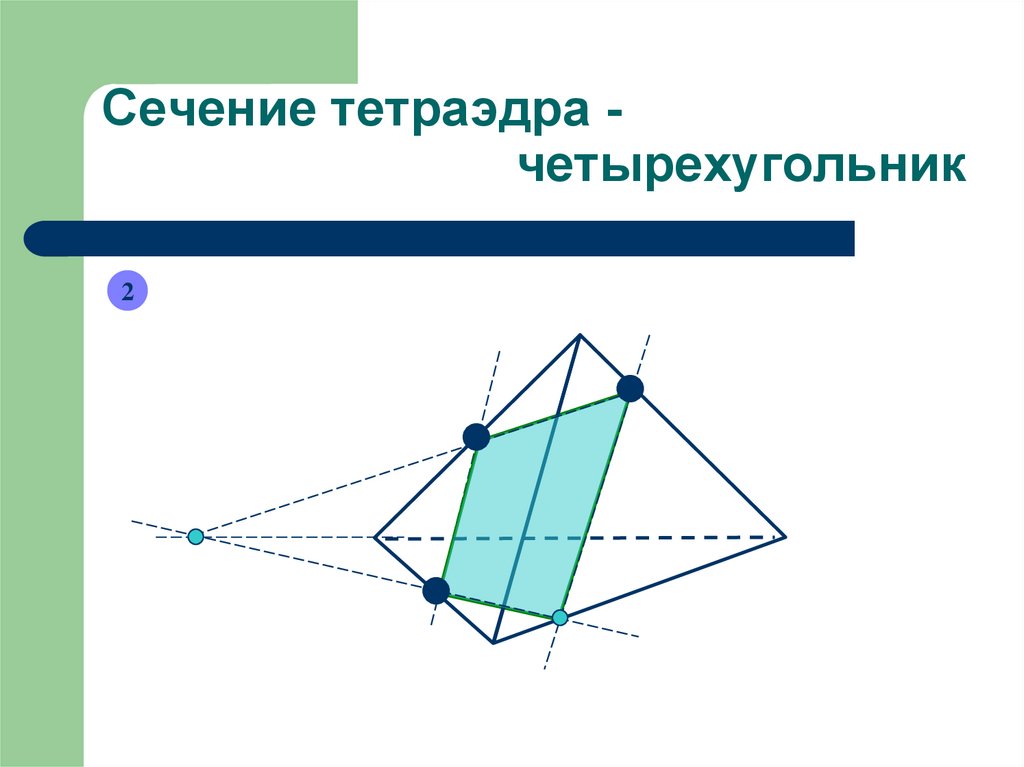
Сечение тетраэдра четырехугольник2
24. Две прямые называются скрещивающимися, если
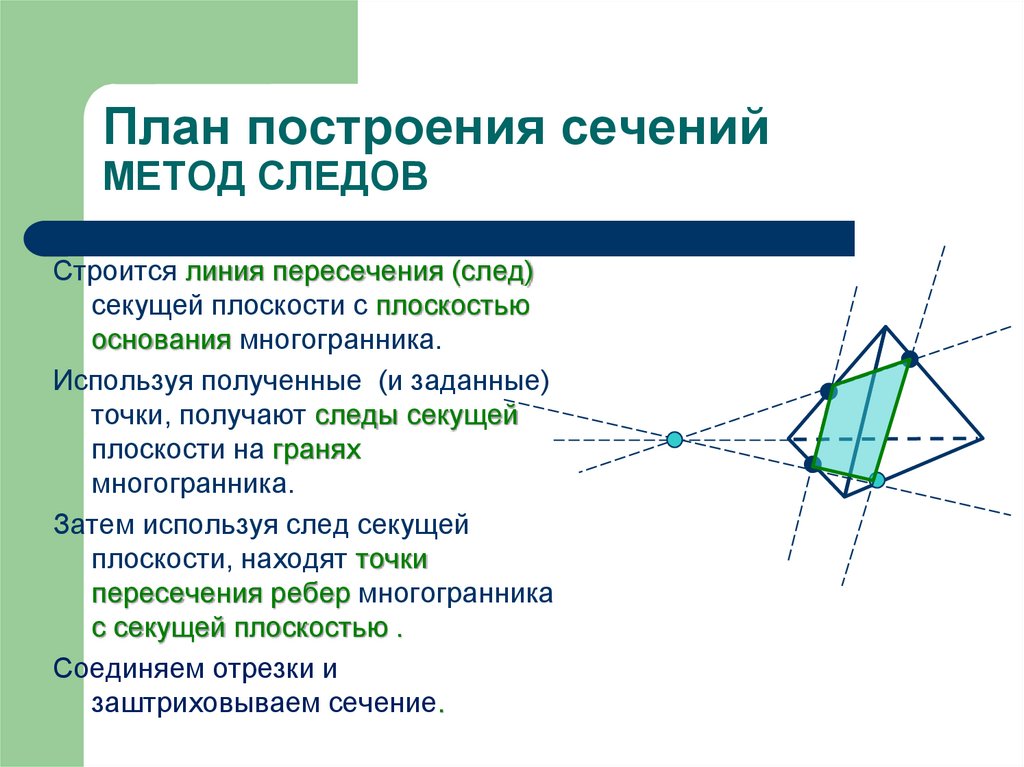
План построения сеченийМЕТОД СЛЕДОВ
Строится линия пересечения (след)
секущей плоскости с плоскостью
основания многогранника.
Используя полученные (и заданные)
точки, получают следы секущей
плоскости на гранях
многогранника.
Затем используя след секущей
плоскости, находят точки
пересечения ребер многогранника
с секущей плоскостью .
Соединяем отрезки и
заштриховываем сечение.
25. Две прямые называются скрещивающимися, если
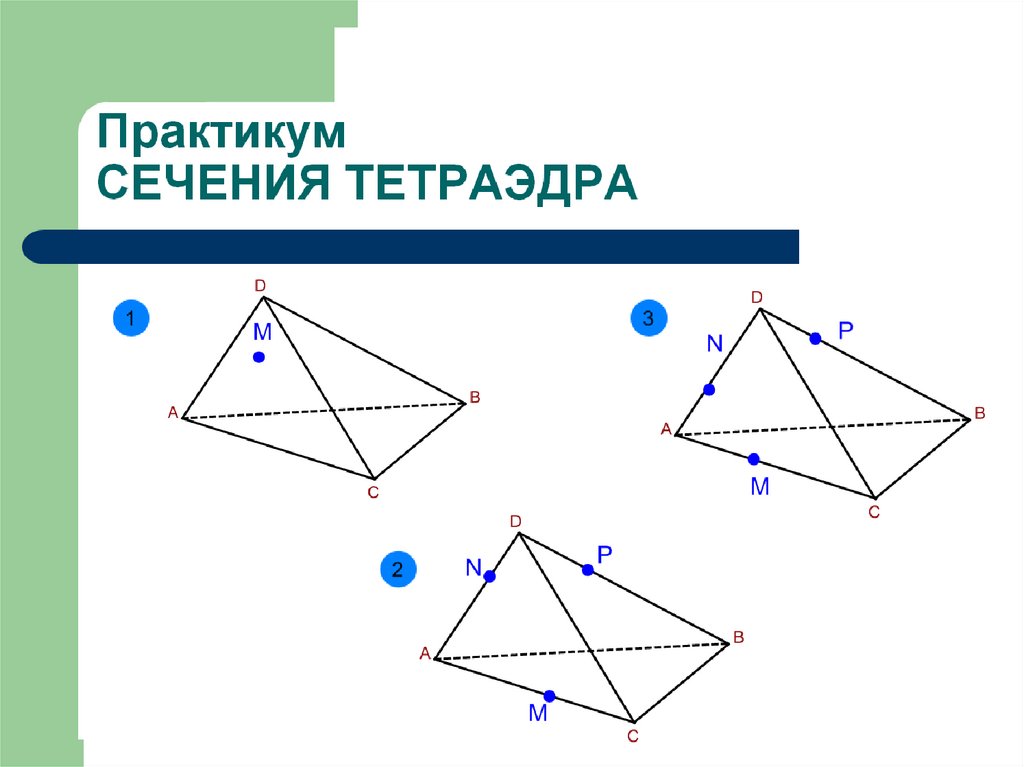
ПрактикумСЕЧЕНИЯ ТЕТРАЭДРА
26. Если две прямые параллельны третей прямой, то
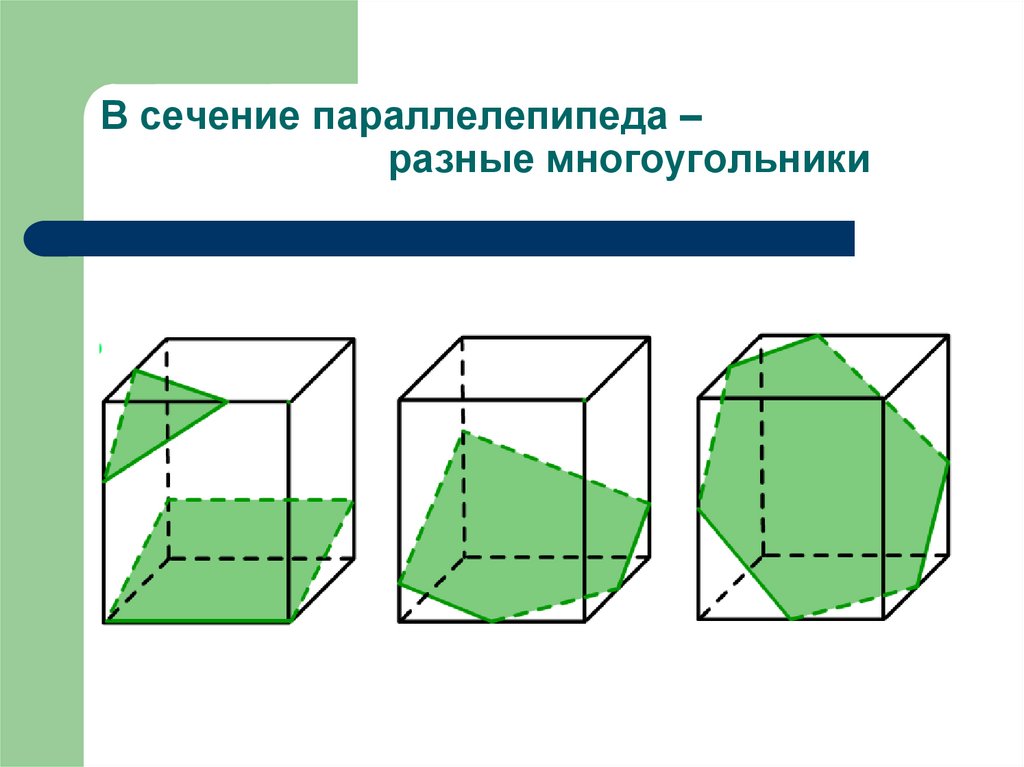
В сечение параллелепипеда –разные многоугольники
27. Если две прямые параллельны третей прямой, то
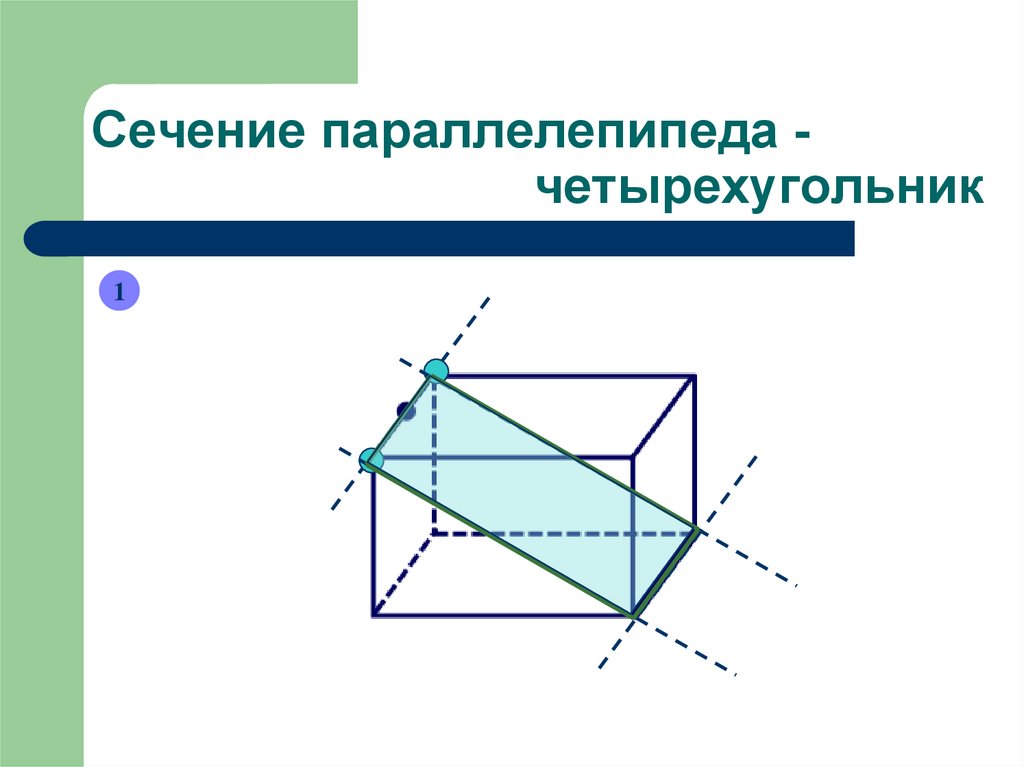
Сечение параллелепипеда четырехугольник1
28. Если две прямые параллельны третей прямой, то
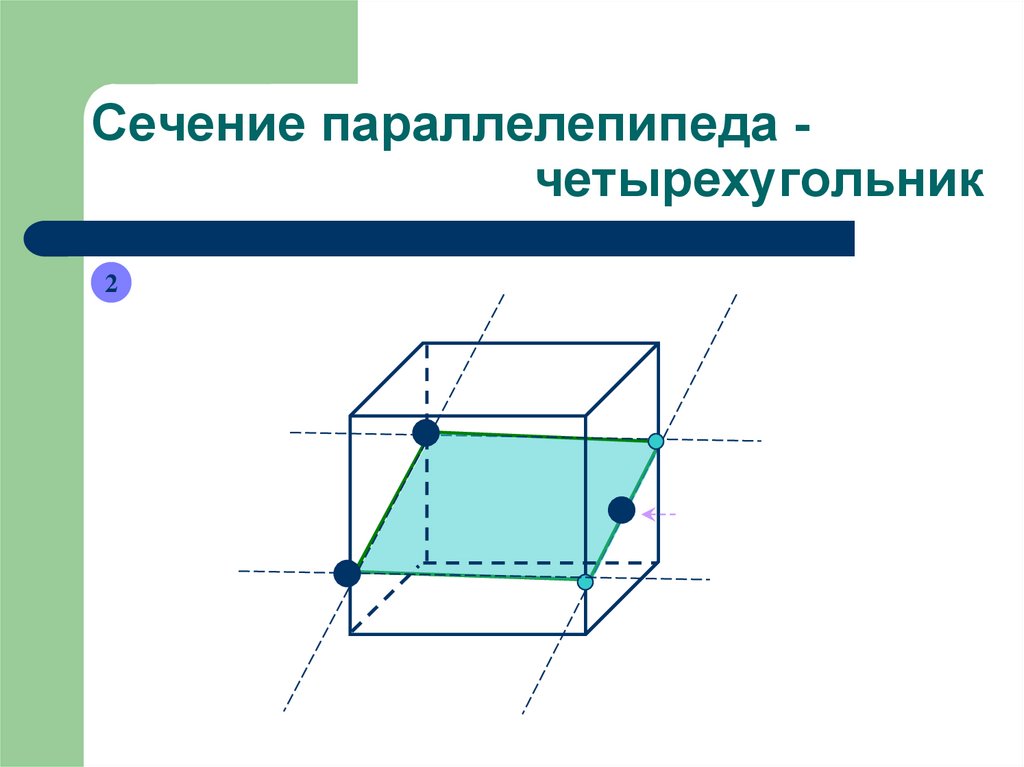
Сечение параллелепипеда четырехугольник2
29. Если две прямые параллельны третей прямой, то
План построения сечений впараллелепипеде
Соединить точки,
принадлежащие одной грани
многогранника.
В параллельных гранях
построить линии,
параллельные данным
30. Сколько плоскостей можно провести выделенные элементы?
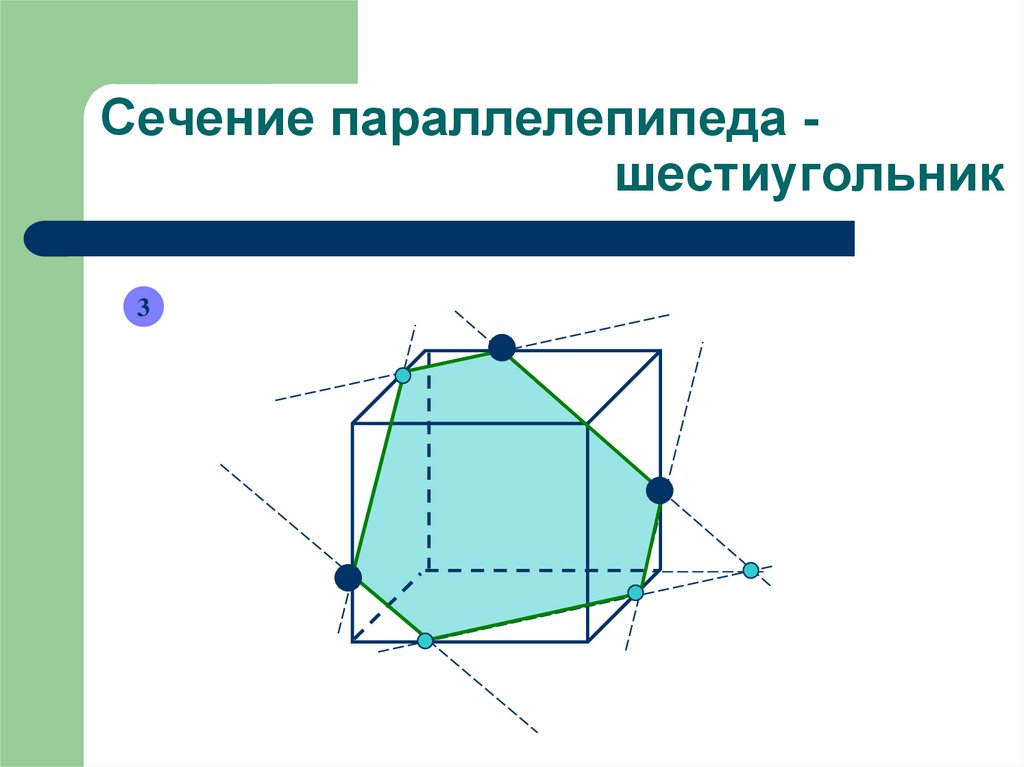
Сечение параллелепипеда шестиугольник3
31. Сколько плоскостей можно провести выделенные элементы?
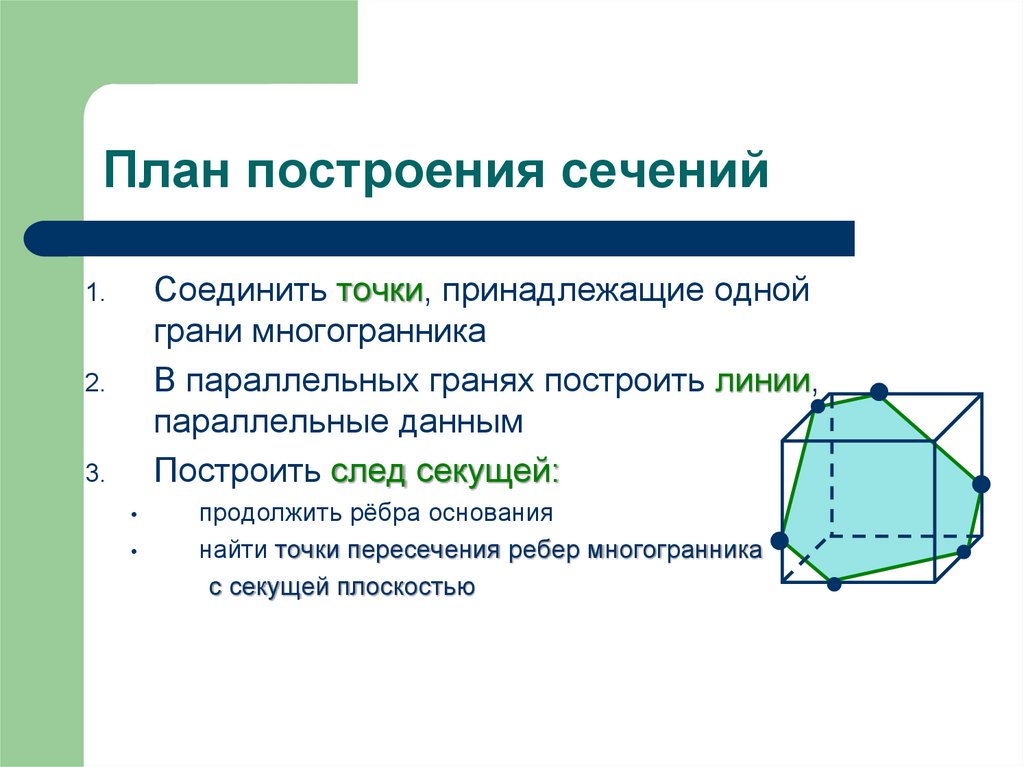
План построения сеченийСоединить точки, принадлежащие одной
грани многогранника
В параллельных гранях построить линии,
параллельные данным
Построить след секущей:
1.
2.
3.
продолжить рёбра основания
найти точки пересечения ребер многогранника
с секущей плоскостью
32. Сколько плоскостей можно провести выделенные элементы?
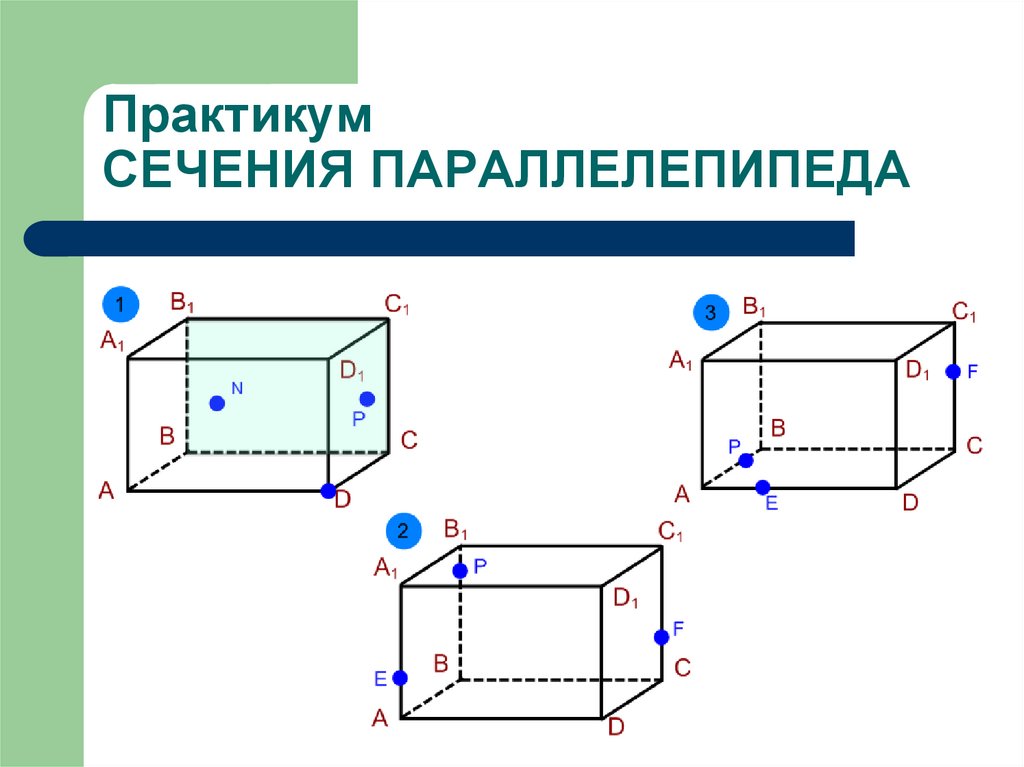
ПрактикумСЕЧЕНИЯ ПАРАЛЛЕЛЕПИПЕДА
33. Сколько плоскостей можно провести выделенные элементы?
ПРАВИЛА ПОСТРОЕНИЯСЕЧЕНИЙ
Для построения сечения достаточно построить точки
пересечения секущей плоскости с ребрами фигуры.
Через полученные точки, лежащие в одной грани,
провести отрезки.
Если невозможно соединить точки, строим след секущей
плоскости и получаем недостающие точки.
Многогранник, ограниченный данными отрезками, и есть
построенное сечение.
Если секущая плоскость пересекает противоположные
грани параллелепипеда по каким – то отрезкам, то эти
отрезки – параллельны.
34. Если две точки прямой лежат в плоскости, то
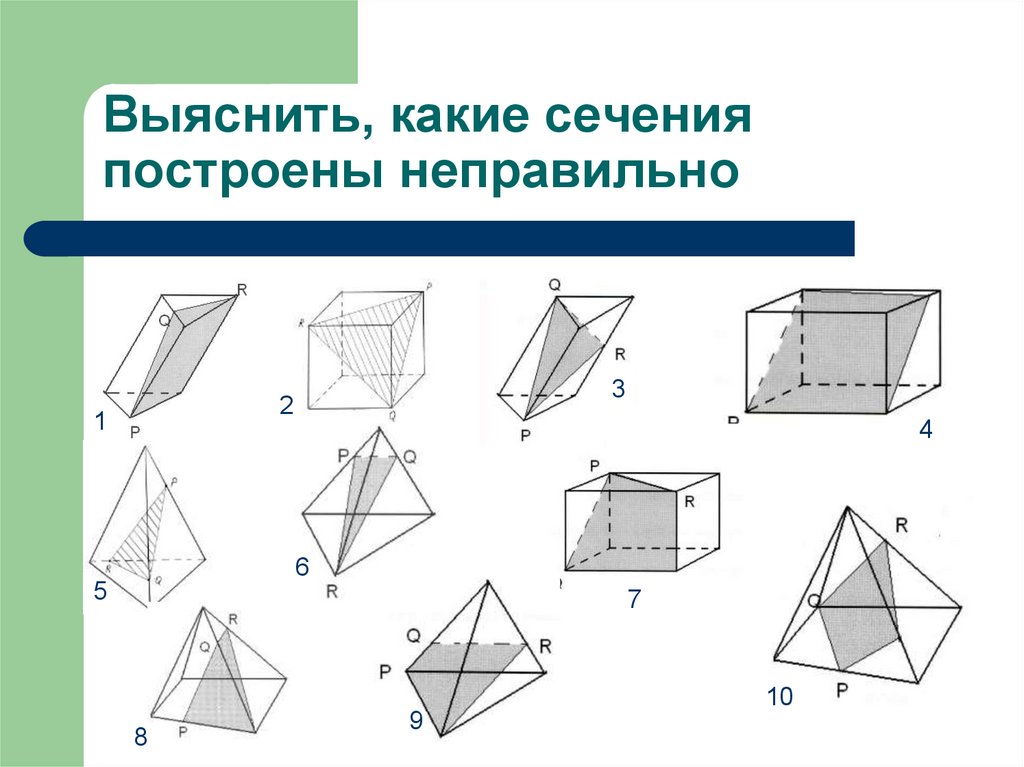
Выяснить, какие сеченияпостроены неправильно
3
2
1
4
6
5
7
10
8
9
35. Если две точки прямой лежат в плоскости, то
Домашнее заданиеПридумайте задание для
построения сечений
тетраэдра и
параллелепипеда и
постройте эти сечения.
















 Математика
Математика








