Похожие презентации:
Тепломассообмен. Дифференциальное уравнение теплопроводности. (Лекция 2)
1.
Белорусский национальный технический университетКафедра ЮНЕСКО “Энергосбережение и
возобновляемые источники энергии”
ТЕПЛОМАССООБМЕН
Лекция 2.
Дифференциальное уравнение
теплопроводности.
Г.И.Пальчёнок
2. Тепломассообмен Лекция 2
ФЕНОМЕНОЛОГИЧЕСКИЙМЕТОД
Тепломассообмен
Лекция
2
В основу исследования процессов тепло- и массообмена
положен феноменологический метод, в соответствии с
которым вещество рассматривается как сплошная среда, а
его молекулярное строение игнорируется.
Данный метод позволяет теоретически установить
общие связи (законы, закономерности) между параметрами,
характеризующими данное явление в целом. Для этого
используются общие физические законы (з-ны сохранения
энергии, массы, количества движения)
Роль конкретной физической среды при этом учитывается
эмпирическими законами Фурье, Ньютона, Фика,
включающими коэффициенты, которые определяются
экспериментально (к-ты теплопроводности λ, диффузии D,
вязкости μ) для каждой среды. (Как достоинство, так и
недостаток метода)
3. Тепломассообмен Лекция 2
СТАТИСТИЧЕСКИЙ МЕТОДНаряду с феноменологическим методом для
исследования явлений природы вообще и тепломассообмена
в частности используется статистический метод, в
котором общие законы выводятся на основании анализа
известных свойств микроскопической структуры среды без
проведения дополнительных экспериментов (достоинство).
Недостатки:
o сложность, возможность получения конечных расчётных
соотношений лишь для упрощённых физических моделей
вещества;
o свойства микроструктуры среды – предмет исследований в
специальных разделах физики, т.е. в любом случае не
обойтись без дорогостоящих экспериментов.
4. Тепломассообмен Лекция 2
Тепломассообмен модель сплошнойЛекция 2
Математическая
среды
Теоретическое исследование процессов
тепломассообмена производится на основе их
математического описания в рамках модели сплошной
среды.
Согласно этой модели в бесконечно малом
(элементарном) объёме среды ΔV , размеры которого
пренебрежимо малы по сравнению с характерным
геометрическим масштабом рассматриваемой системы
(например, с диаметром трубы), содержится очень большое
количество структурных микрочастиц.
Тогда допустимо предположение о локальном (в
пределах ΔV ) термодинамическом равновесии в любой
точке среды в любой момент времени. При этом параметры
состояния среды (Т, р, w, ρ, Сi) можно рассматривать как
непрерывные функции координат и времени.
5. Тепломассообмен Лекция 2
Состояние сплошной среды можно считатьполностью определённым, если известны значения
этих параметров (Т, р, w, ρ, Сi) в любой точке в
любой момент.
Значит целью теоретического исследования
процесса тепломассообмена является нахождение
из математического описания (модели) полей
температуры, давления, скорости, плотности и
концентраций.
При известных полях данных параметров
нетрудно рассчитать потоки теплоты, массы и
гидравлические сопротивления в рассматриваемой
системе, представляющие практический интерес.
6. Тепломассообмен Лекция 2
ТЕМПЕРАТУРНОЕ ПОЛЕПроцесс теплопроводности связан с изменением
распределения температуры тела/системы тел во времени и
пространстве.
Совокупность значений температуры во всех точках
исследуемой системы для каждого момента времени –
температурное поле. Математически температурное поле
описывается уравнением
t = f (x, y, z, τ).
Данное уравнение описывает общий случай – нестационарное
трехмерное температурное поле, изменяющееся во времени и по
всем 3-м координатам в прямоугольной (декартовой) системе.
Цель исследования теплопроводности – нахождение
температурного поля, и, следовательно, потоков теплоты (по
закону Фурье).
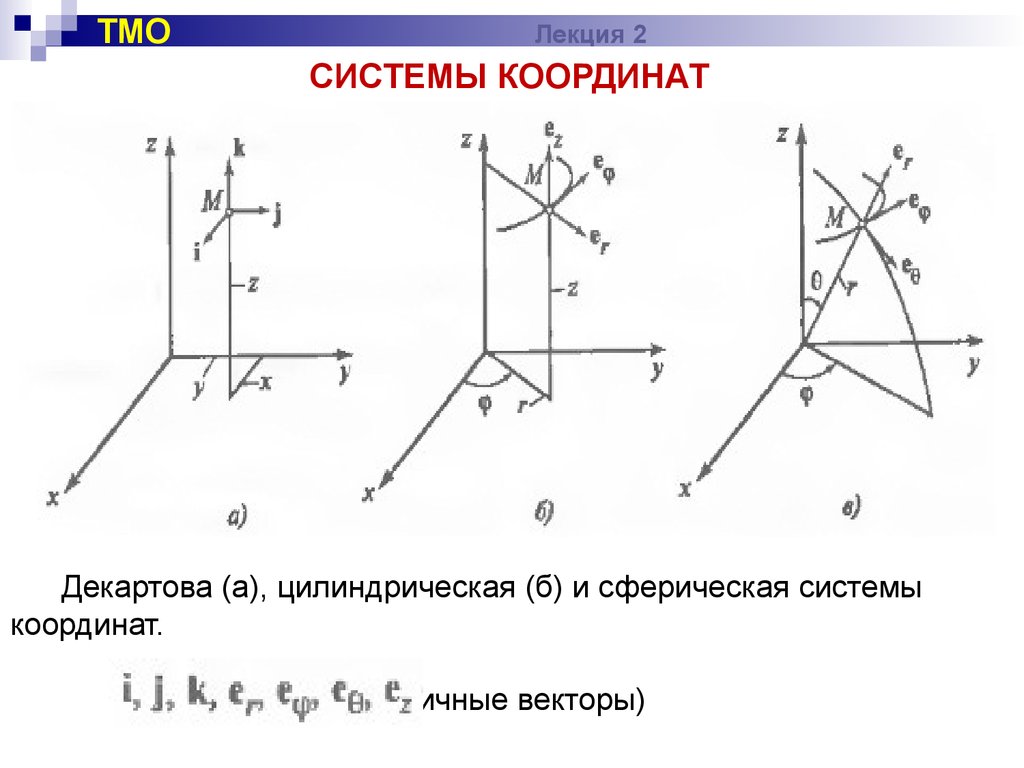
7. ТМО Лекция 2
СИСТЕМЫ КООРДИНАТДекартова (а), цилиндрическая (б) и сферическая системы
координат.
– орты (единичные векторы)
8.
Безградиентноенестационарное
температурное поле
ТП
Лекция 2
(температура одинакова по объёму тела, например, при λ ∞)
¶t ¶t ¶t
t = f (t ) ;
=
=
= 0 Þ Ñt = grad t = 0.
¶x ¶y ¶z
r ¶ r ¶ r ¶
– векторный нáбла-оператор
Ñ=i
+ j +k
¶x
¶y
¶z (оператор Гамильтона)
r ¶t
Ñt = i
+
¶x
r ¶t r ¶t
температуры
в
j –+ градиент
k
= grad
t
¶y декартовых
¶z
координатах (скалярное
произведение вектора на скаляр = вектор)
Плотность теплового потока в декартовых координатах (вектор)
¶t r
¶t r
¶t r
r
q = - l Ñt = - l i - l
j -l k
¶x
¶y
¶z
r r r
= qx + q y + qz
9.
ТМОЛекция 2
Стационарное температурное поле соответствует
установившемуся тепловому режиму теплопроводности, при
котором в каждой точке пространства температура неизменна
во времени
¶t
t = f ( x, y , z ) ;
=0
¶t
– трёхмерное стационарное
поле (3D)
¶t ¶t
t = f 2 ( x, y ) ;
=
=0
¶t ¶z
– двумерное стационарное поле
(2D)
¶t ¶t ¶t
t = f1 ( x ) ;
=
=
=0
¶t ¶y ¶z
– одномерное стационарное
поле – простейший случай
(1D)
10.
Температурноеполе аналитически находится
решения
Тепломассообмен
Лекция путём
2
дифференциального уравнения теплопроводности – уравнения
сохранения энергии в бесконечно малом (элементарном) объёме
dV, выделенном в рассматриваемом теле (среде), за бесконечно
малое (элементарное) время dt .
dV -куб с размерами
dV = dx × dy × dz ,м .
dx
, dy
, dz
3
Изменение внутренней
энергии (или энтальпии) вещества, содержащегося в dV, за время
dt равно сумме количеств теплоты:
dQ1 – поступившего извне в dV теплопроводностью и
dQ2 – выделившегося в dV за счёт внутренних источников.
11.
Допущения,принятые в модели:
Тепломассообмен
Лекция 2
o тело (среда) однородно и изотропно (свойства не зависят от
координат)
o физические свойства тела постоянны
o деформация dV из-за изменения температуры
пренебрежимо мала
o внутренние источники теплоты распределены в теле
равномерно и имеют неизменную во времени удельную
мощность qv, Вт/м3.
Количество подведённой теплоты =
dQ = dQ1 + dQ2
= изменению внутренней энергии вещества в эл. объёме
¶t
dQ = dU = cv r
dVdt
¶t
или изменению энтальпии dQ = dH = c r ¶t dVdt
p
¶t
( v = const )
( p = const )
12.
Количествотеплоты, подведённое теплопроводностью
вдоль 0х
Тепломассообмен
Лекция 2
r
¶
q
r r
dQ1x = dQx - dQx + dx = (qx - qx + dx )(dy dz )dt » - x dx (dy dz )dt
¶x
Здесь использовано разложение функции qx+dx в ряд Тэйлора
qx + dx
¶qx
¶ 2 qx ¶x 2
¶qx
= qx +
dx + 2
+ ... » qx +
dx
¶x
¶x 2!
¶x
Суммарное количество теплоты, подведённое к dV извне
где
r
r
r
¶
q
æ ¶qx
¶qz ö
y
dQ1 = - ç
+
+
÷ dx dy dz dt
¶y
¶z ø
è ¶x
r
r
r
r ¶qx ¶q y ¶qz
r
Ñq =
+
+
= div q = div ( -l grad t )
¶x
¶y
¶z
– дивергенция плотности теплового потока (вектор∙вектор=скаляр).
Количество теплоты, выделившееся за счёт внутренних источников
dQ2 = qv dV dt = qv (dx dy dz ) dt
13.
ДифференциальноеТепломассообмен уравнение теплопроводности
Лекция 2
(v = const)
Подставляя выражения для dU, dQ1 и dQ2 и сокращая на
dx·dy·dz·dτ , получаем
[u] = Дж/м3
или
или
r
r
r
æ ¶qx ¶q y ¶qz ö
¶u
= -ç
+
+
÷ + qv
¶t
¶y
¶z ø
è ¶x
r
r
r
¶
q
æ ¶qx
¶qz ö
¶t
y
cv r
= -ç
+
+
÷ + qv
¶t
¶y
¶z ø
è ¶x
r
r
= -Ñq + qv = - div q + qv
¶t
cv r
= - div ( -l grad t ) + qv = div ( l grad t ) + qv
¶t
= l Ñ 2 t + qv
14.
Дифференциальноеуравнение
ТП
Лекция 2 теплопроводности
(p = const)
[h] = Дж/м3
или
или
r
r
r
æ ¶qx ¶q y ¶qz ö
¶h
= -ç
+
+
÷ + qv
¶t
¶y
¶z ø
è ¶x
r
r
r
¶
q
æ ¶qx
¶t
¶qz ö
y
cpr
= -ç
+
+
+ qv
÷
¶t
¶y
¶z ø
è ¶x
¶t
r
r
cpr
= - div q + qv = -Ñq + qv
¶t
¶t
cp r
= div ( l grad t ) + qv
¶t
В левой части – нестационарный член, учитывающий
скорость изменения энергии (аккумулирования теплоты);
первый член справа – подвод теплоты теплопроводностью;
второй справа – внутреннее выделение теплоты.
15.
ДИФФЕРЕНЦИАЛЬНОЕТепломассообмен УРАВНЕНИЕ ТЕПЛОПРОВОДНОСТИ
Лекция 2
(общий вид)
Опуская индекс при удельной теплоёмкости, указывающий на
характер процесса, получаем дифференциальное уравнение
теплопроводности в общем виде, связывающее временные и
пространственные изменения температуры в любой точке тела, в
котором осуществляется процесс теплопроводности
é¶ æ
¶t
¶t ö ¶ æ
¶t ö ¶ æ
¶t ö ù
cr
= - ê ç -l ÷ + ç -l ÷ + ç -l ÷ú + qv
¶t
¶x ø ¶y è
¶y ø ¶z è
¶z ø û
ë ¶x è
где физические свойства вещества (с, λ, r ) – функции координат и
времени.
При постоянных физических свойствах вещества (с, λ, r )
¶t
l æ ¶ 2t ¶ 2t ¶ 2 t ö qv
=
+ 2 + 2 ÷+
ç
2
¶t c r è ¶x
¶y
¶z ø c r
¶t
q
= aÑ 2t + v
¶t
cr
16.
Коэффициенттемпературопроводности
(диффузии
теплоты)
Тепломассообмен
Лекция
2
l
м2
a=
,
cр r
с
физический параметр вещества. Важная характеристика скорости
изменения температуры в нестационарных тепловых процессах.
Если коэффициент теплопроводности λ – характеристика
способности тела проводить теплоту, то а – мера тепловой
инерции тела/вещества (скорость изменения температуры тем
выше, чем выше а, т.е. чем выше λ и ниже ср и ρ).
Скалярный оператор Лапласа в декартовой системе координат
¶
¶
¶
Ñ º Ñ ×Ñ º D = 2 + 2 + 2
¶x
¶y
¶z
2
2
2
2
17. Тепломассообмен Лекция 2
Частныеслучаи уравнения теплопроводности
Тепломассообмен
Лекция 2
¶t
qv
2
= aÑ t +
¶t
cr
Уравнение Фурье – отсутствуют внутренние источники теплоты, qv = 0
¶t
= aÑ 2t
¶t
Уравнение Пуассона – стационарная задача
¶t
qv
2
= 0; aÑ t +
=0
¶t
cr
Уравнение Лапласа – стационарная задача, внутренние источники
отсутствуют, qv = 0
¶t
= qv = 0; Ñ 2t = 0
¶t
18. Тепломассообмен Лекция 2
Жан БатистЖозеф Фурье (Jean Baptiste Joseph Fourier;
21 2марта 1768 — 16 мая
Тепломассообмен
Лекция
1830), французский математик и физик.
Уравнение Фурье
¶t
= aÑ 2t
¶t
Родился в семье портного. В 9 лет потерял
обоих родителей. Сироту устроили в Военную
школу при бенедиктинском монастыре.
В 1808 г. получает от Наполеона титул барона и
награждается орденом Почётного легиона. В
1812 г. Фурье получает Большую премию
Академии за аналитическую теорию
теплопроводности, несмотря на нестрогие
доказательства. Впрочем, полная строгость
была достигнута только в эпоху Гильберта.
Свои методы (ряды и интегралы Фурье) он
использовал в теории распространения тепла.
Но вскоре они стали исключительно мощным
инструментом математического исследования
самых разных задач — особенно там, где есть
волны и колебания. А этот круг чрезвычайно
широк — астрономия, акустика, теория
приливов, радиотехника и др.
19. Тепломассообмен Лекция 2
СимеоонТепломассообменДенио Пуассоон (Siméon Denis Poisson, 21 июня
1781–25
апреля 1840) —
Лекция
2
знаменитый французский физик и математик.
Отец его, солдат ганноверских войск, дезертировавший вследствие притеснений
офицера, занимал незначительную административную должность.
При Наполеоне он возведён в бароны, а при Луи-Филиппе был сделан пэром
Франции.
Число учёных трудов Пуассона превосходит 300. Они относятся к разным областям
чистой математики, математической физики, теоретической и небесной механики.
Уравнение Пуассона
qv
aÑ t +
=0
cr
2
20. Тепломассообмен Лекция 2
Пьер-Симо1749
о н Лаплаос (фр. Pierre-Simon Laplace; 23 марта
Тепломассообмен
Лекция
2 — 5 марта 1827) —
выдающийся французский математик, физик и астроном. Родился в местечке
Бомон-ан-Ож (Нормандия) в семье небогатого крестьянина; впоследствии граф и
маркиз, Лаплас стыдился своего незнатного происхождения. Известен работами в
области небесной механики, дифференциальных уравнений, один из создателей
теории вероятностей. Заслуги Лапласа в области чистой и прикладной математики
и особенно в астрономии громадны: он усовершенствовал почти все отделы этих
наук.
Уравнение Лапласа
Ñ 2t = 0
21.
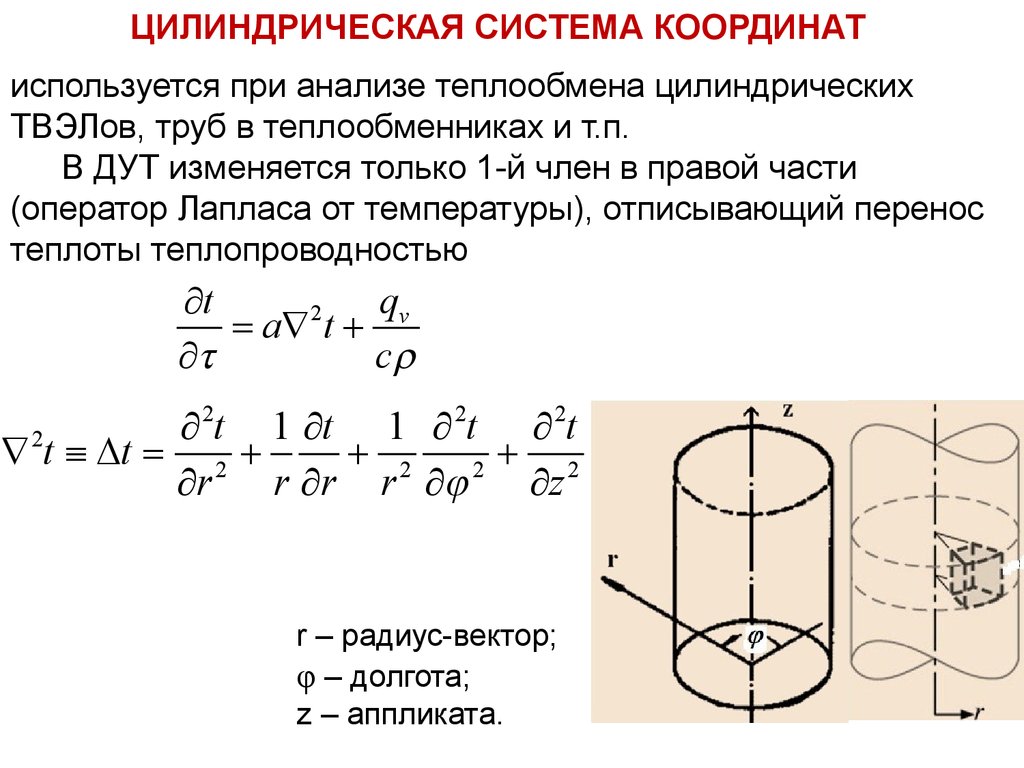
ЦИЛИНДРИЧЕСКАЯ СИСТЕМАЛекцияКООРДИНАТ
Тепломассообмен
2
используется при анализе теплообмена цилиндрических
ТВЭЛов, труб в теплообменниках и т.п.
В ДУТ изменяется только 1-й член в правой части
(оператор Лапласа от температуры), отписывающий перенос
теплоты теплопроводностью
¶t
qv
2
= aÑ t +
¶t
cr
2
2
2
¶
t
1
¶
t
1
¶
t
¶
t
2
Ñ t º Dt = 2 +
+ 2
+ 2
2
¶r
r ¶r r ¶j
¶z
r – радиус-вектор;
φ – долгота;
z – аппликата.
22.
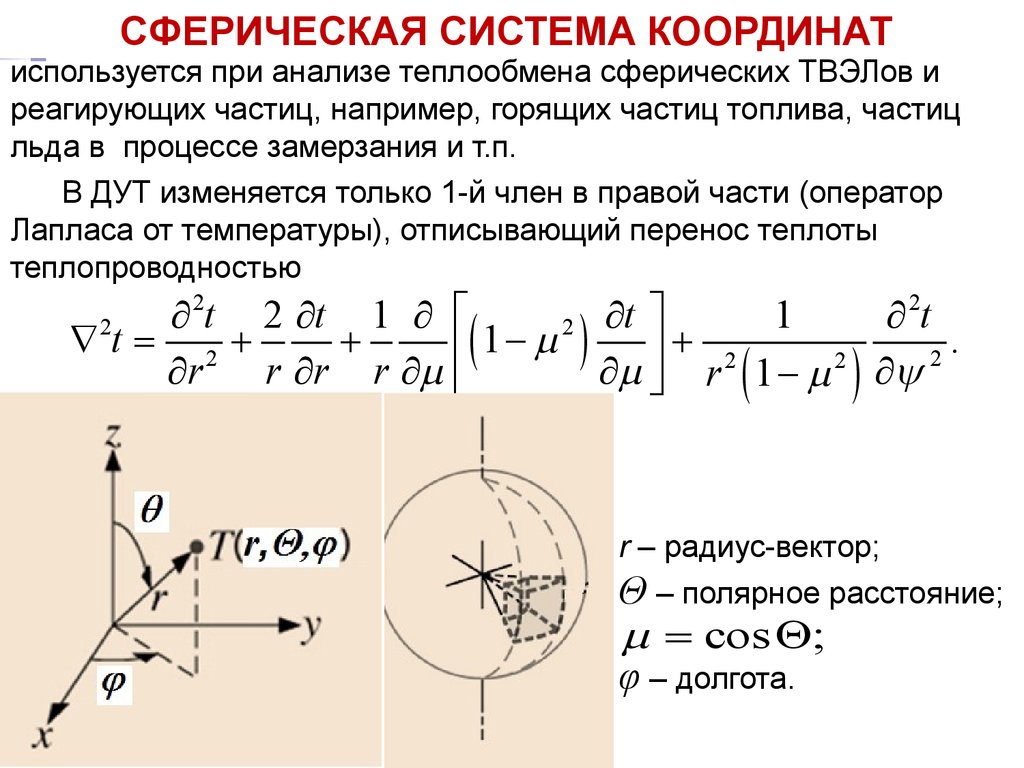
Тепломассообмен2
СФЕРИЧЕСКАЯ СИСТЕМАЛекция
КООРДИНАТ
используется при анализе теплообмена сферических ТВЭЛов и
реагирующих частиц, например, горящих частиц топлива, частиц
льда в процессе замерзания и т.п.
В ДУТ изменяется только 1-й член в правой части (оператор
Лапласа от температуры), отписывающий перенос теплоты
теплопроводностью
2
2
é
ù
¶
t
2
¶
t
1
¶
¶
t
1
¶
t
2
2
Ñt= 2+
+
1- m )
+ 2
.
(
2
ê
ú
2
¶r
r ¶r r ¶m ë
¶m û r ( 1 - m ) ¶y
r – радиус-вектор;
Θ – полярное расстояние;
m = cos Q;
φ – долгота.



















 Философия
Философия








