Определения прямых и углов

1. Определения прямых и углов

• 1.прямые на плоскости называются параллельными,
если они имеют одну общую точку(а в).
с
• 2.прямая, пересекающая две прямые
одновременно, называется секущей.
3.два отрезка называются
параллельными, если они лежат на
параллельных прямых.
АВ СД, если а в, при этом
а
АВ € а, СД € в.
в
а
в
А
.
В
.
.
С
.
Д

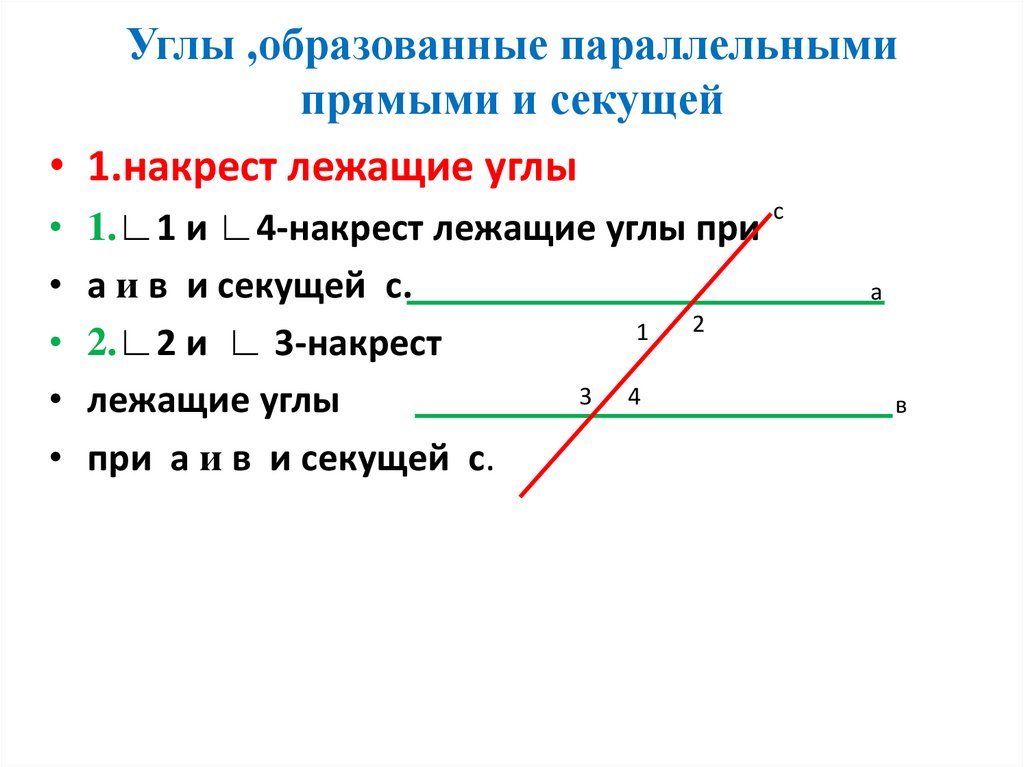
2. Углы ,образованные параллельными прямыми и секущей

• 1.накрест лежащие углы
1.∟1 и ∟4-накрест лежащие углы при
а и в и секущей с.
2
1
2.∟2 и ∟ 3-накрест
3 4
лежащие углы
при а и в и секущей с.
с
а
в

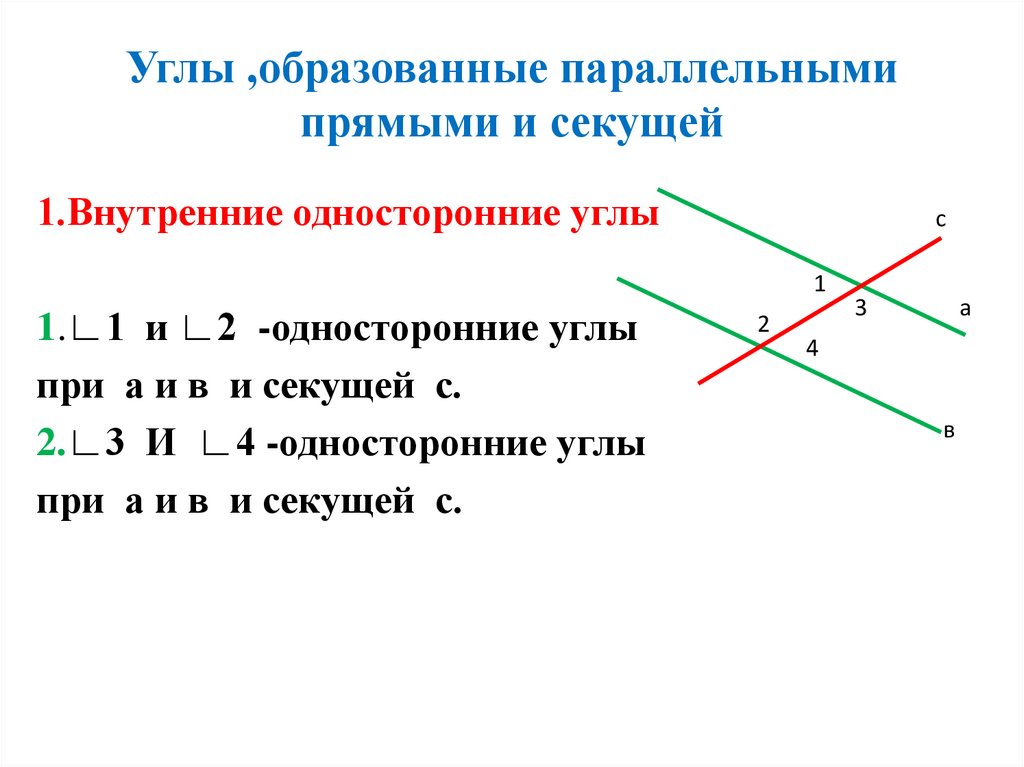
3. Углы ,образованные параллельными прямыми и секущей

1.Внутренние односторонние углы
с
1
1.∟1 и ∟2 -односторонние углы
при а и в и секущей с.
2.∟3 И ∟4 -односторонние углы
при а и в и секущей с.
2
3
а
4
в

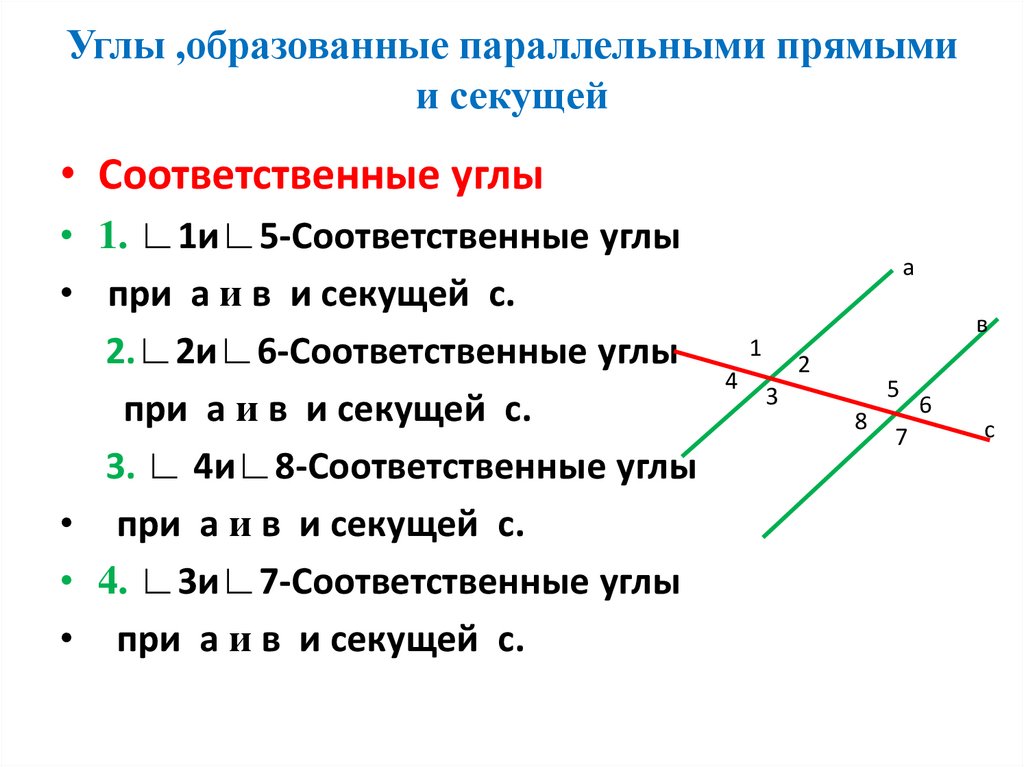
4. Углы ,образованные параллельными прямыми и секущей

• Соответственные углы
• 1. ∟1и∟5-Соответственные углы
• при а и в и секущей с.
2.∟2и∟6-Соответственные углы
при а и в и секущей с.
3. ∟ 4и∟8-Соответственные углы
• при а и в и секущей с.
• 4. ∟3и∟7-Соответственные углы
• при а и в и секущей с.
а
в
1
4
2
3
5
8
7
6
с

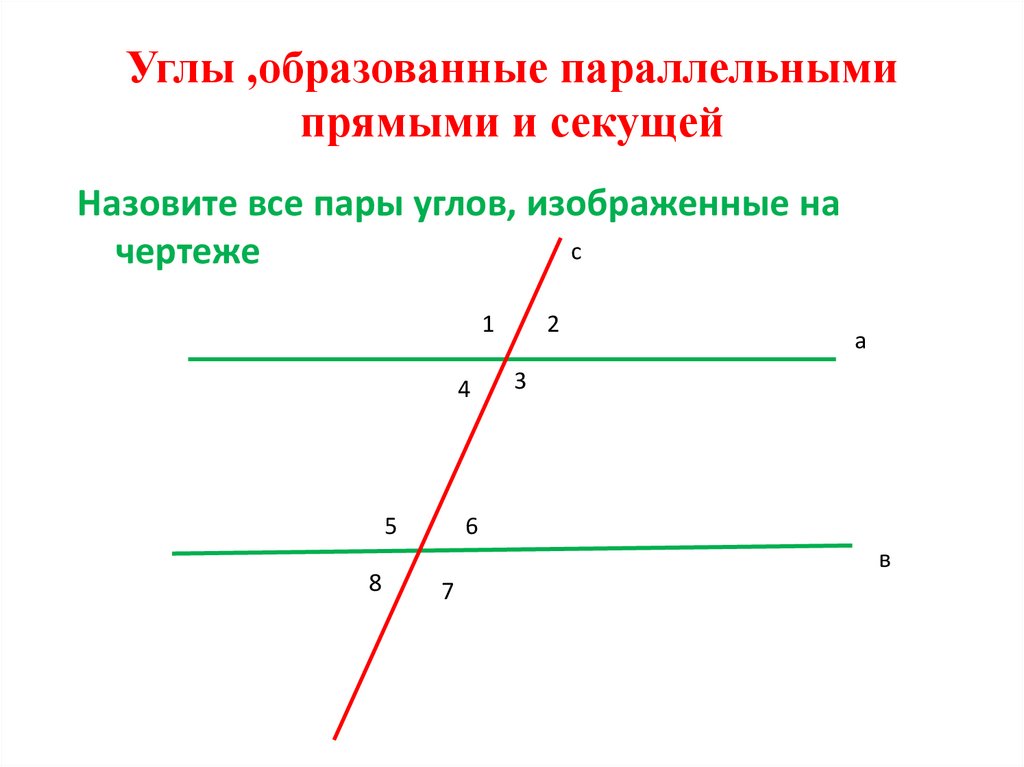
5. Углы ,образованные параллельными прямыми и секущей

Назовите все пары углов, изображенные на
с
чертеже
1
4
5
8
2
а
3
6
в
7

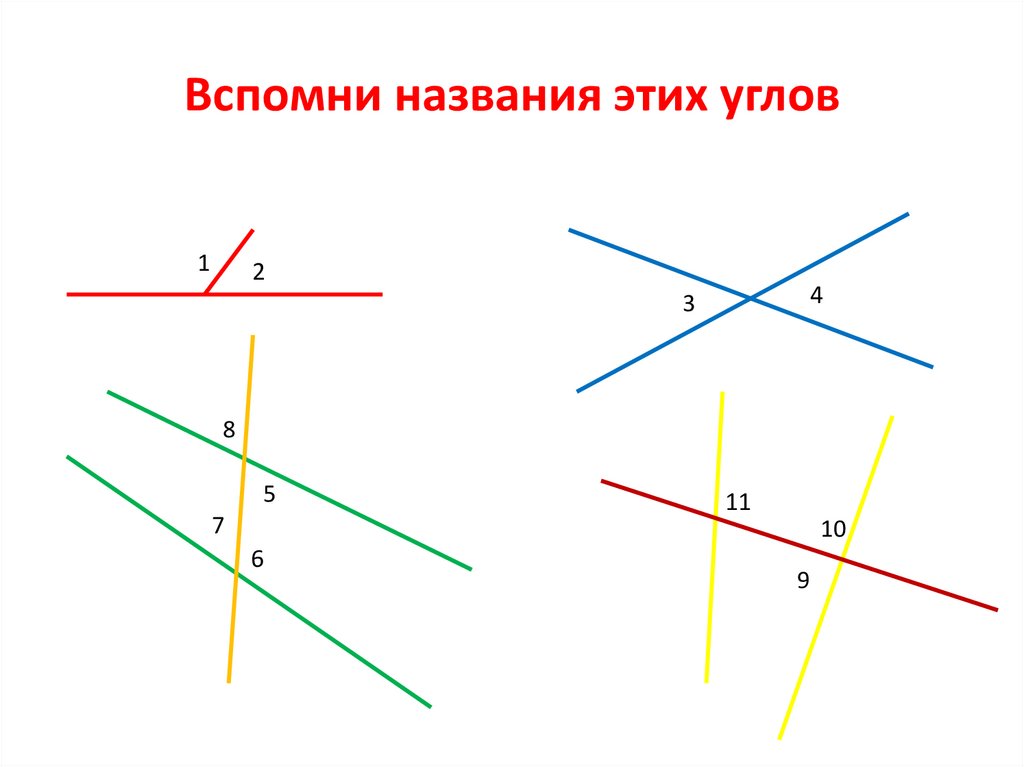
6. Вспомни названия этих углов

1
2
4
3
8
5
7
11
10
6
9

7. Правильно или нет

1 2
4 3
5
6
7 8
˪1 и ˪2-вертикальные
˪5 и ˪8-смежные
˪4 и ˪6-соответственные
˪3 и ˪5-накрест лежащие
˪2 и ˪5 –внутренние односторонние
˪6 и ˪2- внутренние односторонние
˪5 и ˪8-вертикальные
А как правильно?

8. Найди углы на чертеже

Углы :1и2-вертикальные
6и2-накрест лежащие
6и8-смежные
5и8-накрест лежащие
5и7-вертикальные
4и6-вертикальные
3и4-смежные
3и8-вертикальные
1и7-смежные

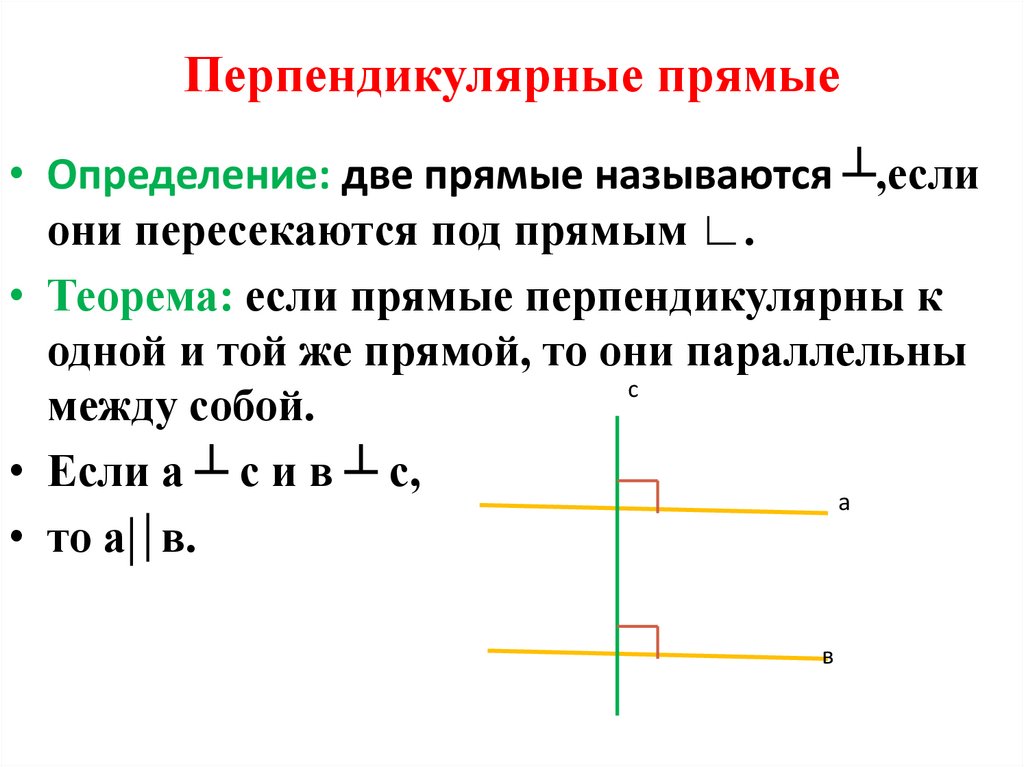
9. Перпендикулярные прямые

• Определение: две прямые называются ┴,если
они пересекаются под прямым ∟.
• Теорема: если прямые перпендикулярны к
одной и той же прямой, то они параллельны
с
между собой.
• Если а ┴ с и в ┴ с,
а
• то а в.
в

10. Решение задач

с
а
х
60
в
3
• Найди углы 1,2,3,4,5,6,
• Если ∟х=60,∟у=100
6
100 4
у
5
1
2

11. Найди углы

Дано: а в, с-секущая,
а ┴ с, ∟1=90
Найти: все
остальные углы.
в
а
1
4
8 5
6
7
3
2
с

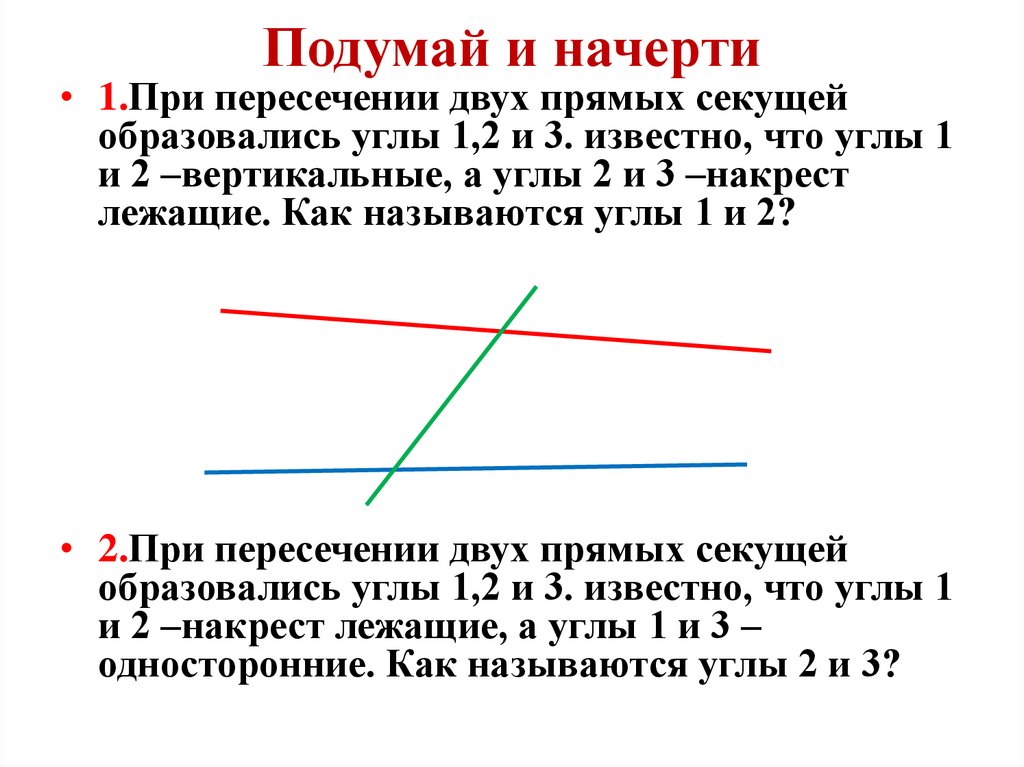
12. Подумай и начерти

• 1.При пересечении двух прямых секущей
образовались углы 1,2 и 3. известно, что углы 1
и 2 –вертикальные, а углы 2 и 3 –накрест
лежащие. Как называются углы 1 и 2?
• 2.При пересечении двух прямых секущей
образовались углы 1,2 и 3. известно, что углы 1
и 2 –накрест лежащие, а углы 1 и 3 –
односторонние. Как называются углы 2 и 3?

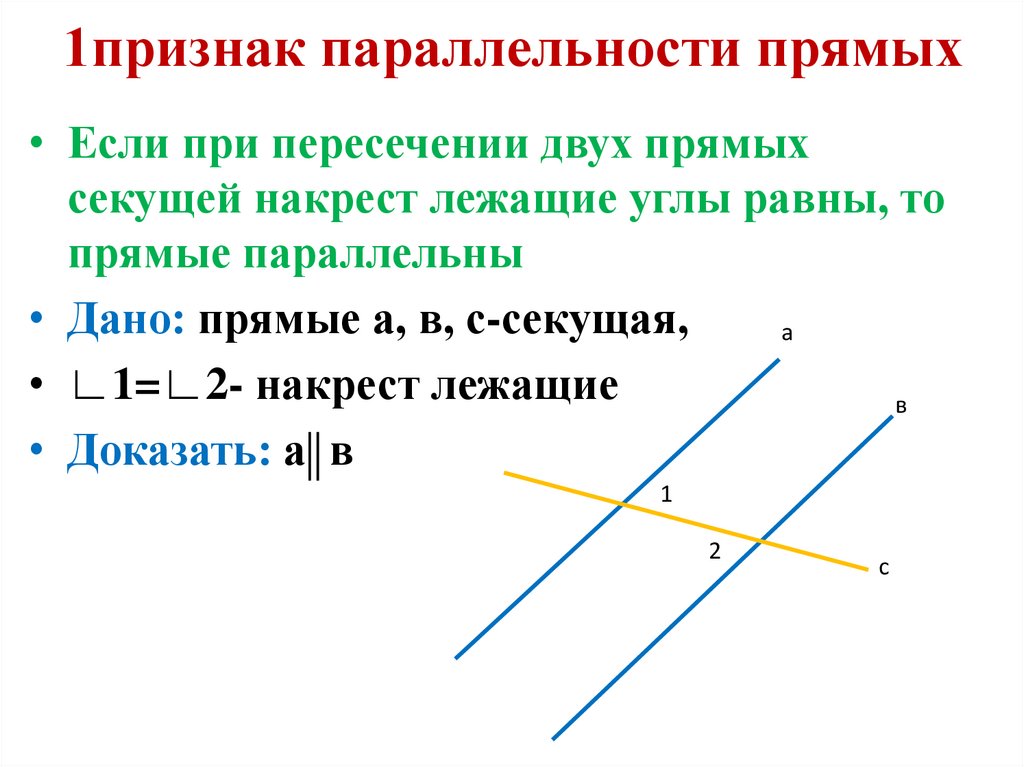
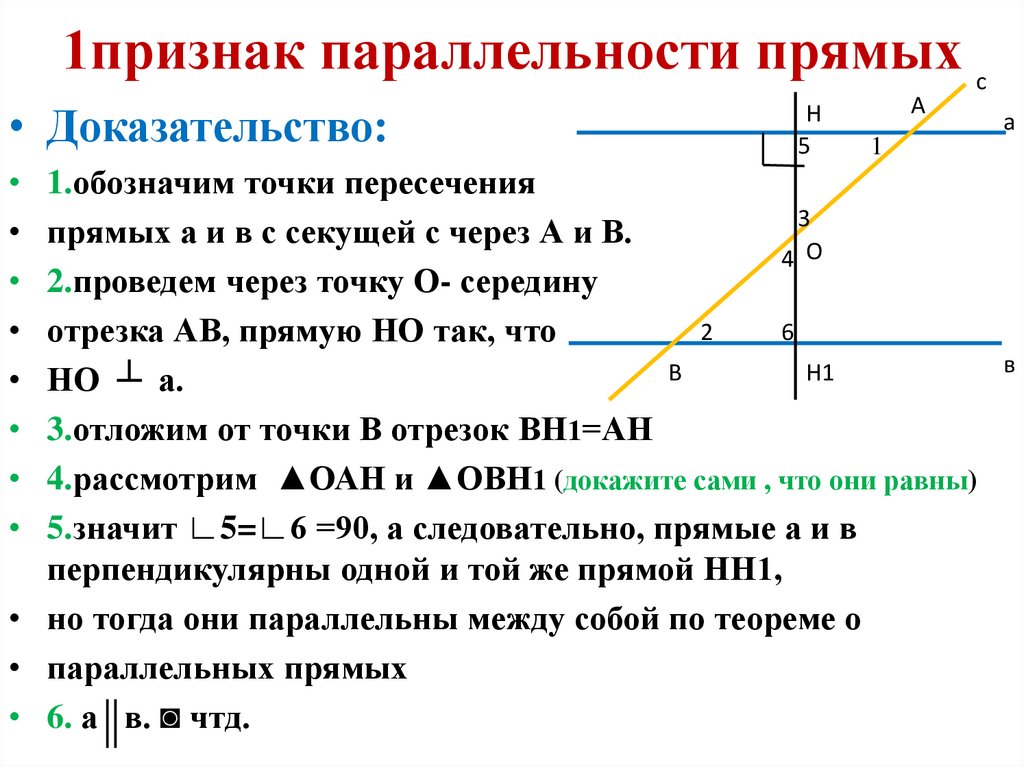
13. 1признак параллельности прямых

• Если при пересечении двух прямых
секущей накрест лежащие углы равны, то
прямые параллельны
• Дано: прямые а, в, с-секущая,
а
• ∟1=∟2- накрест лежащие
в
• Доказать: а в
1
2
с

14. 1признак параллельности прямых

с
• Доказательство:
Н
5
А
а
1
1.обозначим точки пересечения
3
прямых а и в с секущей с через А и В.
4 О
2.проведем через точку О- середину
2
6
отрезка АВ, прямую НО так, что
В
Н1
НО ┴ а.
3.отложим от точки В отрезок ВН1=АН
4.рассмотрим ▲ОАН и ▲ОВН1 (докажите сами , что они равны)
5.значит ∟5=∟6 =90, а следовательно, прямые а и в
перпендикулярны одной и той же прямой НН1,
• но тогда они параллельны между собой по теореме о
• параллельных прямых
• 6. а в. ◙ чтд.
в

15. 2 признак параллельности прямых

• Если при пересечении двух прямых
секущей соответственные углы равны, то
прямые параллельны
с
1
а
• Дано: прямые а, в, с-секущая,
3
• ∟1=∟2- соответственные.
2
в
• Доказать: а в
• Доказательство:
• 1.∟1= ∟3(вертикальные) и ∟1=∟2(по
условию) → ∟2=∟3.
• 2.∟2=∟3 являются накрест лежащими →
• а в по первому признаку параллельности
прямых. ◙ чтд.

16. 3 признак параллельности прямых

• Если при пересечении двух прямых
секущей сумма односторонних углов
с
равна 180 , то прямые параллельны
а
1
2
• Если ∟1+∟2=180, то а в.
в

17. Проверяем домашнее задание

с
№186(3)
1 2
а
4 3
Дано: по чертежу
8 5
∟1=45,∟7 в 3раза больше ,
в
7 6
чем ∟3
Доказать: а в
Доказательство:
∟1=∟3=45(вертикальные);
∟7=∟5=45*3=135( ?);
∟3+∟5=45+135=180(односторонние) а в
(по 3 признаку)

18. Вставь пропущенные слова и назови признак

• Если при пересечении двух прямых
секущей ____?_____ лежащие углы равны,
• то прямые параллельны
• Если при пересечении двух прямых
секущей соответственные углы равны, то
прямые _____?______
• Если при пересечении двух прямых
секущей _____?____ односторонних углов
равна 180 , то прямые параллельны

19. Прочитай-подумай-скажи

• 1.При пересечении двух прямых секущей
образовались углы 1,2 и 3. известно, что углы 1
и 2 –накрест лежащие, а углы 2 и 3 –
вертикальные. Как называются углы 1 и 3?
• 2.При пересечении двух прямых секущей
образовались углы 1,2 и 3. известно, что углы 1
и 2 –накрест лежащие, а углы 1 и 3 –
соответственные. Как называются углы 2 и 3?

20. Задачи по чертежам

с
Рис.1
По данным на
чертеже доказать,
что а в
а
40
140
в
с
а
1
Рис. 2
По данным на
чертеже найти
∟1 и ∟2,если а в
2
в
30

21. Задачи по чертежам

• По данным на чертеже
• Найдите угол х
30
а
х
150
60
в
с
18
• По данным на чертеже
• Докажите, что а в
а
в
х
9х

22. Вставь пропущенные слова и назови признак

• Если при пересечении двух прямых
секущей ______?______ углы равны,
• то прямые параллельны
• Если при пересечении двух прямых
секущей накрест _____?_____ углы равны,
то прямые _____?______
• Если при пересечении двух прямых
секущей _____?___ углов равна 180 , то
прямые параллельны

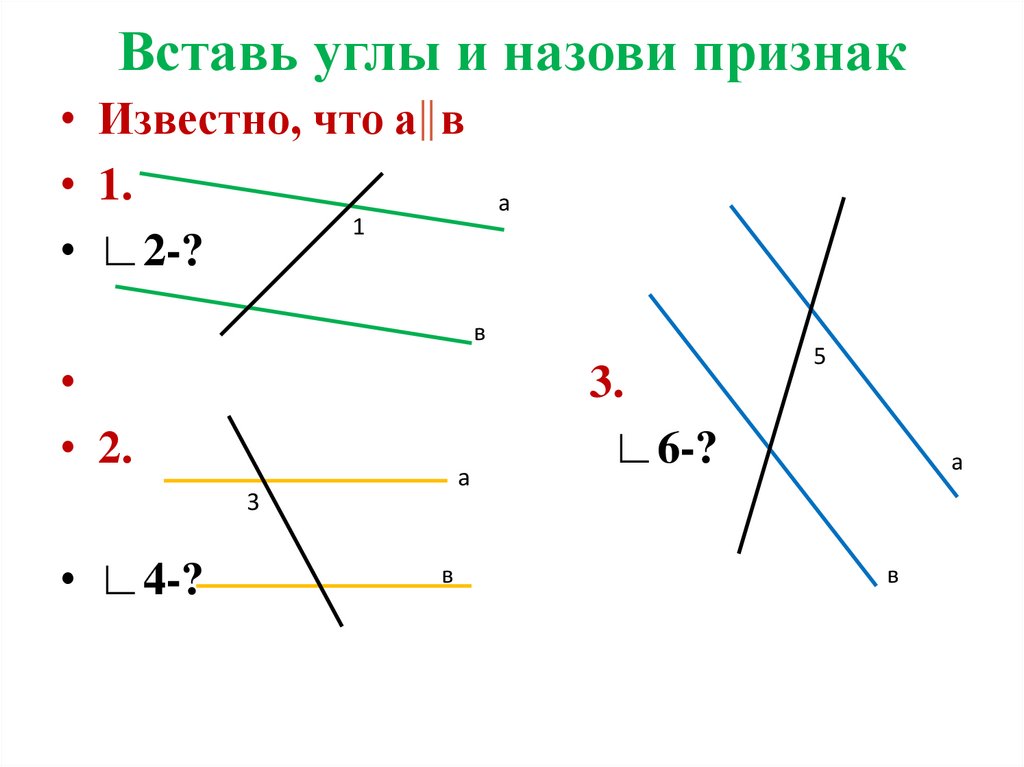
23. Вставь углы и назови признак

• Известно, что а в
• 1.
1
• ∟2-?
а
в
• 2.
а
3
• ∟4-?
в
3.
∟6-?
5
а
в

24. Назови углы и найди их величину, если а в

110
а
3
2
1
а
40
4
в
6
в
5
50
а
в

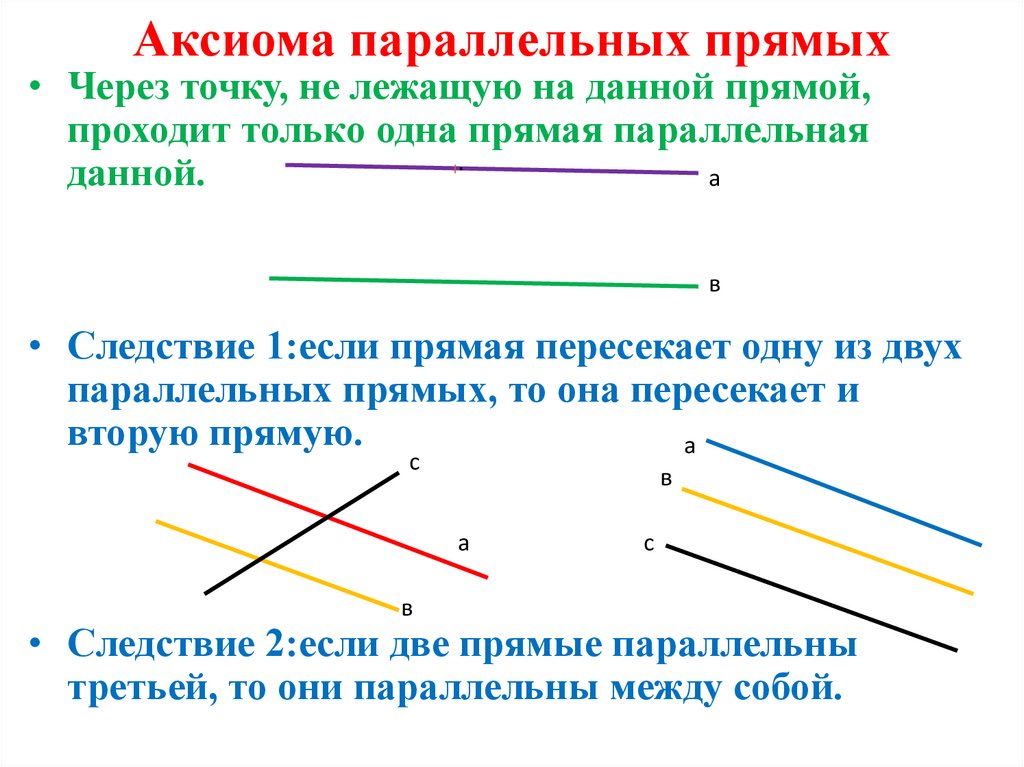
25. Аксиома параллельных прямых

• Через точку, не лежащую на данной прямой,
проходит только одна прямая параллельная
.
данной.
а
в
• Следствие 1:если прямая пересекает одну из двух
параллельных прямых, то она пересекает и
вторую прямую.
а
с
в
а
в
с
• Следствие 2:если две прямые параллельны
третьей, то они параллельны между собой.

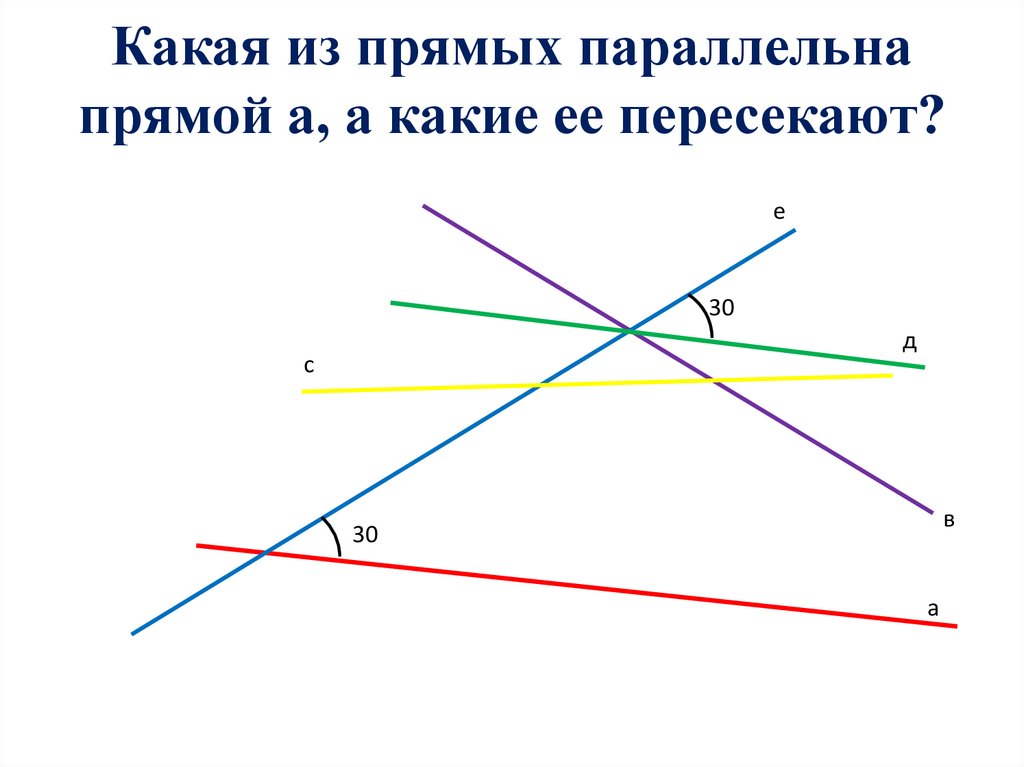
26. Какая из прямых параллельна прямой а, а какие ее пересекают?

е
30
д
с
в
30
а

27. Аксиома параллельных прямых

• Через точку, не лежащую на данной прямой,
проходит ? прямая параллельная
данной.
.
а
в
• Следствие 1:если прямая пересекает одну из двух
параллельных прямых, то она пересекает и ?
прямую.
а
с
в
а
с
в
• Следствие 2:если две прямые параллельны
третьей, то они ? между собой.

28. Найди ошибку, если а в

а
а
в
50
в
60
120
80
110

29. Если прямые параллельные прямые пересечены секущей, то

1. ? углы равны.
2. ? углы равны.
3.сумма ? равна 180.
Сделай рисунок к каждому
свойству

30. Задачи по чертежам

с
с
а
а
а
2
2.
1.
1
3.
72
1
в
в
в
А
с
2
В
А
С
5
3
2
4
О
4.
5.
1=138
Д
С
о
В

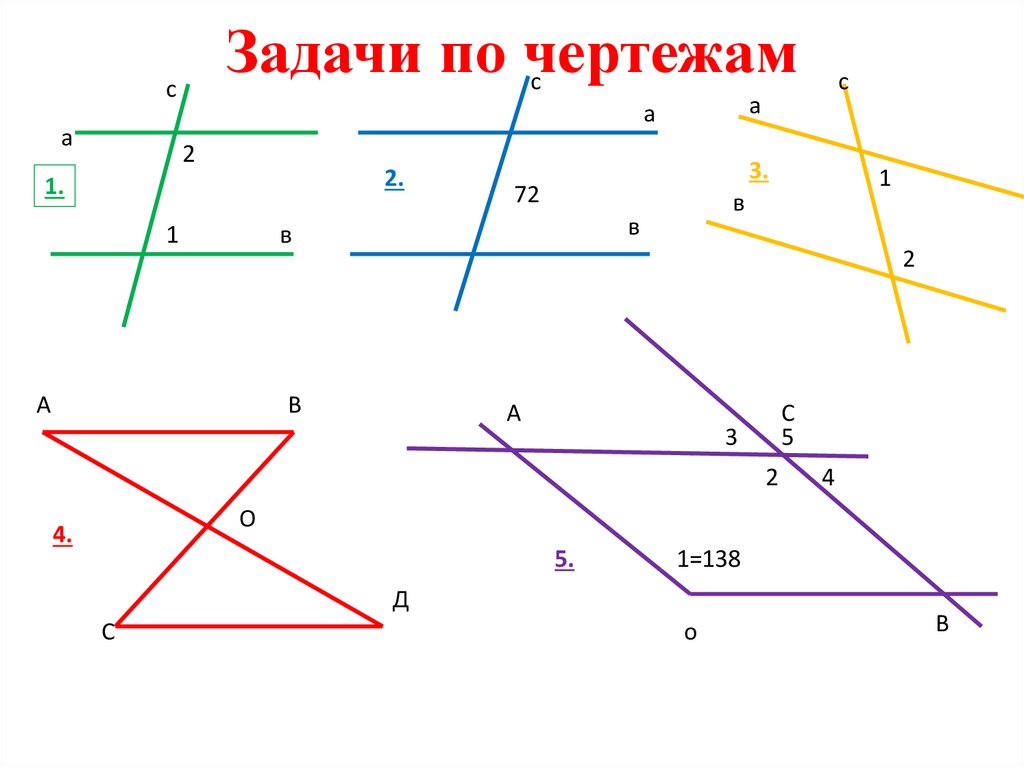
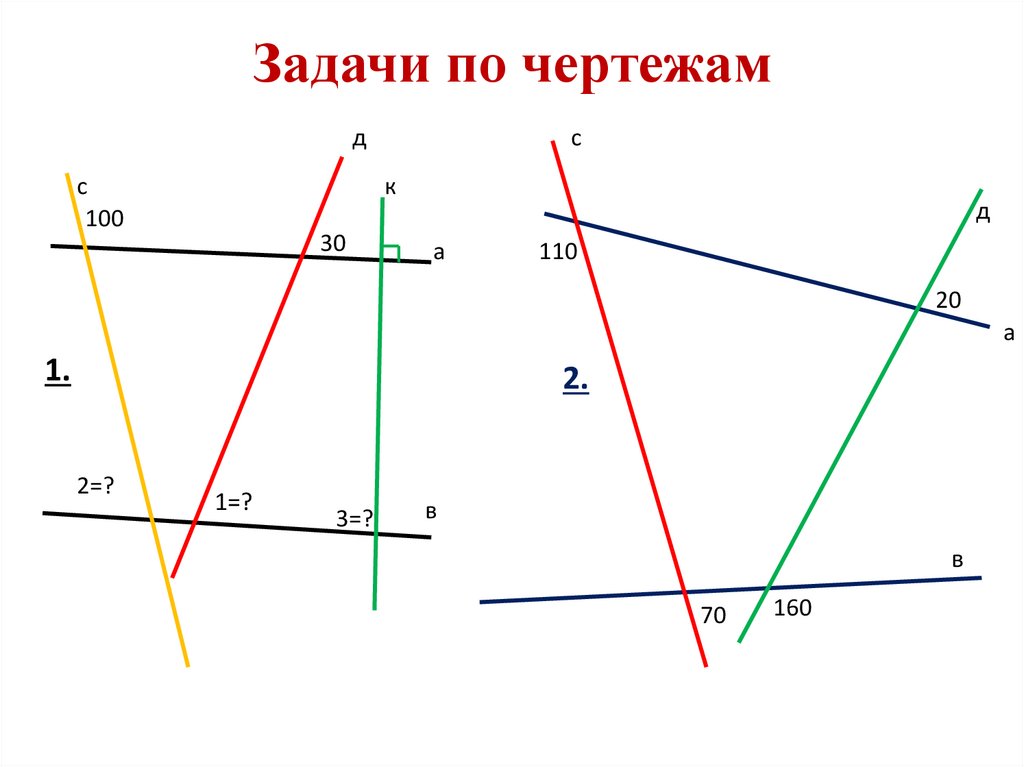
31. Задачи по чертежам

д
с
100
с
к
30
д
а
110
20
а
1.
2.
2=?
1=?
3=?
в
в
70
160

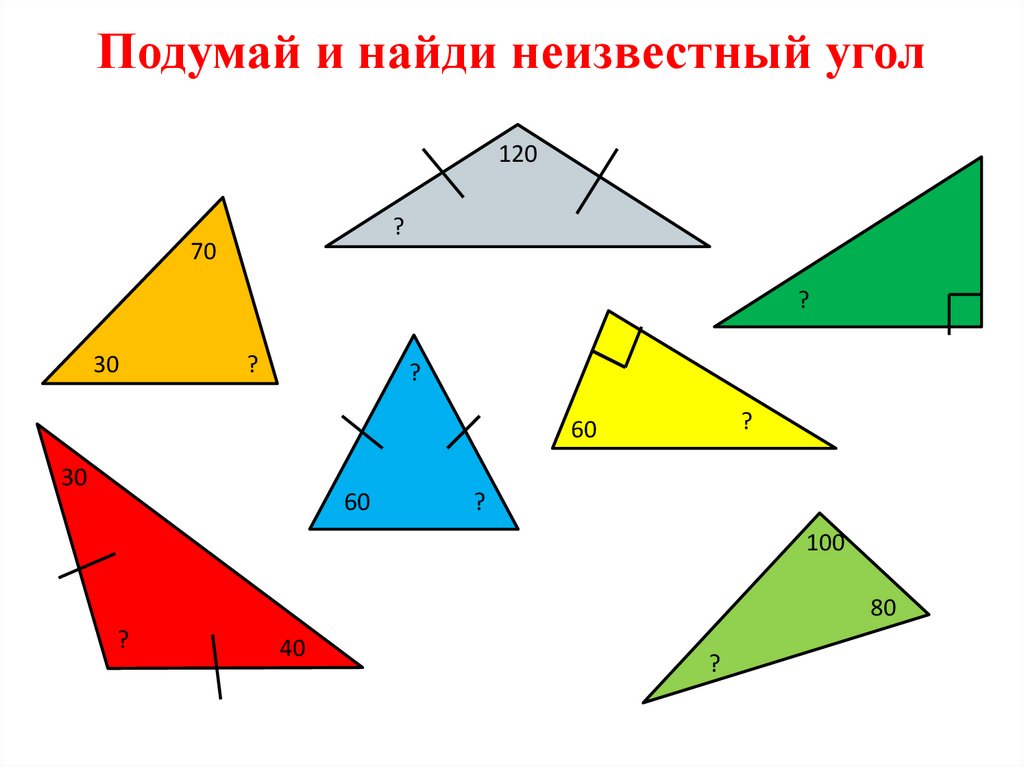
32. Подумай и найди неизвестный угол

120
?
70
?
30
?
?
?
60
30
60
?
100
80
?
40
?

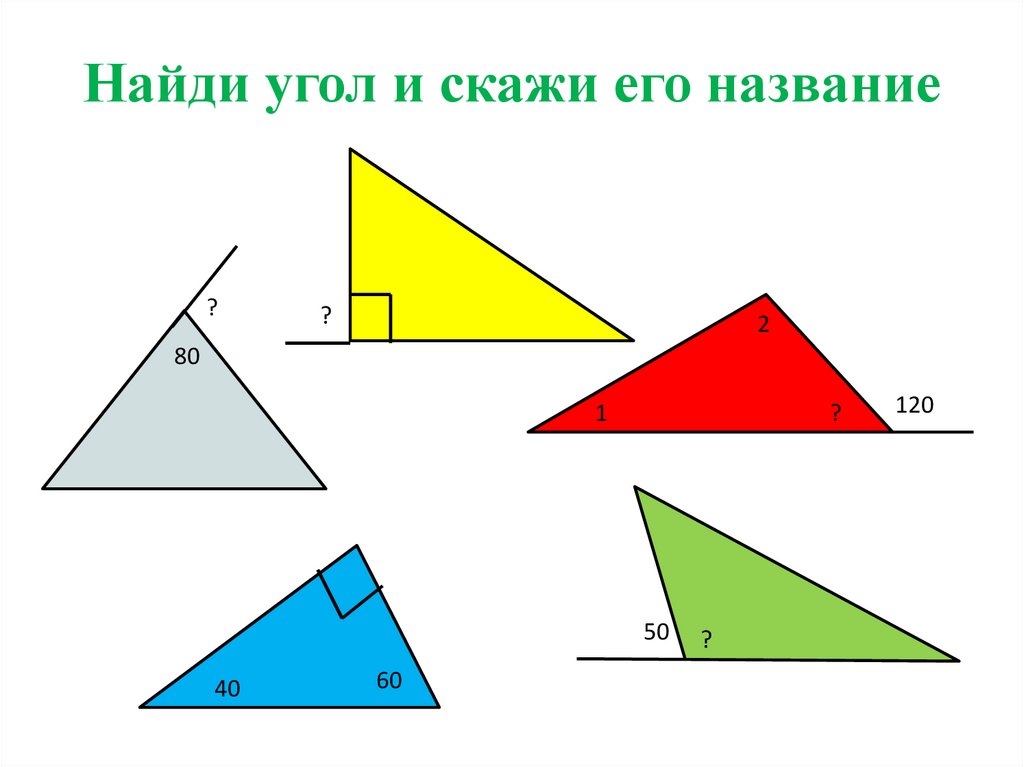
33. Найди угол и скажи его название

?
?
2
80
1
?
50
40
60
?
120

34. Теорема о соотношениях между сторонами и углами треугольника

• Теорема: в треугольнике
• 1)напротив большей стороны лежит больший
угол,
• 2)напротив большего угла лежит большая
В
сторона.
• Дано: ▲АВС;
• 1)если ∟В больше ,чем ∟А и ∟С,
• то АС больше ,чем АВ и ВС;
А
• 2)если АС больше, чем АВ и ВС,
• то ∟ В больше, чем ∟А и ∟С.
С

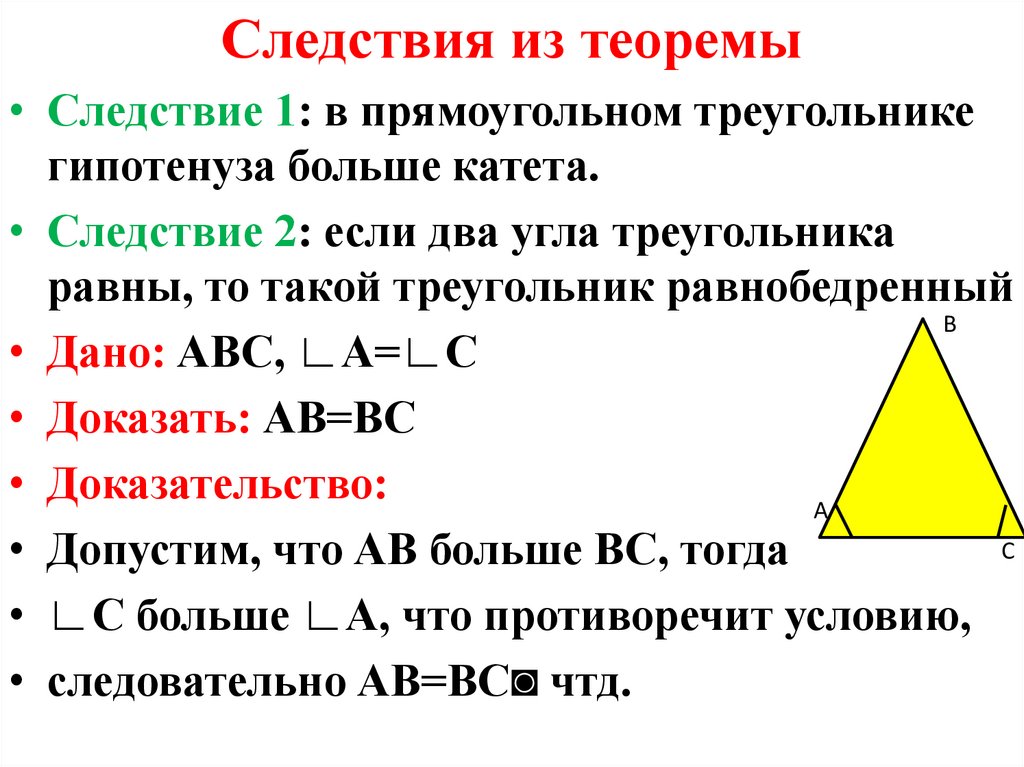
35. Следствия из теоремы

• Следствие 1: в прямоугольном треугольнике
гипотенуза больше катета.
• Следствие 2: если два угла треугольника
равны, то такой треугольник равнобедренный
В
• Дано: АВС, ∟А=∟С
• Доказать: АВ=ВС
• Доказательство:
А
С
• Допустим, что АВ больше ВС, тогда
• ∟С больше ∟А, что противоречит условию,
• следовательно АВ=ВС◙ чтд.